替代定理的几点应用探讨
简智敏 卢光宝
(1.漳州职业技术学院 机械工程及自动化系,福建 漳州 363000;2.福建工程学院,福建 福州 350118)
替代定理的几点应用探讨
简智敏1卢光宝2
(1.漳州职业技术学院 机械工程及自动化系,福建 漳州 363000;2.福建工程学院,福建 福州 350118)
替代定理是几个重要的电路定理之一。关于替代定理应用中的问题,以及是否应该加补充条件的讨论一直存在。考虑到定理是用来思考判断和推理的,从完整性和严谨性角度,作者经研究及实际教学经验,从三个方面提出替代定理应用的思路和见解:一是含控制量的二端网络的替代;二是用一个适当的电阻替代;三是灵活选择替换形式,避免改变原电路的解。
替代定理;控制量;二端网络
替代定理是几个重要的电路定理之一,既为其他电路定理提供理论支撑,也是电路分析计算的重要依据。已有从事相关教学的教师和学者对其进行了较深刻的研究。在众多文献中,对含控制量的替代、电阻替代等问题有不同表述和建议,有些表述有不尽完善或有待探讨之处。定理是用逻辑的方法判断为正确并作为推理的根据的真命题,如果要形成完整并严谨的逻辑命题,则要在叙述、推导和应用过程中加入合适的补充条件。基于替代定理在电路教学和电路分析中的重要性,叙述严谨而应用方便是最佳选择,以下是笔者对于替代定理应用的思路和见解。
一、被替代网络含控制量的情形
文献[1]关于替代定理的表述如下:“如果在NB中有NA中受控源的控制量,NB被替代后将无法表达这种控制关系,这时,NB就不可以被替代。”这容易让初学者得出这样的结论:“即含控制量的二端网络不能应用替代定理来化简”。当然深入理解这句话,就可以得出更完整的解析,NB被替代后电路如果能继续表达这种控制关系时,NB可以被替代。
那么,怎样使替代后的电路能继续表达这种控制关系呢,很多文献给出了自己的观点,总结起来就是:“被替代支路中如包含有其他支路的控制量,则替代后此控制量仍应保留而不能取消。”[1]但众多文献对控制量如何保留或者保留后使电路仍然易于分析或计算没有给出明确叙述。经过分析论证,本文给出的思路是:“被替代二端网络中如包含有其他支路的控制量,若将该控制量用被替代二端网络的端口电压或电流的线性组合来表示,则二端网络可以被替代。”下面通过例子来说明这种处理方法。
例1,如图1所示,易求得I=-4.4 A,Ix=1.4 A,U=7.2 V,则分别用I=-4.4 A的电流源或U=7.2 V的电压源来替代,Ix分别用-(3+I)或(5-0.5U)来表示,分别如图2中(a)和(b)所示。通过上面例子,可以总结为:被替代二端网络中的控制量用其端口电压或电流的线性组合来表示后,二端网络可以被替代。
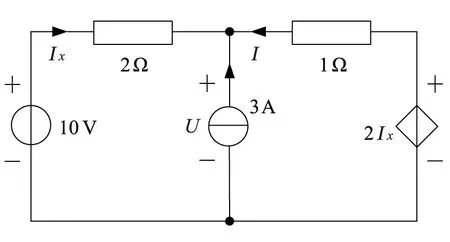
图1 例1原电路图

图2 例1被替代后的电路图
二、外电路含激励的情形
对于用阻值为RK=UK/IK的电阻替代二端网络的情况,部分教材和文献没有提及或没有给出很明确的处理方法。有些文献提出了比较明确的补充条件,如文献[3]中所述,用一个阻值RK=UK/IK的电阻元件来替代是有条件的,即该支路必须是耗能的。本文的思路是:“在未被替换二端网络中含有独立激励源的情况下,不管被替换二端网络是发出还是吸收功率,均可以用一个阻值为RK=UK/IK的电阻(Uk和Ik对Rk相关联)替代。”需要说明两点:一是即使被替换二端网络是发出功率的情况,那么替换原二端网络的是值为UK/IK的负电阻或者负阻抗。二是如果对应的是交流电路,则是用复阻抗ZK=UK/IK来替代原二端网络。
文献[3]用了一个错误的例子,得出了不严谨的结论,即耗能支路才可以用电阻元件来替代。图3是文献[3]的原图,文中认为支路1、支路2和支路3分别可以用6 Ω、6 Ω与8 Ω的电阻来替代;支路2和支路3可以用6 Ω和8 Ω的电阻替代,但是支路1用6 Ω电阻替代后改变了原电路的解。从图2容易看出,在支路1的电压和电流在非关联的情况下,应该用-6 Ω的电阻而不是6 Ω的电阻来替代,这样才不会改变原电路的解,原文忽略了负电阻在电路分析中的应用。至于用电阻在替代原二端网络时为什么要求被替换二端网络中含有独立激励源,道理很简单,因为当一个电路中没有了激励源,自然无法体现响应。从能量的角度看,没有原始能量的存在,电路传输转换能量的本质作用自然无法实现。

图3 文献[3]的例子
在交流电路分析中,我们运用替代定理时自然而然可以将原二端网络用阻抗值为ZK=UK/IK的线性复阻抗来替代。综上,如果考虑负电阻或者负阻抗的应用,不妨在含有独立激励源的二端网络中,用电阻RK=UK/IK或阻抗ZK=UK/IK来替代原二端网络,如图4所示。
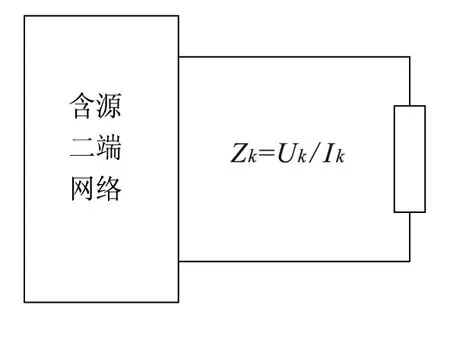
图4 用电阻或阻抗替代原二端网络
三、避免改变原电路的解
关于替代定理的成立条件,有些教材和文献并没有提及,部分文献给出的替换定理附加条件是:“各支路电压、电流在替代前后应保持唯一”,[4]它要求电路替代前后具有唯一解,此条件的出发点是防止替代后可能增加电路的解或者使电路有无数个解的情况出现。
例2,如图5所示,如果当未被替换二端网络出现无伴电源,则可能出现几个电压源直接串联或几个电流源直接并联的情形,易知此时未被替换二端网络的电流或电压有无数个解。由基尔霍夫电流定律和基尔霍夫电压定律,可推导并证明替代定理的正确性。逻辑命题应该完整并严谨,在叙述、推导和应用过程中有必要加入合适的补充条件,但补充条件使替代定理在很多场合和应用中受到限制。本文的想法是,不管原电路有唯一解、多解的情况,只要选择恰当的替换形式,可以保证不改变原电路解的情况下使用替代定理,让原电路得到化简。若图5中N是电压源,用电流源或电阻替代;若图5中N是电流源,用电压源或电阻替代。这样替代后,电路替换前后未替换部分电路的解保持不变。

图5 例2电路图
例3,在图6的电路中:

I3=U1(1-K)/R3.
当电路参数满足分母不等于0且电路具有唯一解的条件时,可以分别用电压源、电流源和电阻来替代U2右边端口。当电路参数满足电压电流表达式的分母和分子都等于零的条件时,电路具有无穷多解,表达式为US=R1I1+R2I2,此时只能用电压源替代U2右边端口,替代后未替换部分电路的解保持不变,其表达式仍然为US=R1I1+R2I2。当电路参数满足电压电流表达式的分母等于零而分子不等于零的条件时,电路无解;如果电路无解,则无法应用替代定理化简电路。综上所述,在电路有解的条件下,通过适当选择替换形式,在不改变原电路解的前提下,任何二端网络都可以运用替代定理化简。

图6 例3电路图
四、结语
替代定理可表述为:对于任何线性和非线性电阻电路,其中第k条支路的电压Uk和电流Ik已知,那么这条支路就可以用一个具有电压等于Uk的独立电压源,或者用一个具有电流等于Ik的独立电流源替代,替代后电路中全部电压和电流均将保持原值。以下则可以作为定理的补充说明:若被替换二端网络含有受控源的控制量,则该控制量可用Uk或电流Ik的线性组合表示;若考虑用电阻来替换二端网络,则未被替换二端网络中应含有独立激励源;若通过适当选择替换形式,在不改变原电路的解的前提下,任何有解的二端网络都可以运用替代定理化简。通过对定理的补充说明,加深对定理内涵的理解和对定理使用过程合理性的认识。
[1]邱关源.电路[M].5版.北京:高等教育出版社,2006:88-90.
[2]钟洪声,吴涛,孙利佳.简明电路分析[M].北京:机械工业出版社,2014:116-119.
[3]徐永谦,万延.关于《电路基本分析》中的替代定理问题的讨论[J].科技创新导报,2008,02(a):147.
[4]张柏顺,刘泉.再谈替代定理[J].电气电子教学学报,2003:101-103.
(责任编辑 邓 颖)
Some Discussions on Application of Substitution Theorem
Jian Zhimin1Lu Guangbao2
(1. Department of Mechanical and Automation Engineering, Zhangzhou Institute of Technology, Zhangzhou, Fujian 363000; 2. Fujian University of Technology, Fuzhou, Fujian 350118)
The substitution theorem is one of the important circuit theorems. There have always been relative discussions, whose focus is on the application and on whether the supplementary conditions should be added. Considering that the theorem is used for judgment and reasoning, from the perspectives of integrity and scientific rigor, and based on the actual teaching and research experience, the paper puts forward the ideas and opinions of the substitution theorem from three aspects: the first is the substitution of two terminal network containing controlled amounts; the second is the replacement with an appropriate resistor; the third is a flexible choice of substitution forms so as to avoid changing the original circuit.
substitution theorem; controlled amount; resistance substitution; substitution form
10.16169/j.issn.1008-293x.j.2017.11.020
G423.3
A
1008-293X(2017)11-0109-04
2016-10-09
简智敏(1979- ),女,福建南靖人,漳州职业技术学院机械工程及自动化系讲师,研究方向:电气工程及自动化。

