开关磁阻电机的调幅电压斩波控制
,,,
(福州大学 电气工程与自动化学院,福建 福州 350108)
1 引言
开关磁阻电机(SRM)的兼有传统交直流调速系统的优点——结构简单、成本低、效率高、调速性能好,已有正式的产品应用于电动汽车、航空工业、家用家电、纺织机械等各个领域,显示出强大的市场潜力和科研价值[1]。但是SRM内部磁场的非线性使得转矩和磁链是定子相电流和转子位置的难以解析的非线性函数,有别于传统的电机。因此,SRM研究和设计的主要发展方向是完善SRM设计理论,引入先进控制策略,加强实用无位置传感器技术的研究,减小SRM振动和噪声以及加强铁心损耗的理论研究等[2]。传统的控制方式如电流斩波控制(CCC)、电压斩波控制(CVC)和角度位置控制(APC)方式存在转矩脉动和稳态误差大的问题,而新型的瞬时直接转矩控制又因为电机转矩无法精确计算和测量而不能实际应用,因此,引入先进的控制策略是提高SRM的静态和动态性能指标的关键[3]。文献[4]提出了一种基于RBF神经网络的SRM角度优化控制方法,通过MATLAB/simulink设计了一个以转速误差和转矩作为输入、以最优关断角作为输出的RBF神经网络,实现了关断角优化来达到减小脉动的目的。文献[5]根据SRM不同的运行状态对目前国内外所研究的无位置传感器方法进行了讨论和分类,并指出了各种方式的优缺点。文献[6-8]阐述了基于转矩分配函数方式的SRM转矩脉动抑制方法,给出了采用转矩闭环实现期望转矩跟踪的转矩脉动减小控制系统设计。本文在传统的电流斩波和电压斩波控制方式基础上,设计了基于无位置传感器的调幅电压斩波智能控制器,通过改进的单神经元自适应PID使电机稳态误差减小,通过使电流波形优化来提高电机效率和出力,同时该控制方式下的无位置传感器的设计也相对简单有效。
2 SRM的基本控制方式
SRM在起动和低速运行时通常采用CCC和CVC方式。CCC方式通过给定允许的电流上限幅值iH和电流下限幅值iL来控制相电流保持在电流限内,当相电流大于iH时关断控制器的主开关器件,电流下降;当相电流小于iL时,开通主开关器件,电流上升,进而实现对电流和磁链的控制,以达到控制电磁转矩的目的。CCC方式下的相电流波形如图1所示。
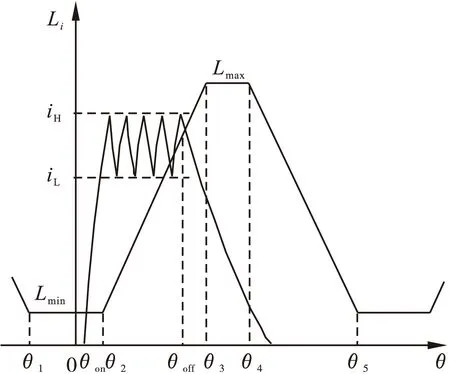
图1 CCC方式下的相电流波形
CVC方式通过调节方波信号的占空比来调节相绕组的平均电压,进而达到调节转速和转矩的目的。占空比越大,主开关器件导通时间越长,电压的平均值也就越大。CVC方式下的相电流波形如图2所示。
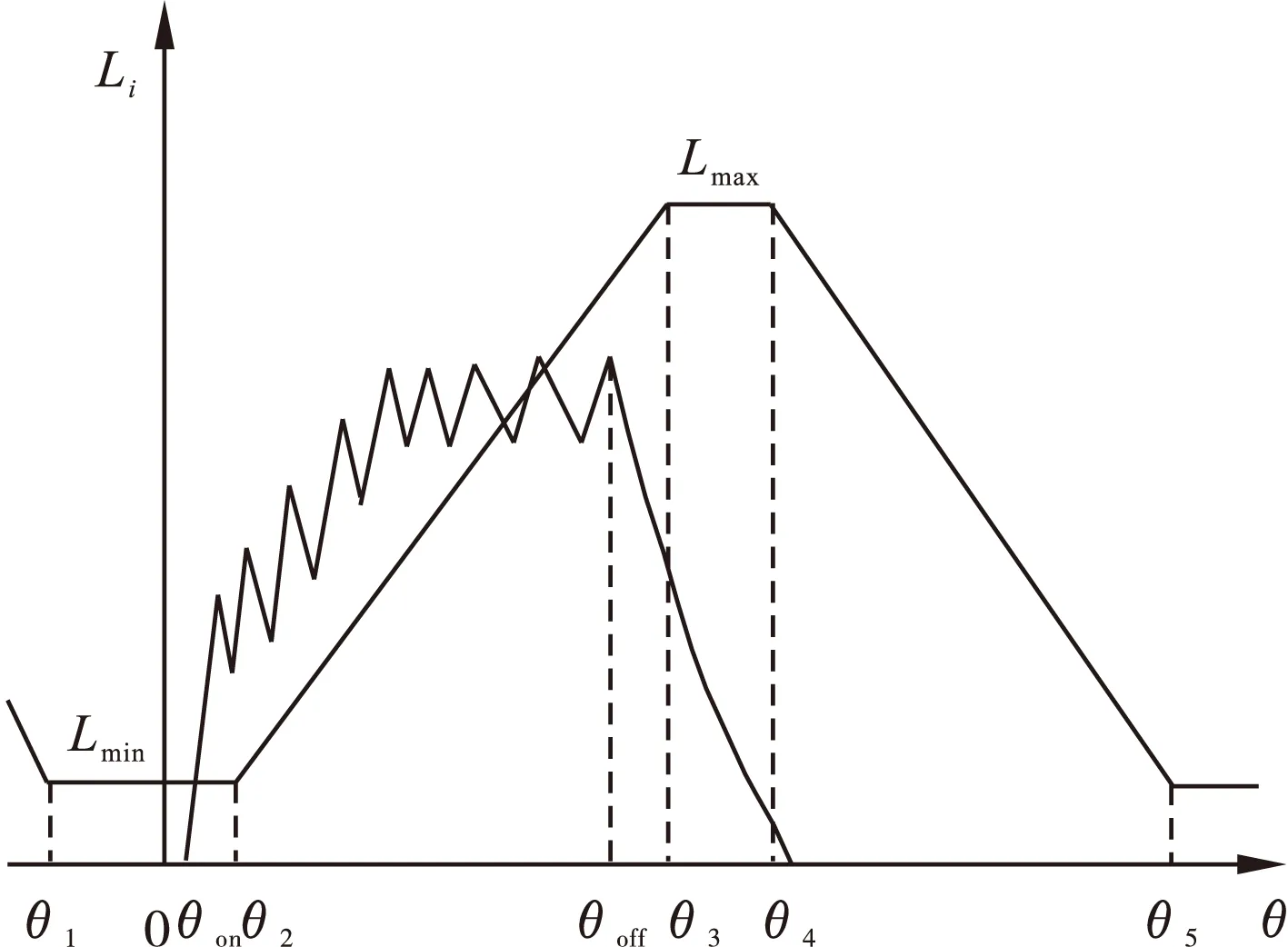
图2 CVC方式下的相电流波形
由SRM的转矩理论分析可知,在电感上升区域单相电流产生的瞬时转矩可表示为:
T≈-0.5i2dL/dθ
(1)
由此可知,如果忽略磁路饱和对电感L的影响,当电感的变化率为定值即在电感上升区域时,SRM的瞬时转矩与电流的平方成正比。因此,通过优化电流波形、减小电流斩波限即可在一定程度上减小瞬时转矩脉动。由图1可知,CCC方式下的相电流波形是一个平顶波,这样转矩脉动小,近似恒转矩起动,但其在稳态时无法固定电流斩波频率,斩波频率会随着电流误差的增大而增大,这对消除噪声和稳态误差非常不利。可控性能好是CVC最显著的特点,可以通过控制占空比和斩波频率来调节电机转速和消除负载扰动,且其动态响应速度快。然而由图2可以看出,CVC方式在电机起动时电流脉动大,导致转矩脉动也很大。
本文结合了CCC方式在起动时转矩脉动小和CVC方式在稳态时可控性能好的优点,提出了基于改进的单神经元自适应PID的调幅电压斩波控制方式,有效的提高了SRM的稳态和动态特性。
3 调幅电压斩波控制方式
此种控制方式下的相电流的开通角θon和关断角θoff为固定值。在电机起动时,固定电流上限幅值iH为允许的最大电流值,每当相电流达到iH,将主开关器件关断一定的时间T,然后再导通开关器件。根据公式Ldi/dt=U,直流电压U和电流下降时间T(dt)不变,在电感上升区域L逐渐变大,那么di将逐渐减小,因此在起动时,电流波形近似于一个斩波限逐渐减小的平顶波,转矩脉动也相对较小,接近恒转矩起动。当达到额定转速时,通过调节电流上限幅值iH,进而调节电流的上升时间即类似于调节CVC方式下的斩波频率,从而达到消除稳态误差和负载扰动的目的。在起动和低速运行时,调幅电压斩波方式可以通过选择开通角和关断角使通电区间均在电感曲线的上升区域,占据其大部分或全部,进而能够使电机的效率和出力进一步提升。在实际应用中,当转速较高时,部分相电流可能进入电感下降区,其解决方法是适当的提前关断角。其结构框图如图3所示。
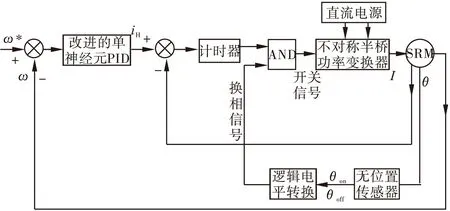
图3 系统结构框图
4 复合自适应PID
由于SRM内部磁场严重的非线性,控制方式的改变会导致其参数、结构都发生变化,固定参数的传统PID调节器无法得到理想的控制效果。比如,对某一种类结构的SRM或在某一速度范围内整定好的比例、积分、微分参数并不能保证其可在大范围内调节,也不能确保系统有良好的动特性。
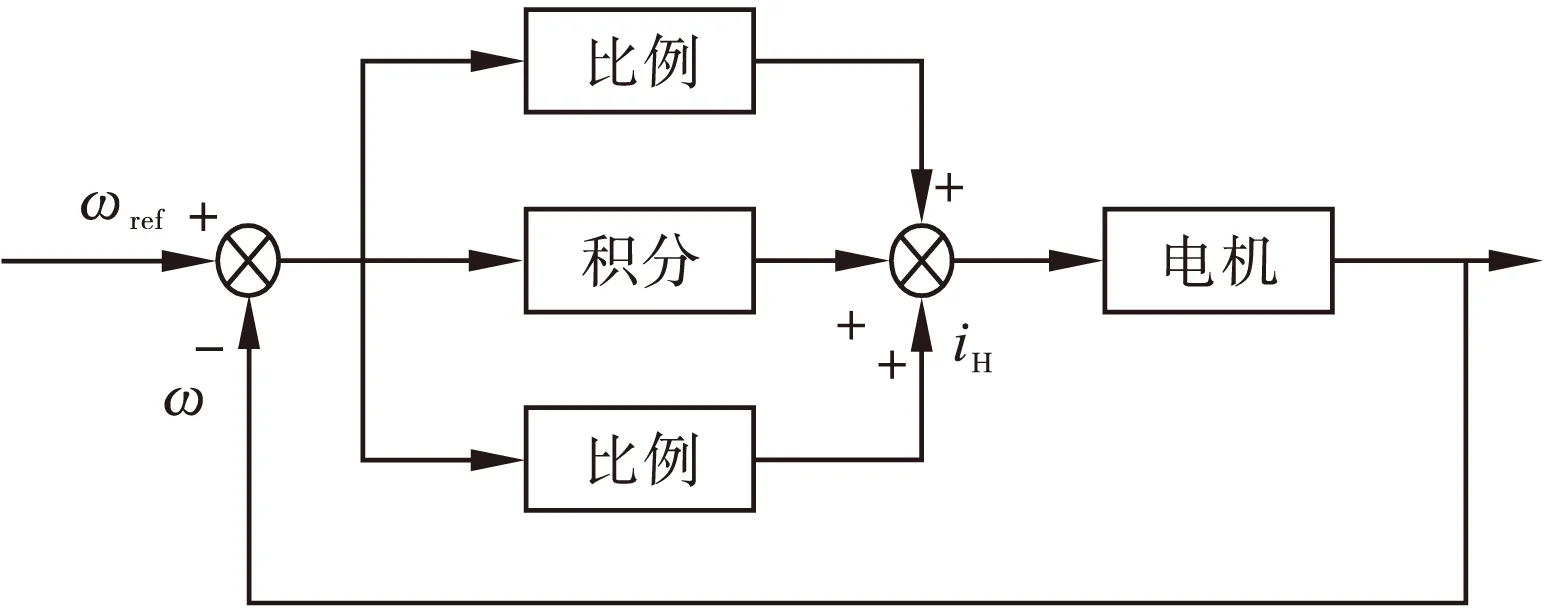
图4 PI控制器在电机调速中的结构
传统的PID控制器如图4所示,可以看出,PID控制器的输出为转速误差比例、积分和微分的线性组合,图中转速误差为:
e(k)=ωref-ω
(2)
对于离散系统,PID控制器的输出表示为:
(3)
k代表采样次数;ki、kp、kd分别为比例、积分和微分系数;T为采样周期。
单神经元PI控制器能够很好的适应SRM的非线性,不仅易于实时控制,而且拥有神经系统控制的鲁棒性和较强的自适应能力,但其在系统接近稳态和稳态时,由于稳态误差总是存在,调节参数不停的改变,使得控制器的输出上下波动,造成系统的稳态特性差。在实际情况中,单神经元比例系数k的值一般都是依赖于调试经验,因此单神经元PI控制器并不能算作自适应控制,其结构框图如图4所示。

图5 单神经元PID控制器结构
其输出由公式可以表示为:
(4)
其中,k代表采样次数;K为单神经元比例系数,常取K>0,K越大则快速性越好,但超调量大,可能使系统不稳定。xi(i=1,2)表示系统的输入变量,具体计算方法如下:
(5)
其中,γi(i=1,2)对应于传统PI控制器的ki、kp,在增量式算法中为输入量的权值,单神经元PI控制器是通过对权值的调整来实现自适应自组织功能的,权值的计算公式为:
(6)
权值的修正公式为:
γ1(k)=γ1(k-1)+ηI·e(k)·u(k)·x1(k)
γ2(k)=γ2(k-1)+ηP·e(k)·u(k)·x2(k)
(7)
式中,ηI,ηP代表着ki,kp的学习速率。
本文结合了单神经元PI控制器动特性好和传统PID控制器静特性好的优点设计一种改进的复合自适应PID控制器,不需要控制对象的先验知识,不用提前给定或人工调节PID参数,通过在线辨识和自学习、自适应能力对比例系数k实时调整。
当转速误差很大或者负载转矩发生变化时,k相应的增大,以加快系统的响应速度从而使系统快速收敛,同时为了进一步调高系统的响应速度,对单神经元PID的输出引入了动量因子;当误差很小时,由于稳态性能大部分取决于积分增益ki,所以对ki采用自学习的方式,提高稳态性能,而比例系数kp此时可以取零或者任意一个较小的正数。其切换时机如表1所示。

表1 复合PI控制器的切换规则
公式修正以后的单神经元PI控制器的输出为:
(8)
式中,ɑ为动量因子,可取0.95。γ(k)为修正后的单神经元比例系数,其自学习公式为:
(9)
积分增益ki的自学习方法为:
(10)
5 仿真与分析
仿真图如图6所示,其中定子电阻Rs=0.1(ohm),电源电压U=110(V),转动惯量J=0.0017(kg·m2),摩擦系数F=0.008(N·m2),Lmax=0.17(H),Lmin=0.0078(H),最大电流1.5A,给定转速300r/min31.4(rad/s);电机带1N·m负载起动,在0.15s时负载转矩突变为3N·m,0.2s时恢复为1N·m。

图6 仿真结构图
图7为传统控制方式(CCC和CVC)下的单相电流波形和本文控制方式下的单相电流波形。图8为传统控制方式下的转速波形,图9为本文控制方式下的转速波形。
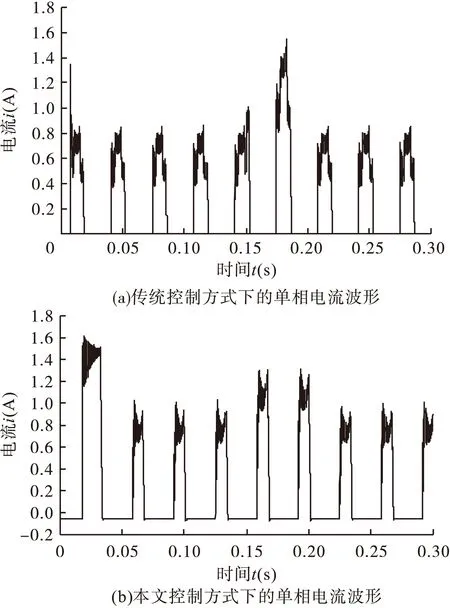
图7 单相电流波形
由图7可以看出,本文控制方式下相电流波动小,转矩脉动也会相应的减小。由图8和图9可以看出,本文控制方式下SRM在起动时的转速响应速度快,起动时间短;在稳态时,转速稳态误差小;在负载发生变化时,抗干扰能力和自适应能力强。
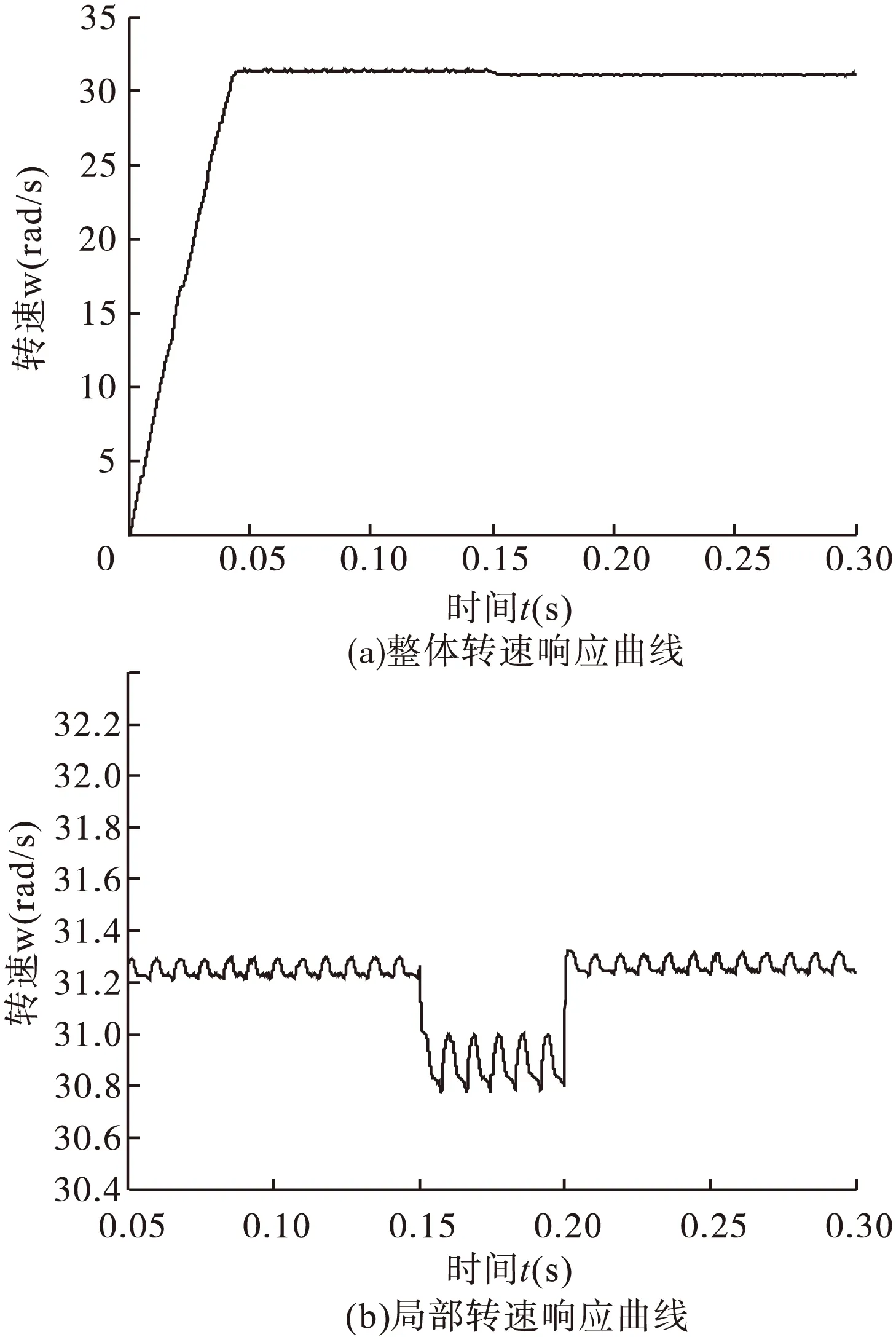
图8 传统控制方式下的转速波形
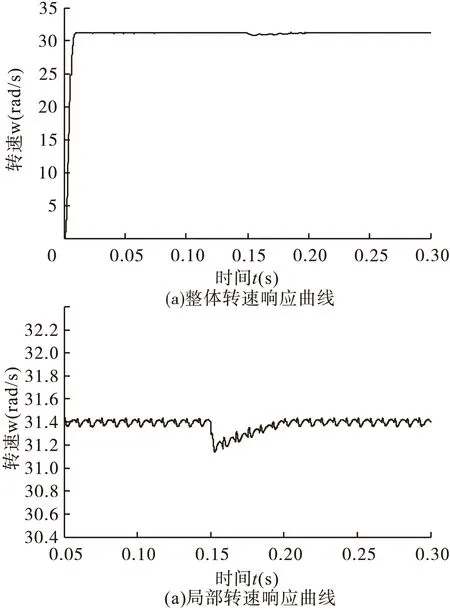
图9 本文控制方式下的转速波形
6 结论
本文在传统的电流斩波和电压斩波控制方式基础上,设计了调幅电压斩波智能控制器,通过复合的单神经元自适应PID使电机稳态误差减小,通过使电流波形优化来提高电机效率和出力,同时该控制方式下的无位置传感器的设计也相对简单有效。仿真结果证明
了该方法的合理性与有效性,为实际SRM控制系统和无位置传感器的设计提供了新的思路。
[1] 吴建华.开关磁阻电机设计与应用[M].北京:机械工业出版社,2000.
[2] 王宏华.开关磁阻电动机调速控制技术[M].北京:机械工业出版社,2011.
[3] 陈昊.开关磁阻调速电动机的原理设计应用[M].徐州:中国矿业大学出版社,2000.
[4] 陈灵.基于开通_关断角度优化的开关磁阻电机控制策略的研究[D].中南大学,2010.
[5] 邓智泉,蔡骏.开关磁阻电机无位置传感器技术的研究现状和发展趋势[J].南京航空航天大学学报,2012,44(5):21-30.
[6] 郑洪涛,陈鑫.基于模糊神经网络开关磁阻电动机高性能转矩控制[J].控制理论与应用,2003,20:(4)541-546.
[7] 蒋静萍,张国宏.减小开关磁阻点动机低速时转矩脉动的新型控制策略[J].中小型电机,1999,26(6):22-26.
[8] 夏长亮,陈自然,李斌,等.基于RBF神经网络的开关磁阻电机瞬时转矩控制[J].中国电机工程学报,2006,26(29):127-132.

