基于MPGA的混合储能系统容量配置

(福州大学，福建 福州 350116)

1 引言

近年来，我国风电发展迅速，其装机容量在电力系统中的比例不断上升。由于风电功率具有波动性的特点，大规模风电厂的输出功率直接并入电网，会影响电力系统运行的稳定性和可靠性[1-2]。储能系统能够快速准确地补偿系统所需的能量，实现电能的平衡、稳定控制。然而单一的储能介质无法同时满足功率和能量需求，采用混合储能技术往往能达到较好的效果[3-4]。因此，在风场侧配置合适的混合储能系统装置，实现平滑风电并网功率，减少风电波动性对电网电力系统造成的冲击。文献[5]采用低通滤波方法分解母线波动电压，高频部分分配给超级电容，蓄电池承担低频部分能量。当混合储能系统不满足平抑条件时，风电并网波动功率由电网吸收。文献[6]采用下垂控制方法，利用超级电容快速充电的工作特性，保持母线电压稳定；同时实时检测超级电容的电压水平，使蓄电池对超级电容充电，保持超级电容的能量平衡。文献[7]采用滑动平均滤波方法分解风电输出功率，得到需要蓄电池平抑的低频功率；超级电容采用双环控制，稳定直流母线电压，承担高频波动功率。根据混合储能系统的运行状态，动态调节滑动平均窗口宽度T，优化混合储能能量分配，增强混合储能系统的平抑风电功率波动能力。

文献[8]提出了一种基于电压下垂法的直流微电网混合储能控制策略。该控制策略根据直流母线电压信息，利用超级电容快速补偿母线功率缺额的高频部分；通过蓄电池对超级电容进行能量补充，间接补偿母线功率缺额的低频部分。文献[9]风电输出功率通过一阶滤波环节之后，分解得到超级电容和蓄电池的功率；通过基于神经网络的混合储能系统的能量管理系统，动态调整了两个储能介质的充放电功率指令，使混合储能系统能处在良好的运行状态。

文献[10]根据超级电容和储能电池的充放电特性，采用低通滤波方法进行功率分配。考虑到混合储能系统的功率损耗，制定了并网功率调节模块，实时调节混合储能系统的能量状态。为了保证超级电容充放电能力，对混合储能的功率进行再分配，维持超级电容荷电状态处于较优水平。

在混合储能系统容量配置方面，文献[11]采用高通滤波器对风电波动功率进行分解，得到混合储能系统平抑目标；考虑到超级电容和蓄电池荷电状态，以荷电状态饱和度和功率参考值饱和度作为输入，利用模糊控制策略对平抑功率进行再分配；考虑混合储能系统的经济性，采用机会约束规划方法对混合储能系统的容量进行配置。文献[12] 基于实时的风电输出功率数据，采用低通滤波方法平抑风电功率波动，并分析了不同的滤波时间系数对风电波动平抑效果造成的影响；在评价混合储能系统平抑风电的效果时，提出了功率积分时间尺度和标准差两个评价指标。文献[13]以超级电容器和蓄电池混合储能系统在整个寿命周期内的成本为目标函数包括购买第批次储能元件及附属配件的一次投资成本储能元件由于老化和损坏造成的储能元件更换所产生的二次投资成本对失效的储能元件进行处理所产生的回收环保成本，建立混合储能系统的容量配置目标。文献[14] 并网风光发电中混合储能系统容量优化配置，以系统能量损失率及能量缺失率等运行指标为约束条件，根据全生命周期费用理论，建立储能装置的年均费用函数为目标函数，运用改进混沌优化算法对混合储能系统的容量进行配置。文献[15] 风电场复合储能系统容量配置的优化设计，提出了一种能够定量反映功率曲线平滑度的判据标准，综合考虑了复合储能系统的技术性能和经济性能，建立了反映复合储能系统特性参数-风电功率平滑度、复合储能系统成本特性的长期数学模型；通过遗传算法对该模型的目标函数进行寻优，从而得到复合储能系统最佳的特性参数组合。

上述文献对混合储能应用于平抑风电功率波动的控制策略展开研究并取得了一定成果。其中，混合储能系统的协调控制策略主要体现在频域的滤波方式，容量配置多采用传统的人工智能算法。但是采用滤波的方法具有延时现象，且分解得到的需要混合储能平抑的功率分量可能不一致，使混合储能系统承担额外的能量。传统的人工智能算法可以对配置混合储能容量进行配置，但可能出现早熟而陷入局部最优的缺陷。基于以上分析，本文采用超级电容优先充放电，当超级电容不能再充放电时，再令蓄电池在进行充放电的控制方式。不仅使得各储能介质优势互补，而且不增加混合储能系统的充放电能量；针对传统遗传算法可能陷入局部解的缺点，采用多种群遗传算法(MPGA)优化配置混合储能系统的容量。

2 混合储能系统平抑目标及控制策略

2．1 混合储能系统波动分量的选取

风电机组通常以最大风能捕获的模式运行，风电输出功率主要由实时风速决定的。风能具有的随机性、波动性，使得风电输出功率波动较大，直接并网势必对电网的电能质量以及调度造成影响。在风电侧接入混合储能系统，可以有效地抑制风电的波动性，使得风电并网功率满足要求。如图1所示，风电输出功率为PWind，需要混合储能系统平抑的功率PHybrid，以及风电功率经过平抑后的并网功率PGrid。

风电场正常运行状态下，其有用功率的最大变化率，应当满足电力系统安全稳定运行的要求。本文采用以风电并网标准为依据，对风电场输出功率为PWind进行分解的方法，即规定风电场输出功率1min波动不超过风电场装机容量的2%，30min不超过风电场装机容量的10%，得到需要混合储能系统平抑的功率PHybrid和满足要求的风电并网功率PGrid。如图2所示。

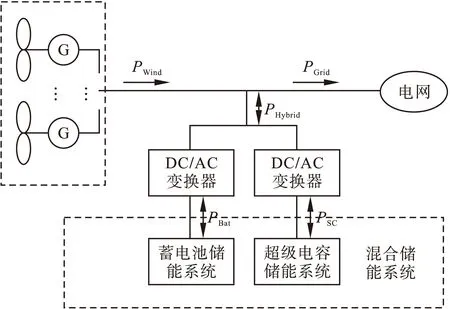
图1 风电/混合储能系统

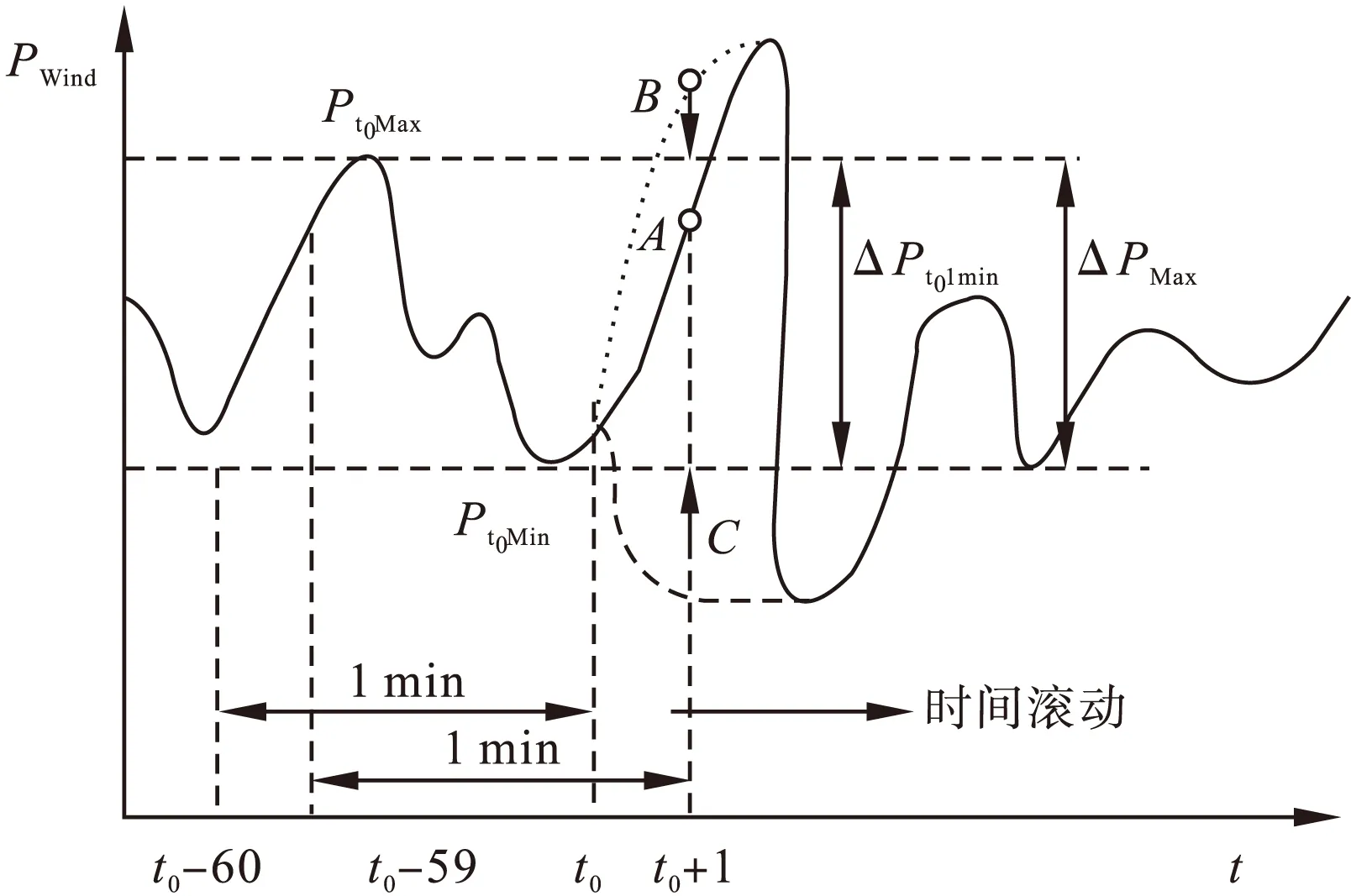
图2 1min风电场输出功率分解图

采样时间设置为1s，仿真时间以1min时间窗向前滚动，假设当前时间为t0，且在t0之前的波动满足并网要求，即以t0为终点，时间尺度为1min的功率波动量为ΔPt01min=Pt0Max-Pt0Min满足ΔPt01min≤ΔPMax，其中Pt0Max，Pt0Min分别为[t0-60,t0]时间内功率最大值和最小值。当时间为t0+1时，若输出功率为图中A点时，此时在以t0+1为终点的以1min时间窗内的功率变化量ΔPt0+1min≤ΔPMax，风电输出功率满足要求，此时混合储能系统的不出力；若输出功率为图中B、C点时，显然以t0+1为终点的以1min时间窗内的功率变化量ΔPt0+1min>ΔPMax，需要混合储能系统平抑剩余的功率；在B点输出功率为PHybrid=PB-Pt0Max，C点为PHybrid=Pt0Min-PC，此时t0+1时刻的功率分别为Pt0Max和Pt0Min。

本文基于某49.5MW风电场典型天的实时数据，以1min的波动要求为例，30min类似处理，验证波动量分解的有效性。风电并网标准1min内有用功率的最大变化率为ΔPMax=49.5×2%=0.99。采用上述方法对样本数据PWind进行分解，得到需要混合储能系统平抑的功率PHybrid和满足要求的风电并网功率PGrid，如图3所示。

2．2 混合储能控制策略研究

基于不同工作特性的储能介质，如能量型的蓄电池和功率型的超级电容，如何分配混合储能系统介质之间的功率，使得储能介质处于较优运行状态，混合储能系统具有较强的平抑风电功率波动的能力。本文采用超级电容优先充放电，当超级电容不能再充放电时，再令蓄电池在进行充放电的控制方式。该控制方式简单，而且可以充分利用超级电容充放电次数多，能量密度大的工作特性，使得在功率波动较小的情况下，蓄电池不动作，从而减少蓄电池的充放电次数，提高蓄电池的使用寿命，优化混合储能系统的整体性能。考虑到深度充放电和大功率充放电都会给混合储能系统造成损坏，设定了超级电容和蓄电池荷电状态和功率限制条件，其各自的荷电状态区间划分和功率约束如图5和表1所示，其中Pxrated为额定功率，SOCx为荷电状态，SOCxMax、SOCxMin为荷电状态上下限，ax=Pxrated/(SOCxmax-SOCxA),x为SC或Ba。

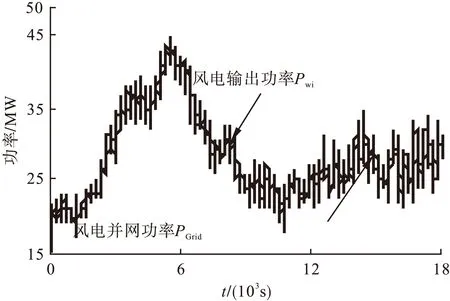
图3 风电输出功率分解图

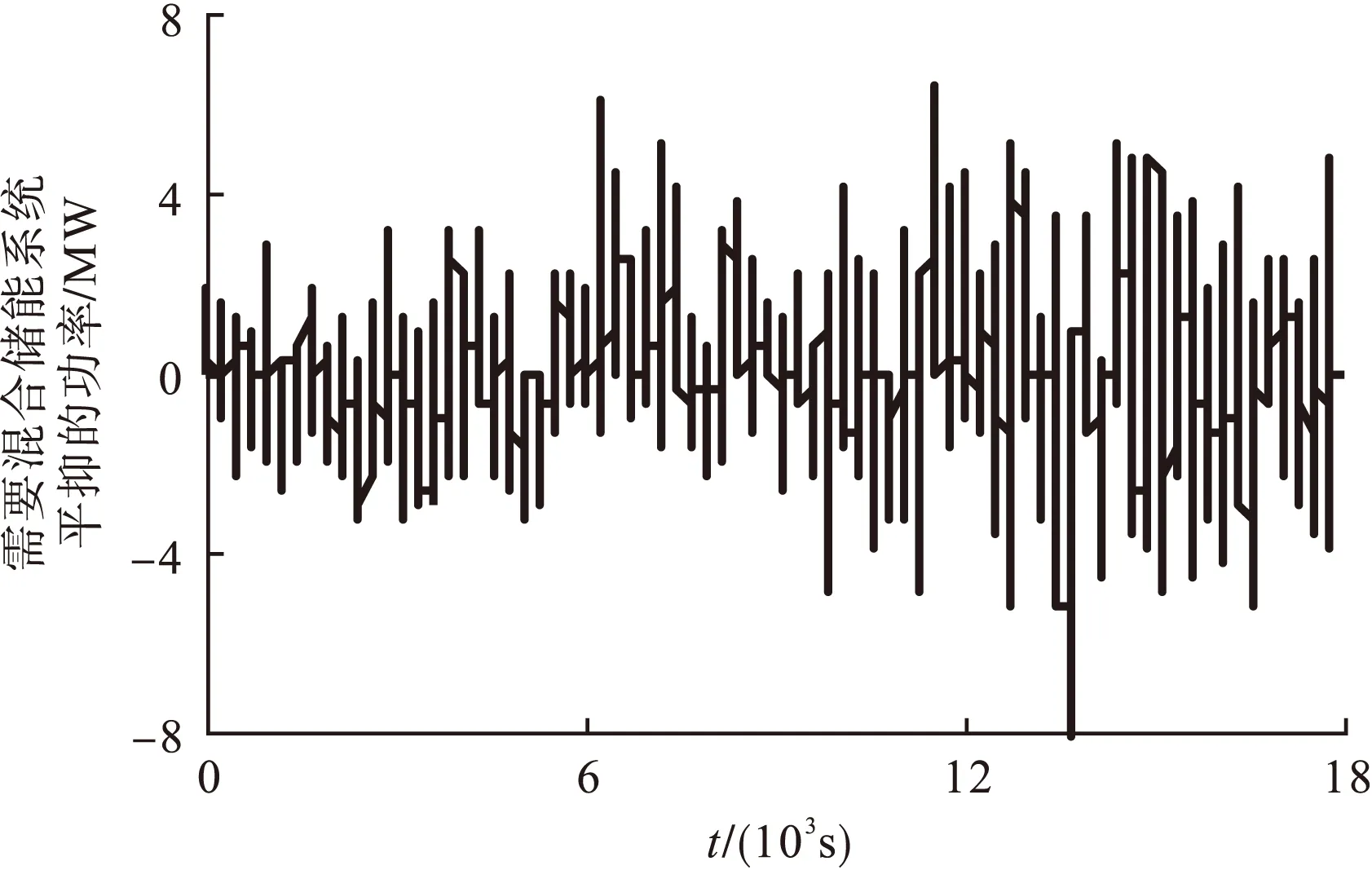
图4 需要混合储能系统平抑的功率

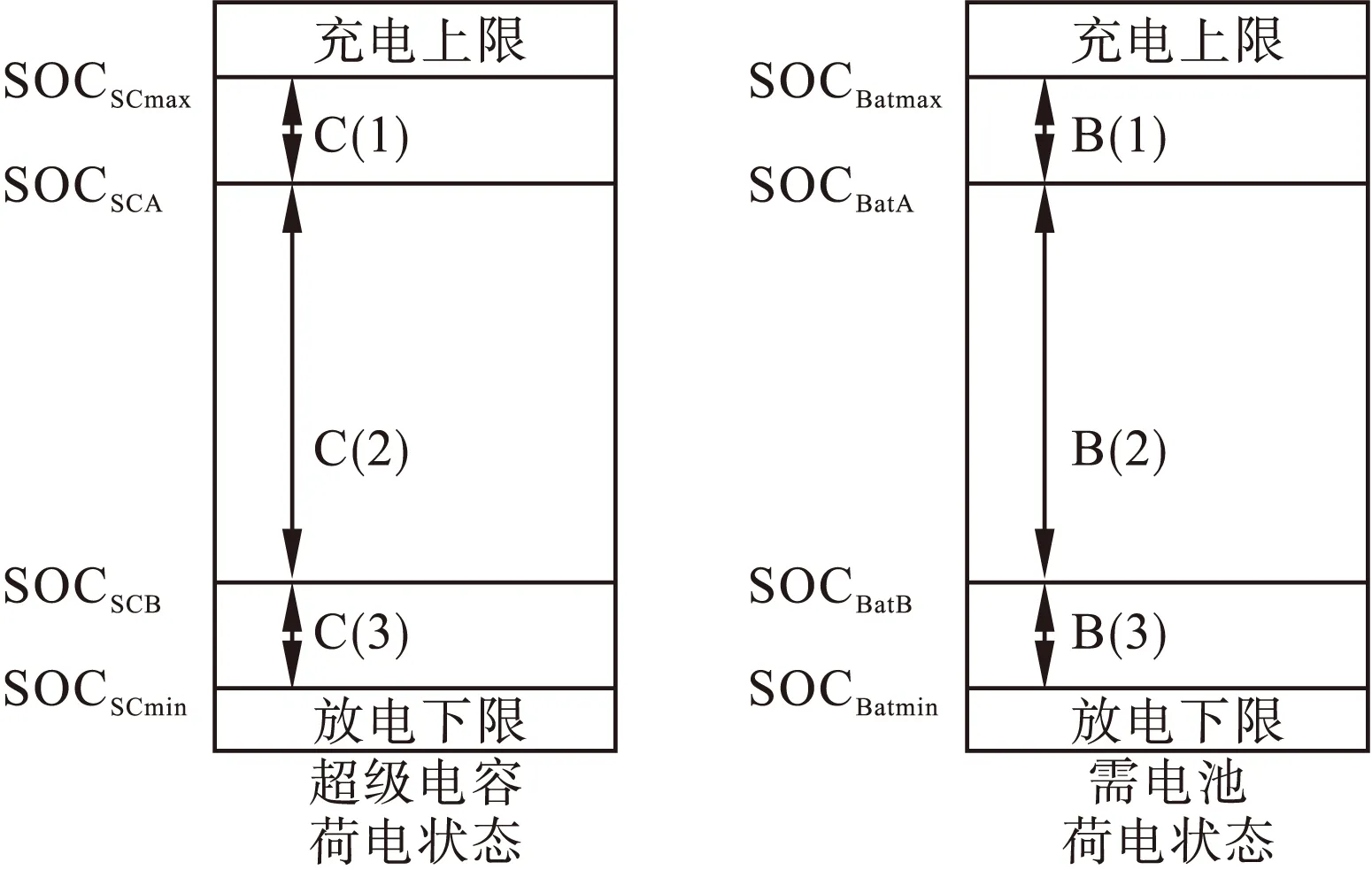
图5 混合储能荷电状态区间划分

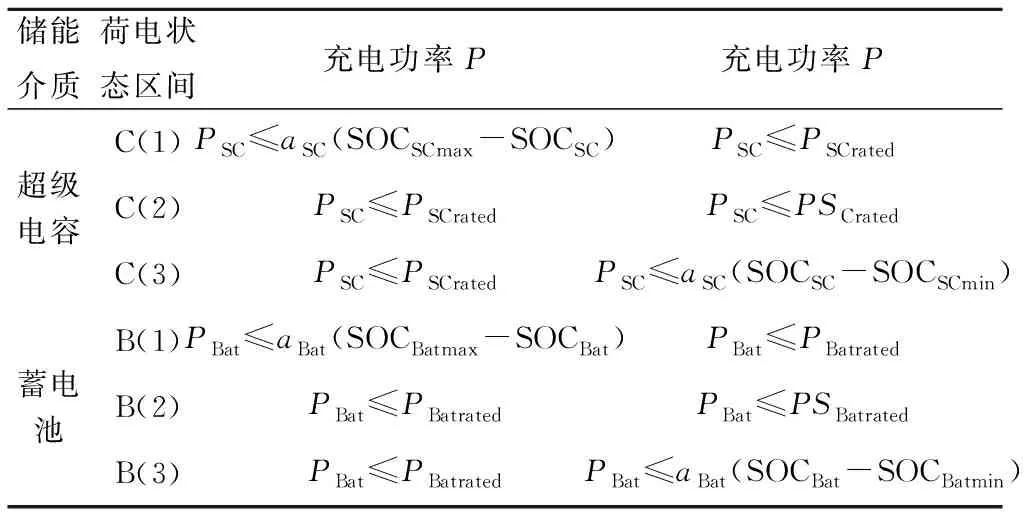
储能介质荷电状态区间充电功率P充电功率P超级电容C(1)PSC≤aSC(SOCSCmax-SOCSC)PSC≤PSCratedC(2)PSC≤PSCratedPSC≤PSCratedC(3)PSC≤PSCratedPSC≤aSC(SOCSC-SOCSCmin)蓄电池B(1)PBat≤aBat(SOCBatmax-SOCBat)PBat≤PBatratedB(2)PBat≤PBatratedPBat≤PSBatratedB(3)PBat≤PBatratedPBat≤aBat(SOCBat-SOCBatmin)

3 混合储能系统容量配置

3.1 混合储能系统数学模型

利用混合储能装置平抑风电波动可以收到很好的效果，然而混合储能系统的成本比较高，合适的混合系统容量至关重要。因此，本文以混合储能系统的成本最小作为目标函数，将超级电容、蓄电池的额定功率和超级电容、蓄电池的额定容量作为决策变量，对混合储能系统进行容量配置，其表达式为:

f=CPSCPSCrated+CPBatPBatrated+CQSCQSCrated+

CQBatQBatrated

(1)

式中：QSCrated、QBatrated分别为超级电容、蓄电池的额定容量；f为混合储能装置总成本费用；CPSC、CPBat分别为超级电容和蓄电池额定功率单价；CQSC、CQBat分别为超级电容和蓄电池额定容量单价。

为了衡量应用混合储能系统后风电功率平滑的效果，以风电功率输出平滑率η作为评价指标，其值为混合储能系统无法完全吸收的功率剩余量ΔPHybrid的绝对值方差与风电并网功率PGrid绝对值方差的比值[12]，即

(2)

风电功率输出平滑率η是目标函数中决策变量的函数，表达式如下：

η(PSCrated,QSCrated,PBatrated,QBatrated)≤α

(3)

若α为零，说明混合储能系统完全吸收风电波动分量；α取值较少时，说明应用混合储能系统后风电功率平滑效果较好，相反会相应地增加系统的容量。考虑到经济性，α取值在合理的范围内即可，本文取α=0.01。

混合储能系统中，超级电容的寿命比蓄电池长，允许充放电次数较多；而蓄电池寿命较短，允许的充放电次数有限，对蓄电池的充放电次数的限制是必要的。可以根据实际情况，设置蓄电池的充放电次数，保护蓄电池，提高混合储能系统的寿命。

N(PSCrated,QSCrated,PBatrated,QBatrated)≤N0

(4)

式中N0为蓄电池充放电次数限制。

基于上述分析，混合储能系统的数学模型为:

f=CPSCPSCrated+CPBatPBatrated+CQSCQSCrated+CQBatQBatrated

(5)

2．2 多种群的遗传算法配置混合储能系统容量

遗传算法(SGA)是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法，非常适用于处理传统搜索算法难以解决的复杂和非线性优化问题。然而常规的遗传算法对新空间的搜索能力有限，可能会出现早熟，存在收敛到局部最优解的缺陷。针对遗传算法早熟收敛的问题，一种多种群遗传算法(MPGA)可以用来取代常规的遗传算法。

多种群遗传算法(MPGA)突破SGA仅靠单个群体进行遗传进化的框架，通过设有不同控制参数的多种群协同进化，同时兼顾算法的全局搜索和局部搜索。因此，本文采用多种群的遗传算法(MPGA)，对上述带有约束条件的混合储能成本目标函数进行寻优，获得混合储能系统成本最小的混合储能系统配置方案，其算法流程框图如图6所示。

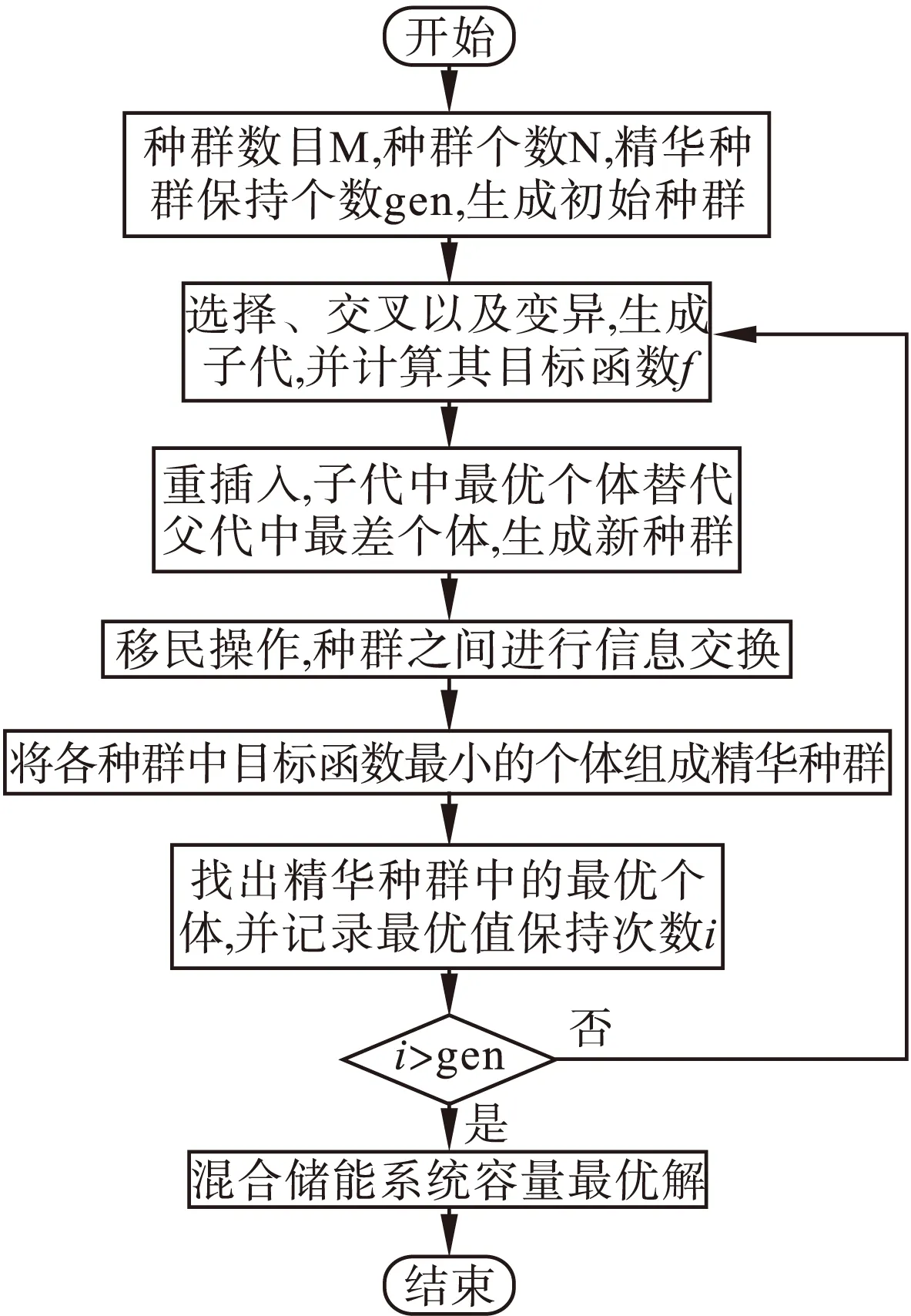
图6 MPGA的算法流程框图

算法流程具体如下：

(1)初始化。各种群中的个体都是四个决策变量在约束区间内随机产生的的数值，即超级电容、蓄电池的额定功率以及超级电容、蓄电池的额定容量；设定合适的种群数目，随机生成初始种群。

(2)计算初始种群中每个种群里个体的对应的目标函数值，即混合储能系统的配置成本。群。

(3)对每个种群进行选择、交叉以及变异操作，得到新种群。

(4)重插入操作。计算新种群中每个种群里个体的对应的目标函数值，将新种群目标函数值最小，即成本最小的的个体代替旧种群目标函数值最大的个体。

(5)移民操作。将各种群最优个体引入其他的种群中，实现种群之间的信息交换。

(6)精华种群。把各种群中最优个体组成精华种群，找出精华中最优个体，记录其值的保持次数。

(7)最优解。若当前精华种群最优值保持次数大于设定次数时，则停止计算，此时最优值就为算法最优解，即混合储能系统容量的最优解，否则重复3)-6)。

3 算例分析

3.1 容量配置算法的比较

本文采用Matlab/simulink进行仿真分析，风电输出样本数据的时间选取为5h，对于49.5MW的风电场，超级电容和蓄电池的功率都应该小于49.5MW，即PSCrated∈[-49.5,49.5]，PBatrated∈[-49.5,49.5]；超级电容和蓄电池的额定容量都应该小于247.5MWh，即QSCrated∈[0,247.5]，QBatrated∈[0,247.5]。其他参数设置如表2所示。

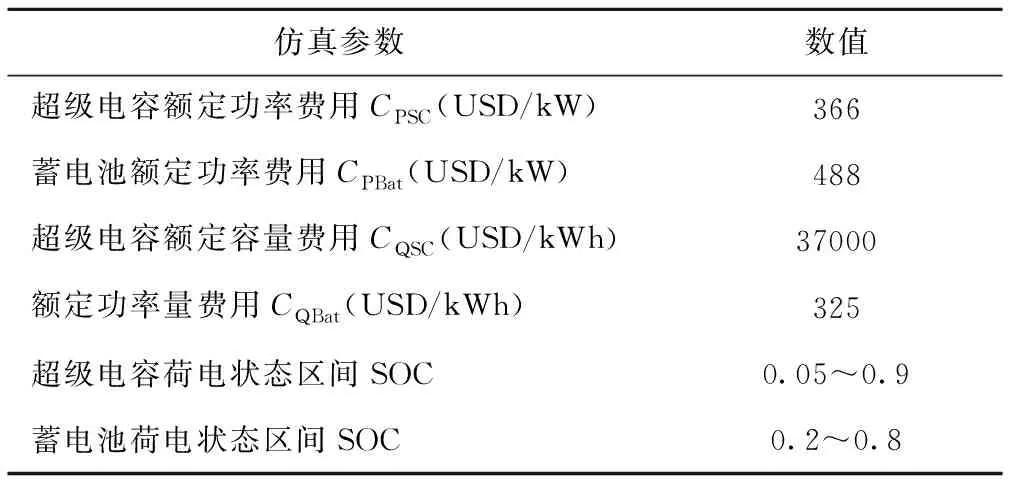
表2

基于上面的参数设置，分别采用多种群遗传算法和常规遗传算法对混合储能系统的数学模型进行优化配置。设置多种群遗传算法的最优值相同保持代数不少于10，各种群的种群个体数目为40个，种群数目为10，常规遗传算法种群个体数目为40个，进化次数为200次，得到如图7所示。

由图6，7可知，传统的遗传算法在优化容量配置时，陷入了局部最优解，其寻优得到的容量配置比采用多种群算法得到的配置容量大，具体数值如表3所示。其最主要的原因在于采用多种群遗传算法，各种群分散到区间的各个区域，避免陷入局部解，利用种群之间的信息交换，实现全局最优解的寻优。

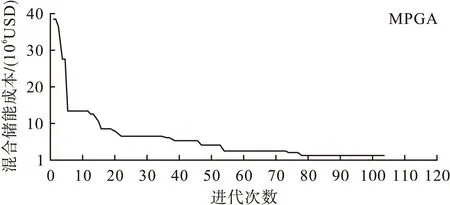
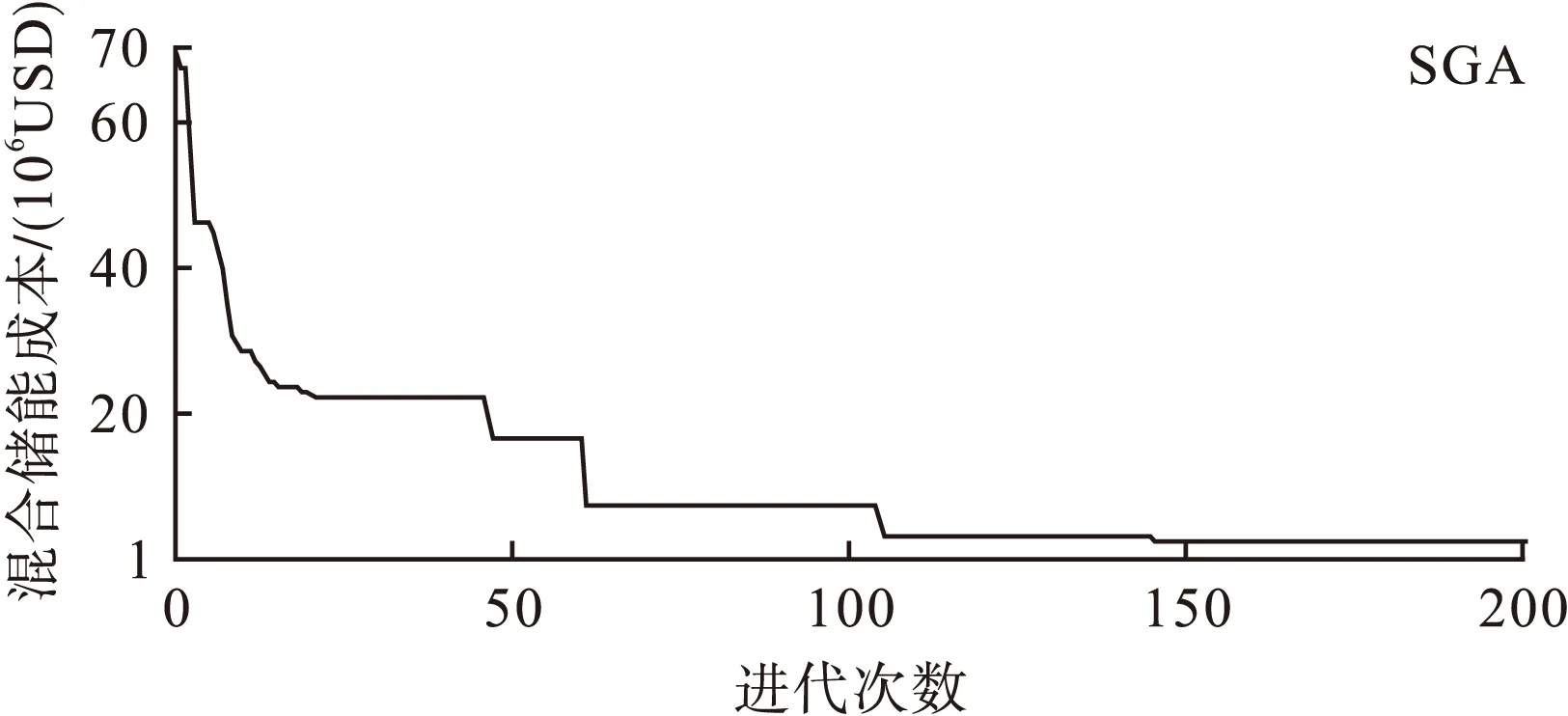
图7 多种群算法容量配置寻优过程

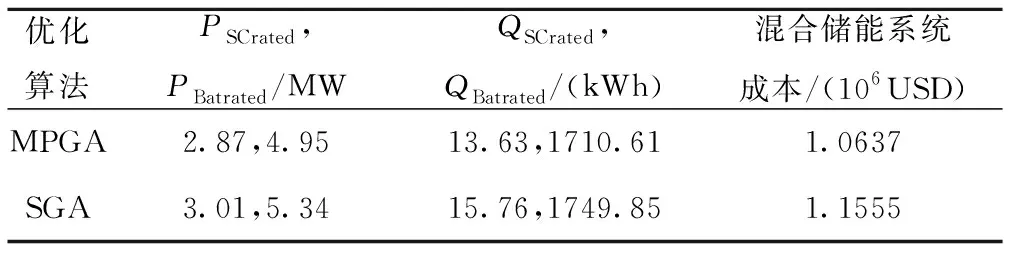
优化算法PSCrated,PBatrated/MWQSCrated,QBatrated/(kWh)混合储能系统成本/(106USD)MPGA2.87,4.9513.63,1710.611.0637SGA3.01,5.3415.76,1749.851.1555

在混合储能数学模型中，蓄电池的充放电限制次数N的设置会影响到容量配置的效果,设置N为不同数值，进行多次仿真，如图8所示。在充电次数56之前，混合储能系统成本变化趋势较大；在充电次数56之后变化缓慢。因此，充放电次数选为56时，混合储能系统得到最合适的配置容量，其值为PSCrated=2.87MW、PBatrated=4.95MW、QSCrated=13.63kWh、QBatrated=1710.61kWh。

3.2 控制策略的比较

根据上述采用多种群遗传算法得到的混合储能系统配置容量结果，即超级电容和蓄电池的额定功率和额定容量设定分别为PSCrated=2.87MW、PBatrated=4.95MW、QSCrated=13.63kWh、QBatrated=1710.61kWh，分别采用本文采用的方法和低通滤波的方法进行仿真，验证本文采出的控制策略的有效性。采用低通滤波方式时，超级电容和蓄电池的荷电状态区间划分和功率限制条件相同，其低通滤波系数设置为0.01。

采用低通率方式，超级电容和蓄电池各自承担分解得到的能量吸收和释放；分解得到需要的超级电容平抑的能量较大，但其容量不够，剩余的能量过多，造成并网功率波动大，如图11(b)所示；分解得到需要的蓄电池波动功率波动性较大，造成其充放电次数相对较多，蓄电池的充放电次数分别为56和83次。本文的控制方法简单，储能介质能优势互补，使得混合储能系统处于较优的运行状态且平抑风电波动效果较好。

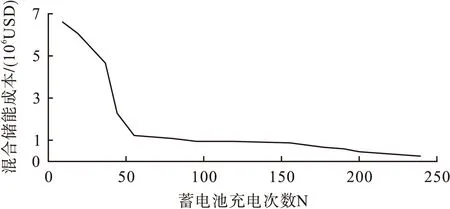
图8 蓄电池充放电次数与混合储能系统成本之间的关系

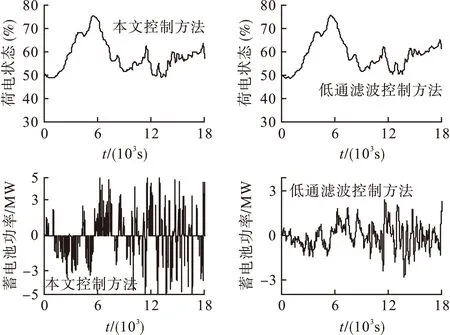
图9 蓄电池运行状态比较

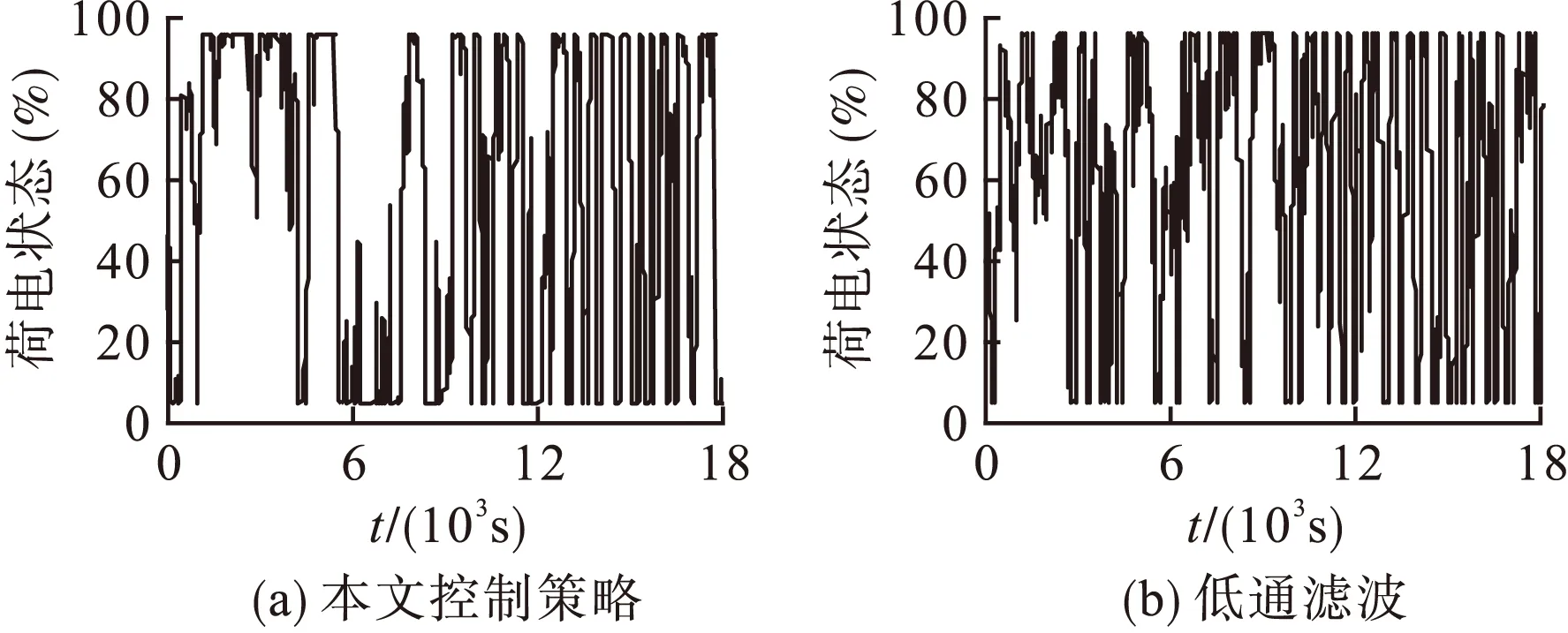
图10 超级电容的荷电状态比较

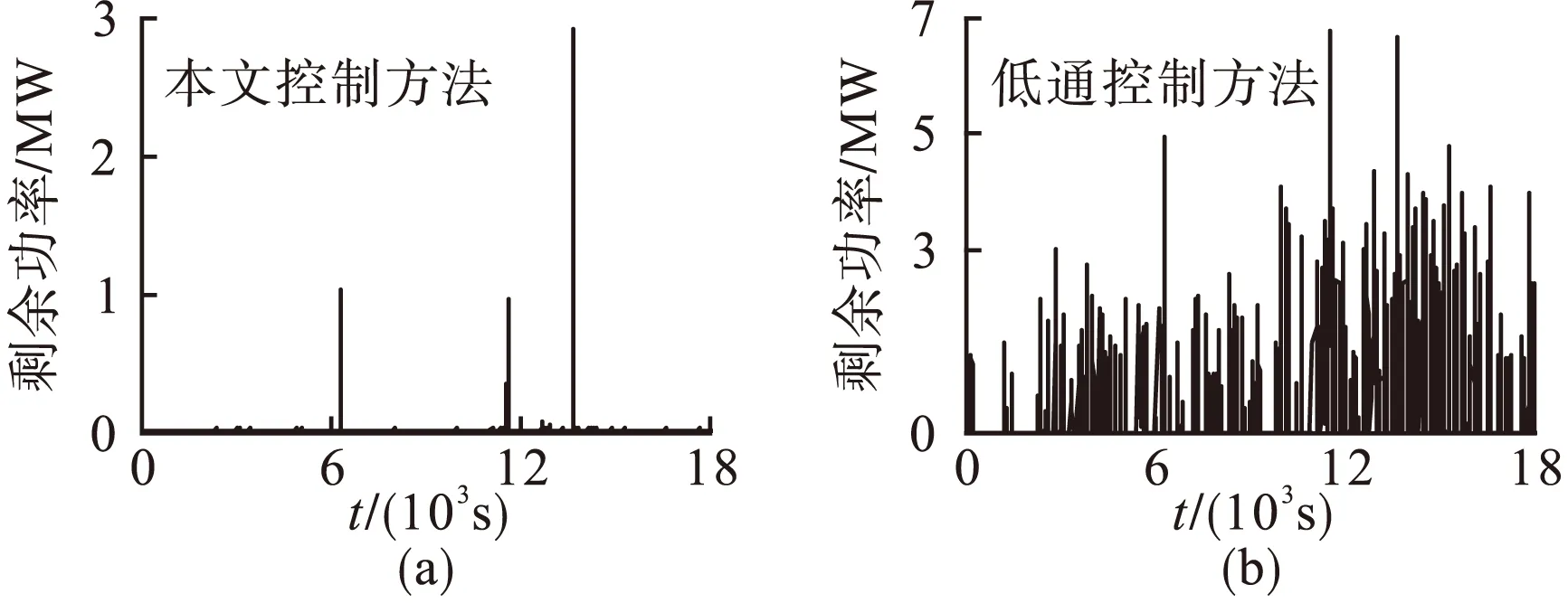
图11 混合储能系统的平抑效果比较

4 结论

针对风电输出功率的波动性，本文提出的波动量分解的方法，在考虑风电并网要求的情况下，分解得到混合储能系统的功率平抑目标。

采用超级电容器优先充放电，当超级电容器不能再充电或是放电时，再令蓄电池充放电的控制方式，通过蓄电池和超级电容之间的协调配合，能够发挥各储能介质优势的同时，减少蓄电池的充放电次数，提高蓄电池的寿命，增强系统的实时平抑风电波动的能力。

以成本最小为目标函数，建立混合储能的数学模型；采用多种群遗传算法，有效解决了传统遗传算法可能出现早熟，容易收敛到局部最优解的问题，得到更优的混合储能容量PSCrated=2.87MW、PBatrated=4.95MW、QSCrated=13.63kWh、QBatrated=1710.61kWh。

[1] SORENSEN P.CUTULULIS N A,VIGUERASRODRIGUEZ A,et al.Power fluctuation from large wind farms[J].IEEE Trans on Power Systems,2007,22(3);958-965.

[2] 汪海蛟与江全元,应用于平抑风电功率波动的储能系统控制与配置综述[J].电力系统自动化,2014(19):126-135.

[3] Rasmussen C N．Energy storage for improvement of wind power characteristics [C] //IEEE Trondheim Power Technology．Trondheim，Norway：IEEE，2011：1-8．

[4] 国家电网公司“电网新技术前景研究”项目咨询组.大规模储能技术在电力系统中的应用前景分析[J].电力系统自动化，2013，37(1)；3-8.Consulting Group of State Grid Cooperation of China to Prospects of New Technologies in Power Systems.An analysis Prospects of application of large-scale energy storage technology in power systems[J].Automation of Electric Power Systems,2013,37(1);3-8.

[5] 赵艳雷，李海东，张磊，等.基于快速储能的风电潮流优化控制系统[J].中国电机工程学报,2013,13(3)：6，+47-54.

[6] 孟润泉，刘家赢，文波,等.直流微网混合储能控制及系统分层协调控制策略[J].高压电压技术，2015(7)：108-115.

[7] 张国驹，唐西胜，齐智平.平抑间歇式电源功率波动的混合储能系统设计[J].电力自动化，2011(20)：29-33，+98.

[8] 文波，秦文萍，韩肖清，等.基于电压下垂法的直流微电网混合储能系统控制策略[J].电网技术，2015(4)：19-25.

[9] ABBEY C，STRUNZ K，JOOS G，A knowledge-based approach for control of two-level energy storage for wind energy systems[J].IEEE Trans on Energy Conversion，2009，24(2);539-547.

[10] 邹见效，戴碧蓉，彭超,等.基于荷电状态分级优化的混合储能风电功率平抑方法[J].电力系统自动化，2013(24)：7-12.

[11] 谢石骁，杨莉，李丽娜.基于机会约束规划的混合储能优化配置方法[J].电网技术，2012(5)：85-90.

[12] PAATERO J V,LUND P D.Effect of energy storage on variation in wind power[J].Wind Energy,2005,8(4)；421-441.

[13] 李成，杨秀，张美霞，等.基于成本分析的超级电容器和蓄电池混合储能优化配置方案[J].电力系统自动化，2013(18)：26-30.

[14] 杨珺，张建成，桂勋.并网风光发电中混合储能系统容量优化配置[J].电网技术，2013(5)：30-37.

[15] 张坤，毛承雄，谢俊文，等.风电场复合储能系统容量配置的优化设计[J].中国电机工程学报，2012(25)：13，+106-114.