海底声散射特性研究进展
刘保华,阚光明,裴彦良,杨志国,于凯本,于盛齐
(1.国家深海基地管理中心,山东 青岛 266061;2.青岛海洋科学与技术国家实验室 海洋地质过程与环境功能实验室,山东 青岛 266237;3.国家海洋局第一海洋研究所 海洋沉积与环境地质国家海洋局重点实验室,山东 青岛 266237)
海底声散射特性研究进展
刘保华1,2,阚光明2,3*,裴彦良2,3,杨志国1,于凯本1,2,于盛齐1
(1.国家深海基地管理中心,山东 青岛 266061;2.青岛海洋科学与技术国家实验室 海洋地质过程与环境功能实验室,山东 青岛 266237;3.国家海洋局第一海洋研究所 海洋沉积与环境地质国家海洋局重点实验室,山东 青岛 266237)
海底是水下声场的重要边界,其声散射特性对水下声场空间结构及分布规律具有至关重要的影响。对目前国际上海底声散射特性研究方面的进展进行了系统的分析和总结,从海底声散射测量技术、海底声散射特性及机理、海底声散射预测模型3个方面进行了论述,并提出了未来研究的方向、研究重点与难点。该工作对于充分了解和认识海底声散射研究的目前现状和未来发展趋势具有很好的借鉴和指导意义。
海底声散射特性;散射模型;海底混响;水下声场
1 引言
水下声场空间结构及分布规律研究在水下目标探测、水下通讯和导航、水文测量和海底地形地貌勘测等军事、海洋科学及生产领域具有重要的应用价值。海底是水下声场的一个重要边界,包括海底声散射特性在内的海底声学特性对水下声场的空间结构和分布规律具有至关重要的影响。海底声散射是海洋混响的重要来源,而海洋混响则是主动声呐探测的主要干扰源。因此,研究海底声散射有利于包括海底混响在内的海洋混响的准确预报,对于提高水下声呐性能和目标探测的精度具有重要意义。另外,海底声散射研究还与浅海声场预报、匹配场定位、潜艇着底隐蔽地点选择等应用具有密切的关系。
海底声散射特性与海底粗糙度、沉积物非均匀性以及声波掠射角密切相关,对于不同的测量频率,其相关性变化规律也不相同。而且,不同的海底环境条件以及不同的声波频率,其声散射机理也不相同。因此,深入认识海底声散射特性、影响机理以及预测模型,是进行水下声场空间结构研究、水下声场准确预报和水下目标精确探测的重要环节。鉴于海底声散射特性的重要性,早在20世纪50年代,国外科学家就开始了海底声散射特性的测量和研究[1]。之后,不同研究者分别从测量技术、特性及机理分析、预测模型等方面开展了大量的研究工作。与国外相比,目前国内无论是在海底声散射测量技术还是在散射机理和模型等方面开展的研究还非常少,存在很大的差距。
本文对目前国际上海底声散射特性测量技术及机理和预测模型方面的研究成果进行了总结,阐述了国际上在海底声散射测量技术研发、海底声散射特性测量及机理分析、海底声散射预测模型研究等方面的发展现状,并提出了目前研究工作中尚未解决的问题及未来研究的方向、研究重点与难点,以期能够对我国将来海底声散射特性的研究工作提供借鉴和指导。
2 海底声散射特性测量技术研究进展
美国海底声散射测量开始于20世纪50年代。Urick[1]将一收发合置的圆柱活塞换能器固定在木杆上,借助于驳船将换能器放置在靠近海底处,进行了最早期的海底反向散射测量。测量的频率范围为10~60 kHz,通过水平和垂直方向旋转木杆,来获得不同方位角和掠射角的测量数据。Urick和Saling[2]又采用炸药声源对水深为4 400 m的海底进行了反向散射测量,声源的频带约为500~8 000 kHz,炸药的爆炸深度和水听器沉放深度均为15 m。Wong和Chestermax[3]采用一个磁致伸缩的换能器作为声源和接收水听器,在香港的近岸海域进行了海底的反向散射测量,测量的频率为48 kHz,发射声波的脉冲宽度为0.4 ms和2.8 ms两种。总之,在20世纪50-60年代,海底声散射测量刚刚起步,实验所使用的均是非常简单的装置,还未开展专业的海底声散射测量技术研究。
20世纪70年代末,美国华盛顿大学应用物理实验室的Barry等[4—5]研制出一种拖曳式海底反向声散射测量装置(图1)。通过一个类似于球状万向节(ball-in-socket)的调节机构,将发射和接收合置的声学换能器安装在拖曳平台上,调节机构可以方便实现换能器掠射角的调整,平台上还安装由测深和姿态传感器。Jackson等[6]采用该设备对粉砂、砂质和砾石海底度进行了反向声散射测量,通过安装3个不同频带的收发合置平面换能器获得了20~85 kHz的频带覆盖范围,换能器垂直方向发射和接收波束角为20°~40°,水平波束角为10°~20°,声源级为205 dB re.μPa@1 m,实验中平台的拖曳速度为2~5 kn。Stanic等[7]研制出一种适用于浅水的坐底式海底声散射系统(图2),整套系统由两个坐底式的塔式支架组成,两个支架安装由16个水听器组成的T型接收阵,其中一个还安装有高频参量阵声源,声源的差频频率为20~180 kHz,差频声源级为187 dB re.μPa@20 kHz和214 dB re.μPa@180 kHz,该系统可进行高频的海底反向声散射和前向声散射测量。除上述两套海底声散射测量设备外,Boehme等[8]将发射和接收换能器安装在一个高4 m的三角架上,将该装置放置在海底进行了频率范围为30~95 kHz的海底反向声声散射测量。从上述的分析可以看出,在20世纪70-80年代,海底声散射测量技术得到快速发展,研发出了多台套的专门用于海底声散射测量的专业设备,测量精度得到很大提高。本阶段的测量频率主要集中在20 kHz以上的高频。
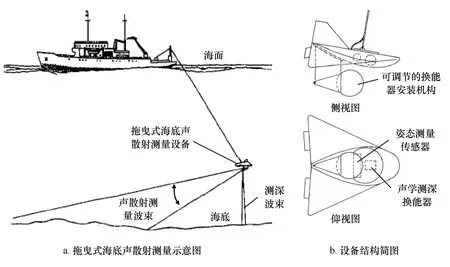
图1 Barry等研发的拖曳式海底声散射测量装置(改自文献[5-6])Fig.1 Towed sonar system for bottom scattering measurement(modified from reference[5-6])
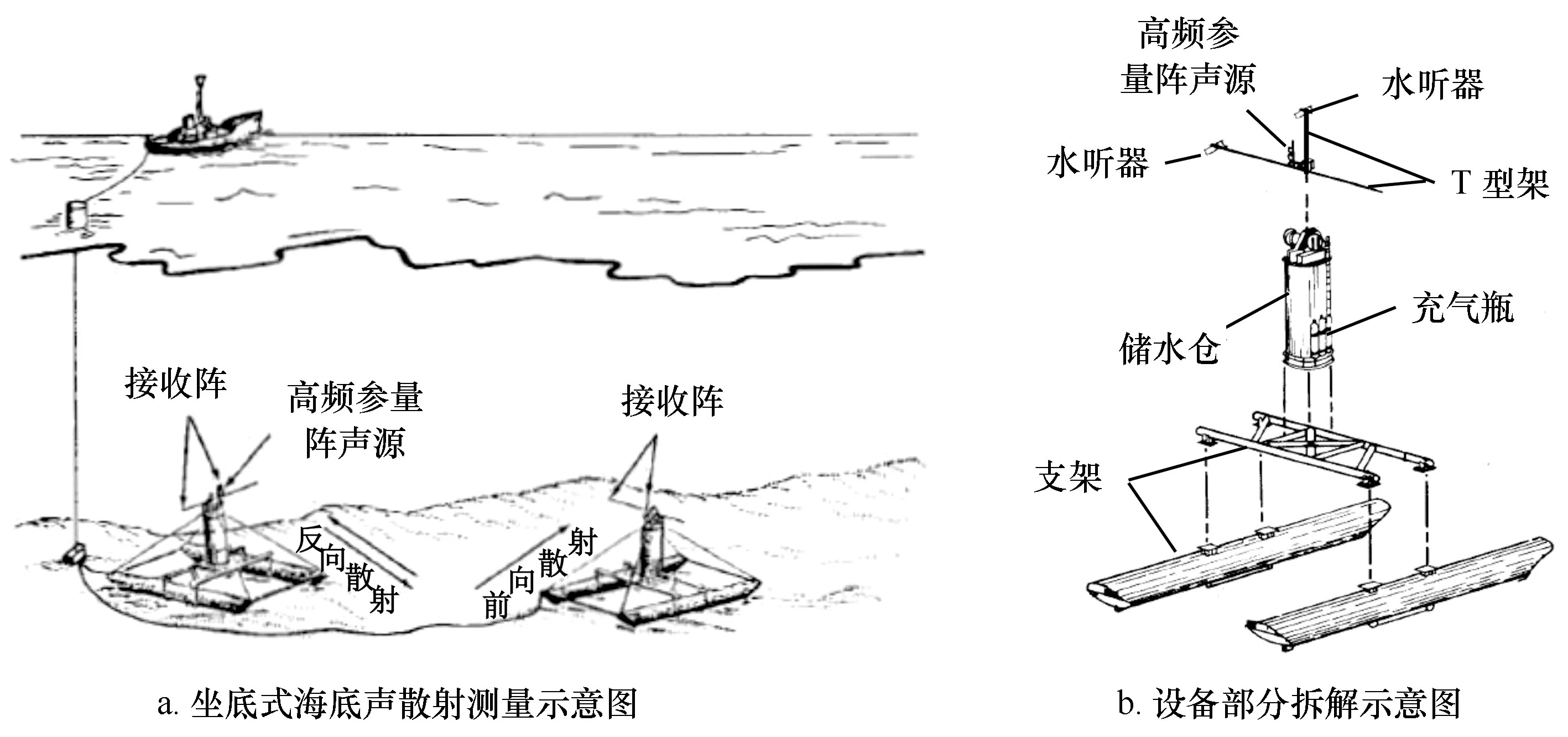
图2 Stanic等研发的坐底式海底声散射测量系统(改自文献[7])Fig.2 Bottom-mounted bottom scattering measurement system(modified from reference[7])
20世纪90年代中,Greaves和Stephen[9]采用由10个低频弯张换能器组成的垂直线阵声源和由128个水听器组成的水平接收阵在大西洋中脊进行了海底声散射测量。垂直线阵声源的弯张换能器的排放间距为2.29 m,通过各换能器的时延相控发射,声源可以形成俯角为9°的相控波束,在实验中,声源进行LMF扫频发射,扫频宽度为200~255 Hz,信号长度为5 s。接收阵列的基元间距为2.5 m,通过波束形成技术,产生了126个具有不同方向的接收波束,但0°~30°和150°~180°两个波束方向的数据因波束太宽且受接收阵姿态变化和船舶噪音的影响大而无法使用[9]。20世纪90年代末和21世纪初,美国海军研究办公室联合华盛顿大学、Scripps海洋研究所、意大利NATOSACLANT海底科学研究中心等科研机构开展了两个综合的海底声学实验,分别为:SAX99(Sediment Acoustic Experiment-1999)和SAX04(Sediment Acoustic Experiment-2004)[10—12]。在SAX99实验中采用了BAMS(Benthic Acoustic Measurement System)、STMS(Sediment Transmission Measurement System)、XBAMS(Accelerated Benthic Acoustic Measurement System)3种系统进行海底声散射测量[10-11]。BAM系统的工作频率为40 kHz和300 kHz,XBAMS的工作频率为300 kHz,二者的换能器均可以按一定的波束角在水平方向上步进旋转,以获得不同方位角的海底声散射强度(图3)。STMS为一个可用于海底沉积物声衰减测量、海底声透射和海底声散射测量的综合测量系统,其海底声散射测量的工作频率为20~150 kHz,换能器不能够自动旋转,需要潜水员通过移动设备来进行不同区域的海底散射测量。SAX04项目使用的设备类似于STMS的固定式换能器,但较SAX99具有如下两点改进:(1)测量频带拓宽为20~500 kHz;(2)将声学测量设备安装在一个长约28 m的铺设在海底的导轨上,声学测量设备在导轨上按照指定步长自动移动,以减少潜水员人工移动设备对测量产生的影响[11]。纵观20世纪90年代的海底声散射测量技术发展,主要有如下两个特点:(1)新技术不断被应用到海底声散射测量,如:低频弯张换能器技术,时延相控发射技术,多基元接收波束形成技术,步进自动控制技术等;(2)同步开展海底粗糙度、沉积物非均匀性等环境参数测量以及相关技术研发,以便能够建立精细的海底声散射预测模型。
进入21世纪,海底声散射测量及相关技术研发在很多国家得到广泛重视。2000年,意大利SACLANT海底研究中心的Holland等[12]采用如图4所示垂直接收阵和组合换能器声源对400~4 000 Hz频带范围内的海底反向声散射进行了测量。实验采用的ITC4001换能器声源由3个换能器组成,通过不同组合间隔产生频率分别为1 200 Hz、1 800 Hz、3 600 Hz的指向性声波,弯张换能器声源由两个间距为1.25 m的低频弯张换能器组合产生频率为600 Hz的指向性声波。接收采用间距为18 cm的32基元垂直接收阵。加拿大国防研究发展中心的Hines等[13]研发了一种用于浅海中频小掠射角海底声散射测量的设备,对频率为4 kHz和8 kHz、掠射角为3°~15°的砂质海底反向声散射特性进行了测量。系统主要由参量阵声源、超指向性线列阵、声强立体接收阵、安装平台等部分组成(图5)。参量阵声源由9个基元组成,4 kHz和8 kHz的发射响应分别为185 dB和192 dB(测量距离为5 m),水平和垂直波束宽度为4°~7°。超指向性接收阵由6个小型全向性水听器组成,基元间距为16 cm。安装参量阵和超指向性线列阵的支架可以360°旋转,水平和垂直转角的测量精度为±1°。2010年,韩国汉阳大学的La和Choi采用单个的全向性声源和全向性水听器在韩国南部的近岸浅水海域开展了频率为8 kHz的海底声散射测量[14]。Manik等[15]使用定量回声测深仪进行了海底反向散射测量。近几年的海底声散射测量的显著特点是:研究人员将研究重点转向了10 kHz以下的中低频海底声散射的测量和研究,主要原因在于中低频声呐在水声通讯、水下探测等方面的广泛应用。
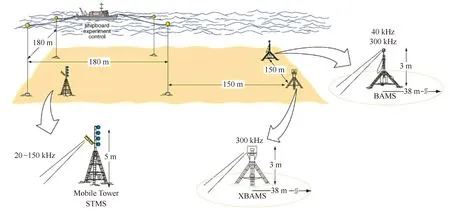
图3 SAX99实验海底声散射测量观测系统示意图(改自文献[11])Fig.3 Geometry of bottom scattering in SAX99(modified from reference[11])
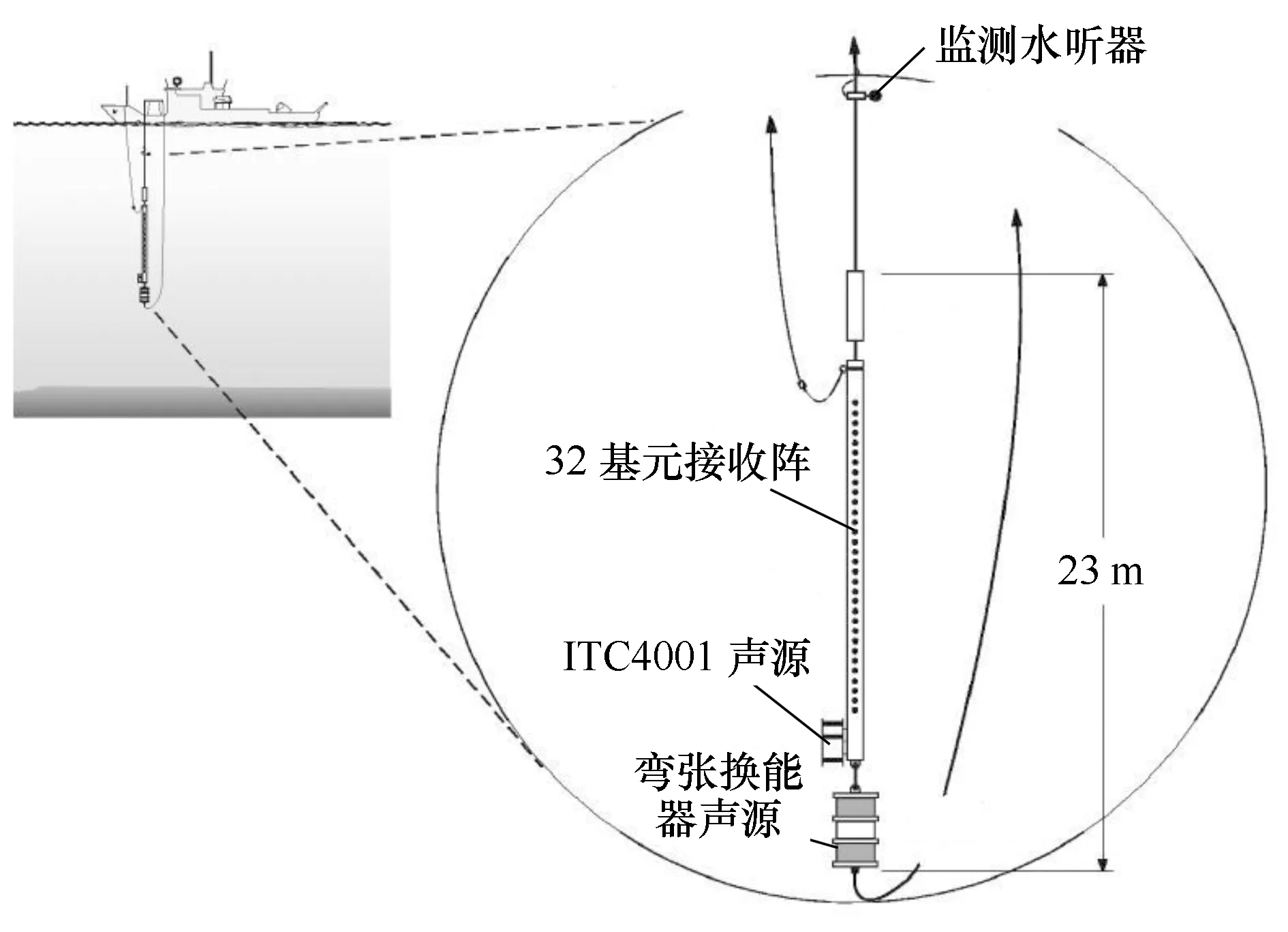
图4 中低频(400~4 000 Hz)海底声散射测量装置(改自文献[12])Fig.4 The device used for bottom scattering measurement at low-mid frequency(400-4 000 Hz) (modified from ref-erence[12])

图5 浅海小掠射角海底反向散射测量实验(改自文献[13])Fig.5 Geometry of bottom backscattering at low grazing angle in shallow water(modified from reference[13])
在国内,金国亮等[16]在放置于海底的支架上安装10个换能器,轮流以其中一个作为发射,其余作为接收,进行了频率为10 kHz的海底声散射测量[16]。近几年,宋磊[17]和薛婷[18]研究了采用具有指向性平面换能器和T型接收阵进行海底散射系数的实验测量方法,并在浅海进行了初步的实验测量。曹正良等[19]采用T矩阵方法对平面海底界面上球体目标的声散射建模进行了研究。总体来说,国内目前还没有用于海底声散射测量的专业设备,研究主要集中于理论分析和数值仿真。
3 海底声散射特性及机理研究进展
20世纪50-60年代,海底声散射特性研究主要是分析海底反向声散射与掠射角、声波频率、发射脉冲长度、海底底质类型等参数的关系[1—3,20]。主要结论如下:(1)海底声散射总体上随着掠射角的增大而增加,但对于不同的海底类型和掠射角范围,二者的函数关系则不同;(2)绝大部分研究人员认为海底声散射强度不存在明显的频率依赖性,或仅存在很弱的频率依赖性;(3)海底声散射强度与发射脉冲长度不存在明显的相关性;(4)虽然散射强度与海底沉积物颗粒粒径不存在明显变化规律,但对于不同类型的海底,声散射强度还是存在一些普遍的趋势,即:砂质和岩石等硬质海底声散射强度一般大于黏土和粉砂等软质海底的声散射强度。在声散射机理方面,研究人员得出一些初步的认识,普遍认为海底声散射主要是由海底的粗糙度或微起伏所引起的。但对于海底沉积物颗粒对声散射的贡献,不同研究者给出了不同的结论。Urick[1]认为海底声散射主要由海底粗糙性(即不规则性)引起,而不是沉积物颗粒对声波的散射。Wong和Chestermax[3]则指出,对于48 kHz的声波,砂质或更大粒径的颗粒是小掠射角时海底声散射的主要散射体,在较大掠射角和近垂直入射时,海底粗糙散射是主要机制。McKinney和Anderson[20]指出沉积物的颗粒属性也是引起海底声散射的一个重要方面,但颗粒和粗糙性并不是相互独立的两个方面,沉积物颗粒堆积在一起形成与声波波长尺寸相当的散射体,这是海底散射与颗粒具有一定相关性的原因;另一方面,这些颗粒堆积体也正是形成海底微起伏(即粗糙性)或沉积层结构的重要因素。除此之外,Urick和Saling[2]基于中低频(500~8 000 Hz)声散射数据指出海底沉积物中沉积层反射可能是引起海底声散射增加的一个因素。
20世纪70-80年代,海底声散射测量主要集中在浅海(水深小于50 m)和高频(20~180 kHz)反向声散射测量,海底底质包括淤泥、粉砂、细砂、含贝壳层、砾石和岩石等多种类型。此时期主要的研究进展如下:(1)海底声散射强度随掠射角的增大而增强,二者关系可以采用Lambert法则公式较好地拟合,即:BS=10lgμ+10lg(sin2θ),θ为掠射角,10lgμ为垂直入射时的声散射[21—24];(2)声散射存在微弱的频率依赖性,但不同研究者依据不同的底质类型和测量频率分别给出了不同的变化关系,总体来说,声散射与声波频率的关系很难用一个简单的函数来表述,其与海底底质类型、海底粗糙度、测量频率等多个参数有关[6,21—24];(3)开展了声散射强度与方位角关系的研究,Stanic等[22—23]在Panama城附近海域的砂质海底和Jacksonville附近海域的含有粗贝壳层海底的测量数据均未显示出明显的方位角依赖性,而Boehme等[21]通过在水平方向上以不同的方位角扫描具有良好分界的细砂和粗砂海底,发现了在分界线处海底散射强度的明显变化;(4)在开展海底声散射测量的同时,采用侧扫声呐、水下摄像、立体照相、高分辨率测深、浅地层剖面、沉积物岩心分析等技术对海底粗糙性和非均匀性等底质环境进行了测量,为深入研究散射机理和模型奠定了基础[21];(5)虽然海底粗糙性是引起海底声散射的主要机制,但多个海区的数据表明海底散射强度与均方根高度没有明显的相关关系,这说明对于海底声散射来说海底均方根粗糙度不是海底粗糙性的有效表述参数,研究者开始采用海底粗糙度谱来表征海底粗糙度[23]。在海底声散射机理研究方面,在目前研究的频率范围内(20~180 kHz),颗粒散射不是海底声散射的主要机制,这一点得到普遍共识。Jackson等[6]综合多种数据指出,对于颗粒粒径大小相似的海底散射强度相差10~15 dB。研究人员普遍认为,海底粗糙散射和体积散射是海底散射的主要机制,但对于两种散射机制对海底声散射的贡献程度及适用条件,不同研究研究人员给出了不同的结论:Bunchuk和Zhitkovskii[24]认为在浅水区主要是体积非均匀性而不是界面粗糙性来主导海底声散射;而Jackson等[25]则认为,对于淤泥和粉砂等软质海底,在除了很小和很大掠射角之外的中等掠射角范围内,体积散射占主导作用,而对于粗砂等硬质海底,在很宽的掠射角范围内粗糙散射均占主导地位。Jackson等开发了包括粗糙散射和体积散射在内的复合粗糙度散射模型,但该模型并未给出体积散射强度的计算公式,而是采用一个自由变量来代替,需通过数据拟合来确定[25]。如何能够更好地揭示粗糙散射和体积散射两种机制,则需要更完善的模型以及更多的声学和底质参数测量数据。
20世纪90年代,海底声散射特性测量和研究具有如下进展和特点:(1)除传统的高频(20~300 kHz)测量外,研究人员对1 000 Hz以下的低频海底声散射特性进行了测量和散射机理研究:Tang等[26]采用频率为250~650 Hz的深拖地震技术测量了大西洋中脊附近沉积物盆地的海底声散射特性;Greaves和Stephen[9]采用200~255 Hz的声波对大西洋中脊地壳特征进行了测量,试图建立声散射强度与地壳倾角的相关关系以便能够采用声散射数据来识别具有不同倾角的地壳类型,但未能给出满意的结果。(2)测量和研究了海底浅表层沉积物中存在的气泡所引起的声散射特性及模型:Tang等[27]对比了砂质海底与含气泡层的粉砂海底的声散射特性,指出砂质海底的声散射主要是由海底界面散射引起,而粉砂海底声散射主要由浅表层沉积物中的气泡对声波的散射引起;Chu等[28]进一步建立了一个双层的模型来模拟由海底气泡引起的双基地散射强度,模型假设气泡为扁圆球形,且不同气泡散射不存在相干性,均为一次散射。(3)开展了高频的收发分置的双基地海底声散射的测量和研究:Stanic等[29]采用如图2所示装置测量了频率为20~180 kHz的海底双基地散射特性;Williams和Jackson[30]分别测量了频率为40 kHz的粗砂海底和含气的粉砂海底前向散射强度,并将测量数据与基于反向散射模型推导出的前向散射模型的预测结果进行了对比。(4)SAX99和SAX04综合声学实验开始实施,实验的最大特点是同步开展了精细的海底环境特性测量和精确的高频海底声散射同步测量,对海底粗糙度和沉积物非均匀性特征进行了详细测量和表征,为高频海底声散射特征及声散射模型综合研究提供了大量的基础数据[10—11,31—32]。在声散射机理研究方面,除海底粗糙界面引起的声散射之外,研究者开始关注海底之下沉积物特性引起的声散射,并给出了多种海底之下声散射的机制[25,27—28,33—35]。Jackson等建立的复合粗糙度散射模型虽然指出沉积物体积散射的存在,并没有分析引起沉积物体积散射的具体机制[25];Hines认为海底沉积物孔隙度的波动是引起体积散射的重要机制[33];Lyons等[34]将海底之下声散射归结为两种机制:一是与Hine提出的孔隙度波动相类似的沉积物的非均匀性,另一种是海底沉积物层引起的粗糙界面声散射;Tang等[27]和Chu等[28]认为,对于浅表层沉积物含气泡的粉砂质海底,气泡对声波的散射是海底散射的主要机制;Jackson和Ivakin[35]认为除了密度和纵波速度(声速)非均匀性之外,剪切波速度非均匀性也是引起体积散射的主要因素。总之,到目前为止,研究人员普遍认识到海底散射主要由海底界面散射和来自海底沉积物的声散射组成。海底的粗糙性是引起界面散射的主要机制,可采用海底粗糙度谱来表征海底的粗糙性。海底沉积物的声散射来源于多种机制,包括由海底沉积物非均匀性(密度、孔隙度、声速、剪切波速度等非均匀性)引起的体积散射、海底气泡引起的声散射、海底沉积物层(或基底)粗糙性引起的声散射、非连续沉积层引起的体积散射等。因此,在进行海底声散射特性研究时,应针对不同的声波频率和特定的海底环境条件,认真分析引起声散射的机制,以便更好地对声散射特性进行建模。
21世纪以来,中低频的海底声散射特性测量和研究获得广泛关注。Holland等[12]采用图4所示的方法分别在泥质和岩浆岩海底测量了频率为400~4 000 Hz的海底反向散射强度,掠射角为10°~40°。测量结果表明,在该频段内岩浆岩海底的散射强度均大于泥质海底。机理分析认为,泥质海底声散射主要来自于海底之下沉积层的体积散射,而海底界面散射非常小;岩浆岩海底声散射在低于临界掠射角时为海底界面散射,大于临界掠射角时主要为体积散射。Soukup和Gragg[36]采用由全向性换能器组成的线性声源阵和9基元垂直接收阵对石灰岩海底进行了频率为2~3.5 kHz的海底反向声散射测量,并分析了此频率段内海底反向声散射强度与掠射角的关系。Hines等[13]采用如图5所示装置在两个砂质海底站位测量了频率为4 kHz和8 kHz的海底反向散射,掠射角为3°~15°。总体来说,目前中低频海底声散射特性测量逐步开始,但其散射机理及预测模型还未开展系统性的研究。
4 海底声散射模型研究进展
4.1 Lambert模型
Lambert模型(或称为Lambert定律)能够很好地描述粗糙面上反向散射强度以及在相对光滑界面上(组成界面的小散射体的几何尺度远小于入射声波波长)较小掠射角情况下的反向散射强度与掠射角的关系[37]。但是,Lambert定律是半经验公式,缺乏具体的物理含义,而且,Lambert定律仅仅描述了散射强度与掠射角的关系,与海底粗糙度参数无关。通过该定律只能获得入射声线、散射声线及散射面法线位于同一平面时的散射强度。Ellis[38],Caruthers和Novarini[39]对Lambert定律进行改进,给出了一种与Lambert定律类似的三维散射强度计算模型。
4.2 基尔霍夫(Kirchhoff)近似模型
基尔霍夫近似模型适合粗糙界面起伏变化比较缓慢的情况(Rc≫λ/πsin3θ,Rc为界面的曲率半径,λ和θ为入射波局部掠射角和波长),而对海底起伏高度和界面斜率没有要求。Echart最早将基尔霍夫近似用于海面的声散射研究,Jackson等[25]将基尔霍夫近似用于镜面反射方向附近的频率为10~100 kHz的海底声散射的计算,并将近垂直的方向散射测量数据与基尔霍夫模型预测进行了对比。Moustier[40]将基尔霍夫近似应用于多波束数据的近垂直入射时声散射与海底底质属性关系的研究。Dacol[41]曾将基尔霍夫近似用于具有随机粗糙特性的弹性海底的声散射研究。Williams和Jacson[30]将基尔霍夫近似用于收发分置的双基地散射模型的研究。对于高频声散射,Jackson和Richardson[42]等给出了高频极限条件下的基尔霍夫近似的散射截面表达式。基尔霍夫近似中未考虑影区效应和多次散射,目前基尔霍夫近似主要用于倾角变化缓慢的粗糙海底近垂直方向附近的海底声散射场的计算。
4.3 小粗糙度微扰近似模型
微扰近似理论适用于粗糙界面起伏很小(小于入射波波波长)且界面斜率足够小的情况,因此称为小粗糙度微扰近似模型。微扰理论认为当粗糙界面起伏比较小时,它对声场的影响比较小,可以将声场看成由光滑界面产生的场和一个扰动散射场叠加组成。小粗糙度微扰近似是在海底声散射场计算中得到广泛应用的模型,根据导出散射截面表达式时所基于的波动方程类型的不同,又可以分为小粗糙度微扰近似流体模型、小粗糙度微扰近似弹性模型以及小粗糙度微扰近似多孔弹性模型。Kuo[43]给出了无损耗流体沉积物情况下的小粗糙度微扰流体近似模型表达式,Jackson和Briggs[44]将表达式推广到有限衰减的情况,并将模型预测与砂和粉砂等不同类型的海底声散射测量数据进行了对比,但该模型假设沉积物各向同性,且不存在任何形式的分层或梯度。后来,Moe和Jackson[45]将微扰流体模型应用于具有声速梯度的海底,给出了此种情况下的海底声散射强度和散射截面的一般表达式。Kuperman等研究人员将微扰流体模型扩展至分层海底的情况,并将剪切效应纳入到海底声散射的研究,建立了各向同性小粗糙度微扰近似弹性模型,用于弹性海底声散射的研究[46—48]。实际海底是由流体和固体骨架组成的两相多孔弹性介质,Williams等[49]将Biot模型与小粗糙度微扰近似相结合来研究海底声散射问题,建立了小粗糙度微扰多孔弹性模型。Jackson和Richardson[42]对该模型运算进行了改进,采用矩阵方法来表示散射截面,从而降低代数运算的复杂性。
4.4 小斜率近似模型
小斜率近似模型最早为研究海面声散射而建立的,后来被广泛应用于海底声散射的研究,其表达式是关于界面斜率的一系列展开式[50—52]。普遍认为,小斜率近似比小粗糙度微扰近似和基尔霍夫近似更为精确,且一种近似方法几乎可以涵盖几乎所有的掠射角范围(基尔霍夫近似适合镜像反射方向附近的散射,小粗糙度微扰近似适合镜像反射附近之外的散射)。Broschat和Thorsos[53]详细推导了适合Dirichlet边界条件的粗糙界面小斜率近似模型的散射截面表达式,并详细研究了小斜率近似用于海底声散射计算时的精度,小斜率近似的精度与界面均方根倾角、界面相关长度和入射角有关。目前,小斜率近似模型是应用最广泛的海底声散射模型。Gragg等[54]采用小斜率近似模型研究包含均匀散射体的随机粗糙海底的声散射,推导出此种条件下的双基地散射公式。Soukup等[55],Jackson[56]将小斜率近似应用于包含剪切效应的弹性海底声散射的研究,Jackson将其推广到层状海底声散射研究。
4.5 复合粗糙度近似模型
复合粗糙度近似模型的核心思想是将海底粗糙度划分为大尺度和小尺度两部分,充分利用基尔霍夫近似和小粗糙度微扰近似在适用条件上的互补性,对于大尺度粗糙度采用基尔霍夫近似计算海底散射,对于小尺度粗糙度采用小粗糙度微扰近似。早期主要用于海面声散射的研究,后来被Jackson应用于海底声散射研究,其将垂直入射附近的大尺度粗糙度采用基尔霍夫近似计算海底散射,小粗糙度采用微扰近似计算海底散射[23]。复合粗糙度近似模型的问题在于用于区分大小尺度粗糙的截止波数的选择很难十分清楚地确定,一般通过多次的试算和比较来确定。Thorsos[57]指出,对于小掠射角的声散射计算,复合粗糙度近似模型的精度偏低。研究人员在早期的海底声散射模型研究中采用复合粗糙度模型,目前复合粗糙度模型逐渐被小斜率近似模型代替。
4.6 其他模型
针对具有分层的海底中低频声散射,Jackson等[58]建立了GABIM模型。GABIM模型将海底视为多层的流体,综合运用基尔霍夫近似、一阶微扰近似和经验公式来计算海底界面粗糙散射,采用一阶微扰近似和经验公式来计算体积散射,该模型对100~10 000 Hz的中频声波海底散射强度具有较好的预测效果。国内研究人员在海底声散射和海底混响计算方法和模型方面也开展了卓有成效的研究,张仁和和金国亮[59],李风华等[60]采用简正波理论对浅海环境下的混响特性进行了研究。彭朝晖等[61]结合Ivankin等提出的射线管积分法和Hines的复射线法,推导出了一种计算随机非均匀海底和粗糙界面引起的平面内海底散射模型,此模型中考虑了折射波和衰减波的贡献。
5 发展趋势及研究难点
5.1 海底中低频声散射测量及模型研究
从上述分析来看,国内外对于海底声散射特性研究主要集中在大于10 kHz的高频段,而对频率小于10 kHz的中低频声散射研究相对较少,目前所开展的相关测量也只是局限在中频段的几个离散频率点,缺少系统性。中低频声散射研究可以弥补目前海底声散射研究在频段上的局限性。而且,中低频声波在海洋声场测量与预报、海底埋藏物声学探测、水声通讯以及海洋地球物理探测等领域具有重要的应用价值。海底中低频声散射的系统性测量以及相关模型研究已成为海底声散射研究发展的趋势和研究热点。相对于高频声散射而言,海底中低频声散射无论是声散射特性测量,还是散射机理分析和预测模型研究,均更为复杂。测量的复杂性在于常规中频换能器声源的指向性差,易受海面声散射的干扰,影响测量精度;散射机理和模型的复杂性在于其可能同时受海底粗糙界面散射和沉积物内非均匀体散射的共同作用,从而导致其预测模型更为复杂。研发声学参量阵等中低频高指向性声源和多基元接收阵列是解决中低频声散射精确测量的途径之一。在机理分析方面,与中低频声散射相匹配的海底粗糙度和海底非均匀等参数的测量和表征是一个很大的挑战,也是今后需要重点解决的难点之一。而且,海底中低频声散射受海底粗糙面散射、海底体积散射、海底沉积层散射等多种机制共同作用,彻底弄清各种机理及其对声散射的影响和贡献,也是今后海底声散射机理研究的难点和需要重点关注的研究课题。在中低频模型研究方面,需要重点解决经过高频声散射数据验证了的高频声散射模型在中低频段的适用性问题,通过数据和模型对比,研究建立适合中低频海底声散射特性预测的地声模型。
5.2 小掠射角和各向异性粗糙海底等特殊条件下的声散射特性研究
小掠射角(小于10°)声散射是引起远距离混响的重要因素,在远程声探测方面具有重要的应用价值,是在今后的研究中需要重点关注的研究课题。浅海小掠射角声散射测量的难点在于海面散射和多途声传播的影响。在散射机理研究方面,当声波以小于临界掠射角的小掠射角入射到海底时,有时在近海底沉积物中产生渐逝耗散波,这增加了小掠射角海底声散射机理的复杂性,也是小掠射角声散射研究的难点之一。在模型研究方面,目前常用的散射模型在小掠射角条件下的预测能力还未进行足够的测试,其适用性还有待研究。另外,目前海底声散射测量和研究往往将海底看成是统计意义上的各向同性粗糙海底,主要关注海底声散射随掠射角的变化。而当海底存在明显方向性的地貌特征时(比如方向性的海底沙波或方向性明显的海底冲刷沟槽等),海底粗糙度表现出明显的各向异性特征。由各向异性粗糙海底引起的声散射强度,不仅与掠射角有关,还与方位角有关。各向异性粗糙海底声散射测量和模型研究主要难点在于海底三维粗糙特性的测量和表征以及三维声散射场的精确测量,这将会成为未来发展的方向。
5.3 多层海底声散射模型研究
目前的海底散射模型一般将海底看作为未分层的半空间介质,而实际的海底沉积物中往往存在分层结构。在与海底相互作用过程中,声波往往透射进入海底界面之下(特别是对于中低频声波),被沉积物中的非均匀体和粗糙沉积层界面再次散射。采用更接近实际海底条件的多层声散射模型进行海底声散射特性预测将成为未来发展的趋势。虽然Jackson等在多层声散射模型方面开展了一些研究,但建立的GABIM模型将多层海底简化成流体模型,且模型的预测结果未进行实际数据的验证[58]。在多层海底散射模型方面今后还需要开展大量的针对实际海底情况的多层散射模型普适化和模型验证工作。多层海底声散射模型研究的难点一方面在于如何甄别海底界面粗糙散射、沉积物中体积散射、海底沉积层界面粗糙散射、沉积物声传播衰减等多种机制对散射总场的影响,另一方面是如何测量和表征海底以下多个沉积层界面粗糙度特性和界面之间沉积物的体积非均匀性。
5.4 双基地和前向声散射特性研究
目前国内外研究主要集中在收发合置(单基地)海底散射强度的测量和建模。相对于单基地声呐,双(多)基地声呐具有探测范围大、隐蔽性好、抗干扰能力强等优点。随着双(多)基地声纳的广泛应用,研究不同入射和散射掠射角以及不同入射和散射方位角时的海底双基地前向散射成为一种十分迫切的需要。研究人员在高频海底前向声散射测量方面做了一些尝试试验,但总体研究水平较低,特别是目前还没有开展中低频海底前向声散射测量。对于中低频前向声散射测量,研发满足测量要求的指向性声源和指向性接收换能器或接收阵列是需要解决的关键技术。对于浅海中低频前向海底声散射测量,如何避免海面声散射影响和声波的多途传播,是未来研究的难点。在散射模型研究方面,目前的海底声散射模型是否还适用于海底前向声散射特性的计算和预测,还需要开展大量的研究工作。
[1] Urick R J. The Backscattering of sound from a harbor bottom[J]. The Journal of the Acoustical Society of America, 1954, 26(2): 231-235.
[2] Urick R J, Saling D S. Backscattering of explosive sound from the deep-sea bed[J]. The Journal of the Acoustical Society of America, 1962, 34(6): 1721-1724.
[3] Wong H K, Chestermax W D. Bottom backscattering near grazing incidence in shallow water[J]. The Journal of the Acoustical Society of America, 1968, 44(6): 1713-1718.
[4] Barry W, Jackson D, Schultz J. A flexible towed sonar for ocean acoustic measurements[C]//Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Tulsa, OK, USA, 1978:152-154.
[5] Barry W A, Jackson D R. Split-beam towed sonar for ocean acoustic measurement[C]//OCEANS’80 Conference Proceedings, Seattle, WA, USA, 1980:267-271.
[6] Jackson D R, Baird A M, Crisp J J, et al. High-frequency bottom backscatter measurement in shallow water[J]. The Journal of the Acoustical Society of America, 1986, 80(4): 1188-1199.
[7] Stanic S, Eckstein B E, Williams R L, et al. A high-frequency shallow water acoustic measurement system[J]. IEEE Journal of Oceanic Engineering, 1988, 13(3): 155-161.
[8] Boehme H, Chotiros N P, Rolleigh L D, et al. Acoustic backscattering at low grazing angles from the ocean bottom. Part I. Bottom backscattering strength[J]. The Journal of the Acoustical Society of America, 1985, 77(3): 962-974.
[9] Greaves R J, Stephen R A. Seafloor acoustic backscattering from different geological provinces in the Atlantic Natural Laboratory[J]. The Journal of the Acoustical Society of America, 1997, 111(1): 193-208.
[10] Thorsos E I, William K L, Chotiros N P, et al. An overview of SAX99: acoustic measurements[J]. IEEE Journal of Oceanic Engineering, 2001, 26(1): 4-25.
[11] Williams K L, Jackson D R, Tang D J, et al. Acoustic backscattering from a sand and a sand/mud environment: experiments and data/model comparisons[J]. IEEE Journal of Oceanic Engineering, 2009, 34(4): 388-398.
[12] Holland C W, Hollett R, Troiano L. Measurement technique for bottom scattering in shallow water[J]. The Journal of the Acoustical Society of America, 2000, 108(3): 997-1011.
[13] Hines P C, Osler J C, MacDougald D J. Acoustic backscatter measurements form littoral seabeds at shallow grazing angles at 4 and 8 kHz[J]. The Journal of the Acoustical Society of America, 2005, 117(6): 3504-3516.
[14] La H, Choi J W. 8-kHz bottom backscattering measurements at low grazing angles in shallow water[J]. The Journal of the Acoustical Society of America, 2010, 127(4): 160-165.
[15] Manik H M, Furusawa M, Amakasu K. Measurement of sea bottom surface backscattering strength by quantitative echo sounder[J]. Fisheries Science, 2006, 72(3): 503-512.
[16] 金国亮, 吴承义, 张国华, 等. 浅海二维海底散射系数的测量[J]. 声学学报, 1987, 12(3):227-231.
Jin Guoliang, Wu Chengyi, Zhang Guohua, et al. The measurement of two-dimensional bottom backscattering coefficients at shallow water[J]. Acta Acustica, 1987, 12(3):227-231.
[17] 宋磊. 海底散射系数测量方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2007.
Song Lei. Study on measurement method of ocean bottom acoustic scattering coefficient[D]. Harbin: Harbin Engineering University, 2007.
[18] 薛婷. 基于T型乘积阵的海底散射系数测量方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
Xue Ting. Study on measurement method of ocean bottom acoustic scattering coefficient based on T-type multiplicative arrays[D]. Harbin: Harbin Engineering University, 2008.
[19] 曹正良,杜栓平,周士弘,等. 平面海底界面上球体目标的声散射建模研究[J]. 地球物理学报, 2010, 53(2): 401-410.
Cao Zhengliang, Du Shuanping, Zhou Shihong, et al. Modeling of acoustic scattering by sphere on a planar seabed[J]. Chinese Journal of Geophysics, 2010, 53(2): 401-410.
[20] McKinney C M, Anderson C D. Measurements of backscattering of sound from the ocean bottom[J]. The Journal of the Acoustical Society of America, 1964, 36(1): 158-163.
[21] Boehme H, Chotiros N P, Rolleigh L D, et al. Acoustic backscattering at low grazing angles from the ocean bottom. Part I. Bottom backscattering strength[J]. The Journal of the Acoustical Society of America, 1985, 77(3): 962-974.
[22] Stanic S, Briggs K B, Fleischer P, et al. Shallow-water high-frequency bottom scattering off Panama City, Florida[J]. The Journal of the Acoustical Society of America, 1988, 83(6): 2134-2144.
[23] Stanic S, Briggs K B, Fleischer P, et al. High-frequency acoustic backscattering from a coarse shell ocean bottom[J]. The Journal of the Acoustical Society of America, 1989, 85(1): 125-136.
[24] Bunchuk A V, Zhitkovskii Y Y. Sound scattering by the ocean bottom in shallow-water region(review)[J]. Soviet Physics Acoustics, 1980, 26:363-370.
[25] Jackson D R, Winebrenner D P, Ishimaru A. Application of the composite roughness model to high-frequency bottom backscattering[J]. The Journal of the Acoustical Society of America, 1986, 79(5): 1410-1422.
[26] Tang D J, Frisk G V, Sellers C J, et al. Low-frequency acoustic backscattering by volumetric inhomogeneities in deep-ocean sediments[J]. The Journal of the Acoustical Society of America, 1995, 98(1): 508-518.
[27] Tang D J, Jin G L, Jackson D R, et al. Analyses of high-frequency bottom and subbottom backscattering for two distinct shallow environments[J]. The Journal of the Acoustical Society of America, 1994, 96(5): 2930-2936.
[28] Chu D Z, Williams K L, Tang D J, et al. High-frequency bistatic scattering by sub-bottom gas bubbles[J]. The Journal of the Acoustical Society of America, 1997, 102(2): 806-814.
[29] Stanic S, Kennedy E, Ray R I. Variability of shallow-water bistatic bottom backscattering[J]. The Journal of the Acoustical Society of America, 1991, 90(1): 547-553.
[30] Williams K L, Jackson D R. Bistatic bottom scattering: Model, experiments, and model/data comparison[J]. The Journal of the Acoustical Society of America, 1998, 103(1): 169-181.
[31] Briggs K B, Tang D J, Williams K L. Characterization of interface roughness of rippled sand off fort Walton Beach, Florida[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 505-514.
[32] Wang C C, Hefner B T, Tang D J. Evaluation of laser scanning and stereo photography roughness measurement systems using a realistic model seabed surface[J]. IEEE Journal of Oceanic Engineering, 2009, 34(4): 466-475.
[33] Hines P C. Theoretical model of acoustic backscatter from a smooth seabed[J]. The Journal of the Acoustical Society of America, 1990, 88(1): 324-334.
[34] Lyons A P, Anderson A L, Dwan F S. Acoustic scattering from the seafloor∶modeling and data comparison[J]. The Journal of the Acoustical Society of America, 1994, 95(5): 2441-2451.
[35] Jackson D R, Ivakin A N. Scattering from elastic sea beds: First-order theory[J]. The Journal of the Acoustical Society of America, 1998, 103(1): 336-345.
[36] Soukup R J, Gragg R F. Backscatter from a limestone seafloor at 2-3.5 kHz: measurements and modeling[J]. The Journal of the Acoustical Society of America, 2003, 113(5): 2501-2514.
[37] 胡剑忠. 海底三维散射强度的测量和模型计算[D]. 哈尔滨: 哈尔滨工程大学, 2009.
Hu Jianzhong. Measurement and model calculation of sea bottom three-dimensional scattering strength[D]. Harbin: Harbin Engineering University, 2009.
[38] Ellis D D. Bistatic reverberation calculations using a three-dimensional scattering function[J]. The Journal of the Acoustical Society of America, 1991, 89(5): 2207-2214.
[39] Caruthers J W, Novarini J C. Modeling bistatic bottom scattering strength including a forward scatter lobe[J]. IEEE Journal of Oceanic Engineering, 1993, 18(2): 100-107.
[40] Moustier C D. Beyond bathymetry: mapping acoustic backscattering from the deep seafloor with sea beam[J]. The Journal of the Acoustical Society of America, 1986, 79(2): 316-331.
[41] Dacol D K. The kirchhoff approximation for acoustic scattering from a rough fluid-elastic solid interface[J]. The Journal of the Acoustical Society of America, 1990, 88(2): 978-983.
[42] Jackson D R, Richardson M D. High-frequency seafloor acoustics[M]. New York: Springer Science+Business Media, LLC, 2007.
[43] Kuo E Y. Wave scattering and transmission at irregular surfaces[J]. The Journal of the Acoustical Society of America, 1964, 36(11): 2135-2142.
[44] Jackson D R, Briggs K B. High-frequency bottom backscattering: roughness versus sediment volume scattering[J]. The Journal of the Acoustical Society of America, 1992, 92(2): 962-977.
[45] Moe J E, Jackson D R. First-order perturbation solution for rough surface scattering cross section including the effects of gradients[J]. The Journal of the Acoustical Society of America, 1994, 96(3): 1748-1754.
[46] Kuperman W A, Schmidt H. Rough surface elastic wave scattering in a horizontally stratified ocean[J]. The Journal of the Acoustical Society of America, 1986, 79(6): 1767-1977.
[47] Kuo E Y. Acoustic wave scattering from two solid boundary at the ocean bottom: reflection loss[J]. IEEE Journal of Oceanic Engineering, 1992, 17(1): 159-170.
[48] Essen H H. Scattering from a rough sedimental seafloor containing shear and layering[J]. The Journal of the Acoustical Society of America, 1994, 95(3): 1299-1310.
[49] Williams K L, Grochocinski J M, Jackson D R. Interface scattering by poroelastic seafloors: first-order theory[J]. The Journal of the Acoustical Society of America, 2001, 110(6): 2956-2963.
[50] Berman D H. Simulation of rough interface scattering[J]. The Journal of the Acoustical Society of America, 1991, 89(2): 623-636.
[51] Yang T Q, Broschat S L. Acoustic scattering from a fluid-elastic-solid interface using the small slope approximation[J]. The Journal of the Acoustical Society of America, 1994, 96(3): 1796-1804.
[52] Gragg R F, Wurmser D, Gauss R C. Small-slope scattering from rough elastic ocean floors: general theory and computational algorithm[J]. The Journal of the Acoustical Society of America, 2001, 110(6): 2878-2901.
[53] Broschat S L, Thorsos E I. An investigation of the small slope approximation for scattering from rough surface. Part Ⅱ. Numerical studies[J]. The Journal of the Acoustical Society of America, 1997, 101(5): 2615-2625.
[54] Gragg R F, Wurmser D, Gauss R C. Small-slope scattering from rough elastic ocean floors:General theory and computational algorithm[J]. The Journal of the Acoustical Society of America, 2001, 110(6): 2878-2901.
[55] Soukup R J, Canepa G, Simpson H J, et al. Small-slope simulation of acoustic backscatter from a physical model of an elastic ocean bottom[J]. The Journal of the Acoustical Society of America, 2007, 122(5): 2551-2559.
[56] Jackson D. The small-slope approximation for layered seabeds[J]. The Journal of the Acoustical Society of America, 2013, 133(5): 3251.
[57] Thorsos E I. Acoustic scattering from a “Pierson-Moskowitz” sea surface[J]. The Journal of the Acoustical Society of America, 1990, 88(1): 335-349.
[58] Jackson D R, Odom R I, Boyd M L, et al. A geoacoustic bottom interaction model(GABIM)[J]. IEEE Journal of Oceanic Engineering, 2010, 35(3): 603-617.
[59] 张仁和, 金国亮. 浅海平均混响的简正波理论[J]. 声学学报, 1984, 9(1): 12-20.
Zhang Renhe, Guo Jinliang. Normal-mode theory of the average reverberation intensity in shallow water[J]. Acta Acustica, 1984,9(1):12-20.
[60] 李风华,金国亮,张仁和. 浅海相干混响理论与混响强度的振荡现象[J]. 中国科学:A辑, 2000, 30(6):560-566.
Li Fenghua, Jin Guoliang, Zhang Renhe. Correlation reverberation theory in shallow water and oscillation phenomena of reverberation intensity [J]. Science in China (Series A), 2000,30(6):560-566.
[61] 彭朝晖,周纪浔,张仁和. 非均匀海底和粗糙度界面引起的平面内海底散射[J]. 中国科学:G辑, 2004, 34(4):378-391.
Peng Zhaohui, Zhou Jixun, Zhang Renhe. Bottom scattering in a plane from heterogeneous ocean bottom and rough interface[J]. Science in China (Series G), 2004, 34(4): 378-391.
A review on the progress of bottom acoustic scattering research
Liu Baohua1,2, Kan Guangming2,3, Pei Yanliang2,Yang Zhiguo1,Yu Kaiben1,2, Yu Shengqi1
(1.NationalDeepSeaCenter,StateOceanicAdministration,Qingdao266061,Chnia; 2.LaboratoryforMarineGeology,QingdaoNationalLaboratoryforMarineScienceandTechnology,Qingdao266237,China; 3.KeyLaboratoryofMarineSedimentologyandEnvironmentalGeology,TheFirstInstituteofOceanography,StateOceanicAdministration,Qingdao266237,China)
Seafloor is an important boundary for underwater sound field, and its acoustic scattering property has significant influence to spatial structure and distribution of underwater sound field. In this paper, we systematically analyzed and summarized the present progress on the measuring techniques, mechanism and modeling of bottom acoustic scattering property in the world. In addition, some research directions and topics which should be paid more attention to in the future were put forwarded as well as some research difficulties. This work will have great contribution to further studying and understanding the present status and the future trend of the research on bottom acoustic scattering property.
bottom acoustic scattering property; scattering model; bottom reverberation; underwater sound field
2016-08-04;
2016-12-12。
国家自然科学基金(41330965, 41527809);青岛海洋国家实验室开放基金(QNLM20160RP0209);海洋公益性科研专项资金项目(201405032);泰山学者工程专项经费项目(TSPD20161007)。
刘保华(1960-),男,山东省嘉祥县人,研究员,博士生导师,主要从事海洋地球物理研究。E-mail:bhliu@fio.org.cn
*通信作者:阚光明,男,副研究员,主要从事海底声学研究。E-mail:kgming135@fio.org.cn
10.3969/j.issn.0253-4193.2017.07.001
P733.23;P736.21
A
0253-4193(2017)07-0001-11
刘保华, 阚光明, 裴彦良, 等. 海底声散射特性研究进展[J]. 海洋学报, 2017, 39(7): 1-11,
Liu Baohua, Kan Guangming, Pei Yanliang, et al. A review on the progress of bottom acoustic scattering research[J]. Haiyang Xuebao, 2017, 39(7): 1-11, doi:10.3969/j.issn.0253-4193.2017.07.001

