海南岛莺歌海近岸的潮汐不对称与潮致余流研究
林国尧, 龚文平
(1.海南省海洋与渔业科学院,海南 海口570125;2.中山大学 海洋学院,广东 广州 510275)
海南岛莺歌海近岸的潮汐不对称与潮致余流研究
林国尧1, 龚文平2*
(1.海南省海洋与渔业科学院,海南 海口570125;2.中山大学 海洋学院,广东 广州 510275)
潮汐不对称与潮致余流在河口海岸区的物质输运中扮演着重要角色。已往的研究表明,在驻波占主导的河口海湾中,涨落潮的历时不对称与流速不对称有较为良好的对应关系。而潮致余流主要由地形与潮波的非线性作用所致。本研究以海南岛莺歌海附近为代表,结合实际观测与数值模型,研究复杂地形的开阔近岸区的潮汐不对称与潮致余流。结果表明,在莺歌海近岸区,涨落潮历时不对称皆表现为涨潮历时短于落潮历时,而流速不对称则出现复杂的空间变化。对流速不对称的机制分解表明,研究区的流速不对称主要由K1、O1与M2的相互作用,以及潮余流与各潮汐分潮的相互作用所控制。其中前者产生涨潮流速大于落潮流速的涨潮优势,而后者则与余流的方向相对应,出现多个涨潮优势与落潮优势的区域。总体而言,研究区的流速不对称由余流与各潮汐分潮的相互作用所决定。这表明,采用涨落潮历时的不对称来确定潮汐不对称的方法在开阔近海区可能并不适用。对潮致余流的研究表明,研究区的欧拉余流远大于斯托克斯余流。欧拉余流表现为多个顺时针与逆时针的涡流。涡流分布与地形具有较好的对应关系,潮流沙脊区多发育顺时针涡流,而深槽区则以发育逆时针涡流为主。摩擦力在涡流的发育中起着重要作用。
潮汐不对称;潮致余流;开阔近岸;海南岛
1 引言
潮汐与潮流是河口海岸中非常重要的动力因素。潮汐不对称是指在一个潮周期内涨落潮的历时与流速大小的不对称。如果涨潮历时短,涨潮流速大,则为典型的涨潮优势,反之则为落潮优势。在河口海岸地区,由于径流、风、地形等的复杂相互作用,还会出现涨潮历时长、涨潮流速也大的涨潮优势型,及落潮历时长与落潮流速大的落潮优势型[1]。潮汐不对称在河口海岸的环流、物质输运(如泥沙)等方面起着重要作用[2—3]。涨潮优势的河口基本以泥沙的净输入为主,而落潮优势的河口则更倾向于将泥沙向外海搬运。对于半日潮为主的海岸(如欧洲、北美东岸等)、日潮为主的海岸(如澳大利亚)及混合潮海岸,关于潮汐不对称的现象与机理已有大量的研究[4—8]。
潮致余流是不同分潮之间、以及潮汐与地形相互作用造成的一个潮周期平均后的流。潮致余流对悬浮物的净输运起着决定性作用。对于其描述,又分为欧拉余流与拉格朗日余流。欧拉余流指的是对一个固定点的潮流流速进行潮周期平均得到的剩余流动,而拉格朗日余流则是跟踪水质点的运动,采用潮周期内的位移除以时间得到的余流。欧拉余流的获取较为简易,而拉格朗日余流更能表达物质输运的概念。这里我们采用相对简单的方法计算这两种余流[9]。
总体而言,潮致余流控制着物质输运中的平流项(advective),而潮汐不对称则决定着物质输运中的潮泵项(tidal pumping),而上述项经常是物质输运中的主要成分,因而潮汐不对称与潮致余流的研究在物质输运、水质、生态系统的健康等方面都具有重要意义。
莺歌海位于海南岛西部,北部湾的东南部,潮汐作用较强,大潮潮差在2.5 m左右。潮汐中全日分潮K1、O1的振幅较大,而半日分潮(M2与S2)的振幅相对较小,其潮性系数F=HO1+HK1HM2+HS2=2.33,表明其为不正规日潮。对于不正规日潮的海区,其潮汐不对称的形成因素相对较为复杂,既有全日潮与半日潮之间的相互作用[8],也有主潮波与浅水潮波之间的相互作用的因素,如M2与M4之间,M2、S2与MS4之间,M2、K1与MK3之间等[7,10—11]。
受到强潮与波浪的共同作用,莺歌海的近岸地形表现出相当的复杂性。其近岸区在30 m等深线以内发育多条水下潮流沙脊,造成海底地形的剧烈起伏。而靠近岸线附近,由于波浪作用,近年来海滩的上部侵蚀较为剧烈,而侵蚀泥沙向岸外输运,在海滩的下部堆积,形成近岸较大面积水深小于2 m的浅水区[12]。这些复杂的动力与地形条件为研究开阔近岸的潮汐不对称与潮致余流提供了天然的实验场所。同时,本研究也将适合于类似的强潮海岸中流速不对称与余流的分析。
2 研究方法
为研究莺歌海附近的水动力状况,海南省海洋开发规划设计研究院于2012年12月12-13日大潮期在研究区布设6个定点连续观测站(图1,其中站位3因超出本研究区范围而未在图中标示),进行周日的潮流观测。测流采用日本ALEC公司的AEM-USB海流计,其测量精度流速在1.0 cm/s,流向在±2°。
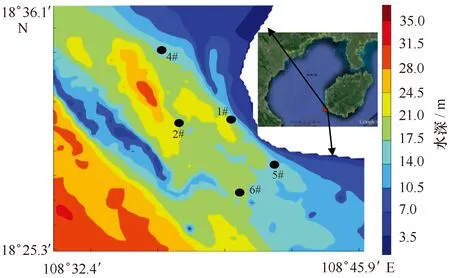
图1 研究区地理位置、实测站位与地形Fig.1 The geographic location, in-situ observation stations and bathymetry of the study site
由于现场测量的空间与时间覆盖有限,本研究采用数值模拟方法,获取更长时间与更大范围的流场数据。采用的数值模型为国际上广泛使用的Delft3D模型中的flow模块[13]。模型的研究范围如图1,网格尺寸为152×121,空间分辨为150 m左右。开边界采用潮汐调和常数以确定水位,分潮包括K1、O1、P1、Q1、M2、S2、N2、K2,这些分潮的调和常数来自于OPTS数据库。模型计算自2012年12月1日0:00开始,共计算31 d,其中前2天的数据作为模型起动(spin-up)时间,后29天的逐时数据用于以下的分析中。
在获取研究区的逐时水位与流速数据后,采用文献[6]的偏度方法来描述及水位与流速的不对称。其计算公式如下:
γ=μ3μ3/22,
(1)
μm=1N-1∑Ni=1(xi)m,
(2)
当x为流速时,γ表示流速不对称;当x为水位的时间导数时,γ表示为涨落潮历时的不对称。γ>0表示涨潮历时短于落潮历时。
此外,采用Tee[9]的方法计算潮致余流。
UE=〈u〉,
(3)
US=〈ζu〉h,
(4)
UL=UE+US,
(5)
式中,u为流速;ζ为瞬时水位;h为水深;UE为欧拉余流;US为斯托克斯余流;UL为拉格朗日余流。
3 模型验证
将模型计算值与实测的流速、流向资料进行对比。结果如图2所示。
计算结果显示,模型较好地复演了实测的流速变化,流速的最大均方根误差为3 cm/s,流向的最大均方根误差为11°,表明模型结果可用于研究区潮流场的进一步分析。
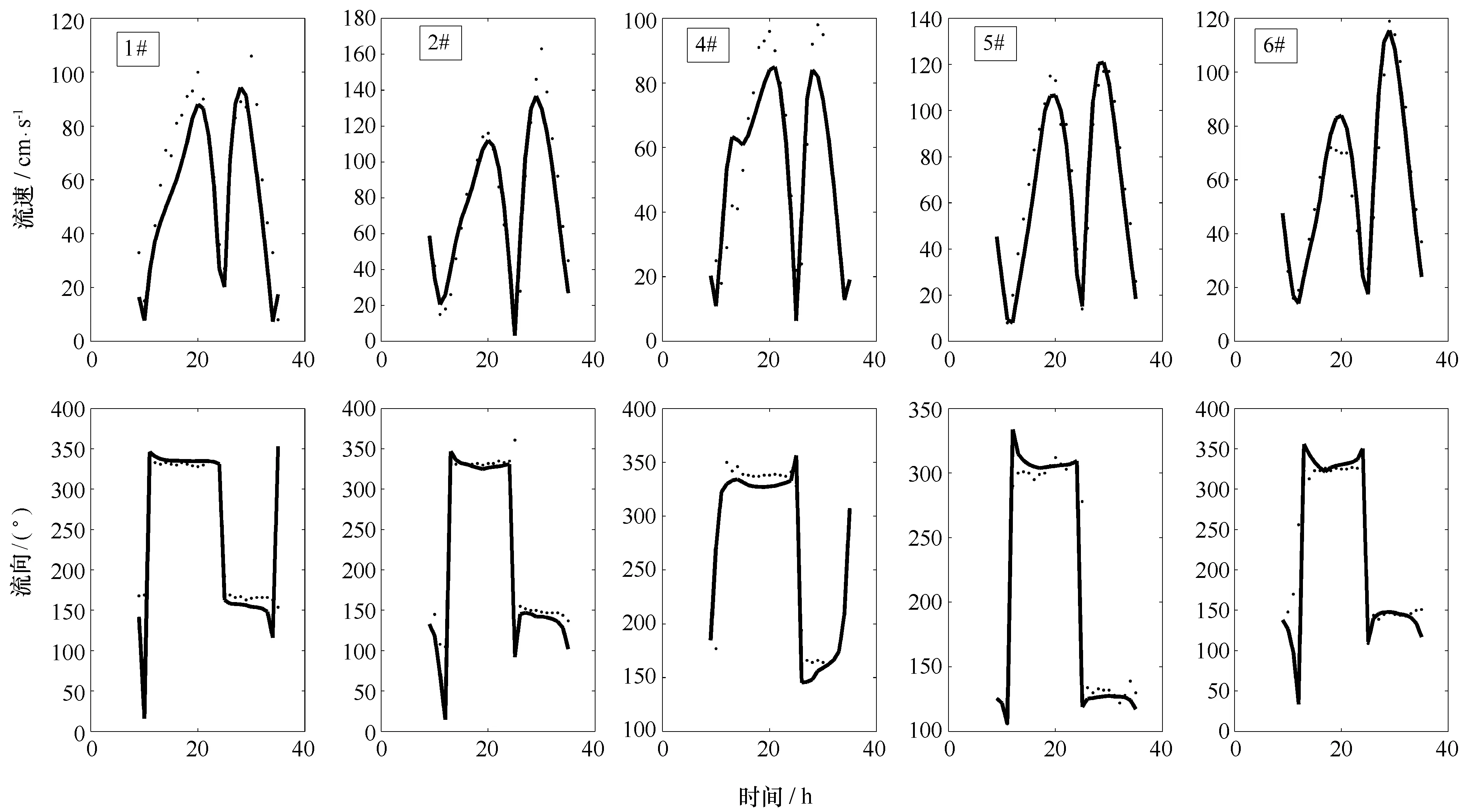
图2 模型验证(其中实线为模拟值,点划线为实测值)
Fig.2 Model calibration (solid line depicts model results, while dotted line shows the observations)
4 模型结果分析
4.1 流速不对称
对模型输出的29 d逐时水位与流速进行分析。对于水位,我们先求出水位变化的加速度,采用式(1)求出涨落潮历时的不对称。对于流速,先将研究区内各点的主流向求出[14],将逐时流速投影到主流向上,对主流向的流速采用式(1)求解其流速不对称状况。
计算得出的涨落潮历时与流速不对称的结果如图3所示。

图3 研究区涨落潮历时(a)与流速不对称(b)Fig.3 The flood-ebb duration asymmetry (a) and the velocity asymmetry (b)
研究区的涨落潮历时不对称系数γ>0,表现为涨潮历时短于落潮历时,这种情况在西北角处尤其突出。而流速不对称系数γ则发生较为复杂的变化,这里γ>0表示涨潮流速大于落潮流速的涨潮优势型,反之为落潮优势型。可以看出,研究区的西部以落潮优势为主,而研究区的东半部以涨潮优势为主,但局部也存在多个落潮优势型的分布区。
一般认为,在河口海岸区,不考虑径流与风的影响下,对于潟湖或海湾的口门,由于要满足一个潮周期内潮落潮流量基本相等的要求,涨潮历时短对应着涨潮流速大(涨潮优势),涨潮历时长对应着涨潮流速小(落潮优势)。Nidzieko和Ralston[15],Gong等[11]研究表明,这种情况只在潮波为驻波的潮汐汊道和海湾中才成立。本研究区为开阔近海,其潮波系统表现为以驻波为主,兼有前进波的性质[12],故涨落潮历时的不对称与流速大小的不对称并不对应。下面我们将更进一步分析流速不对称的控制因素。
4.2 潮致余流
我们对29 d的逐时流速数据进行调和分析,得出其欧拉余流如图4。研究区的欧拉余流量值最大可达0.3 m/s,但多数区域小于0.1 m/s。其空间分布呈现出较为复杂的格局,发育有多个涡流。下面我们将进一步分析欧拉余流的特征与形成机制。

图5 斯托克斯余流Fig.5 The Stokes residual current
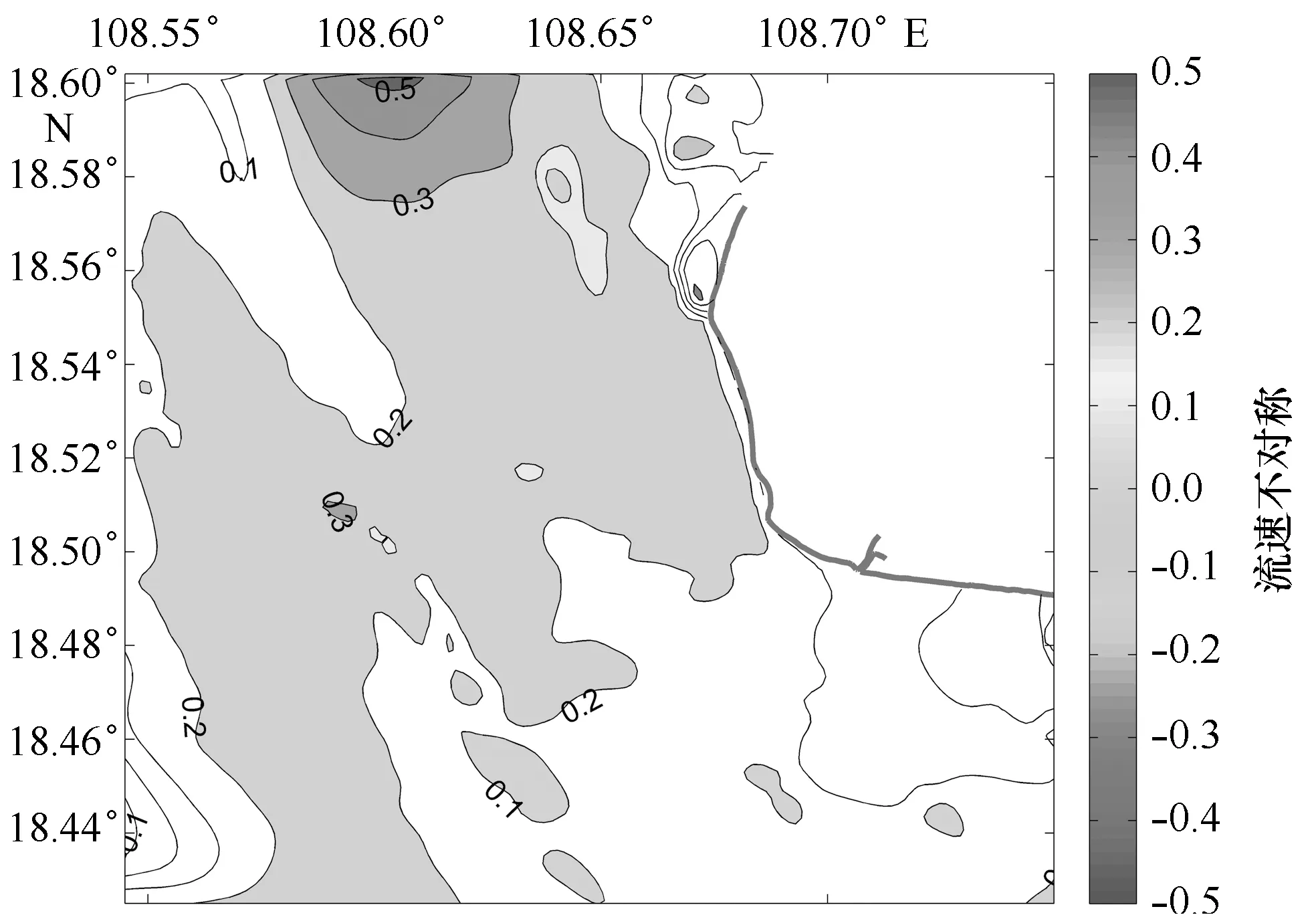
图6 K1、O1与M2相互作用形成的流速不对称Fig.6 The contribution of the interactions among K1,O1,and M2 to the velocity asymmetry

图7 余流项形成的流速不对称Fig.7 The contribution of the interactions among residual cur-rent and other tidal constituents to the velocity asymmetry

图8 潮流作用下的平均涡度(a为地形图,b为涡度)Fig.8 The mean tide-induced vorticity (a shows the bathymetry, b presents the vorticity)
此外,我们也计算了斯托克斯余流,其结果如图5。斯托克斯余流的量值很小,在0.01 m/s以下。这主要是因为研究区的潮波虽然兼有前进波的性质,但更接近驻波,实时水位与流速的相位差比较接近于90°[12],水位与流速相乘后潮周期的平均值很小。
因此,本研究区的拉格朗日余流主要由欧拉余流决定,其分布格局与欧拉余流类似(未用图显示)。
5 讨论
5.1 流速不对称的机理分析
对于不正规日潮的混合潮海区,控制流速不对称的因子可进一步分解为以下分量[10—11]:由K1、O1与M2的相互作用造成的γ0,由M2、S2与MS4的相互作用造成的γ1,由M2与M4的相互作用造成的γ2以及由余流与其他各分潮的相互作用造成的γ3。另外,K1、M2与KM3,O1、M2与MO3的相互作用也对潮汐不对称有一定贡献[10]。为此,我们对研究区各点的主流向流速进行潮汐调和分析,得出上述分潮的振幅与相位,求出相应的流速不对称分量。
从图6和图7计算结果来看,形成流速不对称的主要贡献项为K1、O1与M2的相互作用,以及由余流与其他各分潮的相互作用,其他各分潮的相互作用贡献很小(未用图表示)。总体而言,研究区的流速不对称由余流与各分潮的相互作用控制,其量值大小与分布格局决定了研究区的流速不对称。而K1、O1与M2的相互作用则总是产生正的流速不对称,即该项总是形成涨潮优势的不对称,这种格局与涨落潮历时的不对称相对应。由于总的流速不对称更多地由余流与各分潮的相互作用所决定,故总的流速不对称格局与余流的方向较为类似,如余流指向涨潮流方向,则流速不对称为正,反之则为负。结果表明,在径流量较小的潟湖、海湾等区域中大量存在的涨落潮历时不对称与涨落潮流速不对称的对应关系,在本研究区被彻底打破。从此延伸,采用水位观测数据来分析流速不对称的方法基本上不太可行,特别是近海开敞海岸。
5.2 潮致余流的形成机制
从欧拉余流与地形的对比来看,研究区水下沙脊与槽谷相间分布,形成多个余环流。总体来看,沿着沙脊基本发育顺时针的涡流,而沿着深槽则发育逆时针的涡流。这与世界上广泛存在的沿水下浅滩发育顺时针涡流的情况相一致[16]。
为进一步分析潮余流的形成机制,我们计算了平均涡度。从图8可以看出,地形与涡度有较好的相关,总体的格局为水深浅的区域以发育负涡度为主,水深较深的区域发育正涡度。另外,在岸线岬角附近,在岬角的上游侧(相对于开尔文潮波的传播方向)发育正涡(逆时针环流),在下游侧发育负涡(顺时针环流)。
对于涡度的正压输运方程为[17]:

(6)
式中,ω为相对涡度;Cd为摩擦系数;f为科氏力参数;t为时间;υ为水平黏性系数。项a表示水柱伸缩变化导致的涡度变化,项b表示流速剪切所造成的涡度变化,项c为水深梯度造成的涡度变化,项d为摩擦造成的涡度衰减,项e为由于水平混合造成的涡度变化。可见,涡度的变化主要由两部分控制:(1)根据位涡守恒定律,水深增大,其相对涡度增大,反之则减小;这可以很好地说明在水下沙脊发育顺时针环流,而在深槽处发育逆时针涡流的现象;(2)底摩擦作用导致的涡度变化。一般而言,水深浅的区域,摩擦力大,围绕其周围发育负涡度,而水深大的区域则易产生正涡度。Loder[18]的研究表明,顺着余流方向,其右手侧为水深浅的区域。这与本研究区的余环流分布相一致。
为进一步分析摩擦力对潮致余流的影响,我们设置了两个控制试验,分别将摩擦系数增大为原来的2倍和减小为原来的80%,计算其平均涡度(图9)。
结果表明,摩擦系数增大,平均涡度减少,余环流减弱;摩擦系数减小,平均涡度增大,余环流增强。说明摩擦力增大(减小)导致流速与其剪切减小(增大),从而使b项减小(增大),这一效应要大于流速减小(增大)从而使c和d项增大(减小)的效应。
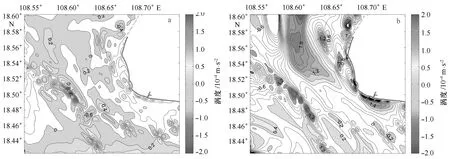
图9 摩擦力大小对平均涡度的影响(a为摩擦力增大的情况,b为摩擦力减小的情况)Fig.9 The impact of friction on the mean vorticity (a shows the situation with increased friction,b represents that with decreased friction)
6 结论
以海南岛莺歌海近岸为例,研究了开阔近海的潮汐不对称、潮致余流的特点及形成机制,对近岸的物质输运研究具有重要意义。主要结论如下:
(1)与潮波为驻波类型的潟湖、海湾不同,在近岸开阔水域根据水位序列计算的涨落潮历时不对称不能真实反映流速不对称的状况,而对物质输运起主要作用的是流速不对称。研究区的潮汐为不正规日潮,其流速不对称主要由两部分构成:K1、O1与M2的相互作用以及余流与各分潮的相互作用,其中后者占主导地位,决定了流速不对称的大小与空间分布。
(2)本研究区的潮致余流深受复杂地形的影响。潮流沙脊区以发育顺时针的涡流为主,而深槽区则主要发育逆时针涡流。在涡旋的发育中,水深变化所造成的水柱拉伸是造成涡流分布格局的一大因素,而非线性的摩擦项在涡旋的发育中起着重要作用。
[1] Jia Jianjun, Gao Shu, Xue Yunchuan. Sediment dynamic processes of the Yuehu Inlet system, Shandong Peninsula, China[J]. Estuarine, Coastal and Shelf Science, 2003, 57(5): 783-801.
[2] de Swart H E, Zimmerman J T F. Morphodynamics of tidal inlet systems[J]. Annual Review of Fluid Mechanics, 2009, 41: 203-229.
[3] Friedrichs C T. Tidal Flat Morphodynamics: A Synthesis[M]//Reference Module in Earth Systems and Environmental Sciences. Waltham: Elsevier, 2012.
[4] Aubrey D G, Speer P E. A study of non-linear tidal propagation in shallow inlet estuarine systems. Part 2: Observations[J]. Estuarine, Coastal and Shelf Science, 1985, 21(2): 185-205.
[5] Jewell S A, Walker D J, Fortunato A B. Tidal asymmetry in a coastal lagoon subject to a mixed tidal regime[J]. Geomorphology, 2012, 138: 171-180.
[6] Nidzieko N J. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides[J]. Journal of Geophysical Research, 2010,115, C08006, doi: 10.1029/2009JC005864.
[7] Song Dehai, Wang Xiaohua, Kiss A E, et al. The contribution to tidal asymmetry by different combinations of tidal constituents [J]. Journal of Geophysical Research, 2011,116: C12007.
[8] Hoitink A J F, Hoekstra P, van Maren D S. Flow asymmetry associated with astronomical tides: Implications for the residual transport of sediment[J]. Journal of Geophysical Research, 2003, 108(C10):3315.
[9] Tee K T. Tide-induced residual current, a 2-D nonlinear numerical tidal model[J]. Journal of Marine Research, 1976, 34(4): 603-628.
[10] 李谊纯. 一个潮流不对称计算方法及其在北仑河口的应用[J]. 海洋工程, 2014, 32(4): 110-116.
Li Yichun. A method of quantifying tidal current asymmetry and its application in the Beilun River estuary[J]. The Ocean Engineering, 2014, 32(4): 110-116.
[11] Gong Wenping, Schuttelaars H, Zhang Heng. Tidal asymmetry in a funnel shaped estuary with mixed semi-diurnal tides[J]. Ocean Dynamics, 2016, 66(5): 637-658.
[12] 龚文平, 张恒, 陈兆云, 等. 海南省乐东县莺歌海渔业加工区及配套码头建设项目岸滩演变分析[R]. 广州: 中山大学, 2016:129.
Gong Wenping, Zhang Heng, Chen Zhaoyun, et al. Analysis of coastal evolution of the Yinggehai fishery processing and companion dock project in Luodong, Hainan[R]. Guangzhou: Sun Yat-sen University, 2016:129.
[13] Lesser G R, Roelvink J A, van Kester J A T M, et al. Development and validation of a three-dimensional morphological model[J]. Coastal Engineering, 2004, 51(8/9): 883-915.
[14] Emery W J, Thomason R E. Data Analysis Methods in Physical Oceanography[M]. 2nd edition. Amsterdam: Elsevier, 2001.
[15] Nidzieko N J, Ralston D K. Tidal asymmetry and velocity skew over tidal flats and shallow channels within a macrotidal river delta[J]. Journal of Geophysical Research , 2012, 117:C03001.
[16] Yuan Jiliang, Yang Zhaoqing, Huang Daji, et al. Tidal residual current and its role in the mean flow on the Changjiang Bank[J]. Journal of Marine Systems, 2014, 154: 66-81.
[17] Robinson I S. Tidal vorticity and residual circulation[J]. Deep-Sea Research Part A. Oceanographic Research Papers, 1981, 28(3): 195-212.
[18] Loder J W. Topographic rectification of tidal currents on the sides of Georges Bank[J]. Journal of Physical Oceanography, 1980, 10(9): 1399-1416.
Tidal asymmetry and tide-induced residual currents in the Yinggehai Coast, Hainan Island
Lin Guoyao1, Gong Wenping2
(1.HainanProvincialMarineandFisheryResearchInstitute,Haikou570125,China; 2.SchoolofMarineScience,SunYat-senUniversity,Guangzhou510275,China)
Tidal asymmetry and tide-induced residual circulation play important roles in mass transport in estuarine and coastal seas. Previous studies have shown that the flood and ebb duration asymmetry corresponds well to the tidal velocity asymmetry in estuaries and embayments where standing tidal waves dominate. The tide-induced residual circulation is mainly from the nonlinear interaction between tides and bathymetry. This study takes the Yinggehai Coast as an example to study the tidal asymmetry and residual circulation in open coast with complex bathymetry, through combination of field observation and numerical simulation. Our results show that the flood duration is shorter than the ebb duration, while the velocity asymmetry manifests a complex spatial variability. The underlying mechanisms are that the velocity asymmetry is mainly induced by the interactions among K1, O1, and M2and the interactions among the residual flow and tidal constituents. The former contribution results in a flood dominance, while the latter contribution results in a spatial distribution similar to the residual current. Overall, the interactions among the residual current and tidal constituents determine the pattern of the velocity asymmetry. For the tide-induced residual current, the Euler residual is greatly stronger than the Stokes one. There exist many clockwise and anti-clockwise eddies in the study site, and the clockwise eddies are generally associated with the tidal sand ridges well, while the anti-clockwise eddies are located in the deep troughs. The conservation of potential vorticity largely determines the residual circulation pattern, along with the bottom friction playing a critical role as well.
tidal asymmetry; tide-induced residual circulation; open coast; Hainan Island
2016-07-07;
2016-10-29。
广东省重点基金(2014A030311046)。
林国尧(1963—),男,海南省海口市人,从事海洋工程研究。E-mail:linguoyao63@qq.com
*通信作者:龚文平。E-mail:gongwp@mail.sysu.edu.cn
10.3969/j.issn.0253-4193.2017.07.004
P731.23
A
0253-4193(2017)07-0036-07
林国尧, 龚文平. 海南岛莺歌海近岸的潮汐不对称与潮致余流研究[J]. 海洋学报, 2017, 39(7): 36-42,
Lin Guoyao, Gong Wenping. Tidal asymmetry and tide-induced residual currents in the Yinggehai Coast, Hainan Island[J]. Haiyang Xuebao, 2017, 39(7): 36-42, doi:10.3969/j.issn.0253-4193.2017.07.004

