一种新型电阻补偿双极工艺带隙基准电压源

吴 越, 尹勇生, 陈红梅

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)

一种新型电阻补偿双极工艺带隙基准电压源

吴 越, 尹勇生, 陈红梅

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)

文章分析了带隙基准电压源中电阻补偿的原理,使用2种不同温度系数的电阻设计了一个低温度系数新型双极工艺带隙电压源电路,并基于CSMC 2 μm36 V 双极工艺对电路进行仿真,实现了对基极发射极电压的三阶补偿。仿真结果表明,在10～30 V输入电压范围内,该带隙电压源输出电压为2.12 V;电源抑制比为120.2 dB的频率点为14.85 Hz;温度变化范围在-40～125 ℃时,温度系数为2.17×10-6/℃。

电阻补偿;带隙基准源;双极工艺;温度系数;线性调制率;电源抑制比

0 引 言

基准电压源是集成电路中的基本模块,它的功能就是产生一个与电源和工艺无关、几乎不受噪声影响且不随环境温度改变的直流电压并为电路提供稳定偏置,它被广泛应用于A/D、D/A、脉冲宽度调制(pulse-width modulation, PWM)控制器、传感器和充电管理芯片中,它产生的基准电压精度、温度稳定性、驱动负载能力直接影响到芯片,甚至整个系统的性能[1]。

按照对温度的补偿阶数来分类,基准电压源可分为零阶、一阶、二阶、高阶基准电压源。零阶基准电压源的基准电压一般由正向偏置的二极管或反偏的齐纳二极管产生,这类基准输出电压的温漂系数一般在±2 mV/℃左右,且都未对温度进行补偿,它们的面积小、结构简单便于集成,但存在噪声大、负载能力弱、稳定性差以及基准电压较高、可调性较差等缺点。目前应用最多的一阶基准电压源是一阶带隙基准电压源,它采用晶体管-晶体管逻辑电路(transistor-transistor logic, TTL)、互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)等技术实现,利用一个与温度成正比的电压与一个与温度成反比的电压之和,两者温度系数相互抵消,从而实现对温度的一阶补偿,基准输出电压约为1.25 V,因为其输出电压与硅的带隙电压差不多,所以称为带隙基准,这种基准电压源的温漂系数一般在(50～100)×10-6/℃,具有面积小、功耗低、工艺兼容性高、低噪声、高精度等诸多优点[2]。

随着市场对具有低输出动态范围和低电压摆幅特性的供电集成电路(integrated circuit,IC)需求不断增长,上述零阶和一阶基准电压源不再能够满足大量高性能系统的使用需求。例如,在高性能数据转换器、移动通信芯片和电池充电管理芯片等应用场合中,这类芯片输入电压动态范围大,且常会工作在高温高压恶劣环境下,上述基准源就不能保证产生精准、稳定的输出电压,因此,需要采用按照曲率校正技术对温度进行二阶或高阶补偿的曲率补偿带隙基准电压源[3]。

常见的高阶曲率补偿技术有二极管环路法[4]、分段线性补偿法[5]、非线性匹配补偿法[6]等,均能有效使温度系数降低到50×10-6/℃以下。二极管环路法是由具有不同温度系数的电流以及电阻、晶体管组成环路来实现,适用于在低电源电压下应用,温度系数在3×10-6/℃左右,但是静态电流较大且电流对温度较敏感。分段线性补偿法引入额外的补偿电压,对芯片工作的各个温度区间分别使用不同的补偿电压对温度进行补偿,结构较简单,但补偿后温度系数约在25×10-6/℃,补偿效果不显著。非线性匹配补偿法是通过产生一个具有对数温度特性的补偿电压实现温度补偿,温度系数通常在10×10-6/℃以下,但结构较复杂,成本较高。电阻补偿法是利用具有不同温度特性的电阻产生非线性电压分量实现温度补偿的方法,增加1～2个电阻即可以获得很低的温度系数,通常在5×10-6/℃以下,只需要对原电路做简单调整即可实现,结构简单、成本低廉,具有很强的实用性。

金属氧化物半导体(metal-oxide semiconduc-tor, MOS)工艺凭借其高集成度、低功耗的特点在现代模拟集成电路的设计中得到了大量应用[7],但双极(bipolar)工艺与MOS工艺相比具有高速、高跨导、强电流驱动能力、高精度、所需偏置电压较低的优点,尤其是在低频工作段内,双极工艺具有更低的噪声,并且能提供精确定义的正、负温度系数。在低电压设计中,CMOS器件需要大栅极宽度才能获得很大的漏电流,而双极型晶体管的基极电压仅需提高约60 mV/℃,即可实现集电极电流10倍的增长。因此在低频低压型电路设计中,特别是带隙基准电压源的设计中双极工艺比CMOS工艺更具优势,仍被优先应用[8]。

本文利用不同类型电阻的温度系数差异,设计了一种三阶补偿带隙基准源,基于双极工艺对电路进行仿真和实现,并已应用到一款电池充电管理芯片中。

1 电路原理及结构分析

1.1 带隙基准原理

文献[9]通过对双极型晶体管的深入研究,发现基极发射极的负温度系数电压Vbe可以与一个与热力学温度成正比(proportional to absolute temperature, PTAT)的电压相互抵消,该PTAT电压可以由2个Vbe的电压差得到,即

(1)

其中,IC为集电极电流;AE为发射极面积。

带隙基准原理如图1所示。

图1 带隙基准原理图

基准电压Vref的表达式为:

(2)

其中,m′为实际电路中电阻系数比。

其中，VG0为绝对零度时硅的带隙电压；VT为热电压。

所得到的具有零温度系数的输出电压的值略高于硅的带隙基准电压,室温下输出电压约为1.25 V,将这种电路称为带隙基准电压源。

1.2 高阶电阻补偿原理

三极管的基极发射极电压表达式[10]为:

(3)

其中,VG(Tr)为给定常数温度Tr下的带隙电压;η为电场因子,是工艺常数;IC为集电极电流。应用到电阻补偿法中时,可将(3)式泰勒展开[11]转化为：

(4)

通过仿真迭代求解,可获得较精确的各项系数值。

传统的一阶带隙基准源都是将具有正温度系数的线性PTAT电压与Vbe相加来抵消一阶系数b的影响,其波形特征为抛物线。而在此基础上,二阶带隙基准源采用曲率校正技术,引入具有非线性正温度系数的PTAT二阶电压来抵消二阶系数c的影响,产生带有2个极点的T3波形。以此类推,引入PTAT三阶电压后,合理调整电路,可以抵消三阶温度系数对Vbe的影响,得到Vref关于T4的温漂波形[12]。

不同类型电阻的温度系数通常具有差异性,可以利用其来产生非线性分量,电阻补偿原理如图2所示,基准电压可以表示为:

(5)

图2 电阻补偿原理图

(5)式中,R1和R2具有相同的温度系数,R3的温度系数大于R1,从而可以产生所需要的高阶PTAT分量。电阻温度表达式[13]为:

(6)

其中,ptc1、ptc2分别为电阻的一阶和二阶温度系数。

联立(2)～(4)式,可得到Vref的表达式为:

(7)

(8)

(9)

则可确定R2(T0)和R3(T0)的值。

1.3 电路结构分析

利用上述方法,本文采用CSMC 2 μm36 V双极工艺设计了带隙基准电路,如图3所示,其中Q5、Q15～Q17、R4、R5组成启动电路,Q12～Q14为偏置电路,Q1～Q4、Q6～Q9、C1为三级运放电路、Q10、Q11、R2、R3组成带隙基准核心电路。

图3 电路结构图

当电源上电时,启动支路导通,Q5为运放供电,从而使整个电路导通,当电路开始工作后,Q5关断。带隙核心电路不仅输出Vref电压,并通过Q10～Q14组成的电流镜为运放电路提供偏置,运算放大器起到了稳定输出电压的作用,Q7～Q9组成复合放大管,当输出电压升高时,运放输入级Q1、Q2电压差增大,使得Q6的基极电压降低,流入电阻网络的电流减小,从而使输出电压下降;当输出电压下降时,运放输入级Q1、Q2的电压差降低,使得Q6的基极电压升高,其流入电阻网络的电流增大,使输出基准电压回升。

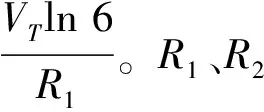
2 仿真结果和版图实现

利用Cadence Spectre对电路进行前仿,仿真结果如图4～图6所示。

图4 温度系数前仿图

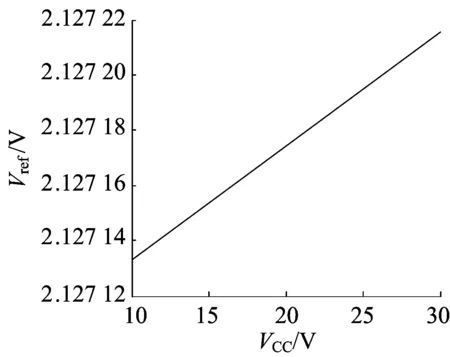
图5 线性调整率前仿图

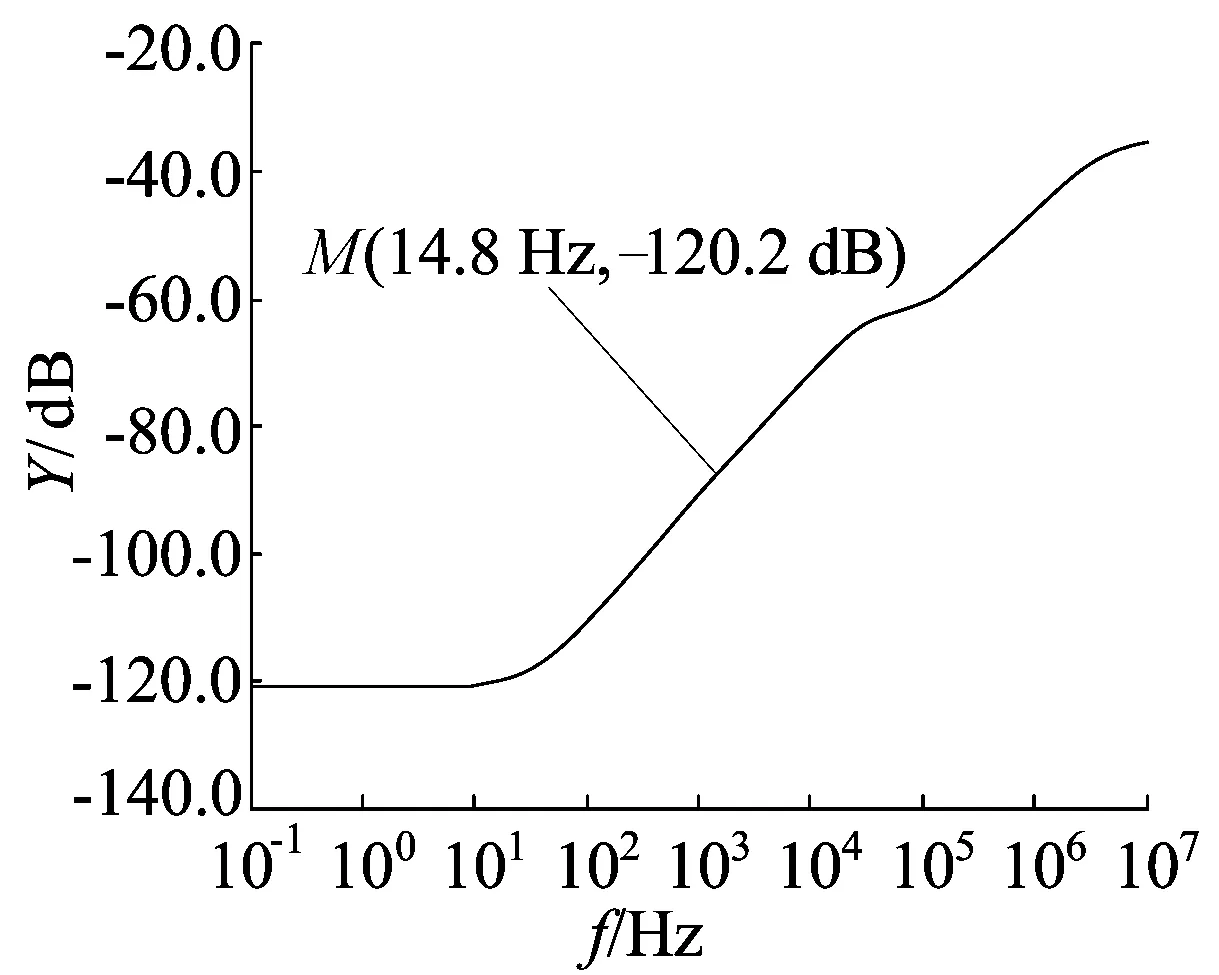
图6 电源抑制比前仿图

温度系数是衡量带隙基准电压源输出电压随温度变化的一个重要指标。温度系数越小,输出信号受温度的影响就越小。其计算公式为:

(10)

其中,Vmean为仿真温度范围内输出电压平均值。

结合(10)式和图4仿真结果可得,该带隙基准电路在-40～125 ℃温度范围内,温度系数为0.66×10-6/℃。其输出波形也不再是一阶带隙基准的“彩虹线”,而是带有3个极点的曲线。

基准电压源的线性调整率表示在规定电源电压范围内,单位电源电压的变化引起基准电压变化的百分数,线性调整率越小,说明电源电压对基准电压源的输出电压影响越小。图5仿真结果表明,当输入电压在10～30 V范围内,该带隙基准电压源输出电压稳定在2.12 V左右,线性调整率为0.004 mV/V。

电源抑制比是衡量电路对电源线上噪声抑制能力的重要参数。对于带隙基准电路而言,高的电源抑制比尤为重要。因为带隙基准电压源电路的输出若与误差放大器等模块相连,作为误差放大器差分输入的一部分,则当电源噪声没有得到抑制时,将会作为误差放大器的输入信号的一部分被放大从而影响电路的输出信号,所以在设计带隙基准电压源电路时,要尽可能地提高电路的电源抑制比。图6仿真结果表明,电源抑制比为-120.2 dB时的频率点为14.85 Hz,满足应用需求。

根据上述设计绘制的电路版如图7所示。由于该电路采用电阻补偿技术,要求电阻具有较高精确度,并要注意电阻的匹配性,因此该版图采用宽尺寸电阻条并尽量保持其方块数不变,将需要匹配的电阻沿同一方向摆放,使其尽可能靠近。

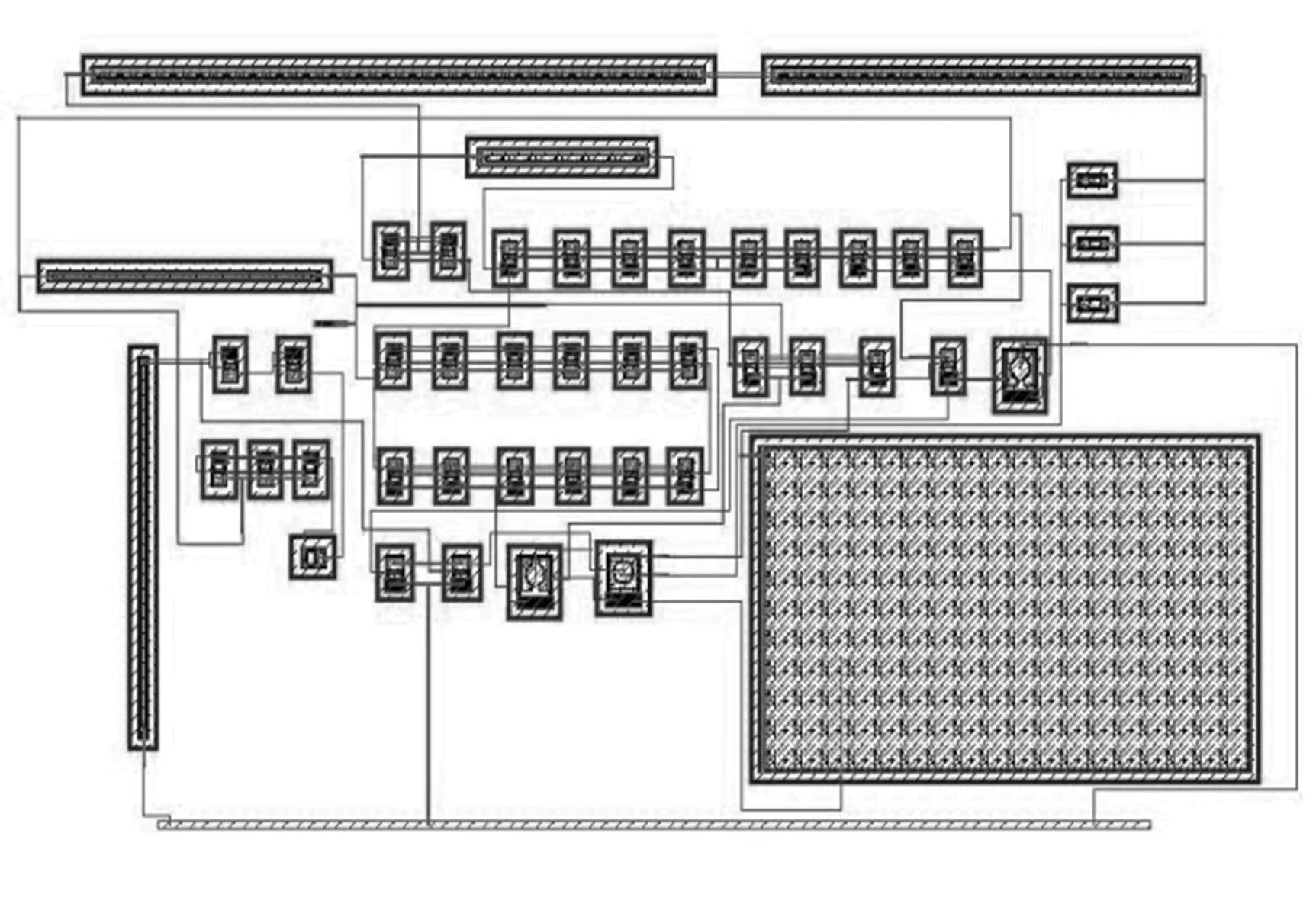
图7 电路版图

使用Cadence Dracula对电路版图进行验证,并提取寄生参数,将带有寄生参数的Hspice格式网表导入Hspice中,并重点对温度系数进行了后仿,得到仿真结果如图8所示。后仿输出电压曲线与前仿趋势基本相同,后仿温度系数为2.17×10-6/℃,与前仿差别不大,这表明上述电阻补偿理论和结构设计正确可靠。

与文献[13-15]比较,文献[13-14]均采用二阶补偿设计,温度系数分别为7×10-6/℃和4.5×10-6/℃,本文设计实现了更高阶补偿且温度系数指标优于上述文献,并通过了后仿验证;文献[15]的温度系数为2.2×10-6/℃,与本文所设计的带隙基准温度指标接近,但电路结构复杂程度高于本设计。

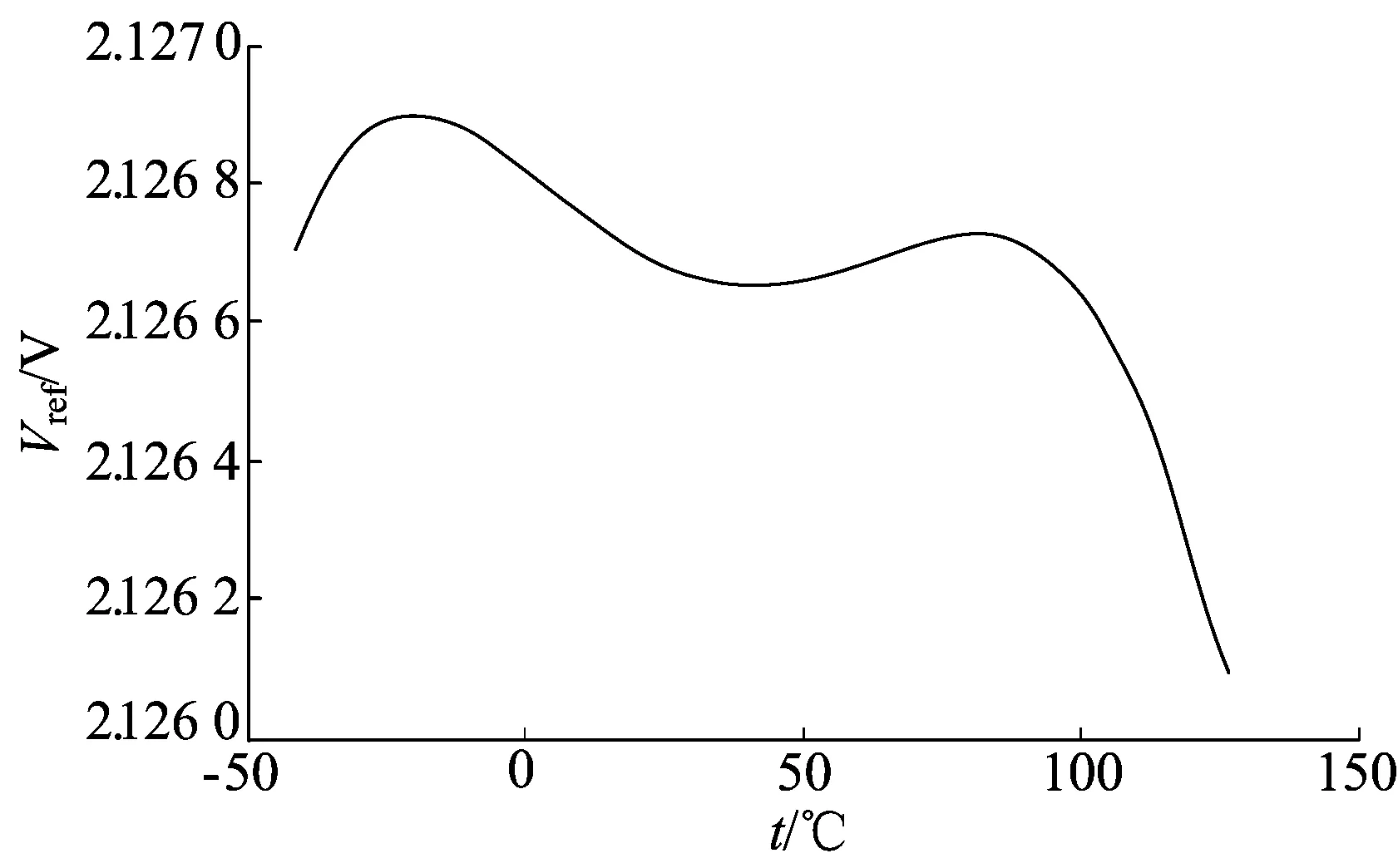
图8 温度系数后仿图

3 结 论

本文分析了带隙基准电路中电阻补偿原理,并将其运用到具体电路中。这种方法的核心是引入非线性变量,先通过泰勒展开简化相应公式,然后求导得到相应估算阻值,再通过迭代仿真最终得到理想的波形,具有较强的实用性和操作性,同时也可以扩展到其他工艺中应用。

[1] 何乐年,王忆.模拟集成电路设计与仿真[M].北京:科学出版社,2008:196-232.

[2] RAZAVI B.模拟CMOS集成电路设计[M].陈贵灿,程军,张瑞智,等,译.西安:西安交通大学出版社,2002：307-327.

[3] LEWIS S R,BROKAW A P.Curvature correction of bipolar bandgap references:US4808908[P].1989-02-28.

[4] GUNMAN M. A curvature corrected low voltage bandgap refernces[J].IEEE Journal of Solid-State Circuits,1993,28(6):667-670.

[5] 姜树法,张国俊.分段温度曲率补偿双极工艺带隙基准设计[J].微电子学与计算机,2013,30(4):75-78.

[6] 唐宁,李佐,李琦.一种改进的非线性匹配高阶补偿基准源的设计[J].电子器件,2013,36(6):797-800.

[7] 瞿美霞,尹勇生,邓红辉.一种适用于数模转换电路的带隙基准电压源[J].合肥工业大学学报(自然科学版),2008,31(7):1128-1130,1144.

[8] GRAY P R.模拟集成电路的分析与设计[M].张晓林,译.北京:高等教育出版社,2005:301-319.

[9] WILDAR R J.New developments in IC voltage regulators[J].IEEE Journal of Solid-State Circuits,1971,6(1):2-7.

[10] TSIVIDIS Y P.Accurate analyzes of temperature effects inIcandVbe[J].IEEE Journal of Solid-State Circuits,1980,15(6):1076-1084.

[11] AUDY J M.Bandgap voltage reference circuit and method with low TCR resistor in parallel with high TCR and in series with low TCR portions of tail resistor:US5291122[P]. 1994-05-01.

[12] AUDY J M.3rd order curvature corrected bandgap cell[C]//Proceedings of the 38th Midwest Symposium on Circuits and Systems, Vol 1.[S.l.:s.n.],1995:397-400.

[13] 胡波,李骏,廖良,等.一种实用的曲率补偿带隙基准电压源[J].微电子学,2007,37(5):764-767.

[14] 徐静平,熊剑波,陈卫兵.一种新的CMOS带隙基准电压源设计[J].华中科技大学学报(自然科学版),2006,34(2):36-38.

[15] 苑婷,巩文超,何乐年.高精度、低温度系数带隙基准电压源的设计与实现[J].电子与信息学报,2009,31(5):1260-1263.

(责任编辑 张淑艳)

A Bipolar bandgap voltage reference with resistance compensation

WU Yue, YIN Yongsheng, CHEN Hongmei

(School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei 230009, China)

In this paper, the principle of the resistance compensation in the bandgap voltage reference is analyzed. A new type of Bipolar bandgap voltage source circuit with low temperature coefficient is designed by using two different temperature coefficient resistors, the circuit is simulated and realized based on CSMC 2 μm36 V Bipolar process, and the three-order base-emitter voltage compensation is realized. The simulation results show that the output voltage is 2.12 V in the range of 10-30 V input voltage. The power supply rejection ratio(PSRR) is 120.2 dB when the frequency is 14.85 Hz. When the temperature ranges from -40 ℃ to 125 ℃, the temperature coefficient is 2.17×10-6/℃.

resistance compensation; bandgap voltage reference; Bipolar process; temperature coefficient; line regulation; power supply rejection ratio(PSRR)

2015-12-10；

2016-02-29

中央高校基本科研业务费专项资金资助项目(2014HGCH0010)

吴 越(1988-)，男,安徽巢湖人,合肥工业大学硕士生; 尹勇生(1973-)，男,内蒙古锡林浩特人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.05.028

TN431.1

A

1003-5060(2017)05-0716-05