基于MQ拟插值的Burgers-Fisher方程数值解法

高钦姣, 张胜刚, 何素艳, 曹宏举

(1.大连外国语大学 经济与管理学院,辽宁 大连 116044; 2.大连医科大学 公共卫生学院,辽宁 大连 116044; 3.大连外国语大学 软件学院,辽宁 大连 116044)

基于MQ拟插值的Burgers-Fisher方程数值解法

高钦姣1, 张胜刚2, 何素艳3, 曹宏举3

(1.大连外国语大学 经济与管理学院,辽宁 大连 116044; 2.大连医科大学 公共卫生学院,辽宁 大连 116044; 3.大连外国语大学 软件学院,辽宁 大连 116044)

文章利用 MQ 拟插值构造了求解Burgers-Fisher 方程的无网格数值方法。在时间方向,用向前差分法对方程进行离散; 在空间方向,用 MQ 拟插值及其导数逼近函数本身及其空间导数。该方法的特点是操作简单,不用求解大型的方程组,稳定性好。最后,将该方法与精确解的误差和其他方法与精确解的误差进行了比较,结果显示MQ拟插值方法求解此类方程表现更好。

MQ函数;Burgers-Fisher 方程;拟插值

0 引 言

Burgers-Fisher方程在气体动力学、热传导和弹性力学中都有重要的应用,是国内外研究的热点问题[1]。研究Burgers-Fisher方程的数值解问题既对流体力学的研究具有重要意义,也可以检测数值方法的有效性。

自20世纪60年代以来,关于上述方程解析解和数值解的研究成果丰富。在解析解方面,文献[2]研究了应用 Adomian 分解法的 Burgers-Huxley 和 Burgers-Fisher 方程;文献[3]给出了广义形式的非线性热传导和 Burgers-Fisher 方程的 tanh 方法;文献[4] 研究谱域分解法求解广义 Burgers-Fisher 方程的方法。在数值解方面,文献[5] 给出了一个非标准的 Burgers-Fisher方程的有限差分格式;文献[6]介绍了数值模拟和广义 Burgers-Fisher 方程的精确解;文献 [7] 提出解决广义 Burgers-Fisher方程的限制性Padé 逼近;文献[8-9] 分别给出Burgers-Fisher 方程的有限差分数值解法。基于网格的有限元、有限差分等方法在微分方程数值解中应用广泛[10-13],但它们在处理大曲率、大变形、激波等问题时,会产生计算量大、格式不稳定的问题。

为了克服传统数值方法对网格的依赖性,近年来,越来越多的专家学者利用无网格方法求微分方程的数值解。无网格方法[12-13]将函数的构造建立在一系列离散的节点上,这类方法对求解区域以及网格的设置没有任何限制,并且无网格方法具有计算简便、高效、易于操作的特点,受到数学和工程界的欢迎。

文献[14-16]分别利用一类无网格法MQ拟插值法求解Burgers方程,数值试验结果效果良好、操作简便。文献[17-18]从理论上证明了MQ拟插值的高阶导数的逼近阶和稳定性,从而为MQ拟插值求解微分方程奠定了理论基础。考虑到在拟合Burgers-Fisher方程时与Burgers方程数值解的相似性,文献[12]提出使用B样条拟插值方法求Burgers-Fisher方程的数值解,并取得了满意的效果。

与B样条拟插值方法相比,MQ拟插值具有精度高、稳定性好、表达式更加简单,从而更易于操作等优点。基于以上考虑,本文运用一类MQ拟插值求Burgers-Fisher方程的数值解。首先将方程在时间方向用有限差分方法进行离散,然后在空间方向使用MQ拟插值逼近函数本身和函数的各阶导数,给出基于MQ拟插值的数值方法。

1 数值方法

Burgers-Fisher方程[19]为:

(1)

该方程初始条件为:

(2)

边界条件为:

(3)

及

(4)

在上述条件下,方程的精确解为:

(5)

其中α、β、δ为系数。

当α=1,β=0,δ=1时,Burgers-Fisher方程变为带黏性的Burgers方程。考虑到这一点,文献[14-16]用MQ拟插值很好地拟合了Burgers方程,本文考虑用其来拟合Burgers-Fisher方程。在拟合Burgers方程时,用简单的有限差分法并不能得到满意的结果,MQ拟插值法在拟合Burgers-Fisher方程时比有限差分法、有限元法等方法更有优势。

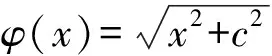
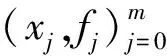
定理1[16]在区间[x0,xm]上,拟插值f*(x)可以写成:

且在[x0,xm]上有:

在此基础上,对带有初始条件(2)和边值条件(3)、(4)的广义Burgers-Fisher方程(1),本文给出基于MQ拟插值的方法如下:

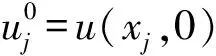
(2) 将带有上述初始条件和边值条件的Burgers-Fisher方程在时间方向离散为:

与其他方法相比,上述算法编程简单、稳定性好,并且不需要求解大规模的矩阵的逆,下一节的数值试验说明该算法的可行性。

2 数值实验

本节用MQ拟插值方法(MQQI)求在初值条件(2)和边值条件(3)、(4)的Burgers-Fisher方程(1)的数值解。

选择与B样条拟插值方法(B-Spline quasi-interpolation,BSQI)[12]进行比较,这是因为与SCM(spectral collocation method)方法、SDD(spectral domain decomposition)方法等相比,就精确度和简便性而言,B样条拟插值方法都表现更好。下面给出数值例子,验证本文方法的可行性。设h=1/15,τ=0.000 1，根据形状参数的理论[18]以及多次实验结果知:

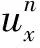
例1 本文使用上述方法求当α=0.001,β=0.001时的Burgers-Fisher方程(1)的数值解。对不同的δ、t,MQ拟插值法在不同时间的最大模误差,并与B样条拟插值方法进行了比较，见表1所列。数值结果表明MQ拟插值法的表现更好。

例2 本文使用上述方法求当α=0.1,β=-0.002 5时的Burgers-Fisher方程(1)的数值解。对不同的δ、t,MQ拟插值法在不同时间的最大模误差,并与B样条拟插值方法进行了比较，见表2所列。数值结果表明MQ拟插值法的表现更好。

表1 当α=0.001,β=0.001时,不同δ、t的最大模误差

表2 当α=0.1,β=-0.002 5时,不同δ、t的最大模误差

3 结 论

本文使用MQ拟插值数值求一类带有初边界条件的Burgers-Fisher方程的数值解,给出了数值方法:首先将方程在时间方向进行离散,然后用MQ拟插值逼近固定时间层上的离散点。将此算法应用于实际例子,并与B样条拟插值方法进行了比较,结果表明本文方法的表达式比B样条拟插值方法的表达式简单,并且本文方法的误差可以满足工程界对求解精度的需求。实验证明MQ拟插值法精度高,稳定性好,易于操作。

[2] WAZWAZ A M,GORGUIS A.An analytic study of Fishers equation by using Adomian decomposition method[J].Applied Mathematics and Computation,2004,154(3):609-620.

[3] WAZWAZ A M.The tanh method for generalized forms of nonlinear heat conduction and Burgers-Fisher equations.Applied Mathematics and Computation[J].2005,169(1):321-338.

[4] GOLBABAI A,JAVIDI M.A spectral domain decomposition approach for the generalized Burgers-Fisher equation[J].Chaos,Solitons & Fractals,2009,39(1):385-392.

[5] MICKENS R E,GUMEL A B.Construction and analysis of non-standard finite difference scheme for the Burgers-Fisher equation[J].Journal of sound and vibration,2002,257(4):791-797.

[6] KAYA D,EI-SAYED S M.A numerical simulation and explicit solutions of the generalized Burger-Fisher equation[J].Applied Mathematics and Computation,2004,152(2):403-413.

[7] ISMAIL H N A,RABBOH A A A.A restrictive Padé approximation for the solution of the generalized Fisher and Burger-Fisher equation[J].Applied Mathematics and Computation,2004,154(1):203-210.

[8] BABOLIAN E,SAEIDIAN J.Analytic approximate solutions to Burgers,Fisher,Huxley equations and two combined forms of these equations[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(5):1984-1992.

[9] 陈晓永.Burgers-Fisher方程的数值解法[D].南京:南京航空航天大学,2007.

[10] 郭清伟,张官升.具有给定测地线的三次三角Bézier曲面的构造与拼接[J].合肥工业大学学报(自然科学版),2014,37(1):125-128.

[11] 朱晓临,陈嫚,李雪艳,等.结合形态学变形虫和复合颜色空间的彩色图像边缘检测模型[J].计算机辅助设计与图形学学报,2014,26(7):1060-1066.

[12] ZHU C G,KANG W S.Numerical solution of Burgers-Fisher equation by cubic B-spline quasi-interpolation[J].Applied Mathematics and Computation,2010,216(9):2679-2686.

[13] MITTAL R C,TRIPATHI A.Numerical solutions of generalized Burgers-Fisher and generalized Burgers-Huxley equations using collocation of cubic B-splines[J].International Journal of Computer Mathematics,2015,92(5):1053-1077.

[14] HON Y C,MAO X Z.An efficient numerical scheme for Burgers’ equation[J].Applied Mathematics and Computation,1998,95(1):37-50.

[15] GAO W W,WU Z M.Solving time-dependent differential equations by multi-quadric trigonometric quasi-interpolation[J].Applied Mathematics and Computation,2015,253:377-386.

[16] CHEN R H,WU Z M.Applying multi-quadratic quasi-interpolation to solve Burgers’ equation[J].Applied Mathematics and Computation,2006,172:472-484.

[17] MA L M,WU Z M.Approximation to the k-th derivatives by multi-quadric quasi-interpolation method[J].Journal of Computational and Applied Mathematics,2009,231(2):925-932.

[18] MA L M,WU Z M.Stability of multi-quadric quasi-interpolation to approximate high order derivatives[J].Science China Mathematics,2010,53(4):985-992.

[19] ISMAIL H N A,RASLAN K,RABBOH A A A.Adomian decomposition method for Burgers’ Huxley and Burgers-Fisher equations[J].Applied Mathematics and Computation,2004,159(1):291-301.

(责任编辑 朱晓临)

Numerical solution of Burgers-Fisher equation based on MQ quasi-interpolation

GAO Qinjiao1, ZHANG Shenggang2, HE Suyan3, CAO Hongju3

(1.School of Economics and Management, Dalian University of Foreign Languages, Dalian 116044, China; 2.School of Public Health, Dalian Medical University, Dalian 116044, China; 3.School of Software, Dalian University of Foreign Languages, Dalian 116044, China)

In this paper, the meshless numerical method for Burgers-Fisher equation based on the multi-quadric(MQ) quasi-interpolation is presented. In the temporal direction, a low order forward difference is applied to approximating the time derivative of the dependent variable. In the spatial direction, the derivative of the MQ quasi-interpolation is applied to approximating the spatial derivative of the dependent variable. The algorithm is very simple, stable and does not need to solve the large-scale equations. The error between the numerical result of this method and the exact solution is compared with that between the result of other method and the exact solution to show the better performance of the presented method.

multi-quadric(MQ) function; Burgers-Fisher equation; quasi-interpolation

2016-03-20；

2016-08-31

国家自然科学基金青年科学基金资助项目(11501006);辽宁省教育厅自然科学一般资助项目(L2013434);辽宁省教育科学“十二五”规划资助项目(JG12DB318)和大连外国语大学校级青年资助项目(2014XJQN11)

高钦姣(1986-),女,山东日照人,博士,大连外国语大学讲师; 张胜刚(1983-)，男，湖北黄冈人，大连外国语大学讲师； 何素艳(1963-),女,河北保定人,博士,大连外国语大学教授.

10.3969/j.issn.1003-5060.2017.05.027

O241.82

A

1003-5060(2017)05-0712-04