基于低秩纹理变换不变性的车牌倾斜校正方法
许 超, 刘金阳, 凌 翔
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
基于低秩纹理变换不变性的车牌倾斜校正方法
许 超, 刘金阳, 凌 翔
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
文章提出一种适用范围更广的基于低秩纹理变换不变性的车牌倾斜校正方法。首先将车牌图像看成一个矩阵,然后利用对称规则结构的低秩特性把经过旋转、仿射等变换的图像恢复成低秩纹理。根据不同的环境条件,对随机拍摄的倾斜车牌图像进行校正,实验表明即使面对一些如无边框、车牌污染、环境光遮蔽、噪声大等恶劣条件,采用所提出的方法也得到了很好的校正结果。文中提出了一种借助于图像整体信息进行倾斜校正的新思路,该方法摒弃了以往考虑角点、边缘等局部特征的思路,具有更高的精确度和鲁棒性。实验结果证实所提出的方法是有效的,且满足整个识别系统的实时要求。
车牌;倾斜校正;低秩纹理;变换不变性;仿射变换
在自动车牌识别系统中,由于相机的角度变化,镜头的透视造成了图像在一定程度上不可避免地倾斜和变形,而且实际环境中天气情况不同、光照不均、车牌污染、车牌图像不完整等影响因素势必会对后续的字符分割和识别带来一定的负面影响。文献[1-2]利用霍夫变换(Hough transform,HT)对车牌图像进行直线检测,获取车牌的边框线条以确定倾斜角,最终得到车牌的校正图像;文献[3-4]对车牌图像进行旋转,将车牌上的像素点向坐标轴上投影,统计出每次旋转的最大值,取旋转投影最大值对应的角度为最终倾斜角度;文献[5]结合了霍夫变换与旋转投影,取得了一定的改进;文献[6]提出一种基于主成分分析(principle component analysis,PCA)的车牌图像畸变快速校正方法,将搜索图像倾斜角度转化为求取协方差矩阵的特征值和特征向量,简化了计算过程,提高了效率;文献[7-8]提出一种基于K-L变换(Karhunen-Loeve transform)的校正方法,该方法对特征空间分布的样本特征向量实行K-L变换,找到位数较少的组合特征,从而达到降低维度的目的,K-L变换本质上也属于PCA。这些方法都各有优点,同时也有一些局限性与不足之处。霍夫变换法需要对车牌图像进行多次边缘检测,但现实环境中获取的图像会由于噪声、光照、污染等原因,使得车牌边框不清楚甚至不存在,而且霍夫变换参数空间的峰值过于分散,因此使用霍夫变换法的校正效果并不理想;旋转投影法需要对车牌图像进行多次旋转投影,找到最佳倾斜角度,计算量较大;主成分分析法与前2类方法相比有很大的改进,却无法很好地校正错切变换后的图像。
低秩纹理变换不变性(Transform Invariant Low-rank Textures,TILT)[9]是矩阵低秩稀疏分解的一种推广。本文将其引入图像倾斜校正,提出一种基于低秩纹理变换不变性的车牌倾斜校正方法。TILT可用于提取二维图像中的低秩纹理,即使图像中存在严重的缺失或形变,TILT方法也能达到很好的预期效果,在经过合适的仿射或投影变换后,图像所对应的场景中有规则的模式尤其是具有某种对称性的纹理结构可以构成一个低秩矩阵,而遮蔽、污染等误差可以构成一个稀疏矩阵。实验表明,利用图像整体的低秩纹理结构建立数学模型,寻找最优变换恢复,可以提高图像倾斜校正的精确度和鲁棒性。
1 低秩纹理变换不变性
1.1 低秩纹理
一幅平面内的灰度图像可用数学表达式描述为一个二维函数f(x,y),将图像看成一个平面内的矩阵。在矩阵理论中,矩阵A的秩等价于A行向量(或列向量)的极大线性无关组中向量的个数。当矩阵的秩rank(A)≤k(其中k为较小的正整数)时,称该矩阵为低秩矩阵。低秩纹理则是满足低秩矩阵结构的图像场景。建筑物、文本、车牌、商标等符合或近似符合对称规则模式的物体表面图案称为具有低秩纹理,如图1所示;岩石、草地等物体表面图案具有随机性,可称之为随机纹理,如图2所示,通常这类纹理都是满秩的,故随机纹理不属于本文的讨论范畴。

图1 低秩纹理

图2 随机纹理
1.2 低秩纹理的变换与稀疏分解
在实际图像中,很难得到完美或近似完美的低秩纹理图像,主要有2个原因:
(1) 相机角度、镜头透视导致的倾斜变形。假设低秩纹理图像为A,观测得到的图像D一般不具有低秩纹理,若要将矩阵D恢复成具有低秩纹理的图像A,则需要有合适的逆转换τ,方程为:

其中,τ:R2→R2属于某一变换群,本文只讨论旋转、尺度、偏移变换,因此仅考虑仿射变换群。
(2) 噪声、环境光遮蔽和背景干扰等因素造成的像素采样值的变化。对这类因素可以引入稀疏误差矩阵E,表示为:
D=A+E。
2 车牌倾斜校正算法
2.1TILT数学模型的建立
假设D为原始观测图像矩阵,A为其低秩纹理部分,E为其稀疏误差。若要将D恢复出低秩部分A,则需要找到最优逆转换τ。因此根据TILT建立如下模型:

(1)
其中,‖E‖0为稀疏矩阵E非零元素的个数;λ为折中因子,且0≤λ≤1。
2.2TILT数学模型的求解
对于(1)式,交替方向方法[10]是目前较为流行的求解方法,为保证TILT中内循环理论上的绝对收敛和解决由奇异值分解带来的计算速度问题,本文采用自适应惩罚的线性化交替方向方法[11](Linearized Alternating Direction Method with Adaptive Penalty,LADMAP)和奇异值分解热启动[12]相结合的思路。
在 (1) 式中,由于矩阵秩和l0范数是离散的、非凸优化问题,属于NP难题,不能直接进行求解,因此将矩阵秩与l0范数分别转换成核范数[13]与l1范数[14],并对约束条件线性化[9],则目标函数可转变为:

(2)
其中,‖A‖*为矩阵A的核范数,即矩阵A的所有奇异值之和;‖E‖1为矩阵E所有元素绝对值之和;J为雅可比矩阵。
考虑到Δτ没有出现在目标函数内,因此当(A*,E*)满足最优化条件时,最优Δτ必将满足:
(3)
则(2)式可转变为:
(4)
其中,J⊥=I-J(JTJ)-1JT,且‖J⊥‖=1,(J⊥)T=J⊥,J⊥J⊥=J⊥;I为单位矩阵。
利用TILT模型求解车牌倾斜校正问题算法,即LADMAP算法,由外循环和内循环构成,具体如下所述。

输出:(A*,E*,τ*)。
初始化:A0=Dτ0,E0=0,Y0=0,i=0。
外循环:
(1) 图像规范化(包括灰度化、尺寸调整)和计算雅可比矩阵。
(2) 求解线性凸优化问题(5)式,即
(5)
初始值满足(6)式,即
(6)
执行内循环,即
k←k+1。
结束内循环直至满足迭代终止条件。

(4) 更新变换,即τi+1=τi+Δτ*,i←i+1。
结束外循环直至凸优化问题收敛。

(7)
(8)
其中,U为m阶正交矩阵,其列由XXT的特征向量组成;V为n阶正交矩阵,其行由XTX特征向量组成;Σ为m×n阶对角矩阵,对角元素为X的奇异值;Θ为收缩算子。
2.3TILT车牌图像校正算法实例
根据上述低秩纹理变换不变性原理以及求解算法,倾斜车牌图像的校正步骤大致可以归纳如下:
(1) 车牌图像以矩阵形式表示。首先对倾斜车牌图像灰度化,以像素(x,y)坐标为数据值,则一幅灰度车牌图像可表达为矩阵Dm×n,如图3所示。

图3 图像灰度化
(2) 根据TILT建立对应的模型并求解。建立(1)式模型,在约束条件下寻找最优逆变换τ,求解目标函数。其中内循环中A与E是通过交替的方式达到最优直至满足迭代条件,外循环是通过判断目标函数是否收敛来不断更新逆变换τ直至收敛。
(3) 获取结果。根据算法流程,实现图像的校正,得到最优逆变换τ,即

以及校正后低秩图像A和稀疏噪声E。TILT校正结果如图4所示。

图4 TILT校正结果
3 实验结果与分析
3.1 算法对比分析
由矩阵理论可知,矩阵的秩是该矩阵行向量(或列向量)的极大线性无关组向量的个数,矩阵中其他向量均可由该线性无关组线性表示,而且矩阵的秩与非零特征值的个数又有着密切的关系。图像处理领域中,图像矩阵并非都是方阵,因此通过矩阵奇异值分解中的奇异值来代替特征值。而那些小于η(也就是1/μk)的奇异值及其对应向量无需求出,原因是根据(8)式这些奇异值都被收缩为0,对Ak+1的值没有作用。由于惩罚因子μ与数据降维相关,初始值μ0的选取要尽可能适中。μ0不能太大,应该满足μ在前几次迭代就开始增长;μ0也不能太小,应尽可能满足μ随着迭代过程的进行稳步增长。本文μ0取值为:
其中,σmax(D)为D的最大奇异值。这样通过收缩算子Θ一方面可以降低数据维度,另一方面可以保留矩阵的有用信息。TILT模型正是基于图像矩阵的秩来建立的,而不是利用角点、边缘或其他局部特征,这样可以最大限度地获取图像已有的信息以及弱化噪声的干扰。同时只要原图像D本质上满足低秩纹理,在经过一系列的变换后,都将维持其原本的低秩特性,也就是低秩纹理图像A,因此倾斜车牌的校正并不依赖车牌中的字符内容,仅仅和原图像是否具有低秩特性(也就是图像是否符合或近似符合对称规则模式)有关。
采用霍夫变换法、旋转投影法以及主成分分析法校正倾斜的车牌图像时,都是通过获得最佳倾斜角度来校正图像,其根本上是对车牌图像作旋转变换,即
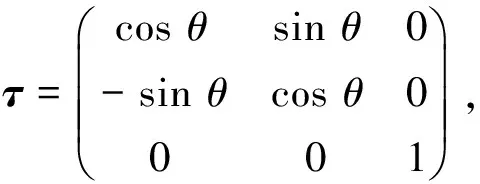
其中,θ为最佳倾斜角度。而大多数设备获取的车牌图像不仅会发生旋转,还或多或少会发生水平和/或垂直方向上的偏移,如图5所示。

图5 偏移图像旋转示例
也就是说车牌图像不仅发生旋转变换,而且有偏移变换,即
其中,sh为水平方向上的偏移;sv为垂直方向上的偏移。因此,仅以倾斜角度对图像作旋转就不能从根本上保证图像校正的准确性。本文TILT模型中将τ延伸至仿射变换,即使车牌图像在水平和/或垂直方向发生偏移也能获得较好的校正。
3.2 实验效果对比
选取随机拍摄的车牌图像300张,图像倾斜角度范围为(-π/6,π/6)且都有不同程度的偏移,车牌图像类型分布见表1所列。

表1 倾斜车牌图像分类个数
对这些图像采用霍夫变换法、旋转投影法、主成分分析法及本文基于TILT的方法在Matlab 8.3平台上进行求解,PC机的配置为Intel Core i5-2400 CPU@3.10 GHz,内存为4.00 GB,操作系统为Windows7(32位)。车牌图像倾斜校正对比如图6所示。由图6可见,本文方法获得了较好的校正结果。本文方法平均运行时间为0.12 s,满足车牌识别实时性要求。
需要特别指出的是,本文方法在车牌图像处于某些特殊条件下也可以获取不错的处理效果。图6a所示的原始图像并没有车牌边框的完整信息,图6d所示的车牌图像区域甚至字符处受到不同程度的污染,图6g所示为夜晚拍摄获取的图像,清晰度较低,噪声也较大,但通过本文方法都得到了较好的倾斜校正,由此可以得出本文方法具有较高的鲁棒性,其他3种方法均不能很好地校正发生偏移的车牌图像。

图6 车牌倾斜校正对比
4 结 论
从本文实验结果和分析中可以看出,用低秩纹理变换不变性(TILT)模型来校正倾斜车牌图像是一种行之有效的方法。该方法对噪声等一些不确定因素带来的干扰具有很强的鲁棒性,对于倾斜度较大、无边框、车牌污染的图像具有较好的处理效果;在运算速度方面,通过合理的程序优化,可以完全满足车牌识别中的实时要求。本文方法为利用图像整体信息进行倾斜校正提供了新思路。另外,本文方法也存在一些不足:① 仔细观察校正后的车牌图像可以发现,远距端车牌宽度小于近距端,这是由于在校正过程中未能考虑远近视距的深度信息,导致车牌呈现微梯形,今后将研究如何在校正过程中添加深度信息,例如,利用双目视觉获取图像深度等;② 倾斜校正的结果仅是从视觉效果上进行定性的评价,下一步将研究设计一种定量的评价标准。
[1] WEN C Y,YU C C,HUN Z D.A 3D transformation to improve the legibility of license plate numbers[J].Journal of Forensic Sciences,2002,47(3):578-585.
[2] 杨立刚,张兴会,李兰友.车牌照字符倾斜校正方法的研究[J].仪器仪表学报,2004,25(4):696-697.
[3] 李文举,梁德群,崔连延,等.一种新的车牌倾斜校正方法[J].信息与控制,2004,33(2):231-235.
[4] 吴丽丽,余春艳.基于Sobel算子和Radon变换的车牌倾斜校正方法[J].计算机应用,2013,33(增刊1):220-222.
[5] DENG H Y,ZHU Q X,TAO J S,et al.Rectification of license plate images based on Hough transformation and projection[J].Indonesian Journal of Electrical Engineering and Computer Science,2014,12(1):584-591.
[6] 吴德会,朱程辉.基于主元分析的车牌图像倾斜校正新方法[J].公路交通科技,2006,23(8):143-146.
[7] 吴一全,丁坚.基于K-L展开式的车牌倾斜校正方法[J].仪器仪表学报,2008,29(8):1690-1694.
[8] PAN M S,XIONG Q,YAN J B.A new method for correcting vehicle license plate tilt[J].International Journal of Automation and Computing,2009,6(2):210-216.
[9] ZAHNG Z D,GANESH A,LIANG X,et al.TILT: transform invariant low-rank textures[J].International Journal of Computer Vision,2012,99(1):1-24.
[10] 史加荣,郑秀云,魏宗田,等.低秩矩阵恢复算法综述[J].计算机应用研究,2013,33(6):1601-1605.
[11] LIN Z C,LIU R S,SU Z X.Linearized alternating direction method with adaptive penalty for low-rank representation[C]//Proceedings of the Neural Information Processing Systems Conference.Granada,Spain:[s.n.],2011:612-620.
[12] WEN Z W,YIN W T.A feasible method for optimization with orthogonality constraints[J].Mathematical Programming,2013,142(1/2):397-434.
[13] CANDES E J,LI X D,MA Y,et al.Robust principal component analysis?[J].Journal of the ACM,2011,58(3):1-37.
[14] DONOHO D L.For most large underdetermined systems of linear equations the minimall1-norm solution is also the sparsest solution[J].Communications on Pure and Applied Mathematics,2006,59(6):797-829.
(责任编辑 张淑艳)
Vehicle license plate tilt correction approach based on transform invariant low-rank textures
XU Chao, LIU Jinyang, LING Xiang
(School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China)
A vehicle license plate tilt correction approach based on transform invariant low-rank textures is proposed, which has a wider range of applications. Firstly, considering the license plate image as a matrix, the low-rank characteristic of regular structures and symmetric patterns is utilized to restore the image undergoing rotation and affine transformation into a low-rank textures. According to different environmental conditions, the tilt correction for license plate images which are randomly shot is carried out. Experimental results show that even in the face of some harsh conditions, such as borderlessness, pollution, ambient occlusion and image noise, excellent correction results are obtained by the proposed method. A new idea of tilt correction by means of the image overall information is put forward, which abandons the previous point of view from the corner, edge and other local features, and therefore it has a higher robustness and accuracy. Experimental results demonstrate that the proposed method is effective and can satisfy the demands of the whole vehicle license plate recognition system in real time.Key words:vehicle license plate; tilt correction; low-rank texture; transform invariance; affine transform
2015-10-28;
2016-03-18
许 超(1991-),男,安徽芜湖人,合肥工业大学硕士生; 凌 翔(1983-),男,安徽宣城人,博士,合肥工业大学副教授,硕士生导师.
10.3969/j.issn.1003-5060.2017.05.012
TP391.41
A
1003-5060(2017)05-0633-05

