一种改进的Kron形式子结构模态综合法
崔 杰,王光远,郑钢铁
(1. 清华大学航天航空学院,北京100084;2. 北京空间飞行器总体设计部,北京100094)
一种改进的Kron形式子结构模态综合法
崔 杰1,王光远2,郑钢铁1
(1. 清华大学航天航空学院,北京100084;2. 北京空间飞行器总体设计部,北京100094)
基于Kron形式子结构方法提出一种近似自由界面子结构模态综合法(Component modal synthesis, CMS)。为提高求解精度,在不提高缩减系统特征方程阶数的情况下,将自由界面剩余附着模态的惯性贡献引入了Kron形式CMS方法。同时,对广义坐标按照频域贡献进行了凝聚,以降低最终缩减模型的维数。数值算例的结果表明,当截断准则相同时,该方法计算量与传统的基于静态近似的CMS方法基本一致,但求解精度显著提高,因此计算效率更高。
结构动力学;模型缩减;子结构模态综合;动力子结构方法;Kron形式子结构方法
0 引 言
模态参数可以表征系统低频段的动力学特性,是结构设计中的重要参考指标。现代航天器结构的有限元(Finite element, FE)模型常包含大量的自由度[1-2],同时,在设计、分析过程中往往需要对模型进行大量的修改与调整。考虑到设计周期的限制,这便对计算效率提出了很高的要求。模型缩减是结构动力学中广泛应用的方法,其目的在于以尽可能少的精度损失提高计算效率[3-5]。
子结构模态综合法(Component modal synthesis, CMS)是一种常用的模型缩减方法[4-6],其将整体复杂结构的模型缩减问题分解为部件级别的模型缩减。因此,计算效率可以得到极大提高。近年来,其在汽车[6-7]、卫星[8]、火箭[9]、转子[10]系统等领域有着广泛的应用。CMS方法中主要包括固定界面CMS法[11-13](Craig-Bampton, C-B法)及自由界面CMS法[14-16]两类。两类方法各有特点,其中固定界面法中广义坐标必须包括界面自由度的物理坐标,而自由界面法可以仅选用模态坐标作为广义坐标,因此后者得到的缩减模型维数更低,尤其是当有限元模型的网格密度较大时。此外,自由界面法采用的边界条件与试验状态更为接近,便于结合实验进行修正和验证[17-18]。因此,本文着眼于自由界面法。
自由界面CMS方法中,Kron形式的CMS法通过连接矩阵及独立界面力来表达子结构间的连接关系,具有数学表述简单、便于处理大量子结构通过复杂拓扑关系连接的情况等优点。最近,Weng等[19]对此方法进行了改进,将自由界面剩余附着模态引入Kron形式CMS方法,极大地提高了其计算效率与工程适用性。但是,方法中对剩余附着模态进行了静态近似,因此精度损失较大。一般工程问题中,综合考虑求解精度与计算效率,计算时应考虑剩余项的惯性贡献[20-21]。
本文对Weng等[19]的方法进行改进,进行截断补偿时考虑剩余附着模态的惯性贡献。其中的主要问题有两点:1)剩余附着模态为待求整体结构特征值的函数,一般通过级数展开进行近似,当保留项数大于一时,子结构缩减系统的特征方程为非线性特征方程,需要迭代求解,这反而可能降低计算效率;2)Weng等[19]方法的缩减系统广义坐标中包含独立界面力,这提高了缩减系统的维数。针对第一个问题,本文采用O’Callahan[20]将惯性贡献引入Guyan凝聚[22]的方法,即采用静态近似得到的缩减系统特征对来近似精确剩余附着模态中未知的整体结构特征对。这样,对剩余附着模态进行惯性近似后,模态变换矩阵为常数矩阵,因此最终得到的缩减系统特征方程仍为线性特征方程。对第二个问题,文中对静态近似后缩减系统的广义坐标按照其频域贡献进行凝聚,以降低最终缩减系统的维数,这一思路源于多尺度子结构方法中的界面广义坐标缩聚[21]。与改进前的方法相比,本文提出的方法在不提高缩减系统特征方程阶数的情况下引入了惯性近似且最终缩减系统维数更低,因此计算效率更高。
1 Kron形式CMS方法回顾
1.1 传统Kron形式CMS方法
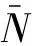
(1)
式中:约束前的整体结构刚度及质量矩阵分别由Kdiag(K(1),…,K(n))及Mdiag(M(1),…,M(n))表示为整体结构模态,C为表示子结构间连接关系的连接矩阵,τk为与对应的独立界面力矢量[4,19]。
(2)
式中:ΛL
ΦL
ΛH
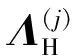
ΦH
ΓLCΦL,ΓHCΦH
(3)

为进行截断补偿,引入自由界面剩余附着模态,由式(2)第二行可得:
(4)
将式(4)代入式(2)可消去坐标ηk,即:
(5)
其中,
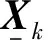
(6)
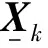
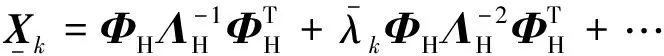
(7)
式中:F为子结构剩余柔度。为简化计算,忽略级数高阶项对的贡献,仅保留前两项,即假设式(5)可化为:
(8)
其中
k
qk
(9)
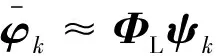
1.2 CKC法讨论:近似阶数
从数学的角度,模态综合法是一种Ritz法,模态变换矩阵为Ritz基。CKC法缩减系统(k,m)满足如下关系:
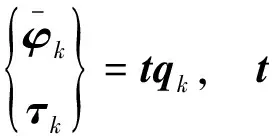
(10)
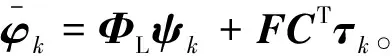
基于动力凝聚法[20]及C-B法[21]研究结论,对剩余项进行近似时考虑其惯性贡献计算效率更高。因此,本文通过在模态变换t中引入剩余附着模态的二阶近似来改善CKC法效率,其关键在于引入惯性影响的同时不提高缩减系统特征方程的阶数。
2 改进的Kron形式CMS方法
本节给出改进的Kron形式CMS(Enhanced Kron’s CMS, EKC)方法的推导过程。在CKC法的基础上,其主要包含广义坐标缩减及剩余附着模态惯性近似两步。
2.1 广义坐标缩减
CKC法缩减系统的维数为nCKC=nKC+NICF,其中NICF为独立界面力的个数(或C的行数)。注意到NICF个独立界面力坐标对应非特征向量,而nKC个子结构模态坐标中亦有部分坐标对应分析频带外的模态。因此,为提高计算效率,首先对缩减模型广义坐标进行缩减,仅求解分析频带内的模态。
在求解特征方程式(8)后,广义坐标qk可以表示为:
(11)
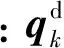

(12)
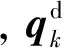
考虑凝聚变换式(13)后,式(8)化为:
(13)
其中,k=1,2,…,nEKC且
(14)
这样,缩减系统特征方程由nCKC维缩减至nEKC维,同时分析频带内模态的精度仍能得到保证。
2.2 剩余附着模态惯性近似
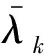
首先,注意到广义坐标缩减变换式(13)及一阶近似模态变换式(11),式(16)可近似表示为:
(16)
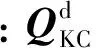
然后,由式(14)可知:
(17)
最后,将式(18)代入式(17)可得:
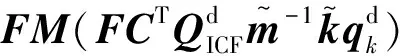
(18)
式中:TEKC为EKC法对应的模态变换矩阵,对应的缩减系统特征方程为:
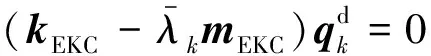
(19)
2.3 算法实现及讨论
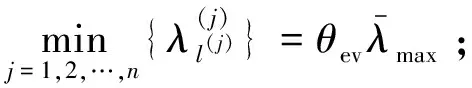
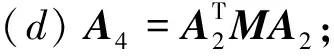
步骤3:(a) 组装:
(20)
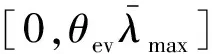
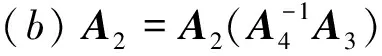
上述EKC法中,步骤1~3为CKC法。从编程角度,步骤1~5需考虑如下注释:
注1.关于系数因子θev,步骤1(b)中θev一般应大于1.5[23];步骤3(b)中θev值可与步骤1(b)中的不同,应保证nEKC≤nKC,推荐nEKC=(1.5~2)nd,nd分析频带内整体结构模态数,可通过步骤3(b)估计。
注2.矩阵C(或C(j))为符号布尔矩阵,只有每个子结构界面处元素为1或-1,其余均为0。因此与C相关的矩阵乘法运算可通过直接组装实现。
注3.注意到关系
(21)
且K为稀疏矩阵,因此需采用“分解-回代”的方式实现与F相关的乘法。当划分后存在自由子结构时,K不可逆,此时可使用惯性释放方法去除K中的刚体模态分量[14]。
EKC法与CKC法的计算量主要由行(或列)维数为N(j)的矩阵的运算决定。对第j个子结构:
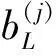
3 数值算例
本节通过两个算例,即Euler-Bernoulli梁及某卫星主动段模型,来比较EKC法及CKC法的精度及效率,两种方法按第2.3节所述算法实现,计算机配置为:Windows7-64bit系统、4核Intel Core处理器及24GB内存。对于Euler-Bernoulli梁,为便于实现及对照,算法基于MATLAB 2012b实现。对于卫星模型,算法使用Nastran的二次开发语言Direct Matrix Abstraction Program(DMAP)实现。
3.1 Euler-Bernoulli梁


图1 Euler-Bernoulli梁模型及其子结构划分
Fig.1 Euler-Bernoulli beam model and its components
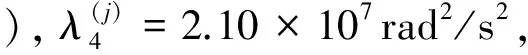
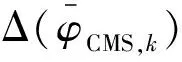
(22)
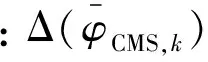
由表1可知,在分析频带内,EKC法精度比CKC法高出两个数量级,这是由于EKC法在对剩余附着模态进行截断时考虑了其惯性影响。对于EKC法,进行广义坐标减缩后,精度略微下降,但仍远高于CKC法。高阶模态的精度较低阶模态下降的更明显,由于缩减时忽略的广义坐标对应的模态所属频带与高阶模态所属的频带更为接近。
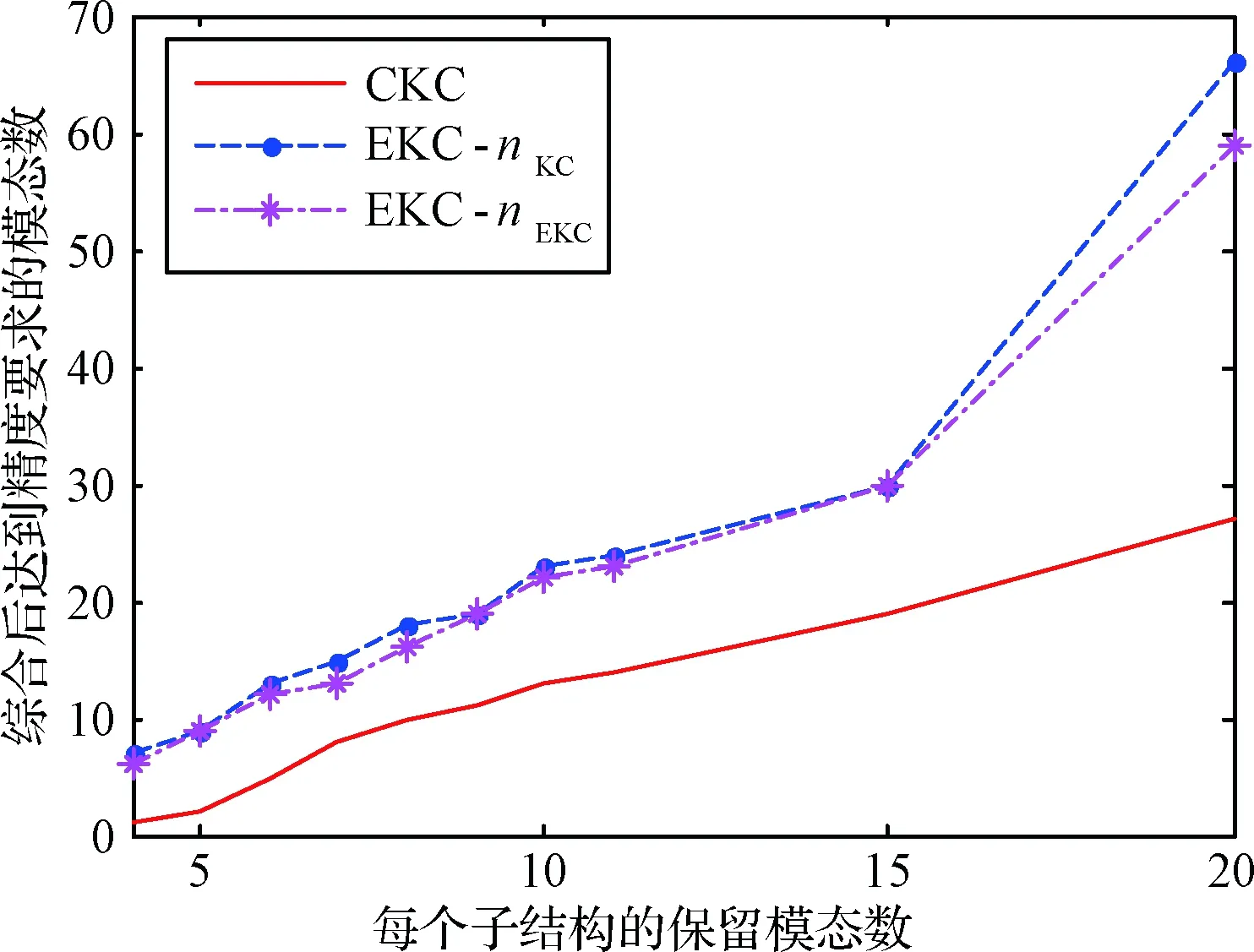
图2 EKC法及CKC法模态收敛性比较Fig.2 Modal convergence of the EKC and CKC methods
进一步比较上述近似子结构方法的模态收敛性,即:随子结构保留模态的增加,综合后达到给定精度要求的整体系统模态数的变化。这里精度要求取特征值相对误差为1×10-6,广义坐标缩减时仍取θev=1。结果如图2所示,其中曲线“CKC”、“EKC-nKC”及“EKC-nEKC”分别对应CKC法、选取nKC及nEKC阶主导广义模态的EKC法结果。由图2可知,EKC法模态收敛性优于CKC法,尤其是在低频段,即子结构保留模态较少时;同时广义坐标缩减对EKC法模态收敛性影响较小。
3.2 某卫星模型
本节通过某型卫星主动段FE模型来进一步验证EKC法在实际工程应用中的精度与效率。如图3所示,此模型按照实际卫星方案阶段配置建立,单元类型统计见表2,共1602122自由度,星箭转接框处固支。按照不同模块在连接处将其划分为10个子结构,相关矩阵维数见表3。
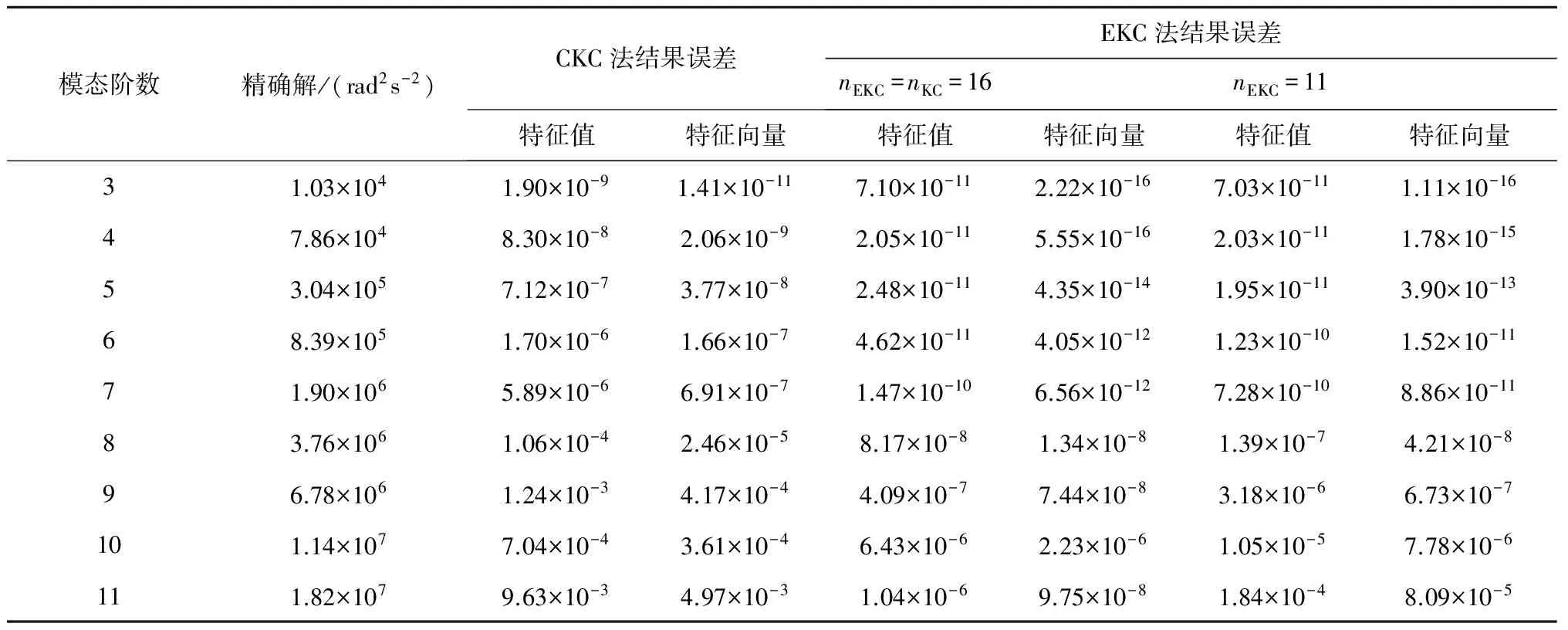
表1 Euler-Bernoulli梁算例结果Table 1 Results of the Euler-Bernoulli beam model

表2 卫星有限元模型构成Table 2 Summary of the satellite FE model
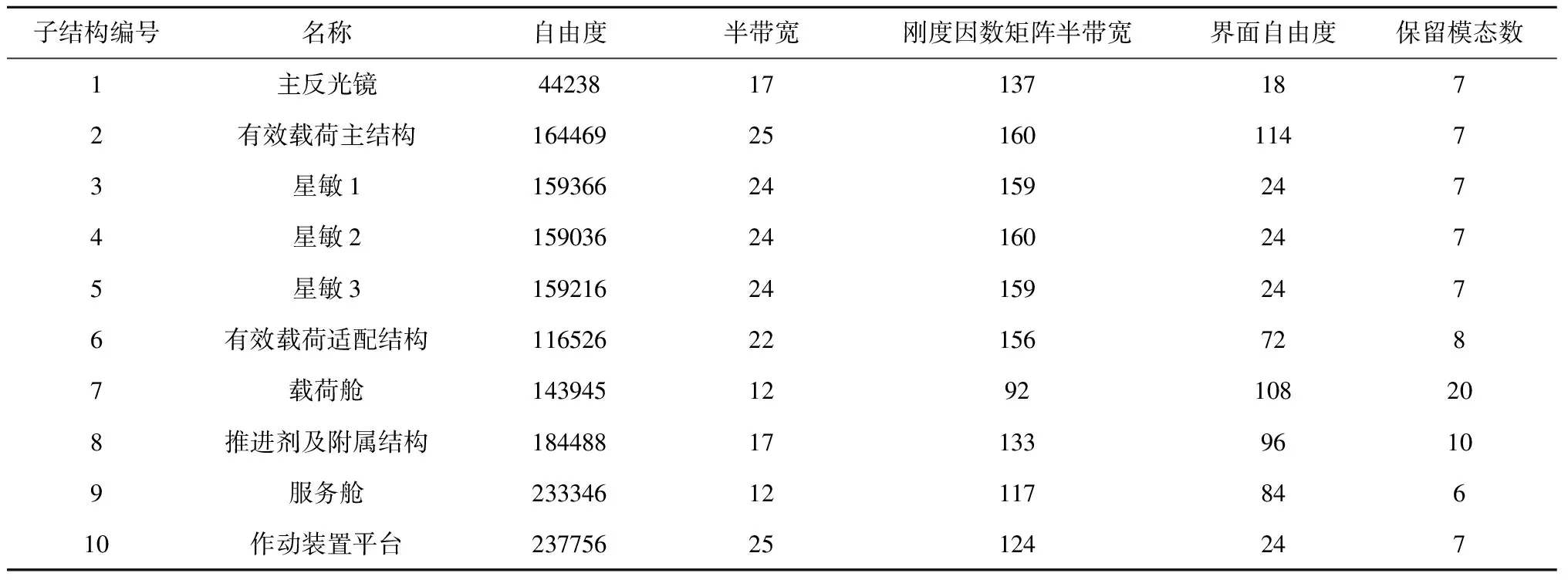
表3 卫星模型子结构划分参数Table 3 Matrix size of the CMS methods for the satellite
假定需求解卫星前10阶模态,对应主动段载具外激励主导分量所处频带。求解时EKC及CKC法采用同样的截断准则,即步骤1(b)中θev≈2,对应子结构保留模态数见表3。注意到此时nKC=86远大于所需整体模态数。为比较界面力减缩影响,按照注释1所述准则,分别考虑nEKC=nKC=86及nEKC=16两种情况。计算精度见表4,其中特征值及特征向量相对误差定义与第3.1节中定义一致。
由表4可知,在分析频带内,EKC法精度远高于CKC法。对于EKC法,考虑广义坐标凝聚后,精度略微下降,其中高阶模态的精度下降的更明显。
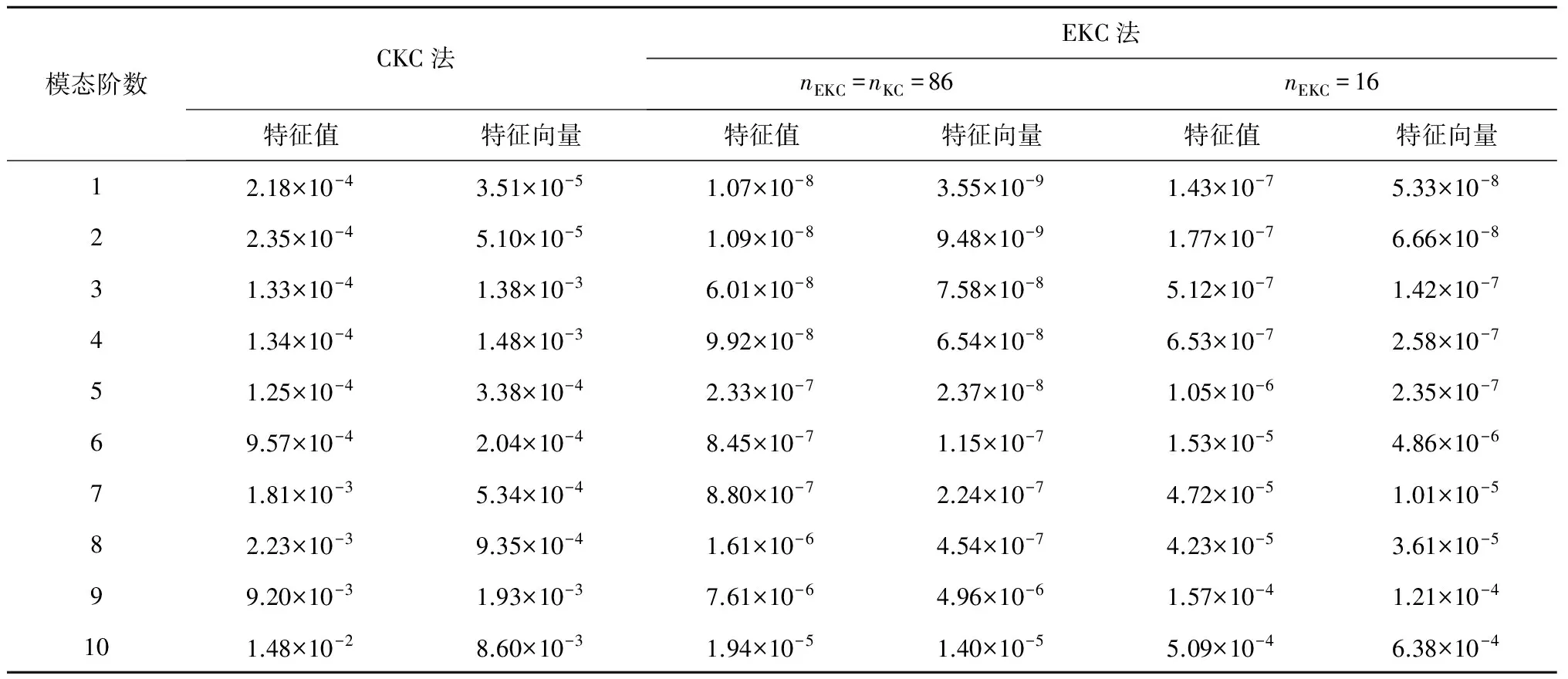
表4 卫星模型计算误差Table 4 Error of different CMS methods for the satellite
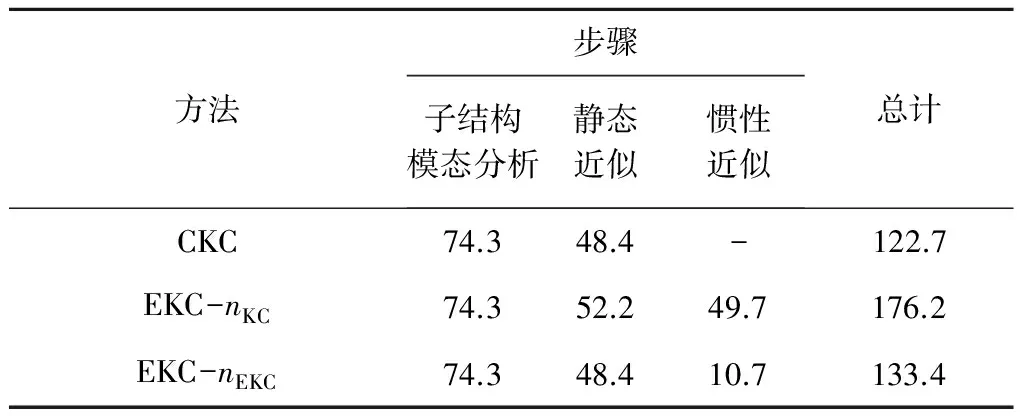
表5 卫星模型CPU运行时间(s)统计Table 5 CPU time(s) for the satellite
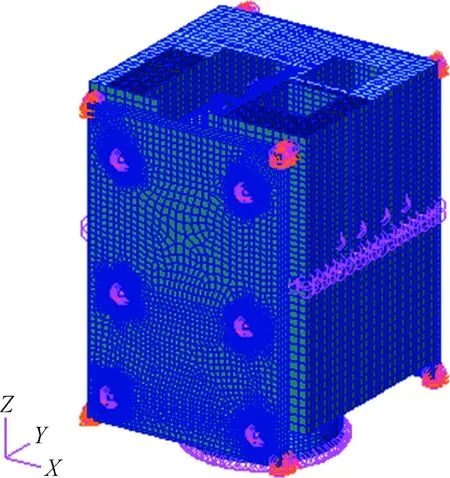
图3 卫星主动段模型Fig.3 Launch phase model of a satellite
为分析计算效率,将两种子结构方法主要步骤所需的计算时间列于表5,表中子结构模态分析对应步骤1,静态近似对应步骤2、3,惯性近似对应步骤4、5。分析表5可知:
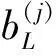
2)广义坐标缩减后,惯性近似额外所需的时间减少为原来的21.5%,仅为CKC法所需时间的8.7%,而此时计算精度相比CKC法提高近两个数量级,这说明了广义坐标缩减的有效性;
综上所述,本文提出的EKC法适用于实际复杂工程问题,且效率比传统的CKC法更高。
4 结 论
本文提出了一种改进的Kron形式CMS方法。首先,在模态变换中考虑了剩余附着模态的惯性贡献,因此在相同的模态截断准则下,可以得到更高精度的模态。特别的,引入惯性近似后,本方法的缩减系统特征方程仍为线性。同时,为降低最终缩减模型的维数,对广义坐标按照其频域贡献进行凝聚。这样,相比传统Kron形式CMS方法,本方法可以更高效地求解系统的模态参数。文中通过实际工程算例验证了本方法的有效性。
[1] Wei F, Zheng G T. Nonlinear vibration analysis of spacecraft with local nonlinearities [J]. Mechanical System and Signal Processing, 2010, 24: 481-490.
[2] Liu M H, Zheng G T. Component synthesis method for transient response of nonproportionally damped structures [J]. AIAA Journal, 2010, 48 (11): 2556-2563.
[3] Besselink B, Tabak U, Lutowska A. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control [J]. Journal of Sound and Vibration, 2013, 332: 4403-4422.
[4] de Klerk D, Rixen D J, Voormeeren S N. General framework for dynamic substructuring: history, review, and classification of techniques [J]. AIAA Journal, 2008, 46(5): 1169-1181.
[5] 向树红, 邱吉宝, 王大均. 模态分析与动态子结构方法新进展 [J]. 力学进展, 2004, 34(3): 289-303. [Xiang Shu-hong, Qiu Ji-bao, Wang Da-jun. The resent progresses on modal analysis and dynamic substructure methods [J]. Advances in Mechanics, 2004, 34(3): 289-303.]
[6] 应广驰, 孟光, 龙新华, 等. 用自由界面模态综合法研究发动机—排气管—涡轮增压器系统的振动 [J]. 机械与强度, 2010, 32(1): 10-16. [Ying Guang-chi, Meng Guang, Long Xin-hua, et al. Study on engine-manifold-turbocharger system’s vibration by free interface modal synthesis method [J]. Journal of Mechanical Strength, 2010, 32(1): 10-16.]
[7] 李英强. 基于模态综合的汽车结构优化研究 [D]. 重庆: 重庆大学, 2012. [Li Ying-qiang. Study on automotive structural optimization based on component mode synthesis [D]. Chongqing: Chongqing University, 2012.]
[8] 史纪鑫, 曲广吉. 可变构型复合柔性结构航天器动力学建模研究 [J]. 宇航学报, 2007, 28(1): 130-135.[Shi Ji-xin, Qu Guang-ji. Mathematical modeling of a class of variable structure spacecraft with flexible multibody appendages [J]. Journal of Astronautics, 2007, 28(1): 130-135.]
[9] 章敏, 蔡国平. 捆绑式运载火箭的模型降阶 [J]. 宇航学报, 2010, 31(5): 1317-1321. [Zhang Min, Cai Guo-ping. Model reduction of a strap-on launch vehicle [J]. Journal of Astronautics, 2010, 31(5): 1317-1321.]
[10] 陈海卫, 张秋菊, 曹毅. 波轮式全自动洗衣机刚柔耦合模型的建立 [J]. 振动与冲击, 2012, 31(15): 185-189. [Chen Hai-wei, Zhang Qiu-ju, Cao Yi. Flexible model for a vertical axis automatic washing machine [J]. Journal of Vibration and Shock, 2012, 31(15): 185-189.]
[11] Craig R R, Bampton M C C. Coupling of substructures for dynamic analysis [J]. AIAA Journal, 1968, 6(7): 1313-1319.
[12] 王缅, 郑钢铁. 一种改进的固定界面模态综合法[J].宇航学报, 2012, 33(1): 291-297. [Wang Mian, Zheng Gang-tie. An improved fixed-interface modal synthesis method [J]. Journal of Astronautics, 2012, 33(1): 291-297.]
[13] 诸赟, 张美艳, 唐国安. 一种基于子结构界面动刚度的模态综合法 [J]. 振动工程学报, 2015, 28(3): 345-351. [Zhu Yun, Zhang Mei-yan, Tang Guo-an. A modal synthesis method based upon dynamic stiffness on interface [J]. Journal of Vibration Engineering, 2015, 28(3): 345-351.]
[14] Craig R R, Chang C J. On the use of attachment modes in substructure coupling for dynamic analysis [C].The 18th Structures, Structural Dynamics and Material Conference, AIAA Paper, 1977, 77-405.
[15] 王缅. 有限元动力学宽频带计算与连接结构实验建模方法研究 [D]. 北京:清华大学, 2011. [Wang Mian. Broadband dynamic computation and experimental connection modelling with finite element method [D]. Beijing: Tsinghua University, 2011.]
[16] 楼梦麟, 唐玉. 基于节点力插值的自由子结构界面自由度缩减方法 [J]. 同济大学学报自然科学版, 2015, 43(5): 662-667. [Lou Meng-lin, Tang Yu. Degrees of freedom reduction technique for free-interface substructure based on nodal force interpolation [J]. Journal of Tongji University (Natural Science), 2015, 43(5): 662-667.]
[17] 邱吉宝, 王建民. 运载火箭模态试验仿真技术研究新进展 [J]. 宇航学报, 2007, 28(3): 7-13. [Qiu Ji-bao, Wang Jian-min. The recent progresses on research into modal test simulation techniques for launch vehicles [J]. Journal of Astronautics, 2007, 28(3): 7-13.]
[18] 杜飞平, 谭永华, 陈建华, 等. 航天器子结构模态综合法研究现状及进展 [J]. 火箭推进, 2010, 36(3): 39-44. [Du Fei-ping, Tan Yong-hua, Chen Jian-hua, et al. Status and progress on substructural modal synthesis techniques for space vehicles [J]. Journal of Rocket Propulsion, 2010, 36(3): 39-44.]
[19] Weng S, Xia Y, Xu Y L. Improved substructuring method for eigensolutions of large-scale structures [J]. Journal of Sound and Vibration, 2009, 323(3-5): 718-736.
[20] O’Callanhan J. A procedure for an improved reduced system (IRS) model [C]. Proceedings of the 7th International Modal Analysis Conference, Bethel CT, 1989: 7-12.
[21] Kim J G, Boo S H, Lee P S. An enhanced AMLS method and its performance [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 287: 90-111.
[22] Guyan R J. Reduction of stiffness and mass matrices [J]. AIAA Journal, 1965, 3: 380.
[23] Rubin S. Improved component-mode representation for structural dynamic analysis [J]. AIAA Journal, 1975, 13(8): 995-1006.
通信地址:北京市清华大学蒙民伟科技大楼N604室(100084)
电话:(010)62783235
E-mail: j-cui12@mails.tsinghua.edu.cn
An Enhanced Kron’s Component Modal Synthesis Method
CUI Jie1, WANG Guang-yuan2, ZHENG Gang-tie1
(School of Aerospace Engineering, Tsinghua University, Beijing 100084, China;Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)
A new free-interface component modal synthesis (CMS) method is developed in this paper based on the Kron’s substructuring. For better precision, the inertia approximation of the residual attachment modes, which depends on the unknown global eigenvalues by definition, is included in the modal transformation matrix while the reduced system eigen-equation is still linear. Moreover, the generalized coordinates are further condensed to reduce the size of the reduced model. Compared with the conventional static-approximated CMS methods, the precision is significantly improved with little additional computational cost. Numerical examples validate the precision and efficiency of the proposed method.
Structural dynamics; Model reduction; Component modal synthesis; Dynamic substructuring; Kron’s substructuring
2017-03-14;
2017-04-25
V414.1
A
1000-1328(2017)06-0566-08
10.3873/j.issn.1000-1328.2017.06.002
崔 杰(1989-),男,博士生,主要从事航天器结构动力学,振动与控制方面的研究。

