考虑成像质量的敏捷卫星任务调度模型与算法

李志亮，李小将，孙 伟

(1. 装备学院研究生院，北京101416；2. 装备学院航天装备系，北京101416；3. 北京航空航天大学仪器科学与光电工程学院，北京100191)



考虑成像质量的敏捷卫星任务调度模型与算法

李志亮1，李小将2，孙 伟3

(1. 装备学院研究生院，北京101416；2. 装备学院航天装备系，北京101416；3. 北京航空航天大学仪器科学与光电工程学院，北京100191)

针对敏捷卫星任务调度中成像质量受观测时间影响的特点，构建考虑观测时间因素的约束满足模型，提出一种将离散差分进化与变邻域搜索相结合的求解算法(DDE-VNS)。首先，描述敏捷卫星任务调度时间约束；其次，考虑观测时间对成像质量的影响、任务间姿态转换时间约束、星上存储与能量约束等因素构建了敏捷卫星任务调度的约束满足模型；再次，设计离散差分进化的变异、交叉和选择算子，采用变邻域搜索对每次迭代的最优解进行局部搜索以寻找更好的邻域解，并给出了算法的实现流程。仿真结果表明,利用该模型可获得收益值较高的调度方案，且该算法在收敛速度更有优势。

敏捷卫星；任务调度；离散差分进化；变邻域搜索

0 引 言

敏捷卫星是指有效载荷固定于卫星平台，依靠姿态轨道控制系统实现滚动、俯仰和偏航三个轴向快速机动的卫星[1]。相比于传统成像卫星，敏捷卫星姿态机动能力更强、观测时间窗口更长、任务冲突的解决方式更多，单次过境的任务执行能力大大增强。目前，各航天大国已研制发射了多颗敏捷卫星，如美国的WorldView系列卫星、法国的Pleiades星座、以色列的EROS-B卫星。敏捷卫星在军事侦察、抗震救灾等任务中能够发挥分散目标快速成像、复杂任务高效执行、不确定因素有效应对等优势，具有广阔的应用前景，是新型卫星发展的重要方向。

敏捷卫星潜在的优势依赖于有效的调度模型和算法。文献[1]认为敏捷卫星灵活机动优势带来的观测时间不确定性使得该问题兼具选择和调度特性，考虑单星单轨构建了数学规划模型，并分析了贪婪搜索、动态规划、约束规划和局部搜索等算法的求解效率。文献[2]构建了考虑任务间姿态转换、星上存储和能量等约束的数学模型，设计了一种混合遗传算法进行求解。文献[3]通过改变种群迭代次序提出一种基于二进制指标的多目标局部搜索算法，计算结果表明该方法在运算方面更为高效。文献[4]分析了敏捷卫星成像几何模型和时间模型，提出一种条带划分和时间窗口求解算法。文献[5]考虑时间窗口、星上存储和最长连续工作时间约束构建了数学规划模型，提出一种评价调度收益和资源消耗的优先级指标，并根据该指标设计了蚁群优化算法。文献[6]基于复杂网络理论研究了单星调度问题，将每个节点作为目标的观测机会，提出节点和目标的重要性指标，并设计了一种近似求解算法。

通过社会协作、自我适应和竞争实现进化的群体智能算法是解决多约束组合优化问题的有效方法[7]。差分进化(Differential evolution, DE)算法是由Store和Price[8]提出的一种基于群体智能的优化算法，它采用实数编码、基于差分的简单变异操作和一对一的竞争策略，具有较强的全局搜索能力。文献[9]提出一种求解流水车间调度问题(Flow shop scheduling problem，FSP)的离散差分进化(Discrete differential evolution, DDE)算法，该算法通过取模运算改进变异算子。文献[10]基于标度法和层次分析法研究了自适应离散差分进化算法的候选解产生策略选择问题。文献[11]将DDE算法用于求解武器-目标分配(Weapon-target assignment，WTA)问题。文献[12]针对信号采集卫星系统的调度问题，提出一种基于二次映射编码的动态调度差分进化算法。

上述研究为敏捷卫星任务调度建模和求解提供了很好途径。同时存在一些不足，文献[1]忽略了星上存储和能量约束，并且将姿态转换时间作为固定值进行了简化，带来任务间存在时间冲突的问题。文献[2-6]将最大化完成任务的优先级之和作为目标函数，没有考虑敏捷卫星观测时间对成像质量的影响，文献[13]基于敏捷成像模型分析了多因素影响下的成像质量评价准则，但是没有研究考虑成像质量的调度问题。文献[9-12]的研究为差分进化求解组合优化问题提供了较好的思路，同时，由于编码方式和辅助算子不同，变异和交叉操作容易产生不合理的个体编码，其应用扩展性有限。

针对以往研究的不足，本文在描述敏捷卫星任务调度时间约束的基础上，综合考虑观测时间对成像质量的影响、任务间姿态转换约束、星上存储和能量约束等，通过改进目标函数建立了调度约束满足模型，提出一种将离散差分进化与变邻域搜索相结合的算法(Discrete differential evolution with variable neighborhood search, DDE-VNS)，通过仿真算例校验了模型的有效性和算法优越性。

1 敏捷卫星任务调度时间约束描述

姿态机动能力增加了敏捷卫星对地观测的自由度，同时，其任务调度的时间约束变得更加复杂，主要体现在成像、姿态转换方面。在成像活动中，当一个地面目标被选定后，其观测时间是可见时间窗口内的一个连续变量，不同观测时间对应的观测姿态角不同，观测姿态角直接影响卫星对地面目标的成像分辨率，而成像分辨率是成像质量好坏的主要评价指标，因此，观测时间影响卫星对地面目标的成像质量。此外，在姿态转换活动中，对于相邻任务，卫星需完成任务间的姿态转换，姿态转换时间取决于前后任务的结束和开始时间，当卫星资源有限而成像任务众多时，姿态转换时间主要受前一任务的结束时间影响，选择不同的时间进行姿态转换，所需转换时间也不同。

基于一般化的时间约束问题，敏捷卫星任务调度时间约束可以描述为：设一组变量集合X={X1,X2,…,Xn}和一组变量上的约束C={C1,C2,…,Cn}，其中每个变量代表一次成像活动的时间点，变量上的约束代表成像活动的时间窗口约束以及前后相邻活动间的姿态转换约束，当赋值{X1=a1,X2=a2,…,Xn=an}满足所有约束时，称X={a1,a2,…,an}为该时间约束的解。对于所有可行解，每个活动的时间赋值在一定区间范围内，不同的时间赋值即不同的观测时间，对应的成像质量不同。因此，这种时间赋值是调度方案优劣的直接体现，敏捷卫星任务调度中，需要考虑这种时间赋值对调度方案的影响。

2 敏捷卫星任务调度约束满足模型

首先定义建立调度约束满足模型所需参数，然后从决策变量、目标函数、约束条件3个方面描述模型。

2.1 参数定义

本文模型相关参数定义如表1所示。

表1 相关参数定义Table 1 Definition of related parameters

2.2 模型描述

针对文献[1]简化姿态转换约束的不足，本文通过计算不同时刻下卫星对地面目标的观测姿态角，确定姿态机动时间，使任务间姿态转换约束更为合理。针对文献[2-6]的研究均没有考虑观测时间对成像质量影响的不足，本文在目标函数中增加成像质量评价函数，根据任务优先级和观测时间确定目标函数值。考虑上述改进的目标函数和增加的约束条件，多敏捷卫星任务调度的约束满足模型描述如下：

1)决策变量

2)目标函数

在以往对敏捷卫星任务调度的研究中，常见的目标函数是最大化完成任务的优先级之和[2-6]，其描述如下式：

(1)

敏捷卫星对地面目标的观测时间是可见时间窗口内的一个连续变量，观测时间离可见时间窗口的中心时刻越近，对应的观测姿态角越小，成像质量也越好；反之离中心时刻越远，对应的观测姿态角越大，成像质量则越差。在敏捷卫星任务调度模型中考虑观测时间对成像质量的影响，通过合理安排任务的观测时间提高成像质量，具有一定的现实意义。

当采用P1作为目标函数，且任务ti被选择观测时，无论任务ti的观测时间处于其可见时间窗口内的哪一时刻，计算所得目标函数值均为wi，而实际上，卫星在不同观测时间对目标的成像质量有一定差异。因此，有必要构建观测时间与成像质量之间的函数关系式。

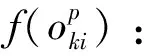
(2)

(3)

(4)

(5)

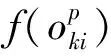
3)约束条件

本文模型考虑以下5方面的约束条件：

(1)任务执行的唯一性约束

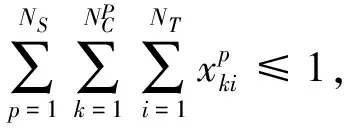
(6)

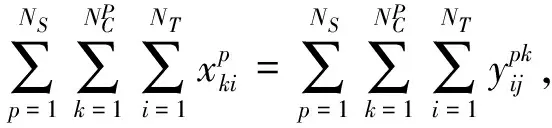
(7)

(2)任务执行的时间窗口约束

(8)

(3)相邻任务间姿态转换时间约束

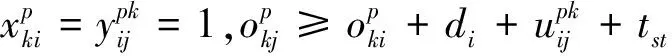
(9)

(4)卫星单个轨道圈次的存储约束

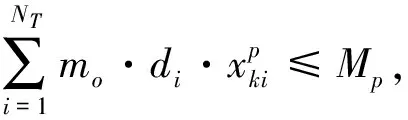
(10)

(5)卫星单个轨道圈次的能量约束

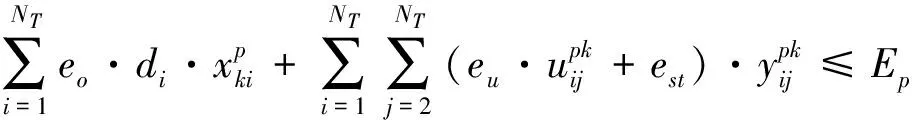
(11)

上述模型通过引入成像质量评价函数改进目标函数，同时考虑了任务间姿态转换、星上存储和能量等约束，是较为复杂的约束满足模型，本文采用离散差分进化与变邻域搜索相结合的算法进行求解。

3 DDE-VNS求解算法

敏捷卫星任务调度是NP-Hard问题[1]，具有组合优化特点，难于求解。相比于寻求最优解的精确算法，近似算法在求解卫星任务调度问题上取得了较好的效果，如遗传算法[2]、蚁群算法[5]。同时，遗传算法容易陷入局部最优，而蚁群算法依赖于控制参数和启发式信息。鉴于差分进化在全局搜索方面具有较好的性能，而变邻域搜索能提高算法的局部搜索能力，本文结合敏捷卫星任务调度问题特征，首先设计离散差分进化解的编码方式、初始种群生成方式、差分变异算子、交叉及辅助操作算子，然后采用变邻域搜索对离散差分进化每次迭代的最优解进行局部搜索，以寻找更好的邻域解，最后给出算法的实现流程。

3.1 离散差分进化设计

1)解的编码

对解进行编码是求解调度模型的首要问题。敏捷卫星的调度方案由每颗卫星的任务序列组成，本文根据任务执行顺序采用自然数编码方式，建立卫星与任务的对应关系，同时在不同卫星的任务序列间插入虚拟任务(用0表示)加以区分，形成DDE算法的个体编码。例如，x=[3 5 1 0 2 4 9 0 6 8 7]即为一个有效的个体编码。算法中个体的适应度值即模型中的目标函数值。

2)初始种群的生成

本文采用随机贪婪算法生成初始种群，具体步骤如下：

步骤1：通过预处理获得每颗卫星在可用轨道圈次上的候选任务，随机选择一个轨道圈次，计算该轨道圈次上候选任务的优先级之和Wsum、最早可观测时间的最小值Bmin和最早可观测时间的最大值Bmax。

步骤2：计算每个候选任务的选择概率ai，计算式如下：

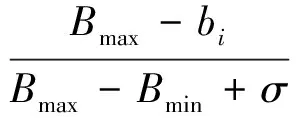
(12)

式中：σ是一个很小的正数。

步骤3：采用轮盘赌法选择一个任务，判断该任务是否属于禁忌表，如果不是，则判断是否满足约束条件，满足则写入任务序列，并更新禁忌表。

步骤4：判断是否有未选择的轨道圈次，如果有，则重复步骤1～3，如果没有，则搜索结束，将每颗卫星的轨道圈次按先后顺序排列，生成任务序列。

在初始种群的生成中，通过随机选择轨道圈次的方式减少了单颗卫星负载过大的情况，采用轮盘赌法选择候选任务增加了任务序列的多样性。

3)变异算子

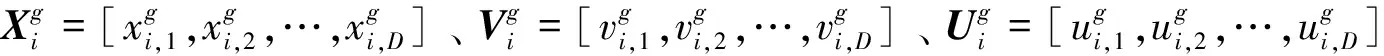
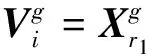
(13)

式中：r1、r2、r3为随机选择的三个个体，且r1≠r2≠r3≠i，F为缩放因子。应用于敏捷卫星任务调度问题，“⊕”和“⊗”运算通过下式计算得到

(14)

式中：rand(·)为(0,1)的随机数，mod(·)为取模运算，NT为任务数量。

通过上述操作得到变异个体不一定是合理的任务序列，但是考虑到变异的作用是对目标个体产生扰动，因此可以在交叉算子中设计辅助算子得到合理的任务序列。

4)交叉算子

根据DDE的机理[9]，试验个体由变异个体和目标个体通过交叉操作产生：

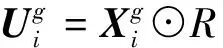
(15)

式中：R为交叉概率，⊙为辅助操作算子，针对敏捷卫星，本文设计了基于删除和插入邻域的辅助操作算子。交叉操作具体步骤如下：

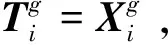
在基于删除和插入邻域的辅助操作算子中，每次寻找任务的可行插入位置时，需确定任务的观测时间，文献[1]采用基于最早可观测时间的方法，本文在此基础上，以接近时间窗口中心作为启发式规则确定观测时间。

经过交叉得到试验个体，一部分来自目标个体，另一部分来自变异个体，并且通过辅助算子(步骤2～3)确保了试验个体的合理性。

5)选择算子

采用一对一贪婪竞争机制选择适应度值较大的个体作为子代个体

(16)

3.2 变邻域搜索设计

在搜索过程中，充分利用问题信息增强离散差分进化的局部搜索能力是提高其优化性能的有效途径。鉴于目标种群的最优个体往往携带有价值的信息，因此对每次迭代的最优个体进行局部搜索，以获得更好的邻域解[7]。

为了减小邻域搜索的范围，提高搜索效率，本文结合敏捷卫星特点设计了三种邻域结构：插入邻域、替换邻域、移位邻域。插入邻域是将未选中执行的任务插入到卫星的任务序列中；替换邻域是指当插入邻域不满约束条件时，根据优先级关系替换任务序列中已安排的任务；移位邻域是指根据每颗卫星的负载，从负载最大的卫星任务序列中随机选择一个任务，将其插入到负载最小的卫星任务序列中。卫星的负载通过下式计算：

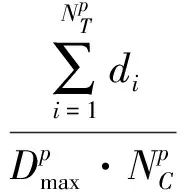
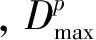
变邻域搜索的步骤如下：

步骤1：计算未安排观测的任务集，将其中任务按照优先级从大到小进行排列，选择优先级最大的任务，根据插入邻域计算可行的插入位置，如果能插入，将该任务写入禁忌表，如果不能，转向步骤2。

步骤2：若不能插入则选择使用替换邻域，如果不能替换已有序列中的任务，则将该任务写入禁忌表。

步骤3：采用移位邻域对多颗卫星的任务序列进行调整，产生新的邻域解。

步骤4：评价新解的适应度值，若大于当前最优解，则用新解替换当前最优解。

步骤5：判断当前是否满足终止条件，若满足最大迭代次数或最优解不变连续迭代次数，则结束搜索，否则转向步骤1。

3.3 算法实现流程

综合上述的分析和设计，DDE-VNS算法的实现主要包括三部分：算法初始化、DDE搜索、VNS搜索，其中算法初始化包括参数初始化和初始种群生成；DDE搜索即通过设计的变异、交叉和选择算子产生每一代的最优解；VNS搜索利用三种邻域结构对DDE每次迭代的最优解进行邻域搜索，获得新解并评价，然后更新最优解。DDE-VNS算法的实现流程如图1所示。

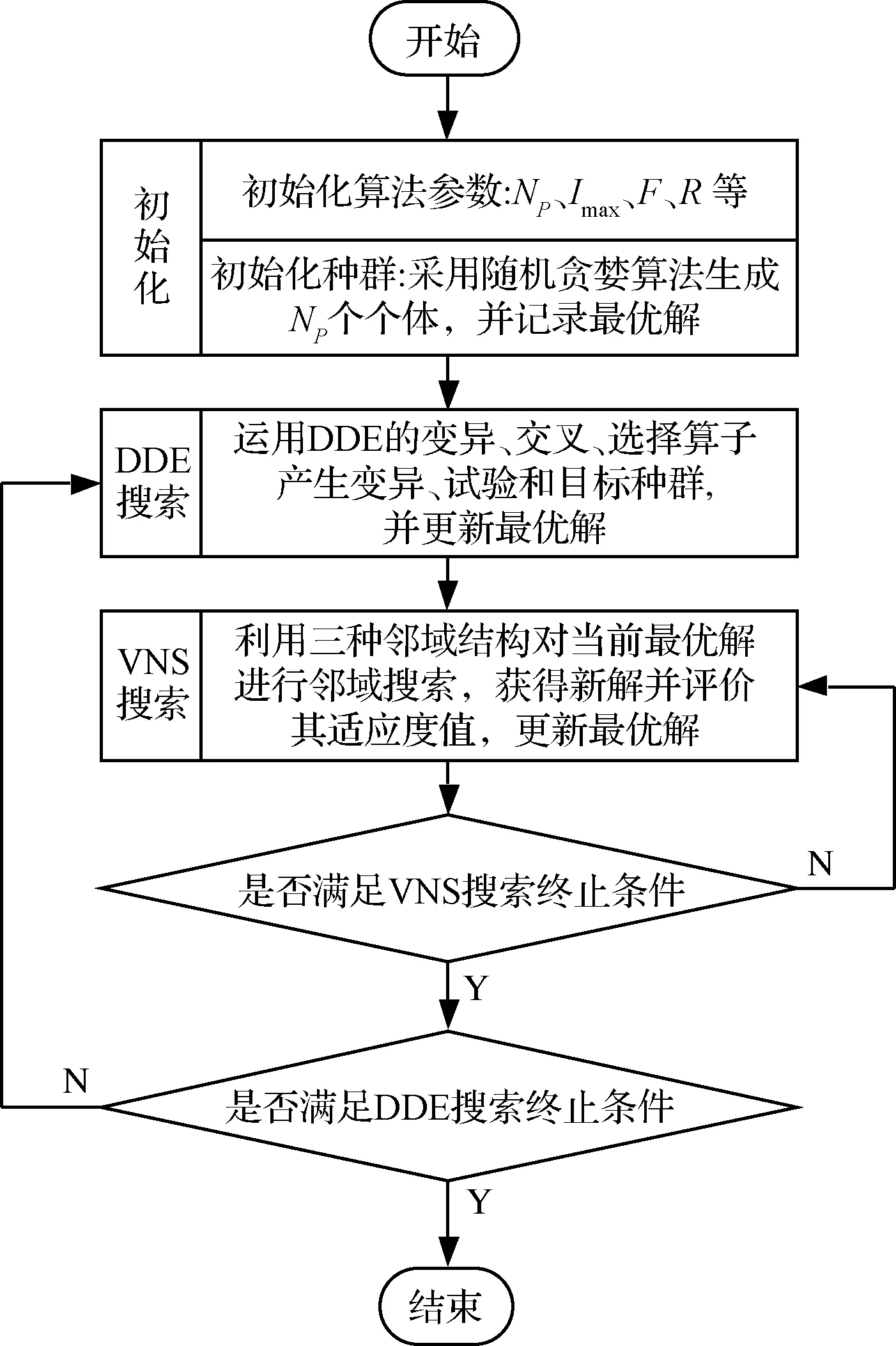
图1 DDE-VNS算法实现流程图Fig.1 Algorithm flowchart of DDE-VNS

4 仿真校验

采用Matlab R2010b对敏捷卫星任务调度约束满足模型的有效性和DDE-VNS算法的优越性进行仿真校验。

4.1 参数设置

仿真算例中敏捷卫星的轨道参数和有效载荷参数参考Pleiades卫星[1]，轨道高度为694km，轨道倾角为98.13°，升交点赤经为70.251°；成像任务采取随机生成的方式获得，考虑到点目标是成像的基本单元，而且条带目标可以看作具有一定观测时长的点目标，区域目标通过分解可由点目标和条带目标组成，本文选择在(60°E～150°E)、(0°N～50°N)的范围内随机生成5组不同规模的点目标任务集，分别为50、100、200、300、600个，每个任务的优先级为[1,10]之间的随机数。通过组合产生5组实例(卫星数-任务数)：2-50、3-100、4-200、5-300、6-600。

算法参数设置如下：离散差分进化中种群规模NP=100，进化代数Imax=300，缩放因子F=0.8，交叉概率R=0.5；变邻域搜索中最大迭代次数Gmax=10，最优解不变连续迭代次数Gremain=3。

4.2 调度约束满足模型仿真结果分析

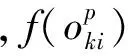
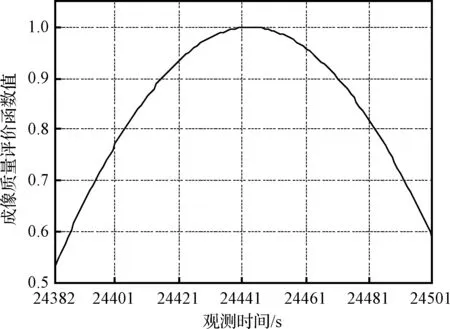
图2 成像质量随观测时间的变化Fig.2 Change of imaging quality with observation time

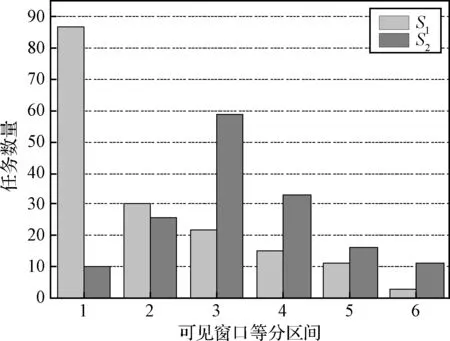
图3 两种方案的观测时间分布情况Fig.3 Distribution of observation time in different schemes

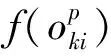
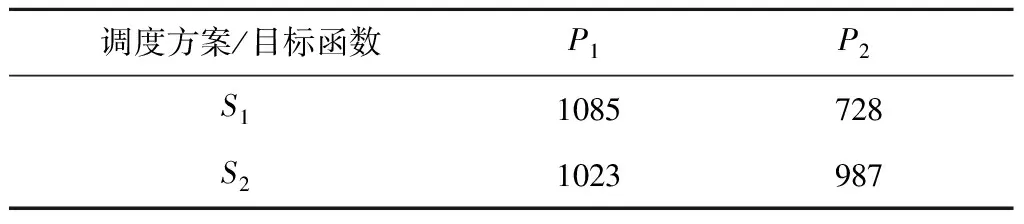
表2 不同目标函数下调度方案对比Table 2 Comparison of schedule schemes under different objective function

4.3 DDE-VNS求解算法仿真结果分析

为校验本文算法DDE-VNS的优越性，将本文算法与遗传算法(GA)[2]、蚁群优化算法(ACO)[5]、标准离散差分进化算法(DDE)[9]在5组算例上进行对比，目标函数采用综合考虑成像质量和任务优先级的P2，以平均收益、最大收益、最大任务数量、平均运行时间作为算法对比的主要评价指标。计算机配置为Intel Core i7-3770 CPU @3.4GHz、8核4GB内存，操作系统为Windows 7、编程环境为Matlab R2010b。每组算例运行20次并取平均值，结果如表3所示。

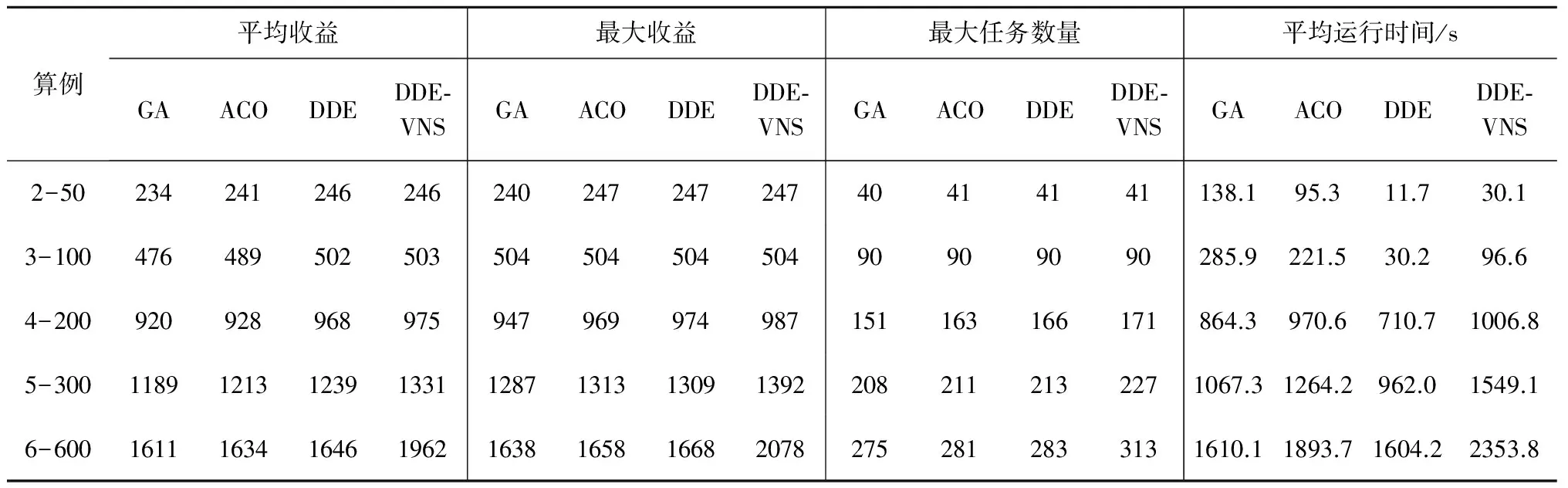
表3 本文算法与GA、ACO、DDE算法性能对比Table 3 Comparison of algorithm proposed in this paper with GA, ACO and DDE

由表3可知，与GA、ACO相比，本文算法在收益值和运行时间上均有优势，在收益值上分别平均提高了8.4%和6.7%，运行时间也较少，但随着算例规模的增大，其运行时间也大幅增加。与DDE相比，本文算法在收益值上平均提高了6.5%，同时，每次迭代中对最优解按照一定迭代次数寻找邻域解也增加了运行时间。此外，以算例4-200为例，将通过P2计算所得目标函数值作为收益值，GA、ACO、DDE、DDE-VNS的收敛性对比如图4所示。

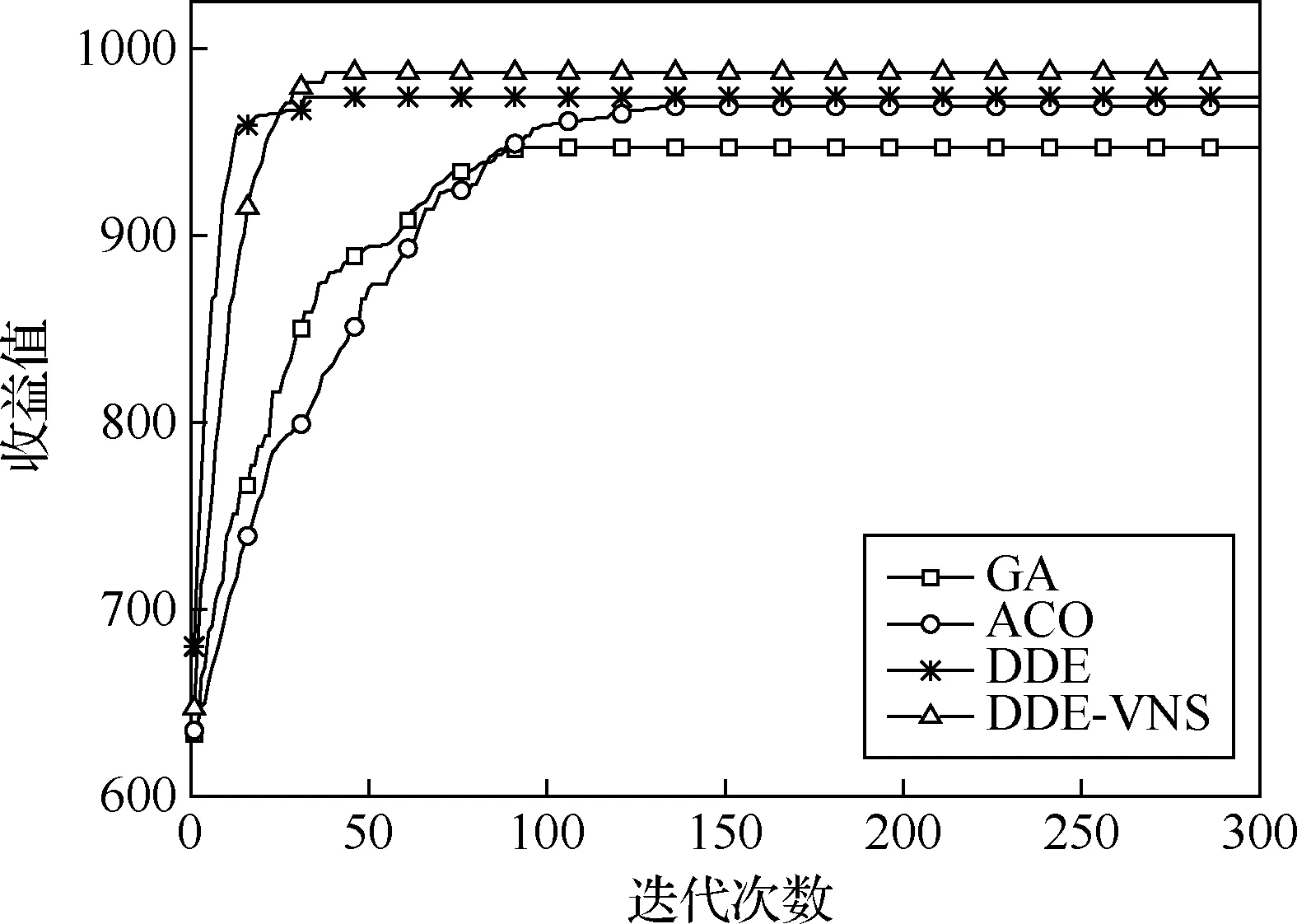
图4 算法的收敛性对比Fig.4 Comparison of convergence of different algorithms

由图4可知，本文算法在收益值和收敛速度上优于其他4种算法，GA和ACO，GA、ACO分别需要需运行93代、132代左右能够收敛到其最优解，而本文算法需35代左右即可收敛到最优解；本文算法与DDE在收敛速度上相差较小，分别为35代、32代左右，但本文算法在收益值上高于DDE。说明本文算法相对于GA、ACO具有更好的全局搜索能力，而VNS能够增强DDE的局部搜索能力，在全局探索和局部开发上较为均衡的DDE-VNS具有更好的性能。

5 结 论

本文描述了敏捷卫星任务调度时间约束，建立了考虑观测时间对成像质量影响、任务间姿态转换时间、星上存储与能量约束等因素的约束满足模型，设计了DDE-VNS求解算法，仿真结果表明，本文模型在调度方案的优化上更有效，DDE-VNS算法相对于其他算法在收益值和收敛性上更有优势，研究内容为敏捷卫星任务调度建模和求解提供了很好的途径。同时，本文研究没有考虑调度中不确定因素的影响，如应急任务加入、卫星资源失效、云层遮挡等。在后续工作中，可进一步考虑这些不确定因素，研究不确定条件下的调度模型与求解算法，以期促进敏捷卫星任务调度方法的不断完善。

[1] Lemaitre M, Verfaillie G, Jouhaud F, et al. Selecting and scheduling observations of agile satellites[J]. Aerospace Science & Technology, 2002,6(5):367-381.

[2] Li Y, Xu M, Wang R. Scheduling observations of agile satellites with combined genetic algorithm[C]. The Third International Conference on Natural Computation, Haikou, China, Aug. 24-27,2007.

[3] Tangpattanakul P, Jozefowiez N, Lopez P. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite[J]. European Journal of Operational Research, 2015, 245(2): 542-554.

[4] Bunkheila F, Ortore E, Circi C. A new algorithm for agile satellite-based acquisition operations[J]. Acta Astronautica, 2016, 123: 121-128.

[5] Xu R, Chen H, Liang X, et al. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization[J]. Expert Systems with Applications, 2016, 51: 195-206.

[6] Wang X, Chen Z, Han C. Scheduling for single agile satellite, redundant targets problem using complex networks theory [J]. Chaos, Solutions and Fractals, 2016, 83: 125-132.

[7] 王凌,钱斌.混合差分进化与调度算法[M].北京: 清华大学出版社, 2012:204-222.

[8] Storn R, Price K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization, 1997, 1(4): 341-359.

[9] Pan Q K, Wang L, Gao L. An effective hybrid discrete differential evolution algorithm for the flow shop scheduling with intermediate buffers[J]. Information Sciences, 2011,181(3):668-685.

[10] 薛羽, 庄毅, 顾晶晶, 等. 自适应离散差分进化算法策略的选择[J]. 软件学报, 2014, 25(5): 984-996. [Xue Yu, Zhuang Yi, Gu Jing-jing, et al. Strategy selecting problem of self-adaptive discrete differential evolution algorithm[J]. Journal of Software, 2014, 25(5): 984-996.]

[11] 张春美,陈杰,辛斌. 武器目标分配问题的离散差分进化算法[J]. 北京理工大学学报, 2014,34(3):289-293. [Zhang Chun-mei, Chen Jie, Xin Bin. A discrete differential evolution algorithm for the weapon target assignment problem[J]. Transactions of Beijing Institute of Technology, 2014,34(3): 289-293.]

[12] 皮本杰, 翟淑宝. 信号采集系统星地资源快速调度优化方法[J]. 宇航学报, 2016,37(3):348-356. [Pi Ben-jie, Zhai Shu-bao. Quick optimal schedule method of onboard and ground resources for signal collection satellite system[J]. Journal of Astronautics, 2016,37(3): 348-356.]

[13] 陈锦伟. 敏捷卫星遥感图像配准和拼接技术研究[D]. 杭州: 浙江大学, 2014. [Chen Jin-wei. Research on registration and stitching of remote sensing image of agile satellite[D]. Hangzhou: Zhejiang University, 2014.]

[14] Rosa B, Souza M, Souza S, et al. Algorithms for job scheduling problems with distinct time windows and general earliness/tardiness penalties[J]. Computers and Operations Research, 2017, 81: 203-215.

通信地址：北京市怀柔区八一路1号(101416)

电话：13522097833

E-mail:lemonslee@163.com

Task Scheduling Model and Algorithm for Agile Satellite Considering Imaging Quality

LI Zhi-liang1, LI Xiao-jiang2, SUN Wei3

(1. School of Postgraduate, Academy of Equipment, Beijing 101416, China;2. Department of Space Equipment, Academy of Equipment, Beijing 101416, China;3. School of Instrumentation Science and Opto-electronics Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China)

A constraint satisfaction model and a discrete differential evolution combined with variable neighborhood search (DDE-VNS) are proposed in this paper for an agile satellite task scheduling considering the influence of the observation time on the imaging quality. Firstly, the temporal constraint of the agile satellite task scheduling is described. Secondly, considering the influence of the observation time on the imaging quality, the constraint of the attitude transition between tasks, and onboard storage and energy, the constraint satisfaction model of the agile satellite task scheduling is established. Thirdly, the mutation, crossover and selection operators of the discrete differential evolution are designed, the variable neighborhood search is adopted to exploit better solution from the optimal solution at each iteration, and also the workflow of the proposed algorithm is described. Simulations have demonstrated that the model and algorithm proposed can get schedule plans with cracking reward and quick converge.

Agile satellite; Task scheduling; Discrete differential evolution; Variable neighborhood search

2016-11-21;

2017-04-25

V19

A

1000-1328(2017)06-0590-08

10.3873/j.issn.1000-1328.2017.06.005

李志亮(1988-)，男，博士生，主要从事航天任务分析与设计研究。