平行四边形面积教学以数学臆测活动引发小学生论证初探

邓莹源

摘 要：数学臆测是一种从提出猜想到证明猜想的循环历程，从数学学习的观点来讲，数学臆测活动不仅是启动学生主动思考的引擎，它还能启动数学探究和引燃數学论证。数学臆测之后便是提出猜想。但是猜想不一定都是有效的，为了检验猜想是否有效，数学论证由此产生，所以数学臆测是伴随着论证发生的，两者关系极为密切。笔者以“平行四边形面积”一课为例，以臆测活动进行教学，实践证明引发小学生进行论证，经历主动学习的可行性。

关键词：平行四边形面积；教学；数学臆测；论证

一、背景和研究价值

“平行四边形面积”是最基本的图形面积计算之一，在几何学中有着广泛的应用。“平行四边形面积”是小学生学习三角形面积、梯形面积和其他组合图形面积的重要基础，在三角形面积和梯形面积的推导过程中具有非常重要的作用和价值。同时“平行四边形面积”也是小学数学学习中重要的传统教学内容之一。但是我们发现，在实际的教学中，学生的学习存在一些困惑：

1. 平行四边形的面积为什么一定是“底×高”呢？

2. 既然在进行公式推导的过程中是将平行四边形转化为长方形进行推导的，那么，平行四边形的底与长方形的长是相等的，但平行四边形的高与长方形的宽是否相等？为什么不相等呢？

而如果教师在课堂教学中能引导学生先对平行四边形的面积进行猜想，继而鼓励学生自己去验证猜想，得出正例或反例，再引导学生再次猜想、验证，最终形成结论，这样就能很好地解决学生的困惑。而这个过程，我们认为它就是一个很好的以数学臆测活动引发学生论证主动学习的过程。

从数学学习的观点来讲，数学臆测活动不仅是启动学生主动思考的引擎，它也能启动数学探究和引燃数学论证。数学臆测之后便是提出猜想，但是猜想不一定都是有效的，为了检验猜想是否有效，数学论证随之产生，所以数学臆测是伴随着论证发生的，两者关系极为密切。依据Stylianides（2007）提出证明是一种论证，论证包含三个元素：一组叙述、论证方法（如演绎法、数学归纳法、举反例等）、论证方法的表征。以此观之，数学论证需要涉及较高层次的解题历程，故并非任何一堂数学课学生的论证都会发生，若教师能在课堂制造机会让学生进行数学臆测活动，则学生的论证历程较有可能发生，也就是说，数学臆测可以引发数学论证，数学臆测是启动数学论证的动力。

数学论证固然重要，但这样的习惯与能力学生需要在何种场域培养呢？依据陈英娥与林福来对数学论证的研究发现建议：若要培养学生的论证能力，则需要把说理变成是一种习惯。数学论证会展现在教师与学生互动的数学沟通活动中。

本研究旨在通过“平行四边面积教学”这一案例，研究以数学臆测活动来引发学生经历数学论证的可行性。

二、核心概念界定：数学臆测活动论证

（一）数学臆测活动

数学臆测是一种从提出猜想到证明猜想的循环历程，而每个个体面对相同的任务进行的臆测历程会有所不同，即使相同的个体面对不同的任务所进行的臆测历程也会有所不同。有关形成臆测的历程，Caadas等提出五种类型：从有限例归纳、从动态例归纳；、模拟、溯因推理和知觉为基础的臆测。Caadas与Castro（2005）又将每一种类型细分成数个阶段，例如以学生最常使用的从有限例归纳进行臆测的臆测类型为例，需要经历七个阶段：（1）观察有限例；（2）组织有限例；（3）寻找规律或样式；（4）形成猜想；（5）检验猜想；（6）将猜想一般化；（7）证明猜想的一般化。也就是说，个体在面对任务时，第（1）阶段需要从给定的一个或两个有限例子开始进行观察；第（2）阶段用系统的列举法或使用表格将这些例子组织起来；第（3）阶段从组织的资料中寻找规律性，使所发现的规律也适用于其他没有列出来的例子中；第（4）阶段是形成猜想，是依据所发现的规律提出猜想，使得此猜想能适用于所有可能的例子中，但也仍然在存疑或不确定的状态中；第（5）阶段是检验猜想，再检验更多不同的例子或不同的方法，看看此猜想是否正确，但此时所提出的猜想还未推广到一般化；第（6）阶段是将所提出的猜想推广到一般化，这个阶段的猜想要排除存疑或不确定的情况，使猜想成为可接受的数学性质；第（7）阶段是要证明猜想的一般化，这个阶段要用合理的数学知识来解释或证明此猜想，以取信他人。

由于本研究的目的是要通过数学臆测来引发学生的数学论证，所以Caadas与Castro所提出的从有限例归纳进行臆测的臆测类型及臆测历程，将作为本研究用来协助教师设计臆测任务的基本要素，将数学臆测融入于数学课堂教学中，以发展学生的数学论证。并非所有的数学任务都能导向数学臆测，由于本文数学臆测任务的使用对象是三年级学生，他们是第一次接触数学臆测教学活动，而且他们的数学知识体发展还不够丰富，因此教师在设计该任务时，并不考虑纳入最后两个阶段：将猜想一般化及证明猜想的一般化。

（二）论证

依伟氏字典定义，论证是一些逻辑相关的论述。Toulmin（1958）将论证解释为从已知数据推演到结论的过程中用来支持结论的证据，这些证据可能是一些推理规则或数学原理或定理，但不一定是演绎的。有些学者将数学论证分为两个层面：论证的过程及论证的成果。论证的过程是产生一个逻辑相关的对话过程，而论证的成果是讨论过程所产生的论述。说出或写下的叙述，可能是归纳，也可能是演绎、模拟、溯因（abduction）或其他推理。虽然对于数学论证的定义，各学者之间有不同的说法，但仍有其共通点：论证是支持或反对一个命题或意见的理由，它可以是语言文字、数字数据或图画的形式。数学论证活动涉及证明与反驳的过程，对发展学生的数学思维具有重要意义。本研究所界定的数学论证是在课堂中进行数学臆测教学活动脉络下产生的，故它是数学臆测的一部分，数学论证在本研究中被定义为从建立数据、建立证据到作为形成论述或检验论述的证据或依据，以支持结论的过程。

数学教育的研究经常将论证和证明连接在一起，Douek（1999）将证明视为论证的一种。Krummheuer（2007）认为证明通常是属于个人的数学活动，但数学论证是一种社会化的过程，所以论证不被视为是用来促成或阻碍证明的学习，而是被视为数学学习的本质。有关论证活动的发展，Douek和同事将其分为六个阶段：进行猜测，形成叙述，效化猜想，将前后连贯具有理论性的论述串成一个演绎炼，将这些论述炼组织成一个可接受的证明，最后是朝向形式化的证明。

依据Boero等提出论证活动发展的阶段，论证的产生也始于臆测活动，似乎也将论证视为社会化的过程，是数学活动的一部分，包含形式化的证明。基于此，本研究将数学论证视为一种社会化过程，若要发展学生的数学论证，则需要教师在课堂中制造让学生和教师互动的机会，而且借由课堂中的论证分析来了解学生的论证历程，协助教师进行证明或推理的教学。

三、理论基础

（一）数学臆测理论

数学臆测是个体面对不确定的数学问题时，依据已知条件或知识，进行猜测、检验、相信和反驳的过程（林福来、陈英娥）。数学臆测在本研究中的意义体现在数学课堂中，建立资料是由个别或小组学生自己来完成，紧接着是由个体观察资料寻求规律性，并提出猜想，再借由小组或全班共同检验猜想的正确性，以及以不同的例子验证猜想的合理性的巡回历程。

数学臆测是一种从提出猜想到证明猜想的循环历程，而每个个体面对相同的任务进行的臆测历程会有所不同，即使相同的个体面对不同的任务所进行的臆测历程也会有所不同。现有五种臆测历程：从有限例归纳、从动态例归纳、类比、溯因推理和知觉为基础的臆测。由于本研究的目的是要通过数学臆测来引发学生的心智活动，帮助学生轻松愉快地自主发现并理解公式，改变学生的思考方式。所以从有限归纳进行臆测的臆测类型及臆测历程，将作为本研究用来协助教师设计并教学的基本要素。

本研究中的数学臆测活动任务设计的理论基础也是依据的林福来教授的数学臆测活动的四个设计原则。原则一：教师要提供机会让学生进行目标导向的观察以促成数学臆测，“观察”设计原则是教师要提供机会让学生有目的或系统地观察有限例，以帮助学生能将发现的数学关系推广到一般化。原则二：教师要提供机会让学生进行有意义的建构以促成数学臆测，“建构”设计原则是教师需要鼓励学生依据能通往臆测的先备知识建构新知识。原则三：教师要提供机会让学生进行先备知识的转换以促成数学臆测，“转换”设计原则是教师需要提供机会让学生进行算法或公式的转换，以产生数学臆测。原则四：教师要提供机会让学生进行反思以促成数学臆测。由于学生在转换的过程中可能导致不正确或无意义的叙述或猜想，因此“反思”的设计原则是必要的。

（二）林福来提出的小学生数学论证理论

五种推理方式以及演绎推理法是数学论证学习过程贡献于学生发展思考方法的主要内涵，这五种推理方式为：

1. 根据有限例子归纳推理。

2. 观察动态例子，归纳其不变性。

3. 类比推理：根据对物件间对应结构的相似性的感知与建构进行推理。

4. 溯因推理：观察到结论性的现象，追溯成因。

5. 图像推理：根据具体图像，或直观性或直觉性来推论。

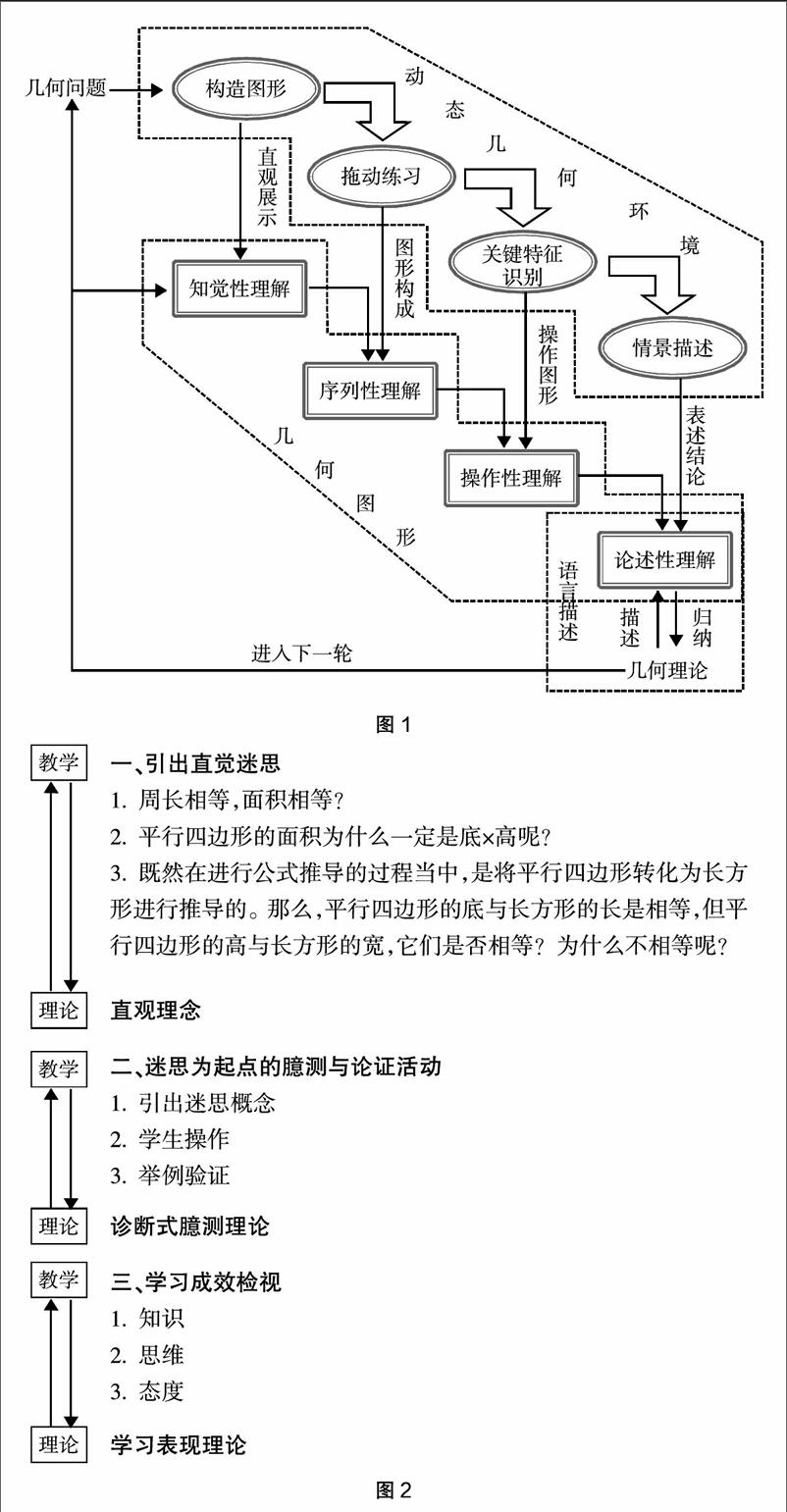
（三）Duval提出的几何学习四种理解：直觉性理解、序列性理解、操作性理解和论述性理解

Duval理论与范希礼理论的区别在于，范希礼的几何思维水平研究的重点在于建构几何系统的逻辑顺序，而Duval理论侧重于结合问题的理解过程，特别是如何由几何图形的呈现到几何推理与证明，为几何问题的解决提供了理论依据。

四、研究的主要内容及研究框架

（一）研究的主要内容

1. 对平行四边形的面积进行教材分析，提出教材中可融入臆测活动来实现学生自主学习建构知识模型的臆测任务。

2. 根据Caadas与Castro（2005）的臆测七个阶段来设计出具有数学臆测本质的任务。

3. 通过课堂教学实践，检测、总结、归纳以数学臆测活动引发小学生论证的可行性。

（二）研究框架

框架如图2所示。

五、研究结果与启示

（一）研究结果

在该任务的臆测活动中，五年级学生经历了五个臆测历程：造例子及组织例子、观察例子并寻求规律性、形成并提出猜想、验证猜想。实践教师设计的数学臆测任务尝试提供给学生的臆测历程的每个阶段都是先由个别学生，再到小组，最后到全班的检验。因为每个环节的检验都需要学生说服他人，论证由此产生，因而有个人的论证、小组的论证和全班的论证。我们发现，通过数学臆测活动引发学生论证具有5个特质：

1. 通过臆测活动产生的每个论证（数学性质）是经过个人、小组，再到全班三个层级不断论辩，经过初始的猜想到最后得到稳定的数学性质。

2. 人数越少论证结构越简单。因为小组人数只有4人，小组内的论证结构較为简单，而因全班学生加上老师共51人，所以全班的论证人数较多，论证历程较长也较为复杂。虽然越长或越复杂的论证并不见得品质越好，但师生互动却比较多。

3. 该任务下有关平行四边的面积不是相邻边相乘而是底乘高的论证历程，该五年级实验班的学生第一次接受数学臆测活动，所展现的臆测都集中在Caadas与Castro所提出的从有限个例子归纳进行臆测的臆测类型。

4. 该五年级实验班学生展现了Caadas与Castro七个阶段的臆测认知历程的前5个阶段，但是没有展现出后面的两个阶段：将猜想推广到一般化及证明猜想一般化。其理由为：五年级学生第一次体验臆测融入教学，且他们的数学知识还不够丰富。我们在今后的教学中会继续进行将猜想推广到一般化及证明猜想一般化的活动。

5. 通过数学臆测活动引发学生论证，在论证过程中能促进学生数学学习。通过实验，我们认为数学臆测活动能融入数学课堂教学中，学生能展现出数学论证的样貌，也能在课堂上积极参与；我们认为数学臆测确实能点燃学生的数学论证，也让学生的数学学习真正地发生了。但目前仅通过这一节课，我们暂时也无法回答有关数学臆测任务对学生论证品质有多大影响的问题。

（二）研究启示

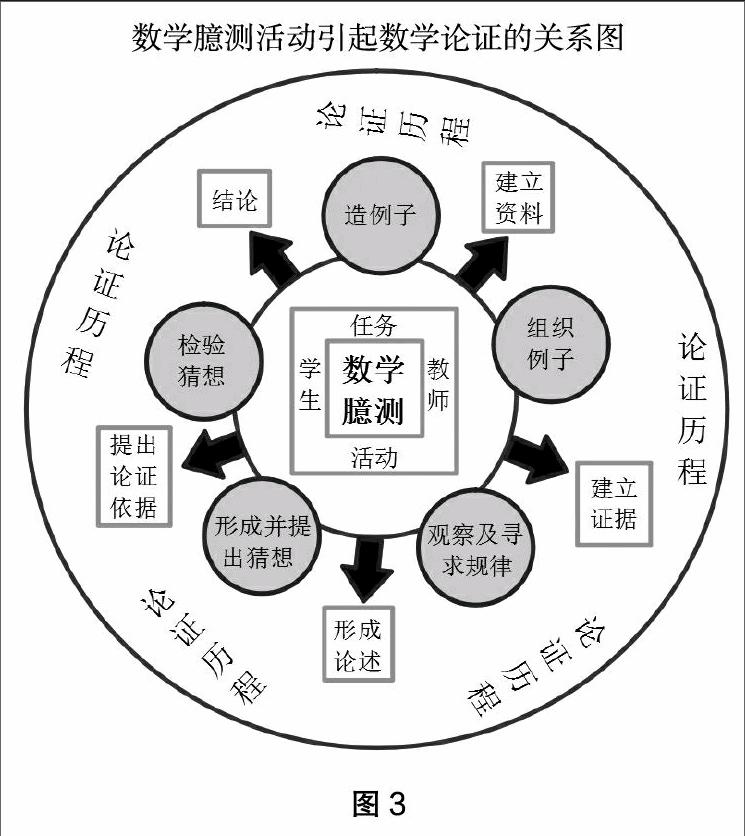
本研究发现，学生的数学论证确实在实验教师进行数学臆测任务的数学课堂中发生了。数学臆测引发学生数学论证，两者的关系图如图3所示：

图3包含了两个圆和一个长方形，长方形在圆形的最里面，外面紧接一个内圆和一个外圆。圆形表示数学臆测元素和数学论证元素，长方形表示促进数学臆测活动进行的关键性角色。最里面的长方形表示在数学课堂内促进臆测活动引发数学论证发生的重要的关键性角色，包含任务本身、数学臆测活动内容、学生的数学已有知识及教师的介入。内圆阴影是数学臆测历程的5个历程：造例子、组织例子、观察和寻找规律性、形成并提出猜想、检验猜想。箭头向外，象征着数学臆测活动启动了在外圆的数学论证。数学论证的基本元素包含建立资料、建立证据、提出或形成论述、提出论证依据及结论，它们分别以方形表示。数学臆测活动的前两个历程：造例子和组织例子，是为了建立资料，作为提出论述的准备。臆测活动的第三、第四个历程：观察寻求规律及提出猜想，是为了形成论证活动中似真但还不确定的论述。臆测活动的第五个历程是启动个别学生或小组或全班需要提出论证依据来捍卫自己所提出的论述，其他学生也可能举出例子来反驳似真的论述，最后经过全班学生共同检验论述，得到一个或多个结论。