融资约束下CPPI策略风险分析

丁钊鹏，刘立新

（1.对外经贸大学金融学院，北京100029；2.北京联合大学，北京100101）

融资约束下CPPI策略风险分析

丁钊鹏1,2，刘立新1

（1.对外经贸大学金融学院，北京100029；2.北京联合大学，北京100101）

在融资约束之下，通过定义三种资产状态，文章计算出投资组合价值在三者之间的转移概率矩阵，并推演出各概率值与风险乘数、资产波动率、期望收益率、无风险收益率和投资者风险偏好诸要素之间的增减关系。以沪深300指数作为风险资产，在四类典型波动的市场，推算出融资约束下不同调整周期与风险乘数对应的期末组合价值以及各状态的期初期末转移概率，并阐述了市场状况与投资组合保险策略的选择关系以及风险头寸与组合保险失败的联系。

投资组合保险；风险乘数；融资约束；转移概率

0 引言

投资组合保险策略，即投资机构在保障资金安全的前提下，在各资产类别之间动态线性配置投资资金比重，以期获得较高的市场收益率。

对于投资组合策略，一个基本的前提假设是：可用资金量不存在任何限制。但在CPPI策略中，倘若风险乘数过大，随着市场的变化，一定时期，风险资产投资额度理论上可能会高于当期投资组合价值总额，因此，当期资产不但悉数应投向风险资产，尚且需要借助外部融资杠杆投向风险资产。然而对于很多基金来说，融资约束通常存在，甚至不允许外部杠杆借贷，况且，即使不存在融资约束，过高的杠杆融资成本也将使多数投资者望而却步。本文拟在融资约束之下，通过定义三种资产状态，利用转移概率矩阵，推演出各概率值与风险乘数、资产波动率、期望收益率、无风险收益率和投资者风险偏好诸要素之间的增减关系，在融资约束下，以沪深2011—2014年四个有代表性的风险市场推算出不同调整周期与风险乘数所对应的期末组合价值以及各状态的期初期末转移概率，并阐述了市场状况、风险头寸与组合保险策略选择之间的内在关联。

1 融资约束下的条件转移概率

策略的基本理论公式和符号：

Vt:t时刻投资组合价值；

Ct:t时刻缓冲值；

Ft:t时刻要保额度；

Et:t时刻风险资产投资价值；

St:t时刻风险资产市场价格；

Dt:t时刻无风险资产市场价格；

G:投资者要求的期末要保额度价值；

m:风险乘数；

r:即期无风险收益率。

按照CPPI策略，投资者根据风险偏好在期初设定风险乘数m以及t时刻所需要保额度Ft，风险资产投资额度为风险乘数乘以缓冲值Ct=Vt-Ft，余下份额投向无风险资产。随着市场上风险资产价格的变动以及投资保险期限逐步收缩，风险资产与无风险资产二者之间的投资权重需要投资者动态调配。此处的风险乘数（m＞1）对应于投资者的金融杠杆，越高的风险乘数，代表投资者越风险偏好，投资者在风险资产升值中具有更诱人的杠杆收益；反之，一旦风险资产下跌，则投资组合价值损失成倍放大，在来不及重配资产并止损的情况下，投资组合将无从保险。

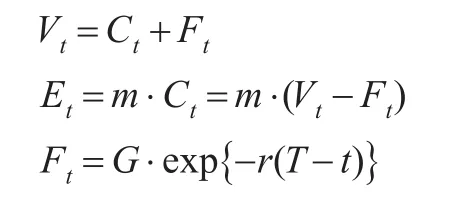
定理1：按照Black-Scholes的假设，且无风险资产收益率、风险资产漂移率及波动率和都是固定值，可得投资组合价值将满足：

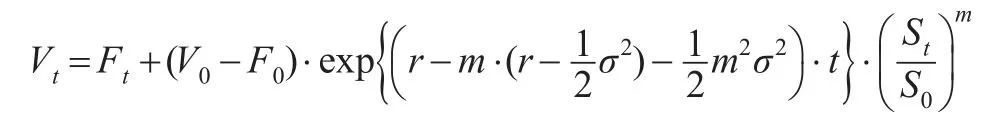
倘若存在融资约束，即投资者投资于风险资产的头寸受到外部融资的限制，那么风险资产头寸将定义为：

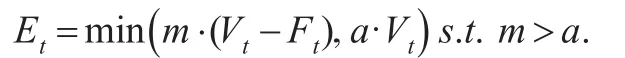
其中，a表示当期组合价值用于风险资产头寸的上限比率，它刻画了投资者的风险偏好程度。则可以得到，在任意投资组合调整周期Δt=ti-ti-1内，总是存在三种不同的投资组合价值状态：

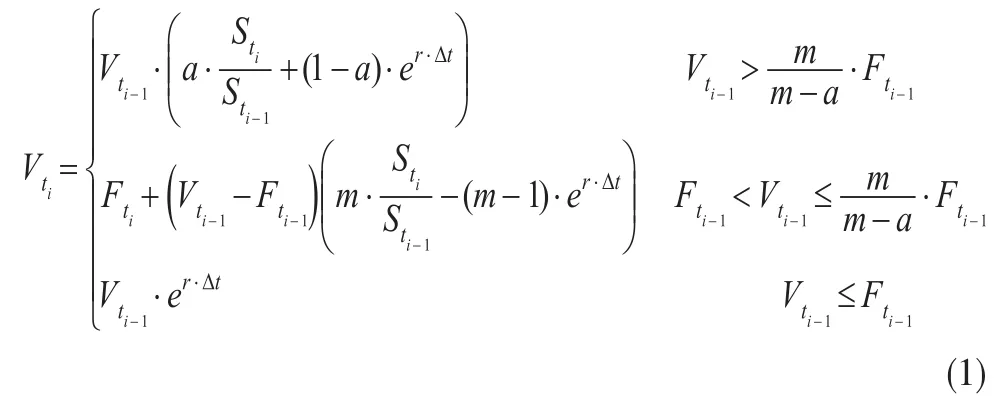
定理2：从ti-1至ti这段时间区间，投资组合价值三种状态之间存在一定的转移概率，且令条件转移概率矩阵为：

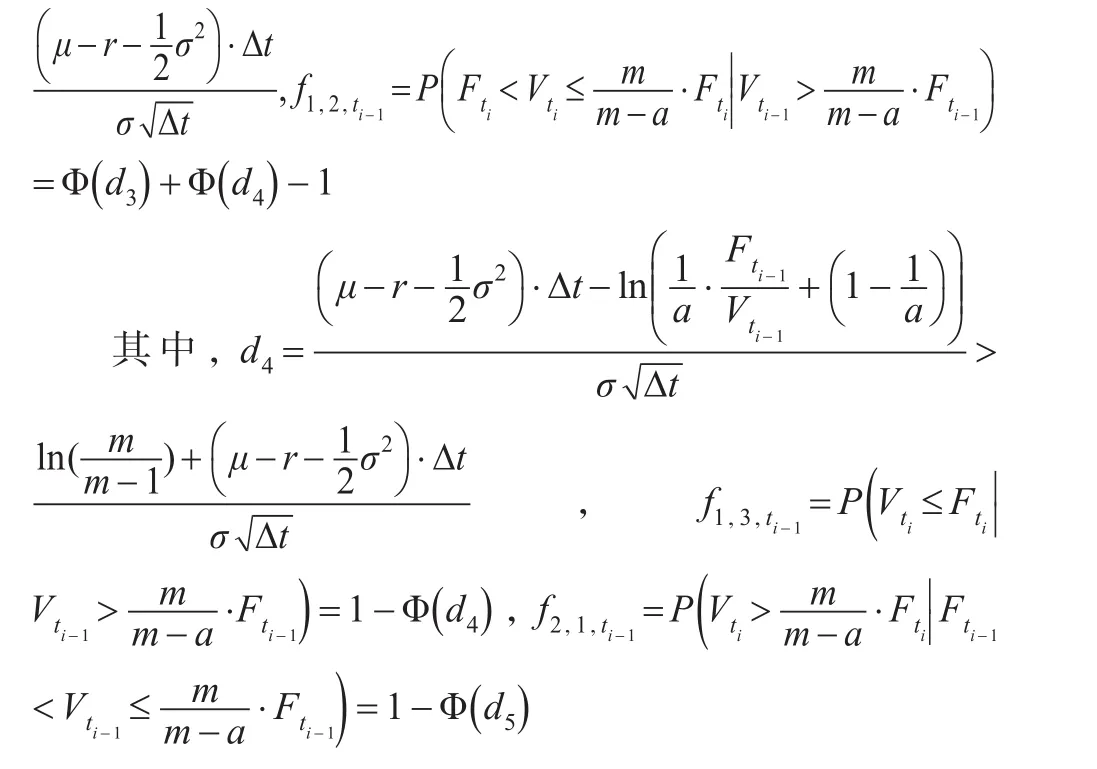
其中：

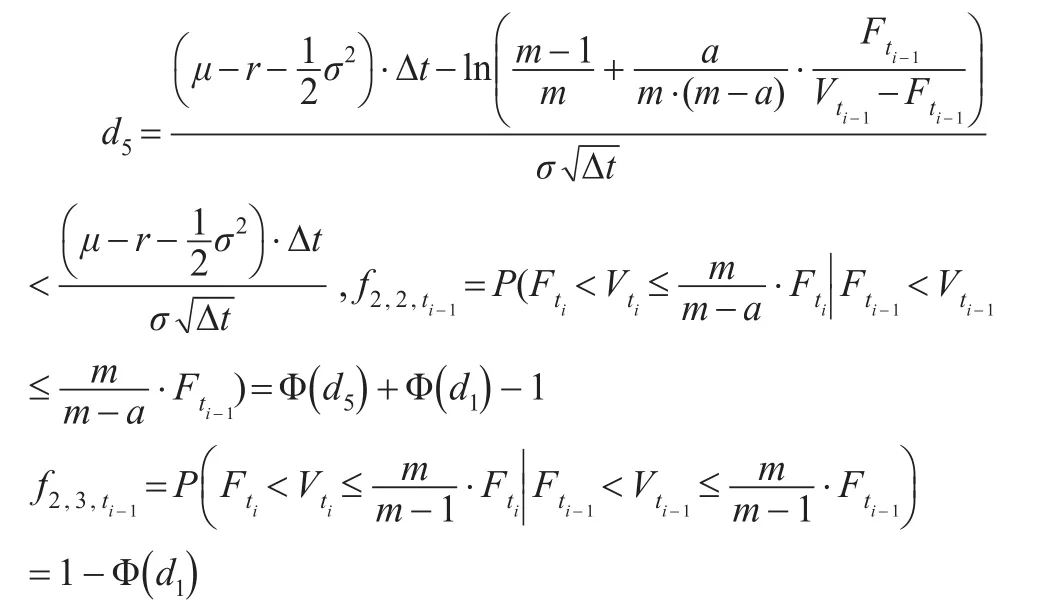
推论1：条件转移概率矩阵：

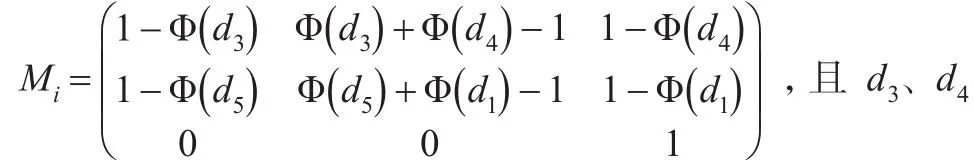
d5皆依赖于该时间区间内期初要保额度与投资组合价值

且由上面分析可知：d4＞d1＞d3＞d5，因此

上面的不等式表明：当前一期投资组合价值超过要保额度时，下一期超过投资上限限额（转移至状态1）的概率必将大于不能保底的概率（转移至状态3），亦即，无论取什么样的参数，当期保险失败的条件概率永远不可能超过50%。

由d1、d3、d4、d5各自的定义，将之关于m、σ、μ、诸因素进行相应的敏感度分析，可以得到相互之间的增减关系如表1所示：

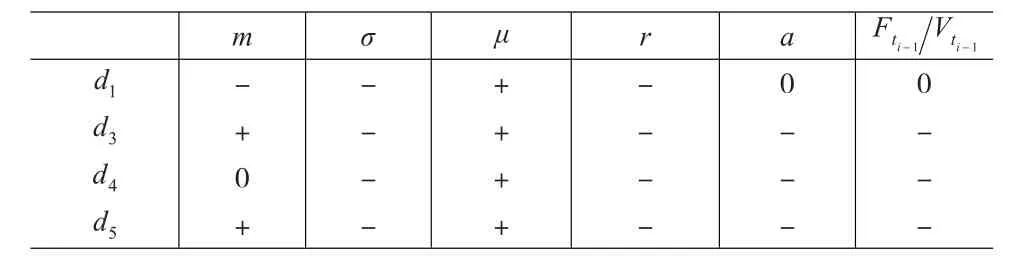
表1 各因素对d1、d3、d4、d5的影响

结合条件转移概率的定义，可以得到各概率值与相应要素之间的关系如下页表2所示。

表2 各因素对转移概率的影响

推论2：从表2可以看出：随着风险乘数m的增大，状态1与状态2能够保持或上升到状态1的概率减少，虽然状态1跌至状态3的概率未变，但是状态2跌至状态3的概率却上升了，因此，风险乘数若增加，缺口风险将会上升。

随着风险资产波动率σ的增大，状态1与状态2保持之前状态的概率均减少，但是转移至状态1与状态3的概率均有所增加，因此波动率使得未来的走向变得更加的不确定：或者更好，或者更坏。这并非单由波动率可以决定，总体上说，波动率若增加，缺口风险会上升。

随着风险资产漂移率μ的增加，与波动率σ的作用恰好相反，它会使得投资组合价值向状态2集中，转移向状态1与状态3的概率皆会缩小，从而价值状态越趋稳定，漂移率若增加，缺口风险会减少。

随着无风险资产收益率r的增加，与风险资产漂移率μ的作用恰好相反，它会使得投资组合价值以更大的概率向状态1与状态3转移，而状态2的概率减少。原因在于，无风险收益率是要保额度的增长率，也是风险资产的机会成本，所以无风险收益率若增加，缺口风险会增加。

随着融资约束比率a的增加（限制减弱），则向上的收益空间更大，亦即向状态1转移的概率增大，从而降低了投资组合价值在状态2中的概率，但是由于杠杆交易的作用同时也放大了从状态1陡然下降到状态3的概率，因此，融资约束比率若增加，缺口风险会上升。

a，故效果与之相似，投资更激进，缺口风险也会更大。

推论3：令ti时刻的非条件状态概率分别如下：

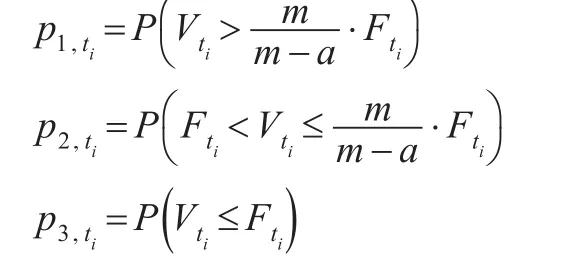
由上面的分析可知，该状态概率是路径依赖的

2 融资约束下CPPI策略实证分析

风险资产采用沪深300指数，图1为该指数2011—2014年的走势。

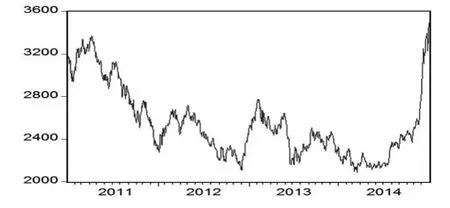
图1 沪深300质素2011—2014年走势图

2011 年，沪深市场处于跌势，日最大跌幅达到3.87%；2012年，沪深市场震荡中收涨，日最大跌幅达到2.88%；2013年，沪深市场震荡中收跌，日最大跌幅达到6.52%；2014年，沪深市场处于涨势，日最大跌幅达到4.59%。选取这四年作为实证的原因，即在于这四年的沪深市场囊括了具有代表性的四类风险资产波动类别。以一年作为组合投资期限，进行不同市场的比较实证，无风险收益率则参考一年期国债收益率。

期初，假定组合价值为100，并以期初组合价值的90%作为期末的要保额度，亦即G=90。沪深股票交易是按成交金额的千分之三收取佣金，并按成交金额的千分之一收取印花税，实证中假定风险资产换手金额的千分之四作为总交易费。

在不可融资限制下（a=1），以0.025为间隔选择风险乘数m∈(1，10]，选择组合调整周期△t=1，5，10，20，30，40（分别对应日、周、两周、四周、六周、八周），可以得到2160种组合。

可以计算出不可融资限制下不同调整周期与风险乘数对应的期末组合价值，如图2所示：

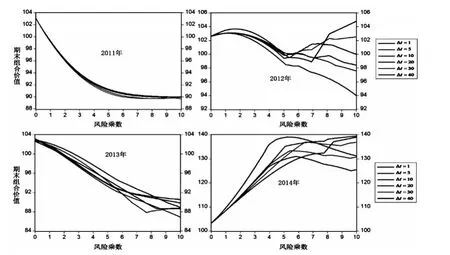
图2 不可融资条件下期末组合价值

从最低期末组合价值比较可见，在市场下跌或震荡收跌之时，不可融资的限制并未保证投资组合保险的成功。

根据图2，可以得到不可融资限制下最优的风险乘数和调整周期，如表3所示：

表3 不可融资限制下最优的固定风险乘数和调整周期

若存在外部融资约束，在下跌或震荡收跌的市场，最好避免投资风险资产；而对于上涨或震荡收涨的市场，最优策略却是选择较高的风险乘数和较长的调整周期。较高的风险乘数可以通过较大的权重投资于风险资产从而获得较多的风险收益率，而较长的调整周期则可以最大程度上避免因频繁换手对应的波动回调和交易费用对于收益的吞噬。

同时，在不可融资限制下，以0.025为间隔选择风险乘数m∈(1，10]，选择△t=1，5，10，20，30，40，可以得到2160种组合，按之前的定义，组合价值的三种状态依次为：状态1、状态2、状态3，从而计算得到各状态的初始概率与转移概率如表4所示：

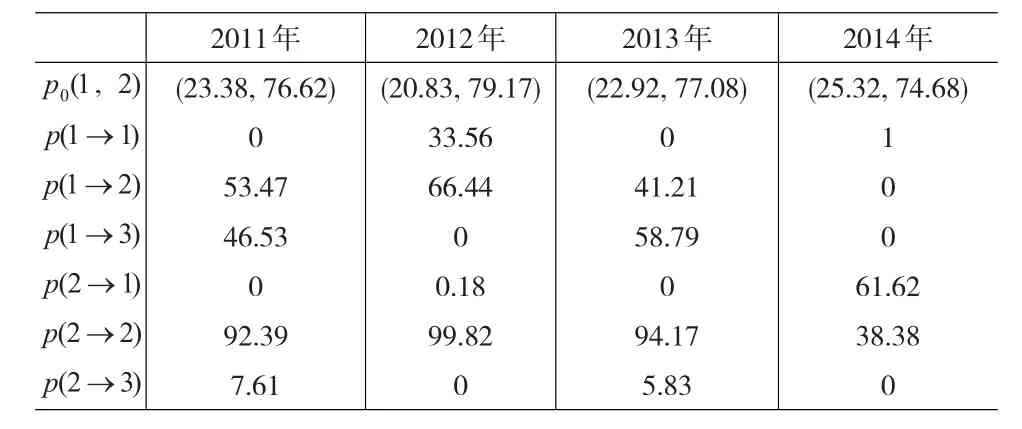
表4 初始概率与转移概率的计算结果（单位：%）

由表4可知：在下跌的市场（2011年）或震荡收跌的市场（2013年），转移概率相似，如果初始组合价值处于状态1，期末将有一半的概率跌到状态2，另一半概率跌到状态3（保险失败），如果初始组合价值处于状态2，则期末基本会维持在状态2；在震荡收涨的市场（2012年），如果初始组合价值处于状态1，将有约1/3的概率期末维持状态1剩下2/3的概率跌到状态2，如果初始组合价值处于状态2，则基本会维持在状态2；而在上涨的市场（2014年），若初始组合价值处于状态1，期末将会维持在状态1，若初始组合价值处于状态2，则将有约1/3的概率维持在状态2还有2/3的概率期末上升至状态1。

由计算可知，只要风险乘数大于7.9左右，则初始状态就位于状态1，它代表了使用了较高的金融杠杆，从而放大了风险头寸。金融杠杆的使用，在震荡收涨的市场（2012年）与上涨的市场（2014年）中可以保障本金安全前提下能取得较好的投资绩效。然而，在下跌的市场（2011年）或震荡收跌的市场（2013年）中高金融杠杆却可能导致组合保险失败。

因此，投资失败的主要原因是在市场下跌或震荡下跌的情况下决策者过于激进的风险偏好并选择了过高的风险乘数，从而放大了保险失败的缺口风险。

对于投资者来说，市场的趋势是投资组合保险失败与否的重要因素。但是无论什么样的市场，过度的风险头寸都是投资组合保险失败的诱因，尤其在预期下跌或震荡收跌的市场，风险乘数的设定存殁攸关。

3 结论

在存在融资约束之下，本文计算出投资组合价值在三种资产状态之间的转移概率矩阵，并推演出：风险乘数若增加，缺口风险将会上升；波动率若增加，缺口风险会上升；漂移率若增加，缺口风险会减少；无风险收益率若增加，缺口风险会增加；融资约束比率若增加，缺口风险会上升；若增加融资约束比率，投资更激进，缺口风险也会更大。

本文利用沪深300指数在2011—2014年这四个典型波动年份数据，计算出不可融资限制下最优的风险乘数和调整周期，从而为市场状况与投资组合策略的选择提供了实证参考。通过这四年的金融数据实证计算出不同初始状态的期末资产价值转移概率，从中可知，组合保险失败的主要原因是在市场下跌或震荡下跌的情况下决策者过于激进的风险偏好从而选择了过高的风险乘数，过度的风险头寸导致了保险失败。

[1]Black F,Jones R.Simplifying Portfolio Insurance[J].Journal of Portfolio Management,1987,14,(1).

[2]Merton R C.Continuous-Time Finance[M].New York:Basil Blackwell,1990.

[3]Black F,Andre F.Theory of Constant Proportion Portfolio Insurance [J].Journal of Economic Dynamic and Control,1992,(16).

[4]Khuman A,Dietmar M,Nick C.Constant Proportion Portfolio Insurance:Statistical Properties and Practical Implications[R].University of Essex,Working Paper,2008.

[5]Weng C G.Constant Proportion Portfolio Insurance Under a Regime Switching Exponential Levy Process[J].Insurance:Mathematics and Economic,2013,(52).

[6]程兵，魏先华.投资组合保险CPPI策略研究[J].系统科学与数学，2005，25(3).

[7]杜少剑,陈伟忠.CPPI投资组合保险策略的实证分析[J].财贸研究，2005，(1).

[8]黄丽清.CPPI策略缺口风险研究[D].上海：复旦大学，2009.

[9]徐竞.基于马尔科夫链的动态CPPI投资策略研究及实证[J].重庆理工大学学报：自然科学版，2012，26(4).

[10]周圣，史本山，段玉娟.基于离散时间交易下的CPPI策略[J].系统工程，2012，30(5).

（责任编辑/易永生）

F832

A

1002-6487（2017）11-0162-04

丁钊鹏（1978—），男，四川潼南人，博士研究生，讲师，研究方向：金融工程、债券及衍生品。刘立新（1966—），男，河北安国人，教授，博士生导师，研究方向：金融工程、风险管理。