预应力钢-混叠合梁剪力滞效应理论计算分析

罗婧文左 科王海涛

（1.招商局重庆交通科研设计院有限公司，重庆 400000；2.华蓝设计（集团）有限公司重庆分公司，重庆 400000；3.贵州城市职业学院，贵州 贵阳 550000）

预应力钢-混叠合梁剪力滞效应理论计算分析

罗婧文1左 科2王海涛3

（1.招商局重庆交通科研设计院有限公司，重庆 400000；2.华蓝设计（集团）有限公司重庆分公司，重庆 400000；3.贵州城市职业学院，贵州 贵阳 550000）

文章结合能量变分法、剪力滞叠加原理及荷载平衡法，分析了预应力钢-混叠合连续梁剪力滞系数的计算方法，并结合相关计算案例，利用有限元软件进行了验证分析，分析表明：计算值和有限元结果比较接近，从而验证了预应力钢-混叠合连续梁中剪力滞系数计算方法的可行性。

钢箱；预应力钢-混叠合梁；剪力滞系统；能量变分法；剪力滞叠加原理；荷载平衡法

随着我国桥梁技术的迅猛发展，桥梁结构形式逐渐变得多种多样，并且随着冶炼技术的发展，钢材的性能和产量也逐步提高。因此，钢结构桥梁的应用也越来越多，其中钢-混叠合梁由于能够同时发挥出钢材和混凝土的材料性能，近年来发展迅速。而预应力钢-混叠合连续梁除具有承受正弯矩简支叠合梁的优点外，还能够改善叠合连续梁中间支座区域的受力性能，减小中间支座负弯矩。本文利用能量变分法及叠加原理从理论上分析推导了预应力钢-混叠合连续梁的剪力滞效应，并且采用有限元软件进行了验证分析，同时对两者的结构差异进行对比。

1 基本理论

1.1 假定

（1）在不考虑钢箱中预应力钢束和混凝土面板中普通钢筋对刚度的影响下，通过荷载平衡法将预应力荷载等效为施加在钢-混叠合梁上的外荷载；（2）在弹性阶段，混凝土面板与钢箱梁完全协同工作，不考虑两者之间的相对位移。

1.2 相关公式

以图1所示的预应力钢-混叠合梁典型断面为例，引入叠合梁竖向位移函数纵梁位移函数u(x,y)可假定为：

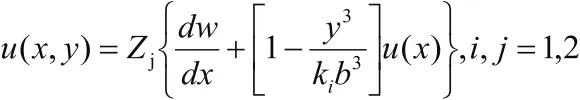
式中：u(x)为剪切转角的最大差值。

图1 钢-混叠合梁典型断面示意图

为剪力键之间混凝土的宽度；tu为混凝土板的厚度；h为叠合梁的总体高度。

根据参考文献[3]中推导波形钢腹板组合箱梁剪力滞效应的方法，易于推导出钢-混叠合梁受弯时的荷载势能钢箱梁应变能剪力钉之间混凝土的应变能混凝土翼缘板的应变能体系的总势能最终根据变分法中的最小势能原理得到由位移函数表示的控制微分方程如下：

边界条件为：

求解u(x)，可以得到考虑剪力滞效应后的混凝土板的应力为：

2 剪力滞效应理论计算公式

2.1 预应力布置及等效荷载工况

本文以两跨等跨预应力连续梁为例，钢-混叠合连续梁中的预应力通过体外束实现，布置方式如图2所示，其中体外预应力束在钢箱内的转向通过在转向位置设置钢横隔板来实现。体外束原则上应在正负弯矩交界点及正弯矩最大值位置实现转向，最后在两端头的锚固位置恰好通过组合截面的形心轴，这样能充分发挥体外预应力的效果。预应力钢-混叠合连续梁中的1-1和2-2断面如图3所示。

图2 叠合梁中预应力束布置方式

图3 叠合梁断面图

为了便于考虑叠合梁上的荷载作用，结合上述叠合梁中体外预应力束的布置特点，预应力荷载可以利用荷载平衡法原理等效为作用于叠合梁上的集中力，同时钢箱梁的自重也可以等效为均布荷载，再加上中支座处的支座反力可以求得，最终叠合梁上的荷载作用均可等效简化为作用于简支梁上的外荷载，具体如图4简化所示。

图4 叠合连续梁等效荷载图示

2.2 等效荷载工况下的剪力滞系数计算

图5 六种工况的受力图

由于梁端预应力等效荷载的竖向分力直接传入支座，同时水平分力又恰好通过叠合梁的形心轴而不产生任何偏心弯矩，故在计算剪力滞系数时不考虑梁端预应力荷载。因此在计算上述等效荷载作用下的剪力滞系数时，可以将原等效荷载体系分解为图5中的六种荷载工况进行叠加。定相似性最终可归结为均布荷载作用于简支梁和集中荷载作用于简支梁两种情况下的剪力滞系数求解。

第一，均布荷载q作用下（工况1）的剪力滞系数。考虑剪力滞效应后，可以求得混凝土板任一截面位置x处的正应力为：

而按初等梁理论的任一截面应力为：

第二，集中荷载P作用下（工况2-6）的剪力滞系数。考虑剪力滞效应后，可以求得混凝土板任一截面位置x处的正应力为：

式（6）和式（7）中a为集中荷载作用位置，工况6中a的取值参照图5，式中l=2L。

工况6的剪力滞系数为：

2.3 计算公式

各等效荷载工况下的剪力滞系数求得后，根据参考文献[2]所介绍关于求解剪力滞效应的叠加原理，可求得预应力钢-混叠合连续梁中计算截面的剪力滞系数为：

式（9）中：M为计算截面的弯矩；Mi为基本结构在单一荷载作用下，在计算截面上的弯矩；W为计算截面的截面模量；l为超静定结构中计算截面的剪力滞系数；il为在基本结构中，在单一荷载下计算截面的剪力滞系数。

3 有限元对比分析

3.1 计算案例

计算案例跨径为2×6m，全长12m，梁总高h＝500mm，混凝土面板厚100mm，混凝土面板的有效宽度1000mm，混凝土翼板为C40现浇混凝土板，钢箱梁高400mm，顶底板及腹板厚度均为8mm，钢箱内横隔板尺寸均为PL10×384×384mm，钢材为Q235，采用直径为13mm的圆钉柱头剪力钉作为剪力连接件，沿梁纵向间隔150mm等间距布置。预应力筋采用两束3φ5的钢绞线，计算案例立面及断面如图6所示：

图6 预应力钢-混叠合连续梁结构尺寸（单位：mm）

3.2 有限元分析

有限元计算采用ABAQUS软件进行模拟计算分析，模型中混凝土板采用C3D8I模拟，钢箱梁采用S4R模拟，预应力束及钢筋采用T3D2。模型中只考虑了预应力钢-混叠合连续梁的自重和预应力的作用，不考虑混凝土收缩徐变、温度等其他外荷载的作用。叠合连续梁的几何模型和有限元模型如图7所示：

图7 叠合连续梁几何和有限元分析模型

3.3 结果对比

根据计算，预应力钢-混叠合连续梁剪力滞系数理论计算及有限元计算结果见表1，理论计算值与有限元计算值对比计算表见表2。

通过表1、表2的对比结果可以看出，本文所述理论计算方法的结果与有限元计算结果大致接近，总体上理论计算结果比有限元计算结果偏大，从而利用有限元相对精确的计算结果验证了上述理论计算方法的可行性。

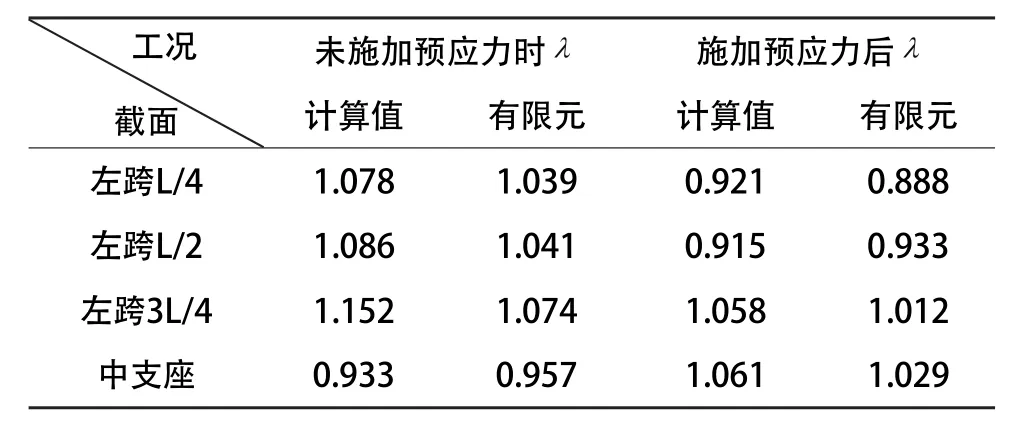
表1 预应力叠合连续梁剪力滞系数理论值和有限元对比

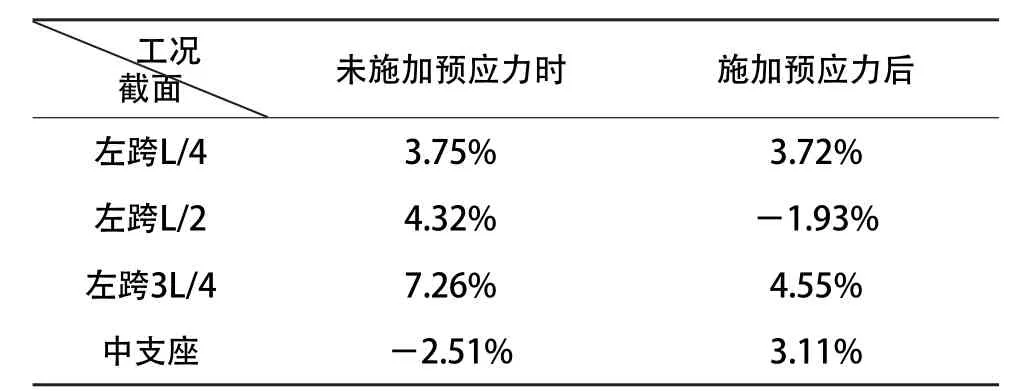
表2 理论值对比有限元值相对偏大比例

对比结果还反映出，在未施加预应力时，钢-混叠合连续梁中混凝土板中部的最大剪力滞系数均出现在左跨3/4截面处；施加预应力后，最大剪力滞系数则出现在左跨1/4截面处。从而表明施加预应力后，混凝土板的应力发生重分布，靠近连续梁中支座区域的混凝土板应力较未施加预应力时均匀；靠近边支座区域的混凝土板应力没有未施加预应力时均匀，出现一定的应力集中现象。

由于施加预应力后的剪力滞系数和预应力筋的布置形式、截面形式和跨径布置等都有很大关系。本文针对预应力钢-混叠合连续梁所讨论的剪力滞效应计算方法有一定的特殊性，但是此种剪力滞效应计算方法的思路还是具有普遍规律性的，可以供类似工程参考。

4 结语

（1）本文结合能量变分法、剪力滞叠加原理及荷载平衡法，分析了预应力钢-混叠合连续梁中混凝土板剪力滞系数的计算方法；（2）通过利用有限元对预应力钢-混叠合连续梁模拟分析，可以看出上述计算方法的计算结果接近有限元计算结果，从而利用有限元相对精确的计算结果验证了上述理论计算方法的可行性。

[1]王连广．钢与混凝土组合结构理论与计算[M]．北京：科学出版社，2005.

[2]张士铎．箱形薄壁梁剪力滞效应[M]．北京：人民交通出版社，1998.

[3]李立峰，彭鲲，王文．波形钢腹板组合箱梁剪力滞效应的理论与试验研究[J]．公路交通科技，2009，26（4）.

[4]林同炎．预应力混凝土结构设计[M]．北京：中国铁道出版社，1983.

（责任编辑：小 燕）

U442

1009-2374（2017）07-0167-03

10.13535/j.cnki.11-4406/n.2017.07.079

罗婧文（1987-），女，四川人，招商局重庆交通科研设计院有限公司工程师，研究方向：桥梁设计、桥梁抗震、桥梁检测。

A