混联式汽车电泳涂装输送机构同步滑模控制
高国琴, 吴欣桐, 曹园园, 方志明
(江苏大学 电气信息工程学院,江苏 镇江 212013)
混联式汽车电泳涂装输送机构同步滑模控制
高国琴, 吴欣桐, 曹园园, 方志明
(江苏大学 电气信息工程学院,江苏 镇江 212013)
针对一种新型混联式汽车电泳涂装输送机构,为解决其运动过程中各关节之间的同步协调控制问题,采用拉格朗日法建立其动力学模型,并基于该动力学模型和输送机构的结构特点,提出一种同步误差,该同步误差不仅包括关节自身的误差信息,还包括关节之间的误差信息。在此基础上,将交叉耦合控制技术与滑模变结构控制相结合,提出一种同步滑模控制策略,并运用Lyapunov稳定性理论证明了所提出控制算法的稳定性。最后通过仿真与常规滑模控制进行比较,结果表明,所设计同步滑模控制器响应速度快,跟踪误差小,实现了汽车电泳涂装输送机构的稳定跟踪运动控制,同时提高了其同步协调性。
混联机构;动力学模型;滑模控制;同步控制;耦合误差
0 引 言
目前现有工业机器人大多为串联机构,串联机构结构简单,易于工业制造。与串联机构相比,并联机构具有累计误差小、刚度重量比大、动态特性好、结构紧凑、承载能力强、结构抗震性好和运动惯量小等优点[1],但也存在工作空间小、结构尺寸偏大、传动环节过多等缺陷,影响了其实际应用。混联机构结合了串联和并联机构的优点,具有可控自由度高、工作空间大、速度快、刚性高、造价低等众多优点[2]。基于此,本课题组新研发了一种新型混联式汽车电泳涂装输送机构[3]。
与基于运动学模型的控制器相比,基于动力学模型的控制器由于考虑了混联机构的动力学特性,因此能获得更好的控制性能[4]。但是对一般混联机构而言,动力学建模较为复杂,难以获得准确的动力学参数,系统存在不确定性问题[5]。传统的动力学控制方法如PD控制和计算力矩控制一般不能有效解决其不确定性问题,而滑模变结构控制因具有对外界干扰和系统参数变化不敏感、能够快速响应、无需在线进行参数辨识等优点[6],有望有效解决具有不确定性的混联机构的控制问题。
混联机构中的并联机构为多支路的闭链结构,各支路间通常存在耦合作用,因此各支路执行机构间的同步协调性影响着系统的整体性能。目前,在具有多执行机构的并/混联机构及其装备的控制器设计中,各执行机构的控制回路仅接收所控关节的局部反馈信息,没有来自与其他执行机构相对应的其他关节的反馈信息,因此,某个执行机构的控制回路中的干扰所引起的误差,仅在该回路得以纠正,其他控制回路并不响应。由于并/混联机构的末端轨迹由所有执行机构的运动决定,因此所有主动关节应同步控制才能高精确度地跟踪期望轨迹,否则跟踪精确度会由于各主动副运动的不协调而有所降低,严重时,如主动副具有高加速度时,甚至损坏机械结构[7]。本文所研究的以两边对称结构形式实现汽车电泳涂装输送的混联机构,对其同步协调性有着更高的要求。为此,为实现新型混联式汽车电泳涂装输送机构的高性能控制,本文在设计混联机构控制策略时,通过引入同步控制理论,并与滑模控制理论相结合,以在实现对混联机构稳定跟踪控制的同时进一步提高系统的同步协调性能。
经典同步控制理论于20世纪80年代由Robert.D.Lorenz[8]和Y.Koren[9]提出,主要分为并行控制、主从控制、交叉耦合控制[10]。交叉耦合同步控制技术首先针对双轴运动平台而提出[11]。这种同步控制方法通过引用子系统之间的速度或角度相对差作为一个额外的反馈信号[12],以改善被控子系统间的相互运动同步,从而提高双轴跟踪精确度,该方法已成为同步运动控制的标准模式。对于本文研究的对同步协调性有着较高要求的汽车电泳涂装输送混联机构而言,并行控制的控制精确度较低,同步性能较差;主从控制在从动端跟踪主动端的过程中会不可避免产生信息传递滞后;而交叉耦合控制的特点与两组升降翻转机构的动力学特性相吻合,因此本文采用交叉耦合控制形式。
基于上述分析,本文以本课题组设计的新型混联式汽车电泳涂装输送机构的升降翻转机构为研究对象,首先基于拉格朗日法求得其动力学模型,并转化为关节空间动力学模型;然后针对该机构的结构特点及运动特点,提出一种同步误差,将该同步误差与关节跟踪误差相结合得到耦合误差,通过将该耦合误差与滑模控制相结合,进一步提出一种同步滑模控制算法,最后通过Matlab仿真试验验证其算法的正确性和有效性。
1 电泳涂装输送机构动力学分析
1.1 电泳涂装输送机构描述
新型混联式汽车电泳涂装输送机构结构图如图1所示,其中1为第一驱动器,2为第一丝杠,3为第二丝杠,4为导轨,5为第一滑块,6为第一转动副,7为第一连杆,8为第二转动副,9为第二滑块,10为第三转动副,11为第二连杆,12为第二驱动器,13为主动轮,14为皮带,15为从动轮,16为连接杆,17为车体固定架,18为车体,19为行走驱动器,20为行走底座,21为导向轮,22为第一行走轮,23为第二行走轮,24为导轨。该机构包括行走机构和升降翻转机构两个功能部分。行走机构通过行走驱动器同步驱动行走轮在导轨上运动,从而实现输送机的行走运输功能。升降翻转机构固定在行走底座上,由两组结构相同的升降翻转机构组成,两组升降翻转机构通过连接杆与车体固定架相连,连接杆位于行走机构的上方,车体固定架与连接杆相互固定。升降翻转机构包括升降部分和翻转部分。第一驱动器通过传动机构将驱动器的运动传递到丝杠上,第一滑块与第二滑块通过丝杠以丝杠螺母副驱动,两滑块相互靠近或远离,车体产生相应的上升或下降运动。翻转部分固定在第一连杆上,第二驱动器驱动主动轮运动,主动轮通过皮带带动从动轮运动,从而使车体实现翻转功能。
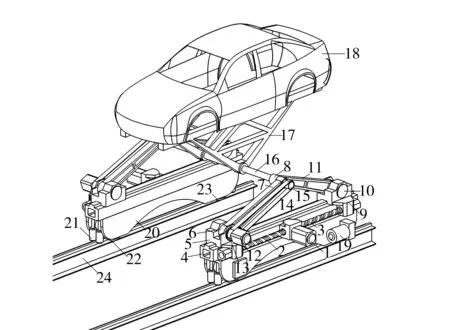
图1 汽车电泳涂装输送机构结构图Fig.1 Structure of a mechanism for automobile electro-coating conveying
由于行走机构与升降翻转机构两部分相对独立,其中,行走机构的控制相对简单,而升降翻转机构为输送机的主体机构,对输送机性能的影响较大,且其控制要求相对较高。因此以其升降翻转机构为研究对象,其结构简图如图2所示。以如图2所示升降翻转机构所在位置为绝对零位,在该位置下第一驱动器1处建立系统静坐标系,Pi(i=1,2)为连接杆两端的运动副位置,Bj(j=1,2,3,4)为四个滑块位置。

图2 升降翻转机构的结构简图Fig.2 Structure of the lifting-flipping mechanism
1.2 笛卡尔空间的动力学模型
采用拉格朗日方法建立升降翻转机构的动力学模型。拉格朗日法是以系统动能和势能为基础建立动力学方程,推导过程比较简单,形式较为简洁。选取连接杆中点的位姿参数q=(z,β)T作为系统广义坐标,其中z为连接杆中点在Z轴方向的位移;β为连接杆中点绕y轴逆时针转动的角度。根据参考文献[13]的动力学模型建立过程,可得动力学模型的最终结果为

(1)




4ma)Δ1+0.5ml1+0.5ml2+2mb+ml3,
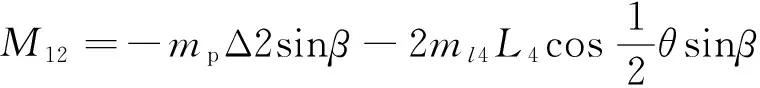

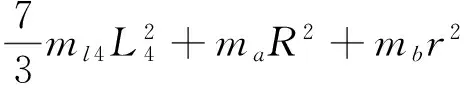




G11=(mp+4ml4+ml1+ml2+ml3+2mb)g,


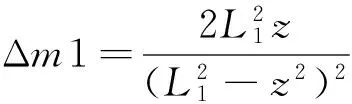
式中:mp是车体18的质量;ml1、ml2、ml3分别为第一连杆7、第二连杆11、连接杆16的质量;ml4是车体固定架上支架的质量;m1、m2分别为第一滑块5和第二滑块9的质量;ma、mb分别为主动轮13与从动轮15的质量;a、b、c分别为车体长宽高;rl3为连接杆16的半径;r1、r2分别为从动轮15半径和主动轮13半径;L1、L2分别为第一连杆7和第二连杆11的长度;L4为车体固定架17上斜支架的长度;θ为车体固定架17上两条斜杆之间的角度。
(2)

方程(2)是以连接杆中点位姿参数q=(z,β)T为系统广义坐标建立的,因此,方程中的Q为分别作用在(z,β)方向上的广义力或广义力矩。为了将广义力或广义力矩转化为关节驱动力或驱动力矩,需要做如下变换
Q=JTτ。
(3)
式中:J为升降翻转机构的雅各比矩阵,τ为关节驱动力或驱动力矩向量。
1.3 关节空间的动力学模型
由于设计的控制器需考虑主动关节之间的同步误差,因此需将笛卡尔空间的动力学模型转换到关节空间。
连接杆中点位姿速度、加速度与主动关节速度、加速度具有如下关系:

(4)

(5)
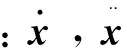
将式(3)~式(4)代入式(2),经整理后可得到动力学方程中各参量由笛卡尔空间到关节空间的转换关系:
M(x)=[J(q)T]-1M(q)J(q)-1,
(6)
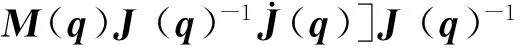
(7)
G(x)=[J(x)T]-1G(q)。
(8)
进一步得到在关节空间内的升降翻转机构的动力学方程:

(9)

2 同步误差的建立
同步误差代表了主动关节之间的协调关系,它不同于传统的跟踪误差,不仅包含了关节自身的误差信息,同时也包含了关节之间的误差信息[16]。
六个主动关节(四个滑块和两个主动轮)的位置跟踪误差可表示为:
(10)
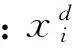
(11)
则说明每个关节同步,由此定义各相应关节之间的同步误差为:
(12)
式中:εi(t)(i=1,2…6)分别为新型输送机构六个主动关节间的同步误差。
根据式(12)可得同步误差的表达式为
ε(t)=H1e(t)。
(13)
式中:
e(t)=[ex1(t),ex2(t),ex3(t),ex4(t),eφ1(t),eφ2(t)]T,

3 同步滑模控制器设计
(14)
由于研究的新型混联式汽车电泳涂装输送机构,不仅要实现被控系统的稳定跟踪,而且需有较好的同步协调性。因此,将关节跟踪误差e(t)与同步误差ε(t)相结合,定义耦合误差e*(t)为

(15)
式中λ=diag(λ1,λ2,λ3,λ4,λ5,λ6),是对角正定耦合参数矩阵。
设计滑模面为
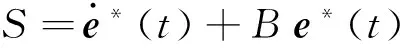
(16)

同步滑模控制律设计如下。
对式(16)中的S求导,并将式(15)代入得

(17)
由式(9)可得
G(x)-D(t)-F(t))。
(18)
取等速趋近律

(19)
式中:K=diag(k1,k2,k3,k4,k5,k6),ki>0(i=1,2,…6)。常数矩阵K表示系统的运动点趋近切换面S=0的速率。ki小,趋近速度慢;ki大,则趋近速度快,但引起的抖振也较大。
将式(18)和式(19)代入式(17)整理得同步滑模控制律为:
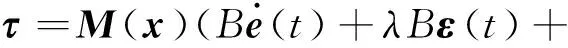

(20)
下面证明所设计同步滑模控制算法的稳定性。
设Lyapunov函数为

(21)
式中S=[s1,s2,s3,s4,s5,s6]T。

-STKsgn(S)。
(22)
式中:

diag(sgn(s1),sgn(s2),sgn(s3),sgn(s4),sgn(s5),
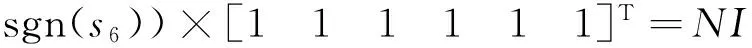
(23)
将式(23)代入式(22)得:


根据Lyapunov稳定性定理,可见所设计控制算法稳定。
4 仿真试验及结果分析
为验证所设计控制算法的正确性和有效性,以升降翻转机构的动力学模型为被控对象,分别对滑模控制器、同步滑模控制器进行MATLAB仿真。根据样机设计,升降翻转机构的各物理参数为:mp=17 kg,ml1=3.5 kg,ml2=1.5 kg,ml3=3 kg,ml4=0.5 kg,m1=m2=2 kg,ma=0.5 kg,mb=0.25 kg,a=0.65 m,b=0.56 m,c=1.125 m,rl3=0.015 m,r1=0.05 m,r2=0.03 m,L1=0.311 m,L4=0.65 m,θ=120° 。粘性系数矩阵Bc为diag(0.7,0.7,0.7,0.7,0.9,0.9),库仑摩擦力矩阵Fc为diag(3.5,3.5,3.5,3.5,4.1,4.1),外界干扰F(t)为3sin(2πt)。选取滑模面及控制器参数分别为:B=diag(9,9,9,9,10,10),K=diag(10,10,10,10,20,20),λ1=diag(10,10,10,10,10,10)。主动关节x的初始位姿为(0.1 m,-0.1 m,0.1 m,-0.1 m,0 rad,0 rad)。为检验新型混联式输送机构在所设计控制器作用下的同步协调性,改变惯性矩阵为M′(x)=M(x)+m(x),其中m(x)=(0.1,0.2,0.3,0.2,0.5,0.6)),得到系统仿真结果如图3~图5所示。

图3 连接杆中点位姿各分量轨迹跟踪误差曲线Fig.3 Trajectory tracking errors of the connecting rod’s midpoint in all directions
图3为连接杆中点位姿各分量的轨迹跟踪误差曲线,通过比较得到连接杆中点位姿各分量分别在趋近律滑模控制和同步滑模控制作用下由初始状态到稳定状态的时间,如表1所示。另外,在趋近律滑模控制作用下,当系统到达稳定状态后,z方向上的系统稳态误差绝对值最大为5.69×10-4m,β的稳态误差绝对值最大为6.12×10-4rad;在同步滑模控制作用下,当系统到达稳定状态后,z方向上的系统稳态误差绝对值最大为3.78×10-6m,β的稳态误差绝对值最大为3.73×10-4rad。结果表明:由于提高了系统的同步协调性,同步滑模控制使混联式输送机构末端(连接杆)的运动控制具有更快的响应速度和更高的跟踪精确度。

表1 连接杆中点位姿各分量由初始状态到稳定状态的时间

图4 单边升降翻转机构三个主动关节的轨迹跟踪误差Fig.4 Trajectory tracking errors of three active joints of single side of lifting-flipping mechanism
图4 为单边升降翻转机构三个主动关节的轨迹跟踪误差,由图4分析比较,得到三个主动关节分别在趋近律滑模控制和同步滑模控制作用下由初始状态到稳定状态的时间如表2所示,表2结果表明,所设计的同步滑模控制方法有效提高了主动关节的响应速度。另外,由图4可以看出,在趋近律滑模控制作用下,当系统到达稳定状态后,第一滑块的系统稳态误差绝对值最大为3.32×10-4m,第二滑块的系统稳态误差的绝对值最大为3.31×10-4m,主动轮的稳态误差绝对值最大为1.02×10-3rad;在同步滑模控制作用下,当系统到达稳定状态后,第一滑块的系统稳态误差绝对值最大为1.87×10-4m,第二滑块的稳态误差绝对值最大为1.87×10-4m,主动轮的稳态误差绝对值最大为5.94×10-4rad。结果表明:由于提高了系统的同步协调性,同步滑模控制使各主动关节的运动控制具有更快的响应速度和更高的跟踪精确度。

表2 单边机构主动关节由初始状态到稳定状态的时间
图5为两组升降翻转机构各对应主动关节之间的同步误差曲线图,对比分析在两种控制器作用下的图5表明,在同步滑模控制器作用下,两组升降翻转机构各对应主动关节之间的同步误差较小,该控制方法有效提高了主动关节之间的协调性。
为了进一步比较两种控制器的轨迹跟踪性能,选取连接杆中点位姿的跟踪均方根误差(tracking RSME of the link’s midpoint, L-M-RSME)作为性能指标,即:

式中:ez(j)和eβ(j)分别表示连接杆中点位姿在第j个点的在z方向的跟踪误差和β的跟踪误差。
同理可定义主动关节的跟踪均方根误差(trackingRSMEoftheactivejoint,AJ-T-RSME)为:
同步误差的均方根误差(SynchronizedRSME)为

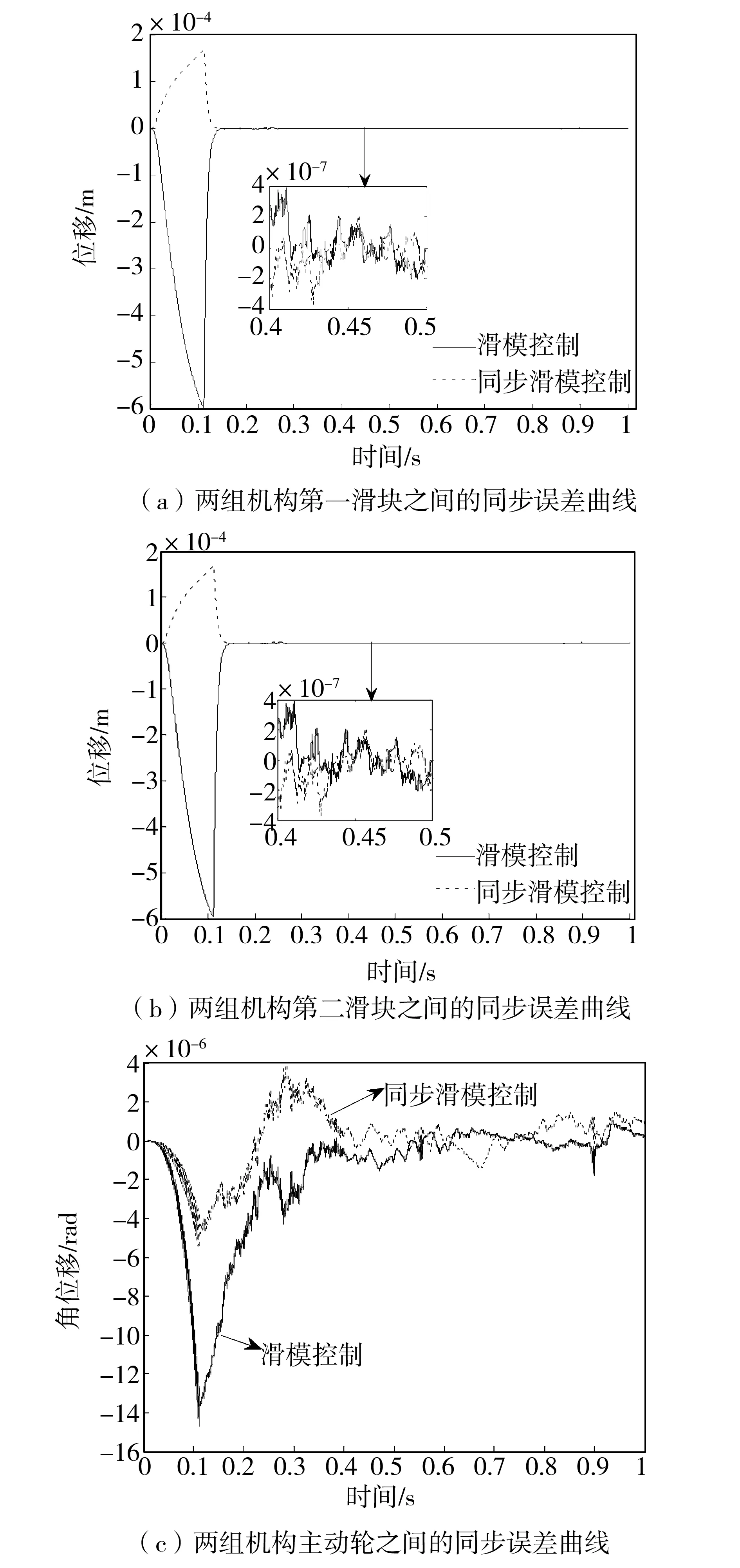
图5 两组升降翻转机构三个主动关节之间的同步误差曲线Fig.5 Synchronized errors of three active joints between two lifting-flipping mechanisms
在两种控制器作用下主动关节的各均方根误差如表3所示,由表3可见,采用同步滑模控制,能够降低主动关节的位置跟踪误差和主动关节之间的同步误差,因此有效提高了连接杆中点位姿的运动跟踪精度。

表3 在两种控制器作用下主动关节的均方根误差
5 结 论
本文以本课题组研发的新型混联式汽车电泳涂装输送机构为研究对象,着力实现对该机构的稳定跟踪运动控制,并同时提高系统的同步协调性能。
本文的主要贡献有:
1)分析建立该机构中升降翻转机构的笛卡尔动力学模型和关节空间动力学模型,针对该机构的结构特点及运动特点,提出一种同步误差,将该同步误差与关节跟踪误差相结合得到耦合误差,并与滑模控制相结合。
2)提出一种同步滑模控制方法。通过与常规滑模控制方法进行仿真比较,结果表明,该方法不仅能使系统具有更高的跟踪精确度和更快的响应速度,而且具有更小的同步误差,从而能实现两组升降翻转机构主动关节的同步运动,提高了输送机构的同步协调运动控制性能。
[1] PI Yangjun, WANG Xuanyin, GU Xi. Synchronous tracking control of 6-DOF hydraulic parallel manipulator using cascade control method[J]. Journal of Central South University of Technology, 2011,18(5):1554-1562.
[2] 姜铭, 孙钊, 秦康生, 等. 混联机器人的分析与研究[J]. 制造业自动化. 2009,31(1):61-65. JIANG Ming, SUN Zhao, QIN Kangsheng, et al. Study on serial-parallrel mechanisms[J]. Manufacturing Automation,2009,31(1):61-65.
[3] 刘辛军, 陈祥, 高国琴. 一种三自由度汽车涂装输送机[P],中国:201210015045.7, 2012.1.18.
[4] 赵钢, 刘娟. 一种基于干扰观测器的重复控制解耦方法[J]. 哈尔滨理工大学学报, 2012, 17(6):25-29. ZHAO Gang, LIU Juan. A repetitive control decoupling method based on disturbance observer[J]. Journal of Harbin University of Science and Technology, 2012, 17(6):25-29.
[5] 武俊峰, 孙雷. 两轮自平衡机器人的控制方法研究[J]. 哈尔滨理工大学学报, 2014, 19(6):22-26. WU Junfeng, SUN Lei. Two-wheeled self-balancing robot control method study[J]. Journal of Harbin University of Science and Technology, 2014, 19(6):22-26.
[6] 武俊峰, 李月. 滑模变结构方法在两轮自平衡机器人上的应用[J]. 哈尔滨理工大学学报, 2013, 18(2):95-100. WU Junfeng, LI Yue. The reseach on the application of two-wheeled self-balancing robot based on the method of variable structure control[J]. Journal of Harbin University of Science and Technology, 2013, 18(2):95-100.
[7] SUN Dong, LU Ren,MILLS J K,et al. Trajectory tracking control for a 3-DOF planar parallel manipulator using the convex synchronized control method[J]. The International Journal of Robotics Research, 2006,25(11):1137-1147.
[8] LORENZ R D,SCHMIDT P B.Synchronized motion control for process automation[C]//IEEE proceedings of the 1989 IEEE Industry Application Annual Meeting, 1989,02:1693-1698.
[9] KOREN Y.Cross-coupled biaxial computer control for manufacturing systems[J]. Journal of Dynamic Systems Measurement & Control, 1980,102(4):265-272.
[10] 曹玲芝, 李春文, 牛超,等. 基于相邻交叉耦合的多感应电机滑模同步控制[J]. 电机与控制学报, 2008, 12(5):586-592. CAO Lingzhi, LI Chunwen, NIU Chao, et al. Synchronized sliding-mode control for multi-induction motors based on adjacent cross-coupling[J]. Electric Machines and Control, 2008, 12(5):586-592.
[11] REN Lu,SUN Dong,MILLS J K,et al.Synchronous tracking control of parallel manipulators using cross-coupling approach[J]. Journal of Dynamic Systems Measurement & Control,2005,128(4):976-979.
[12] PEREZ PINAL F J,NUFIEZ C,ALYAREZ R,et al.Comparison of multi-motor synchronization techniques[C]//The 30th Annual Conference of the IEEE Industrial Electronics Society. 2004, 02:1670-1675.
[13] 牛雪梅,高国琴,刘辛军,等.新型驱动冗余并联机构动力学建模及简化分析[J].机械工程学报,2014,50(19):41-49. NIU Xuemei, GAO Guoqin, LIU Xinjun, et al. Dynamic formulation and simplified model of a novel 3-DOF parallel mechanism with actuation reduntancy[J]. Journal of Mechanical Engineering, 2014,50(19):41-49.
[14] 尚伟伟.平面二自由度并联机器人的控制策略及其性能研究[D].合肥:中国科学技术大学,2008.
[15] ALBERTO I.Nonlinear control system[M].Berlin:Spring-Verlag,1995.
[16] WANG Can, SUN Dong. A synchronization control strategy for multiple robot system using shape regulation technology[C]//7th World Congress on Intelligent Control and Automation.2008WCICA,2008:467-472.
(编辑:贾志超)
Synchronized sliding mode control of a hybrid mechanism for automobile electro-coating conveying
GAO Guo-qin, WU Xin-tong, CAO Yuan-yuan, FANG Zhi-ming
(School of Electrical & Information Engineering, Jiangsu University, Zhenjiang 212013, China)
For a hybrid mechanism for electro-coating conveying, in order to solve the synchronization problems between the active joints, the dynamic model of the hybrid mechanism was firstly formulated by Lagrange method. Next, a synchronized error was proposed based on the mechanism’s characteristics and the dynamic model. The synchronized error contained not only the error of the joint itself, but also the error between the active joints. Then, a synchronized sliding mode control was proposed by incorporating a coupled error into a sliding mode control, and its stability was proved by Lyapunov stability theory. Finally, compared with a conventional sliding mode controller, simulation results show that the synchronized sliding mode controller not only has the faster response speed and the smaller tracking error, but also achieves the stability of tracking control, and improves the synchronous coordination of the mechanism.
hybrid mechanism; dynamic model; sliding mode control; synchronized control; coupled error
2015-02-04
国家自然科学基金(51375210);江苏高校优势学科建设工程资助项目;镇江市工业科技支撑计划(GY2013062);镇江市京口区科技计划项目(jkGY2013002)
高国琴(1965—),女,教授,博士生导师,研究方向为并联机构及其装备的控制; 吴欣桐(1990—),女,硕士研究生,研究方向为并联机构的滑模控制; 曹园园(1992—),女,硕士研究生,研究方向为混联机构的同步协调控制; 方志明(1978—),男,博士,讲师,研究方向为并联机构的控制。
高国琴
10.15938/j.emc.2017.06.015
TP 27
A
1007-449X(2017)06-0113-08

