小波降噪及Hilbert变换在电机轴承故障诊断中的应用
丁锋, 秦峰伟
(西安工业大学 机电工程学院,陕西 西安 710021)
小波降噪及Hilbert变换在电机轴承故障诊断中的应用
丁锋, 秦峰伟
(西安工业大学 机电工程学院,陕西 西安 710021)
针对振动信号降噪处理及故障特征提取是机械故障诊断的重点问题,为了有效消除高频信号的影响,并充分提取出电机轴承的低频故障特征。提出利用小波降噪及Hilbert变换的方法对采集的电机轴承振动数据进行处理并提取其故障特征信息。首先,运用小波降噪对采集到的振动数据进行降噪处理,抑制噪声干扰,然后对其进行Hilbert变换解调出故障特征频率。通过对现场测取的轴承振动数据进行信号处理可以达到理想的诊断效果,由此得知,该方法能通过电机轴承振动信号进行故障特征信息处理,有效地进行轴承故障分析及诊断。
轴承;振动信号;小波消噪;Hilbert变换
0 引 言
轴承作为机械中最常见的机械零部件之一,是机械设备转子系统中最重要的组成部分,其运行状态直接影响着整个系统的工作状态。轴承故障诊断是转子系统诊断的重点之一,据相关数据表明,在旋转机械故障中,由于轴承的失效至少引起了40%的机械故障,尤其在电机的故障中,轴承失效率占到了一半以上,苛刻的工作环境和复杂的工作状态使得转子系统中的轴承成为最易出现故障的环节。因此,运用一定的技术手段对轴承进行故障诊断是极其必要的[1-2]。
传统的轴承故障诊断是基于傅里叶变换,但傅里叶变换适用于平稳故障信号的分析,设备正常运行时,轴承的振动信号相对平稳,但设备由正常运行到故障是一个突变过程,所以是一个非平稳信号,由于噪声信号的影响,有用的故障特征信息很难被提取,如果直接将信号从时域转变为频域也不能作为一种理想的分析方法。Hilbert变换具有解调和细化谱分析功能,在实际中得到了广泛的应用,小波分析能够有效处理非平稳信号,是一种相对较为理想的方法[3]。针对传统旋转机械轴承振动故障诊断的不足,提出了小波降噪及希尔伯特变换的方法,提高并改善了现有的单纯依靠小波或者希尔伯特变换来进行处理分析的手段,并采集了惠普某型号电机轴承工作运行状态下的振动信号,运用该方法来进行信号处理分析,提取故障特征信息,并结合轴承故障特征频率的理论计算公式,有效地进行了轴承故障诊断。
1 小波分析降噪及Hilbert变换
傅里叶变换(fast Fourier transform, FFT)作为一种传统的信号处理方法,可以从频域的角度来观测信号,这样更能容易进行分析及故障诊断。但傅里叶变换是一种全局性的变换,并不能细致地展现出信号的局部特性,而时域信号局部细节信息包含了丰富的故障相关信息,在实际应用中,很难达到有效的分析效果,已经不能满足实际要求[4]。短时傅里叶变换(short time Fourier transform, STFT)则克服了以上的缺点,具有一定的局域化分析能力,但其无法同时考虑时间和频率的分辨率,且一旦其时域和频域窗口被选定,就不能再变化,即不具有自动调节功能,所以也不能作为一种理想的信号处理方法,而小波分析结合Hilbert变换可以作为对振动信号进行处理的理想手段。
1.1 小波分析及降噪
1.1.1 小波分析
小波变换具有短时傅里叶变换可以进行局域化分析的优点,窗口大小和形状可以根据实际处理需要进行调节,时间分辨率随着信号的频率的不同而进行自动调节。当窗口变长时,可以用来获取信号低频部分信息;当窗口变短时,则可以用来获取信号高频部分信息,即具有“自适应”功能,也就是具有自动调节的特性[5]。
小波是经过对基本小波函数进行尺度变换而得到的,基本小波是构成小波函数的基础,可以对信号进行多尺度分析,具有振荡快速衰减和紧支集的特点,满足小波容许性条件。
对基本小波函数进行伸缩和平移可以得到小波基函数,表示为
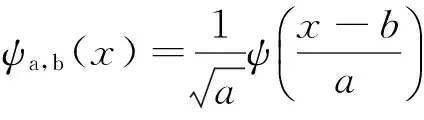
(1)
连续小波变换定义为
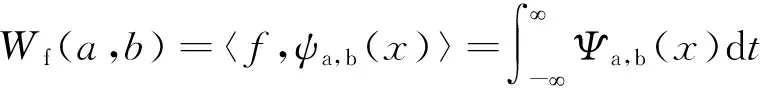
(2)
实际中一般对小波进行离散化处理才有意义,离散化指的是对小波函数的伸缩和平移尺度进行离散的。这种小波函数可表示为
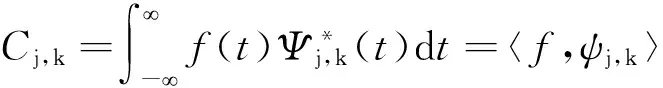
(3)
信号处理往往以特定的频段来进行小波重构,重构公式为
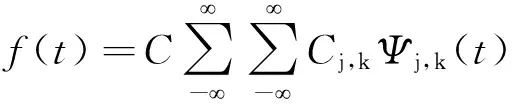
(4)
1.1.2 小波降噪
在实际应用时,由于设备振动信号包含各种噪声干扰,严重影响了故障分析,因此有必要先消除其中所含噪声。传统的信号降噪方法主要是利用各种滤波器进行滤波降噪的方法,如高低通滤波器及带通滤波器等,通过滤除噪声所在的频段达到降噪目的,但传统降噪方法使信号变换后的熵变大,信号的非线性特性也不能被很好地刻画,不是一种理想的处理手段,而小波变换则能解决传统信号降噪所存在的不足[6]。
小波变换具有信号低熵性、多分辨率、去相关性以及选基的灵活性的特征,这些特征使得基于小波变换的信号降噪处理成为一种有效的手段。在实际应用当中,有用信号一般为低频部分,而噪声一般则在高频部分[7]。小波降噪的思想就是处理小波分解中系数,然后对其进行重构达到降噪目的。小波降噪作为一种有效的信号处理方法,在实际应用当中发挥着重要作用。阈值降噪函数作为小波降噪函数的方法之一,相比其他效果更好、实现简单。进行阈值降噪就是通过设定一定的阈值,然后以这个阈值去处理小波分解的系数,反变换出原信号,从而重构出消除干扰后的信号。
进行小波降噪的阈值获取函数主要多种,其中,Thselect函数是一种自适应的阈值获取函数,可以依据不同形式的信号噪声干扰来自动调节阈值的大小,使得其优于一般降噪函数,处理效果较为理想,在实际应用中也得到了广泛的应用,故采用此函数进行降噪处理振动信号。
1.2 Hilbert变换
Hilbert变换可以提取时域信号的包络谱并进行细化分析,具有可以解调调制信号的功能。在轴承故障中,故障特征频率往往被轴承固有高频所调制,利用希尔伯特变换可以对振动信号有效地进行分析,在现实应用中,显示出了无可比拟的优点。Hilbert变换会使振动信号会产生一个90°相移,可以与原始信号构成一个解析信号,这个解析信号就构成了信号的包络信号[8]。
信号x(t)的希尔伯特变换定义为
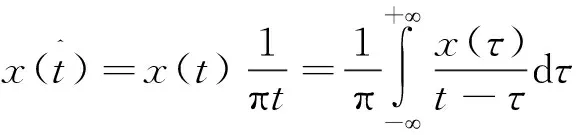
(5)

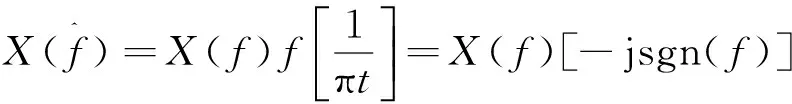
(6)
其中:f表示对信号进行傅里叶变换;sgn(x)为符号函数,X(f)是x(f)在频域中做相位移,在正频域中延迟π/2秒,在负频域则超前π/2秒。Hilbert包络具有解调功能,通过对振动信号进行Hilbert变换,信号的故障特征较为清晰地显现出来,不失为一种理想的处理手段。
2 轴承实测振动信号分析
2.1 轴承故障频率计算
本实验的对象是惠普某型号电机,研究的数据来源于美国Bearing Data Center数据中心的数据,实验的装置如图1所示。
实验中采用JEM SKF公司的6205-2RS深沟球轴承,参数如表1所示。

图1 试验装置图Fig.1 Photo of experimental setup

参 数数 值轴承内径直径/mm25轴承外径直径/mm52轴承厚度/mm15滚动体直径/mm8倾斜直径/mm39接触角/(°)0转速/(r·min-1)1797采样频率/kHz48
滚动轴承在工作过程中,表面如果存在损伤,滚动体经过损伤表面时,就会产生一种交变的激振作用力,滚动表面的损伤形式的不规则性是激振力产生由多种频率成分组成随机振动的原因。轴承相互滚动表面状况的振动机理表明,激振力的频率特征是由轴承滚动表面损伤的形态和轴的旋转速度共同决定,激振力的传递特性则由轴承和外壳体的支撑刚性所决定,上述两种特性共同决定着整个轴承振动系统的最终频率[9]。
按照该型号轴承的基本参数,不同损伤类型的轴承故障频率理论计算结果如下所示[10]:
1)内滚道缺陷时特征频率为
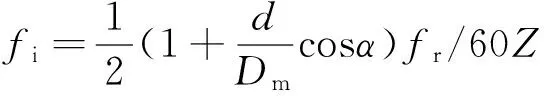
(7)
2)外滚道缺陷时特征频率为
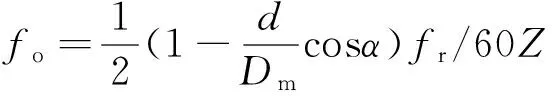
(8)
3)滚动体缺陷时特征频率为
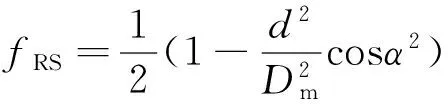
(9)
4)保持架碰外圈时特征频率为
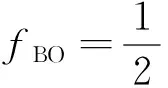
(10)
5)保持架碰内圈时特征频率为
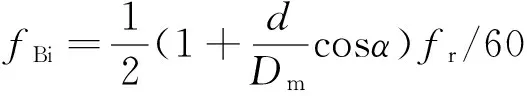
(11)
其中:fr为轴承转速;Dm为轴承滚道节径,即内外滚道的平均值;d为滚动体直径;α为轴承的压力角,也称为接触角;Z为滚动体个数。
本型号轴承滚动体个数为9,代入轴承基本参数通过轴承的故障频率公式计算可得出各部位故障频率为表2所示。
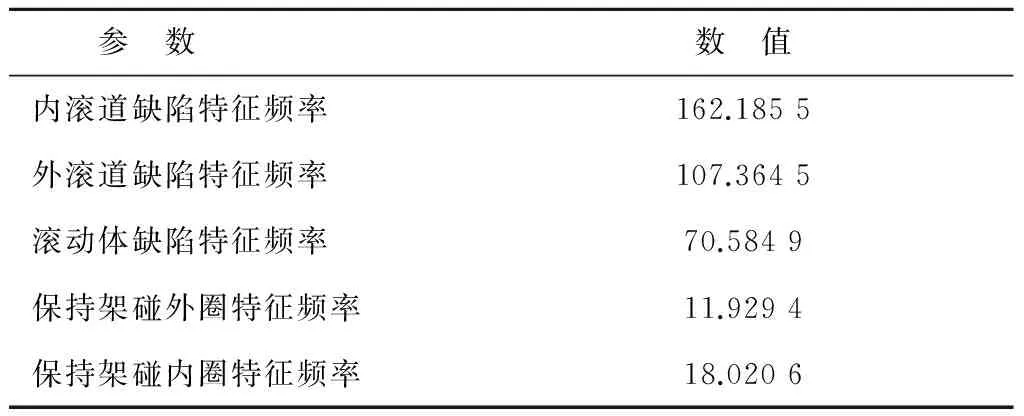
表2 惠普电机轴承故障特征频率表
2.2 轴承振动信号时频域分析
实验记录了两组信号,其中第一组长度达243 938个,采样频率为48 kHz。将采集到的振动信号经过放大电路、滤波器处理然后被转变为数字信号传递到计算机中,如图2、图3所示,单从采集到的轴承振动信号时域、频域图上很难得知其运行状况是否正常。
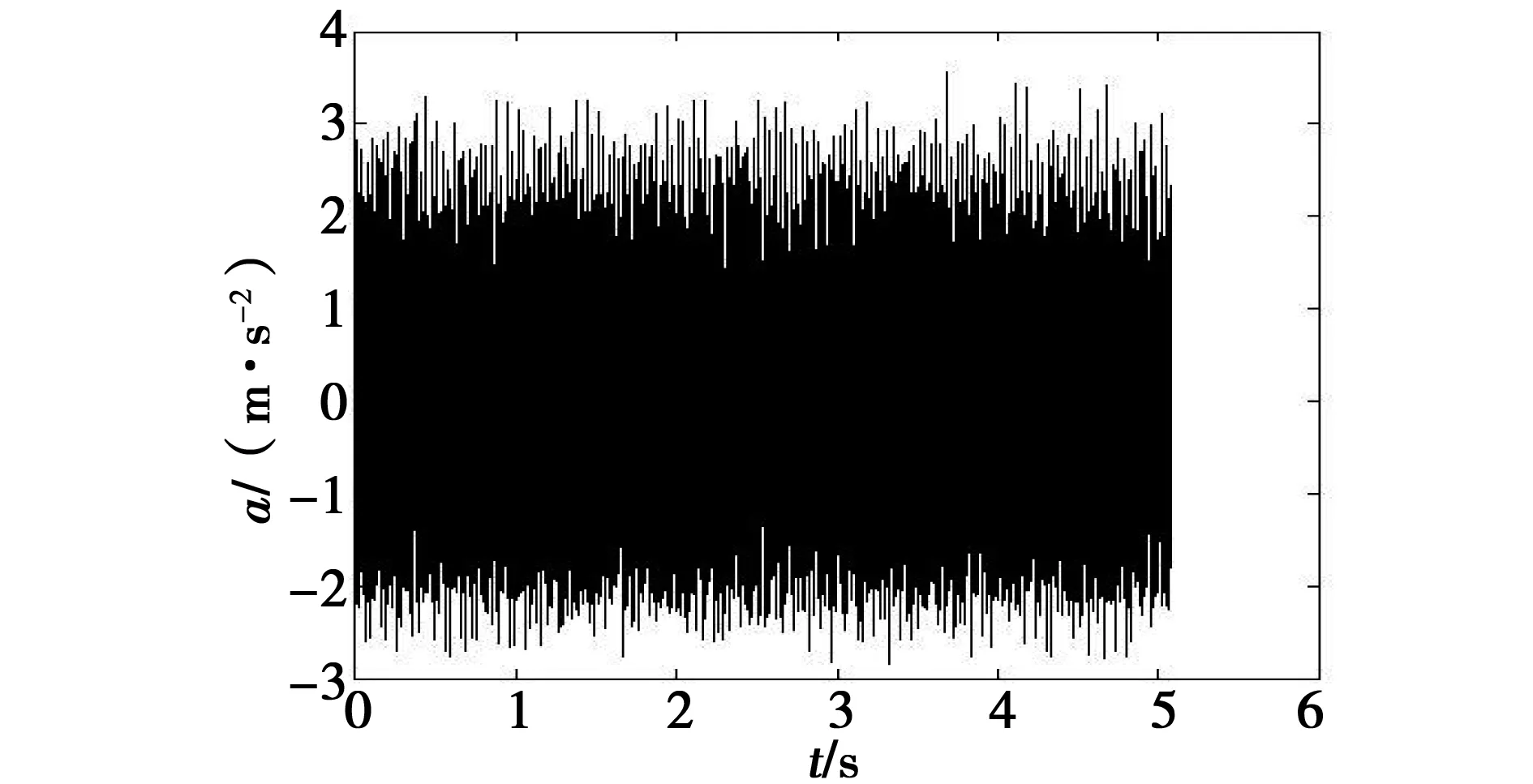
图2 第一组信号时域图Fig.2 Figure of the first set of signals in the time domain
对采集到的轴承振动信号进行本文提出的Thselect函数降噪,在这里小波基函数采用db5,分解了5层,分解后的信号时域图和频域图如图4、图5所示。
从频域图可以看出,经过本文提出的降噪方法处理后,有效地消除了高频干扰。对经过降噪后的信号再用小波包进行三层分解,以第一频段重构波形,并进行希尔伯特解调和细化谱分析,如图6所示。
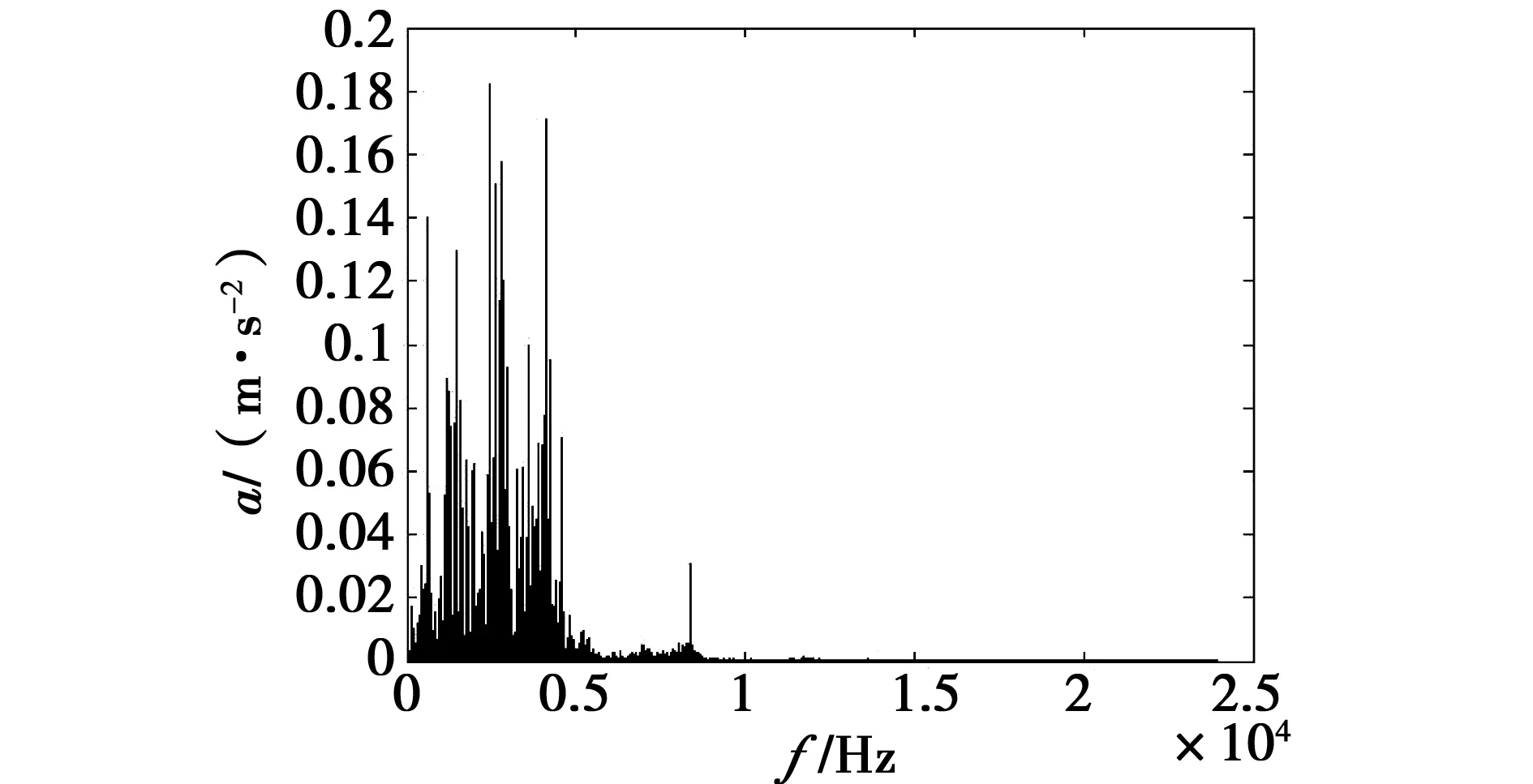
图3 第一组信号频域图Fig.3 Figure of the first set of signals in the frequency domain
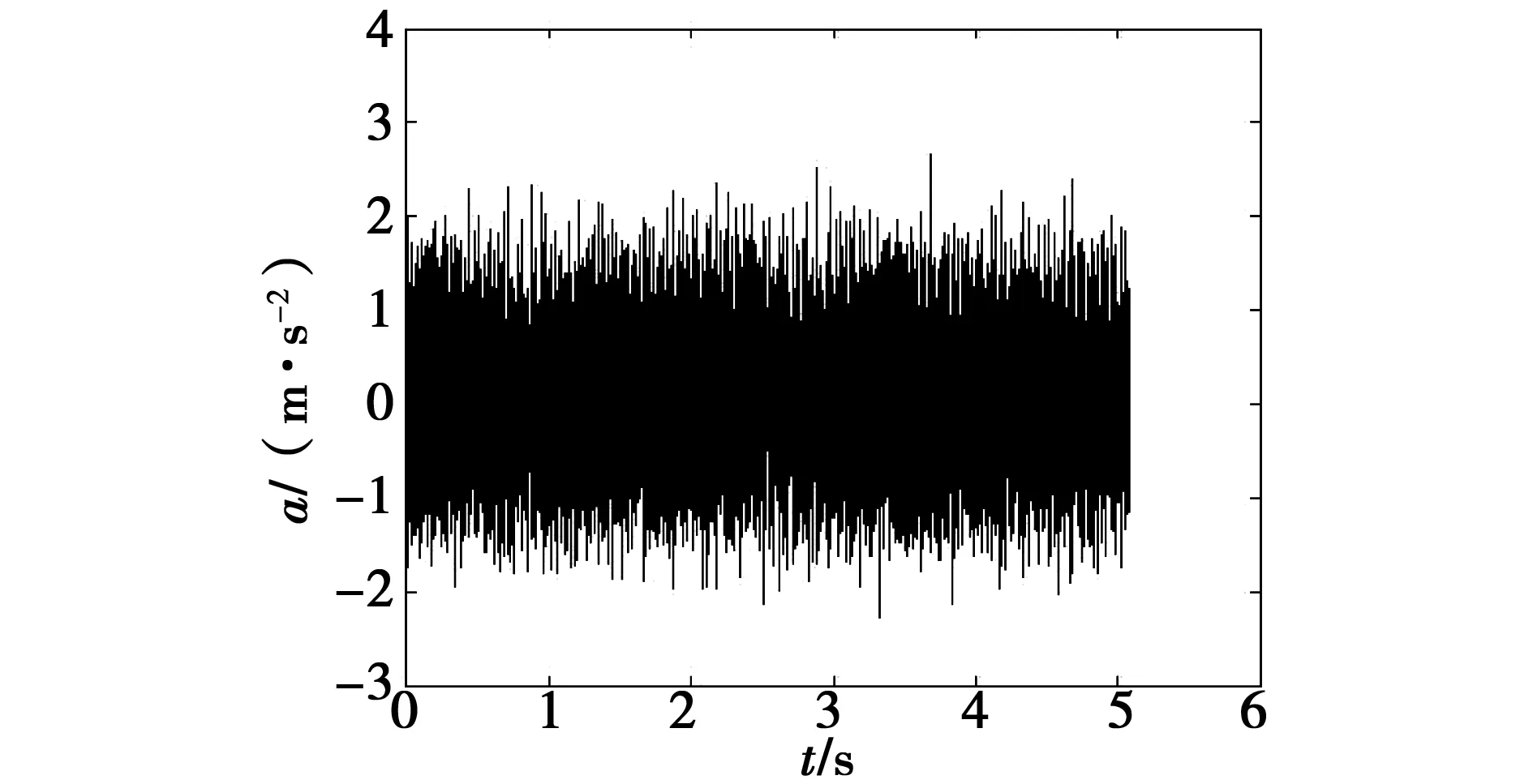
图4 降噪后第一组信号时域图Fig.4 Figure of the first set of signals in the time domain after denoising
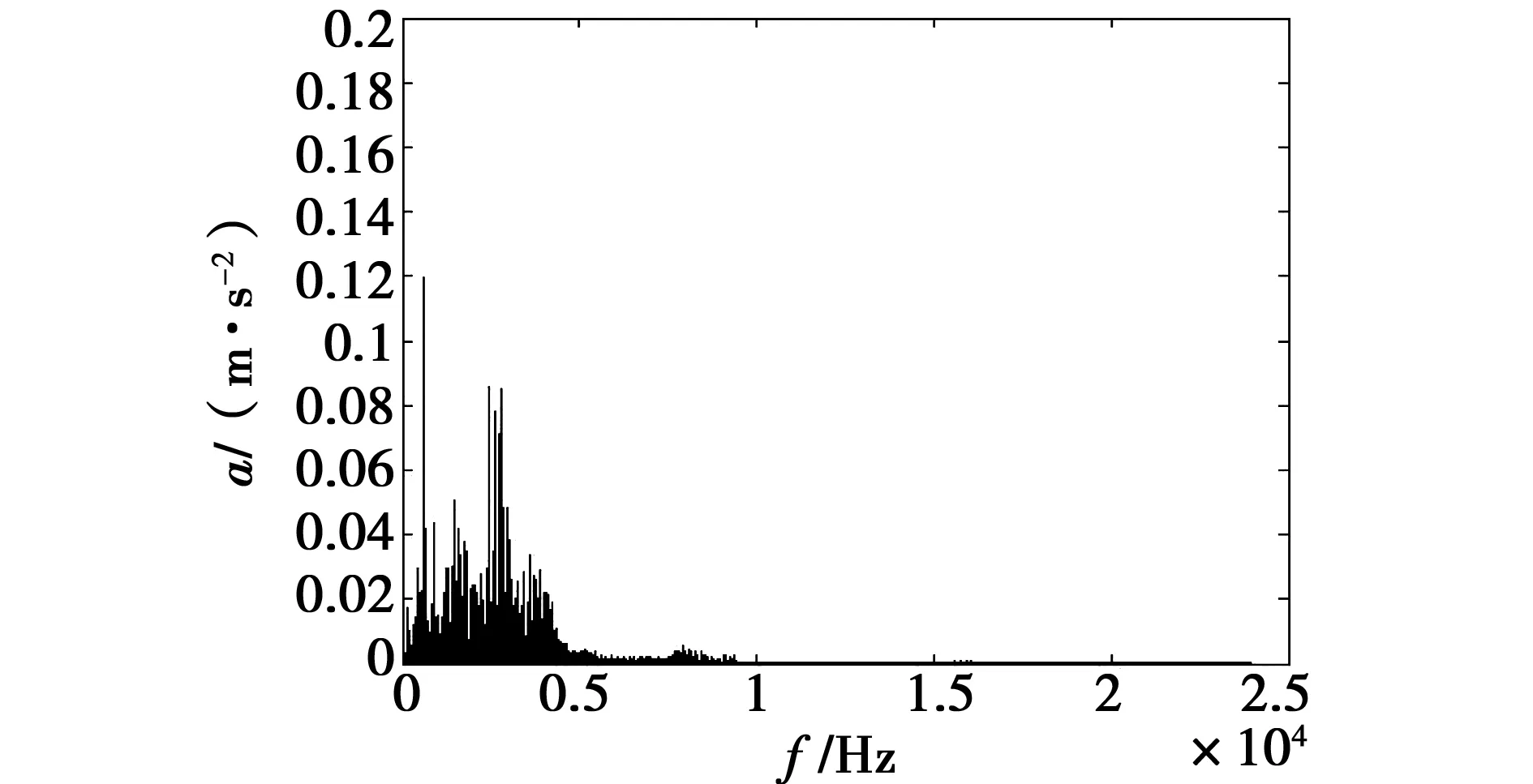
图5 降噪后第一组信号频域图Fig.5 Figure of the first set of signals in the frequency domain after denoising
可以看出,高频干扰得到进一步消除,故障特征信息比较清楚地展现出来。
主流信号处理方法一般是小波分析,为了体现本方法相比小波处理的优越性,将只经过小波处理后的振动信号与经过小波及希尔伯特变换处理后的振动信号频域图做一对比,分别如图7、图8所示。
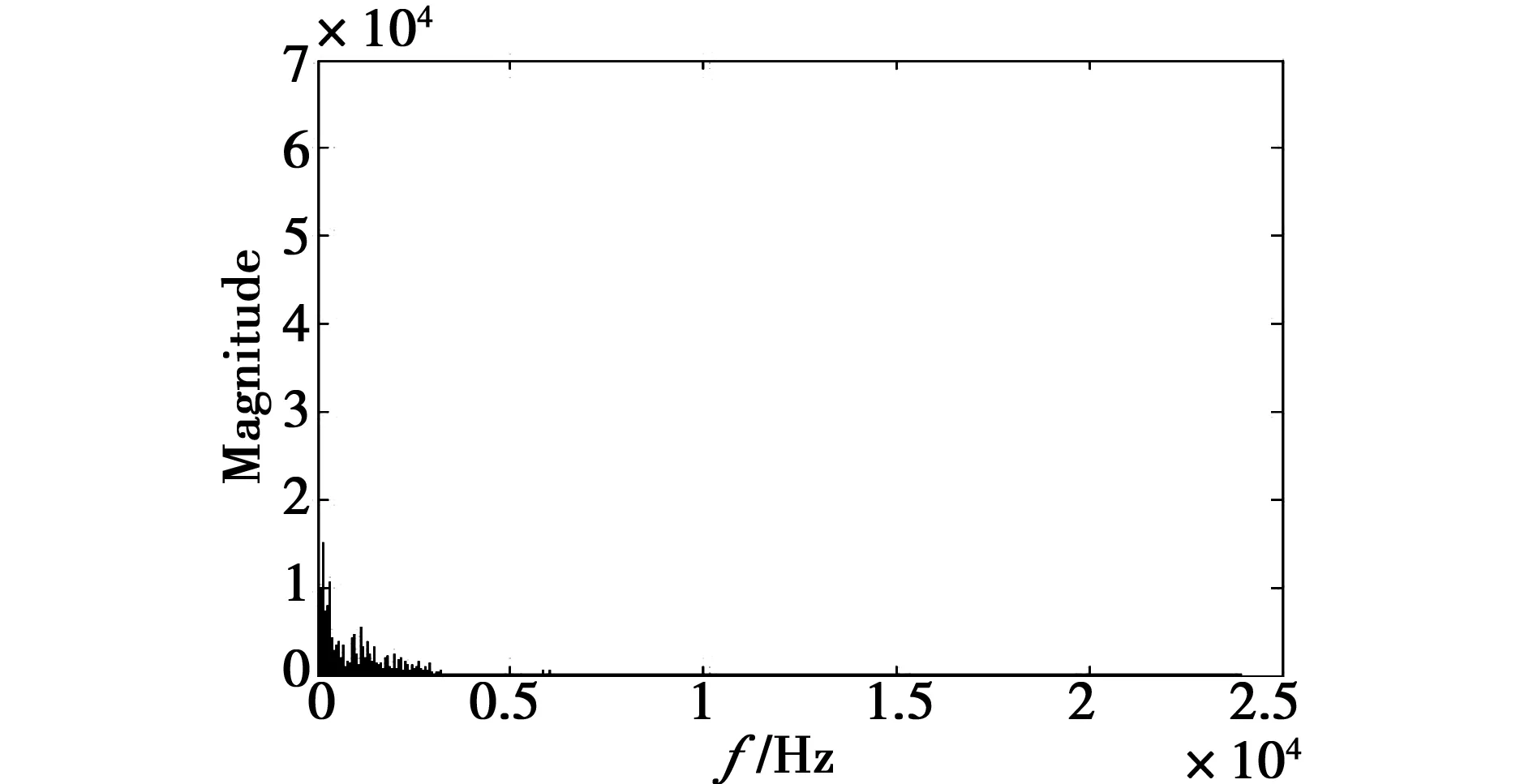
图6 第一组信号希尔伯特解调细化谱图Fig.6 Figure of the first set of signals hilbert demodulation refinement spectrum
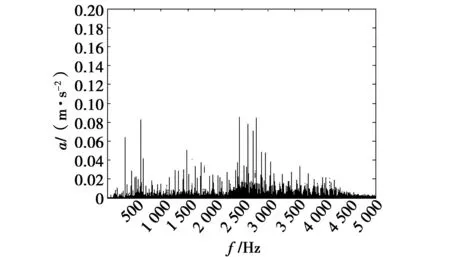
图7 小波处理的第一组信号频域图Fig.7 Figure of the first set of signals in the frequency domain after wavelet processing
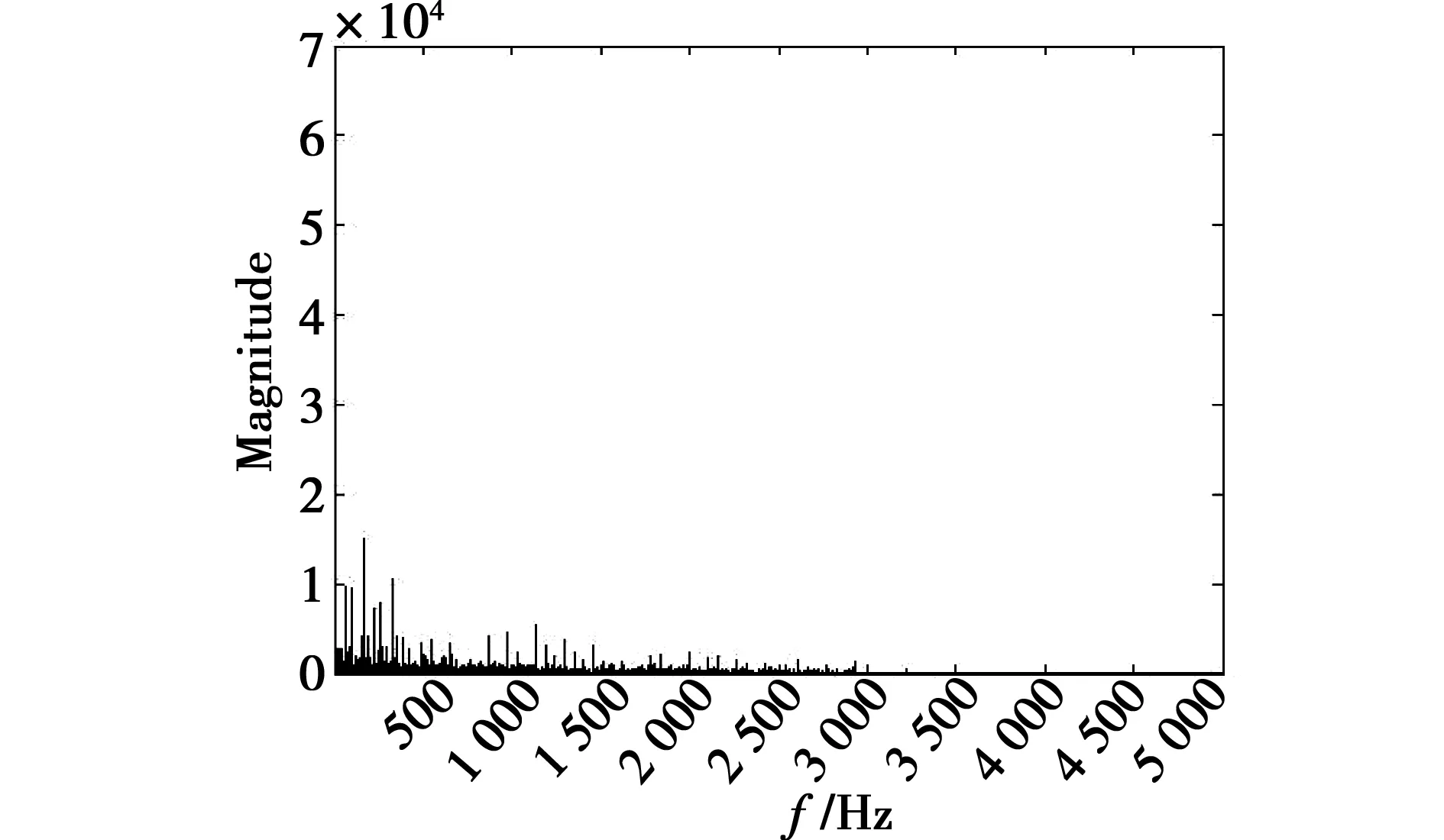
图8 本方法处理后第一组信号频域图Fig.8 Figure of the first set of signals in the frequency domain after this method processing
可以看出,只经过小波处理,信号高频干扰没有被有效抑制,故障特征不明显,而利用本方法有效地去除高频干扰,使得故障特征更加突出,可以看到在大概200 Hz附近的幅值相比较高。
对经过处理后的信号取其0~500 Hz范围频率部分,如图9所示。
从图9细化谱中可以清晰地看出频率162 Hz处幅值最为突出,相比较计算所得的内圈故障频率162.185 5 Hz,误差不大。从而就能判断出该轴承的内圈部位可能出现了故障。
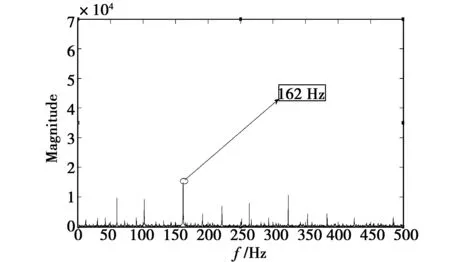
图9 本方法处理后第一组信号频域图(0~500 Hz)Fig.9 Figure of the first set of signals in the frequency domain between 0~500 Hz after this method processing
实验又记录了另一组电机轴承振动信号,长度为485 643个,采样频率不变,其时域和频域如图10、图11所示。
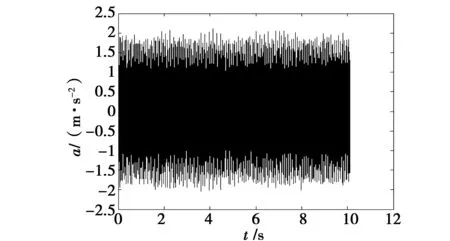
图10 第二组信号时域图Fig.10 Figure of the second set of signals in the time domain
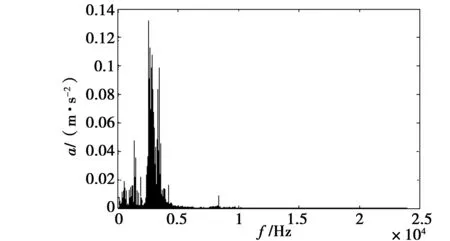
图11 第二组信号频域图Fig.11 Figure of the second set of signals in the frequency domain
可以看出,从原始信号时域图根本看不出来故障特征,高频分量严重干扰了低频故障特征的提取,利用小波降噪后,结果如图12、图13所示。
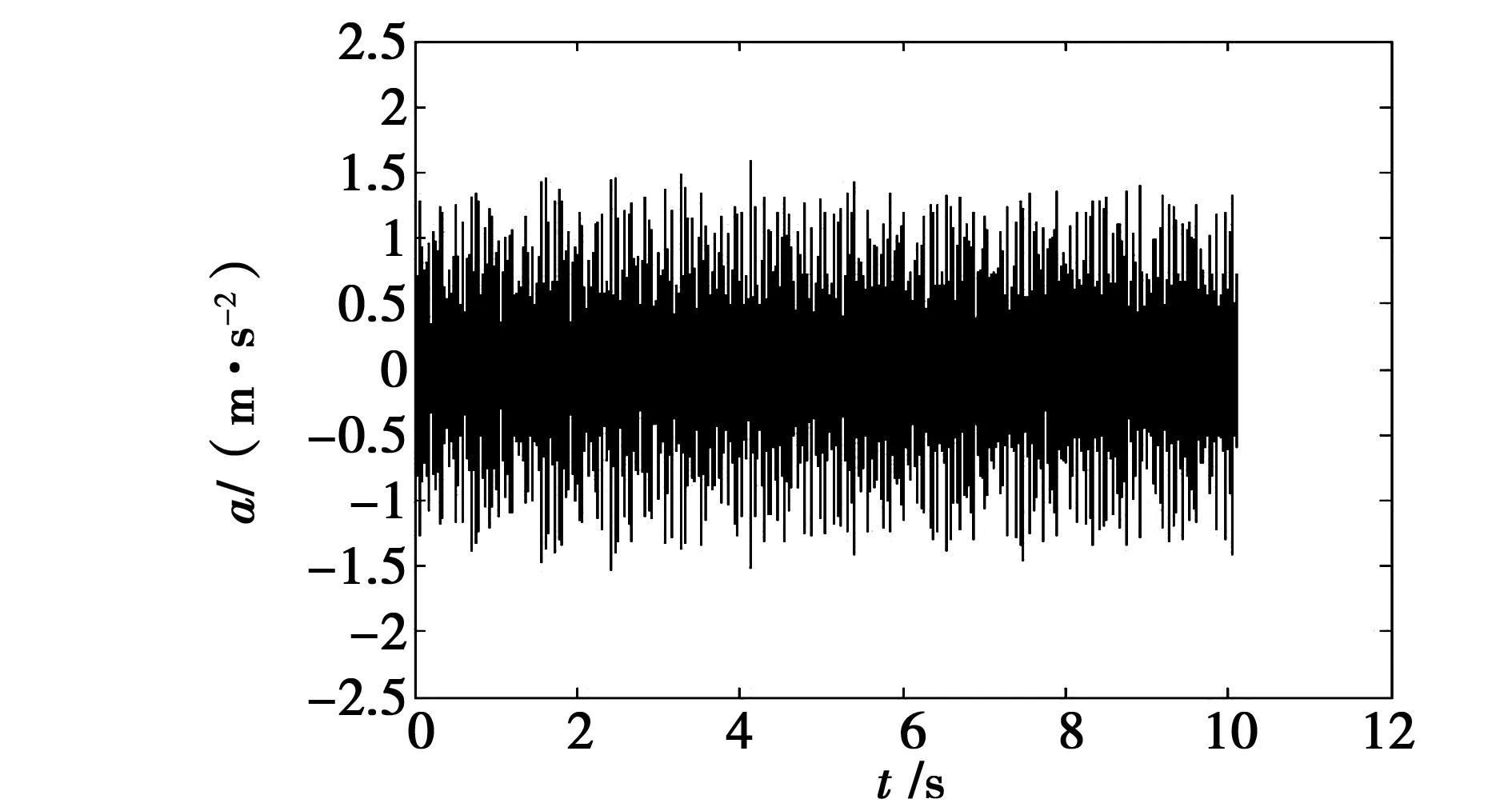
图12 降噪后第二组信号时域图Fig.12 Figure of the second set of signals in the time domain after denoising
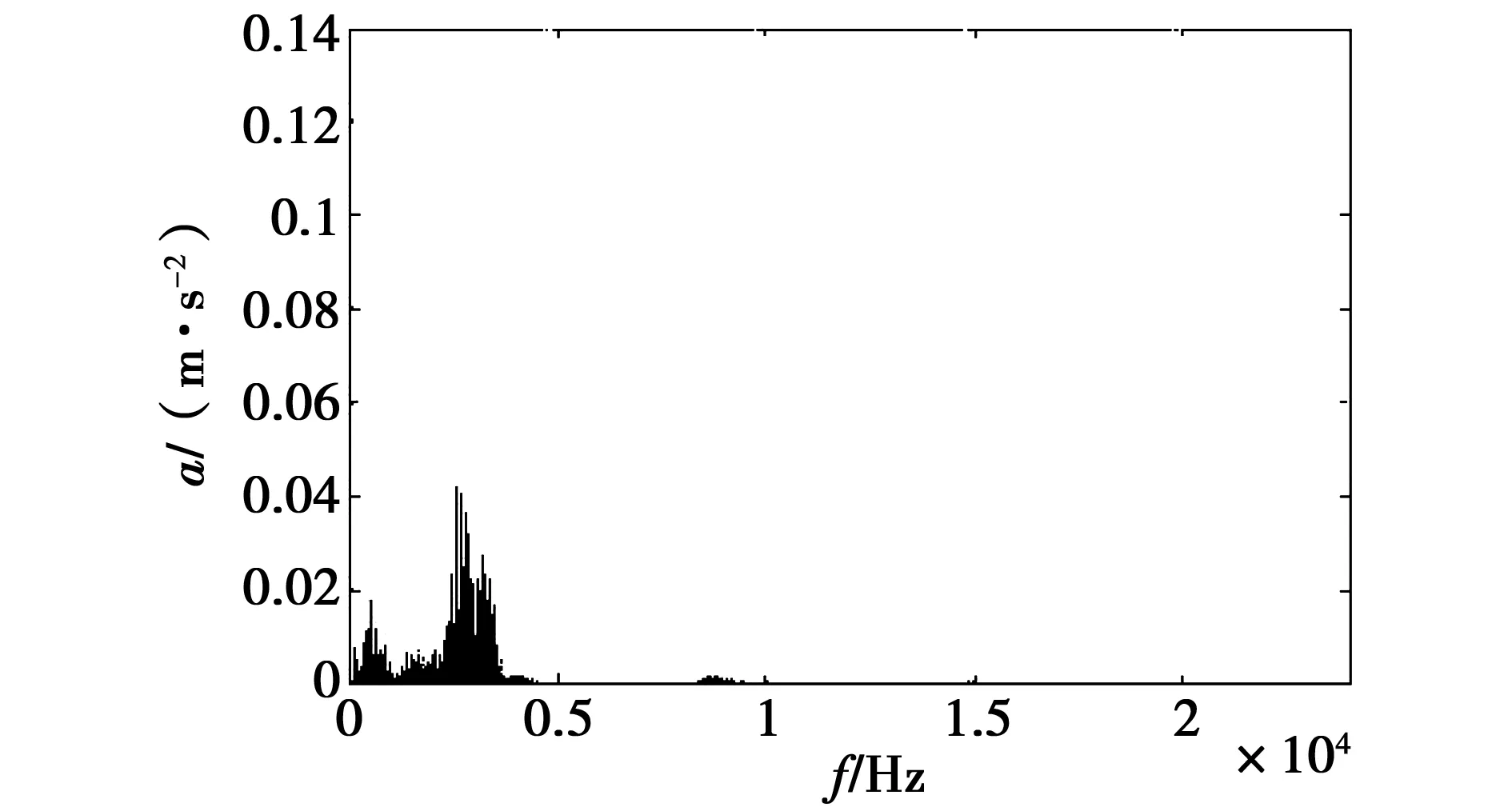
图13 降噪后第二组信号频域图Fig.13 Figure of the second set of signals in the frequency domain after denoising
经过降噪后高频干扰被抑制,低频特性展现出来,对经过降噪后的信号再用小波包进行三层分解,以第一频段重构波形,并进行希尔伯特解调和细化谱分析,如图14所示。
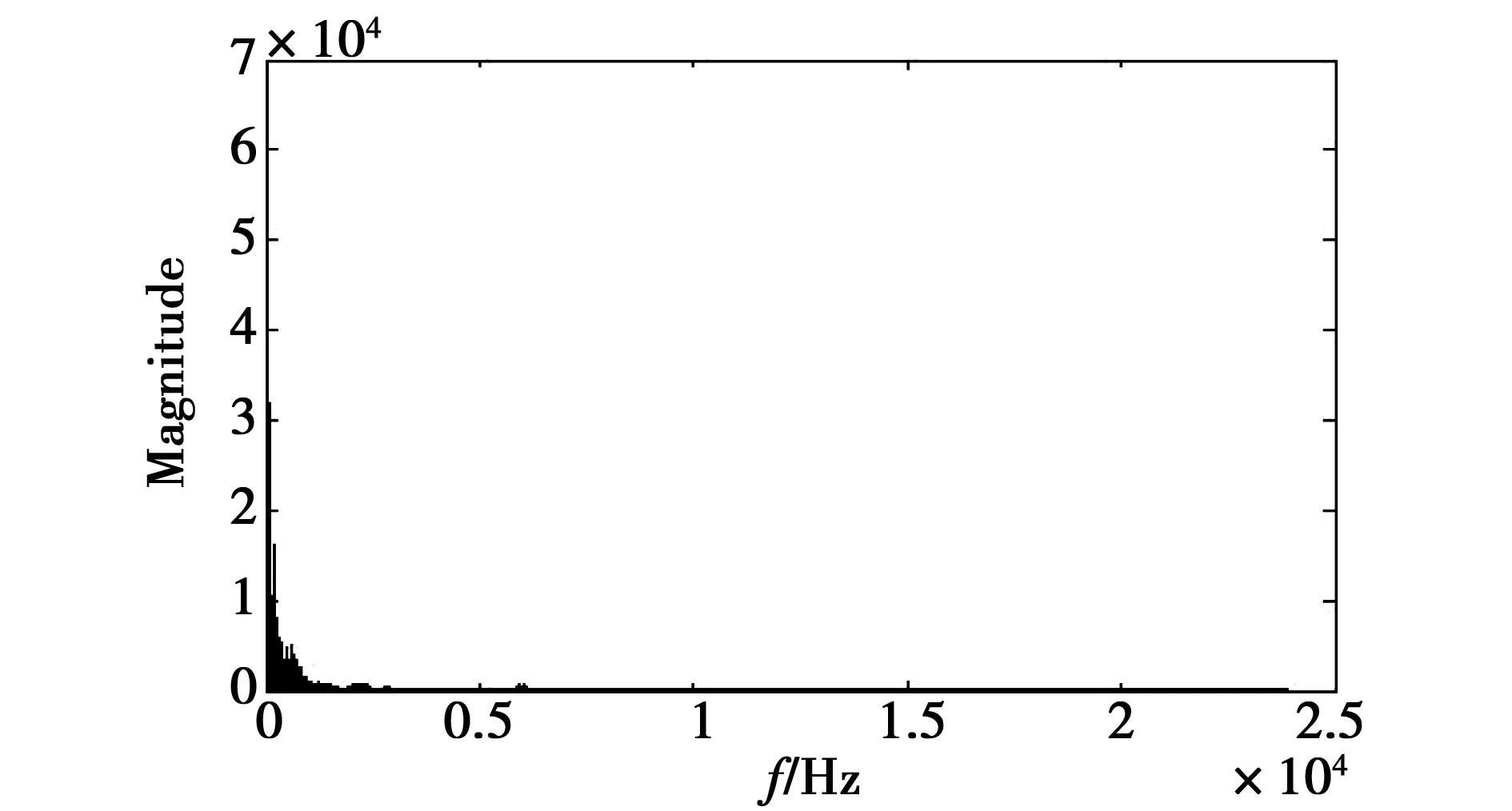
图14 第二组信号希尔伯特变换解调细化谱图Fig.14 Figure of the second set of signals hilbert demodulation refinement spectrum
从图中可以看出,高频干扰进一步得到了消除。
对比只经过小波处理后的信号频域图,可以看出小波及希尔伯特变换处理后的效果比只经过小波处理后的故障特征更突出,如图15、图16所示。
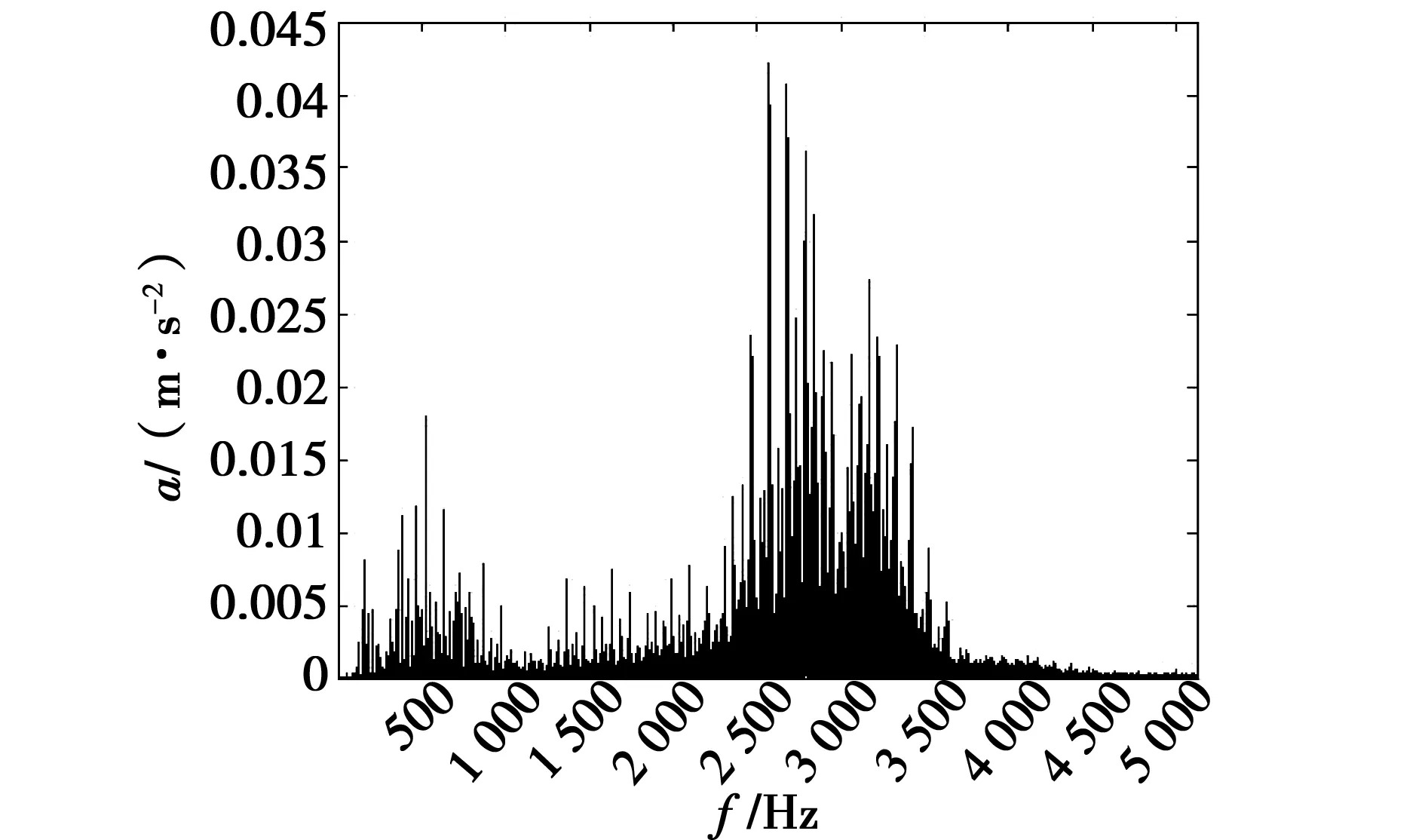
图15 小波处理的第二组信号频域图Fig.15 Figure of the second set of signals in the frequency domain after wavelet processing
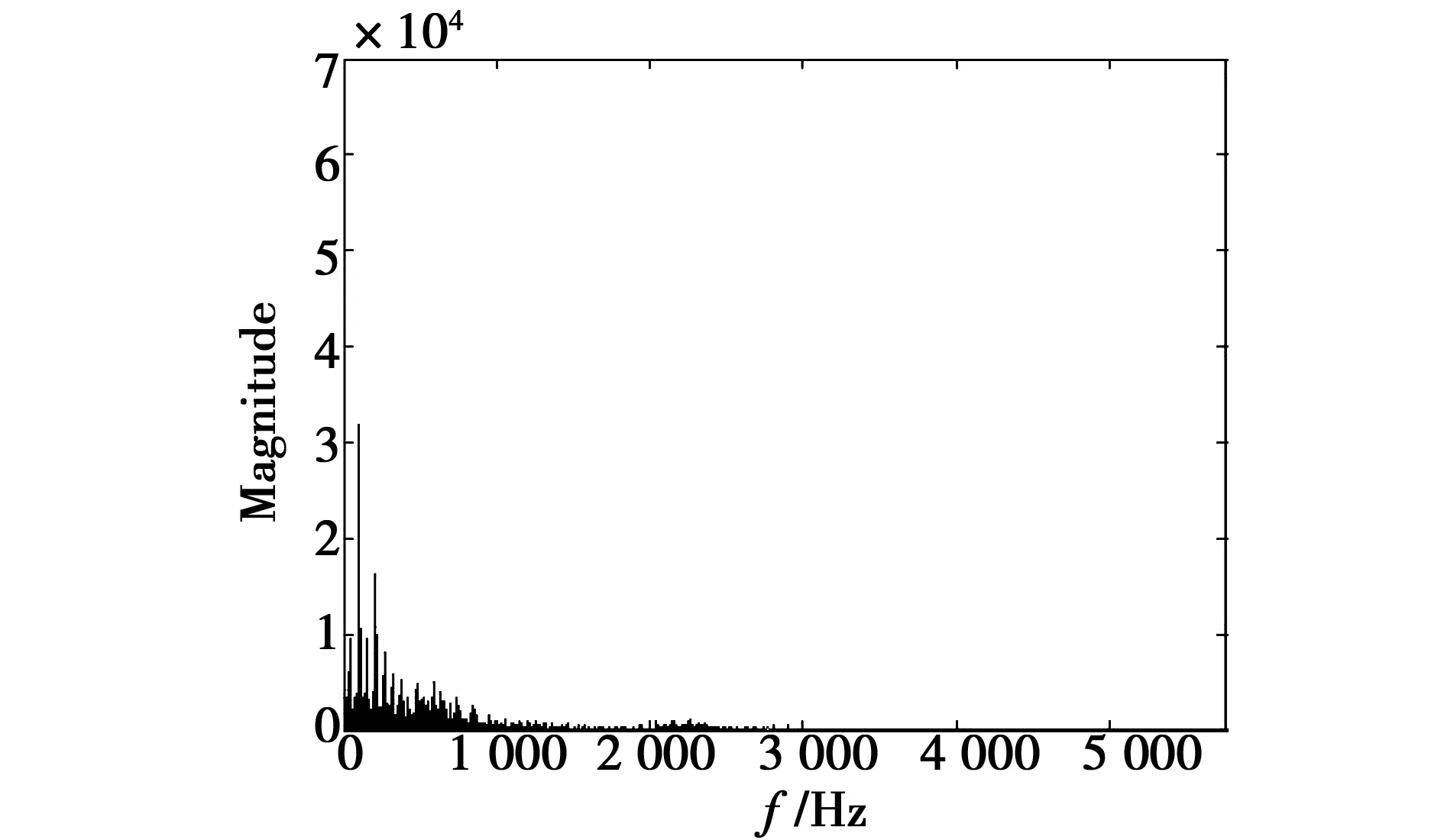
图16 本方法处理后的第二组信号频域图Fig.16 Figure of the second set of signals in the frequency domain between 0~500 Hz after this method processing
提取经过小波及希尔伯特变换处理后信号的0~500 Hz范围频率部分,如图17所示。
由图17可以看出,在107 Hz和214 Hz处,幅值最大,对比计算出来的故障特征频率表,与外圈频率107.364 5 Hz及其二倍频214.729 0 Hz相差不大,所以电机轴承的外圈部位可能出现了故障,与实际结果一致。
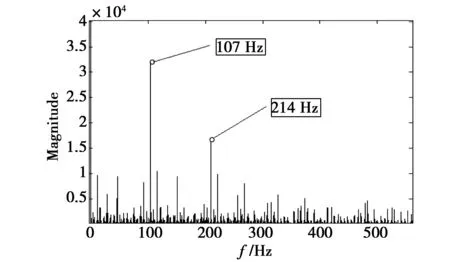
图17 本方法处理后第二组信号频域图(0~500 Hz)Fig.17 Figure of the second set of signals in the frequency domain between 0~500 Hz after this method processing
3 结 论
机械振动故障诊断是信号处理应用范畴中的一大难点,当前有多种分析处理手段,但各有所弊,如何针对所要研究分析的对象来选用有效的信号处理方法尤为重要。本文利用小波降噪中的Thselect函数进行降噪,为每个小波分解层系数设置自适应阈值,从而有效消除了高频信号的影响,再利用希尔伯特变换可以对信号解调和细化谱分析的的功能,对降噪后的振动数据进行希尔伯特变换,提取出了电机轴承的低频故障特征,通过与主流方法进行分析比较,更具有优势,准确检测出轴承故障类型,具有一定的实际应用价值。
[1] 安国庆, 秦程, 郭立炜, 等. 峭度滤波器用于电机轴承早期故障特征提取[J].电机与控制学报, 2014, 18(6): 55-60. AN Guoqing, QIN Cheng, GUO Liwei, et al. Kurtosis filter in feature extraction for incipient motor bearing fault diagnosis[J]. Electric Machines and Control, 2014, 18(6): 55-60.
[2] 唐贵基, 王晓龙. 自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报, 2015, 35(6): 1436-1444. TANG Guiji, WANG Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis of bearing[J]. Proceedings of the CSEE, 2015, 35(6): 1436-1444.
[3] 张雄希, 刘振兴. 共振解调与小波降噪在电机故障诊断中的应用[J]. 电机与控制学报, 2010,14(6):66-70. ZHANG Xiongxi, LIU Zhenxing. Application of resonance demodulation and wavelet denosing in fault diagnosis of induction motors[J]. Electric Machines and Control, 2010, 14(6): 66-70.
[4] KUMAR H S. Wavelet transform for bearing condition monitoring and fault diagnosis[J]. International Journal of COMADEM, 2014, 17(1): 9-23.
[5] 丁锋, 何正嘉, 张新运. 小波包分析在滚动轴承信号消噪处理中的应用[J].西安工业学院学报, 2006, 26(1): 8-12. DING Feng, HE Zhengjia, ZHANG Xinyun. Application of wavelet packet analysis in signal denoise of rolling bearing[J]. Journal of Xi’an Institute of Technology, 2006, 26(1): 8-12.
[6] 张德丰.详解MATLAB数字信号处理[M].北京:电子工业出版社,2010:325-329.
[7] ROEMER M J, K Acprzynski G J. Advanced diagnostic and prognostics for gas turbine engine risk assessment[C]//Aero space Conference Proceedings, USA, IEEE. 2000:345-353.
[8] BACHA Khmais. An improved combination of Hilbert and Park transforms for fault detection and identification in three-phase induction motors[J]. International Journal of Electrical Power and Energy System, 2012:1006-1016.
[9] LI Bing, ZHANG Peilin, LIU Dongsheng. Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transform and two-dimensional non-negative matrix factorization[J]. Journal of Sound and Vibration, 2011, 33(10): 2388-2399.
[10] 时献江, 王桂荣, 司俊山, 等.机械故障诊断及典型案例解析[M].北京:化学工业出版社,2013:102-116.
(编辑:刘琳琳)
Application of wavelet denoising and Hilbert transform in fault diagnosis of motor bearing
DING Feng, QIN Feng-wei
(Department of Mechanical and Electronic Engineering, Xi′an Technological University, Xi′an 710021, China)
Vibration signal denoising and fault feature extraction is the key focus of mechanical fault diagnosis, in order to effectively eliminate the impact of high frequency vibration signals, and fully extract the low frequency fault characteristics of motor bearings.A method that combined Wavelet denoising with Hilbert transform was put forward to deal with and analyze the vibration signals measured from motor bearing to extract fault feature. Firstly, the wavelet denoising was applied to rotary mechanical bearing data to suppress the noise interference. Then, Hilbert transform was used to deal with the denoised signal to extract the fault feature. On the basis of bearing vibration data acquisition on site and by the signal processing, the ideal effect of diagnosis can be achieved. Thus it is known that the method can process fault characteristic information by the bearing vibration signal, and bearing fault analysis and diagnosis is implemented effectively.
bearings; vibration signal; the wavelet denoising; Hilbert transform
2015-12-15
国家自然科学基金(51275374);国防科技重点实验室开放基金
丁 锋(1968—),男,博士,教授,博士生导师,研究方向为设备状态监测及维护、可靠性评估与优化设计等; 秦峰伟(1988—),男,硕士,研究方向为设备状态监测及故障诊断。
丁 锋
10.15938/j.emc.2017.06.012
TH 111.3
A
1007-449X(2017)06-0089-07

