关于双曲拱桥有限元建模方法研究

陈庚（福州轨道交通设计院有限公司，福州350009）

关于双曲拱桥有限元建模方法研究

陈庚
（福州轨道交通设计院有限公司，福州350009）

本文采用M ID A S/C ivil有限元软件对两座双曲拱桥进行建模，通过实桥试验结果进行对比验证，分析本文提出的建模方法的准确性，分析结果表明，采用提出的建模方法计算分析得到的结果与实桥试验测试结果整体趋势上保持一致，分析计算精度较高，可适用于双曲拱桥的静载试验结果分析。

双曲拱桥建模方法纵梁截面实桥试验

0 引言

双曲拱桥作为传统的民族建筑产物，其主拱圈主要由拱肋和拱波组成，由于其合理的受力构造组成，结合具有良好抗压性能的混凝土材料，在早期的桥梁建筑中得到广泛应用。但是由于当时的施工技术都比较不成熟，且重载交通的日益增多，许多处于服役状态的双曲拱桥均存在一定的安全隐患，所以对于此类桥梁要按照现行规范荷载进行相应的设计验算[1]以了解桥梁的受力状态，存在安全隐患的桥梁要进行必要的加固处理[2-3]，严重的甚至要重建。

目前对于双曲拱桥受力验算主要采用有限元分析方法，其空间模型的建立采用的建模方法主要有实体单元体系[4-5]和空间杆梁体系，实体单元建模方法是以实体单元基本还原实桥的整体结构，能较为精确地计算出各部位的受力特性，其计算精度随着实体单元的划分精度的提高而提高，但是随之而来的是不断增大的工作量，在后处理上也将存在繁琐的调整工作，不适用于桥梁静动载分析验算，所以在实际的静动载分析中，常用采用空间杆系的方法建模。

空间杆系建模方法在建模过程中主要解决的问题有：等效截面刚度，其中包括拱肋和横向联系的截面刚度模拟，目的是能如实反映桥梁结构在荷载作用下的受力情况，在相同位置作用相同荷载时，模型的结构挠度和应力分布上能与实桥基本吻合；梁格间距的设置，若横向虚拟构件的布置过于稀疏，将会导致应力分布的不连续性，降低分析结果的精确性，若布置过于密集，就会使梁格的受力特性接近于分隔式上部结构，也会造成分析结果的不准确性。

施工工艺对于结构的整体受力特性有着根本性的影响，双曲拱桥的施工正常是将拱肋分段、拱波分块分层进行预制吊装，安装到位后在上面浇筑一层拱波混凝土，使其成为一个整体，最后才进行拱顶填料的填充。在结构的整体受力上，纵向拱肋主要承受纵向弯矩和轴向压力，横向拱波主要承受横向弯矩和拉压力，且拱波在结构形式上属于壳结构[6]，所以要根据余能等效原则[7]对截面进行处理。

在双曲拱桥杆系模型建模过程中，若仅考虑拱肋和拱波作为纵梁截面进行分析时，桥梁变形过大，结构整体刚度偏小，导致分析结果失真。文献[8]在探索空腹式双曲拱桥的建模过程中，提出的建模方法就是将现浇混凝土部分也考虑到纵梁截面，但是得到的分析结果与试验结果对比发现，分析结果得到的结构主要截面变形均略大于试验结果，说明设计的纵梁截面刚度偏小，这主要是由于没有考虑拱上结构的联合作用[9]导致的。

故在上述研究的基础上，本文针对空腹式双曲拱桥和实腹式双曲拱桥，提出两种关于纵梁截面的建模方法。

1 双曲拱桥建模方法

1.1 空腹式双曲拱桥

对于空腹式双曲拱桥，主要通过在主拱圈上方建设立柱支撑起整个桥面，其主拱圈的断面图如图1（a）所示，单个纵梁截面如图1（b）所示，故在建模过程中，可采用如图1（c）所示截面作为纵梁分析截面。

1.2 实腹式双曲拱桥

实腹式双曲拱桥，拱上填料通常采用片石混凝土或贫混凝土，尤其在拱脚处的拱上填料高度大、重量大，大大增加了桥身自重，与此同时，拱上填料也增大了桥梁的整体结构刚度，其横断面图如图2（a）所示，若根据文献[8]的建模方法，不考虑拱上填料的刚度，得到的纵梁刚度仍会小于实桥的刚度，造成分析的不准确性，所以本文在其基础上，也将拱上填料的刚度进行模拟，根据填料类型和密实程度的不同，采用的材料弹性模量取值范围为7× 103~9×103MPa，容重的取值范围为15~17kN/m3，考虑到桥面系的现浇混凝土增强了填料的整体刚度和横向联系，将纵向和横向联系均采用弹性模量取值范围为2.8×104~ 3.0×104MPa的零容重虚拟材料进行模拟，而主拱圈拱肋的纵梁截面，采用与文献[8]一样的纵梁截面形式进行建模。

图1 空腹式双曲拱桥拱肋纵梁截面设计

图2 实腹式双曲拱桥拱肋纵梁截面设计

2 建模方法精度验证

本文采用上述建模方法和MIDAS/Civil有限元软件分别建立一座空腹式双曲拱桥和一座实腹式双曲拱桥，并与实桥的静载试验实际试验结果进行对比，分析本文提出的双曲拱桥建模方法的精确度。

2.1 空腹式双曲拱桥

双曲拱桥A为一座空腹式钢筋混凝土双曲拱桥，净跨径L0=55m，矢跨比f0/L0=1/8。拱圈横向由五片拱圈组成，每片拱圈横向间距为1.55m。桥梁总宽度6.70m= 0.65m（栏杆及人行道）+5.40m（机动车道）+0.65m（栏杆及人行道）。具体的纵断面图和横断面图，以及通过Midas/ Civil有限元软件建立的模型如图3所示。

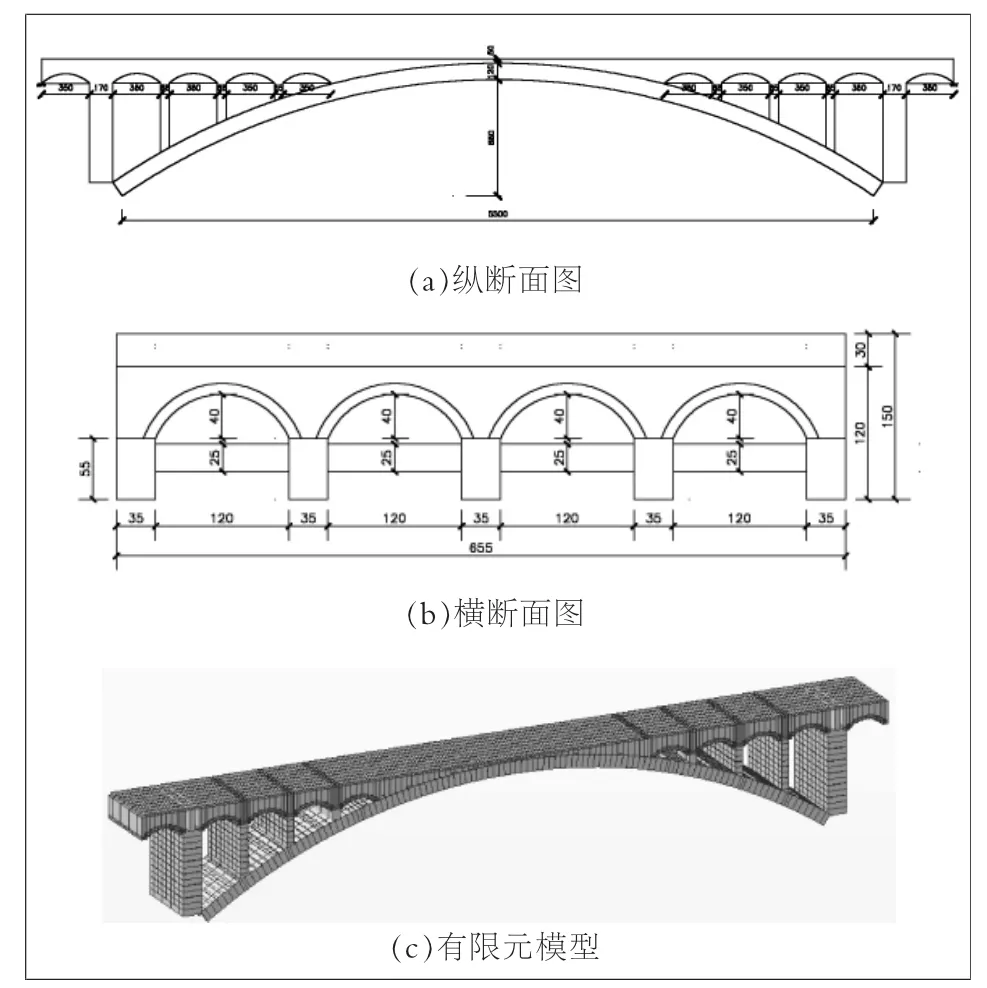
图3 双曲拱桥A截面图和有限元模型

挠度测点布置在测试跨的L/4、L/2和3L/4截面，每个截面布置上游和下游2个挠度测点，可以了解在偏载作用下，两侧挠度的差别，进一步验证有限元模型计算分析的精确度，采用百分表进行测量。全桥共布置6个挠度测点。

应变测试设置3个应变测试截面，分别对应拱顶截面、L/4截面和拱脚截面。全桥共布置15个应变测点。

全桥测试包括2个工况，分别为工况1：拱顶截面最大正弯矩工况（偏载）；工况2：拱脚截面最大负弯矩工况（偏载）。加载车规格与布载情况如图4所示，空间模型计算结果与试验结果对比如表1~2所示。

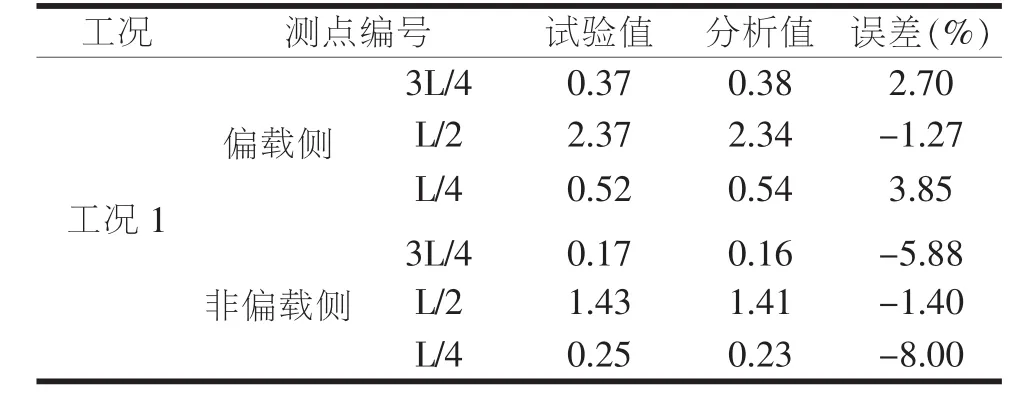
表1 模型分析挠度值与试验值对比（mm）

表2 模型分析应变值与试验值对比

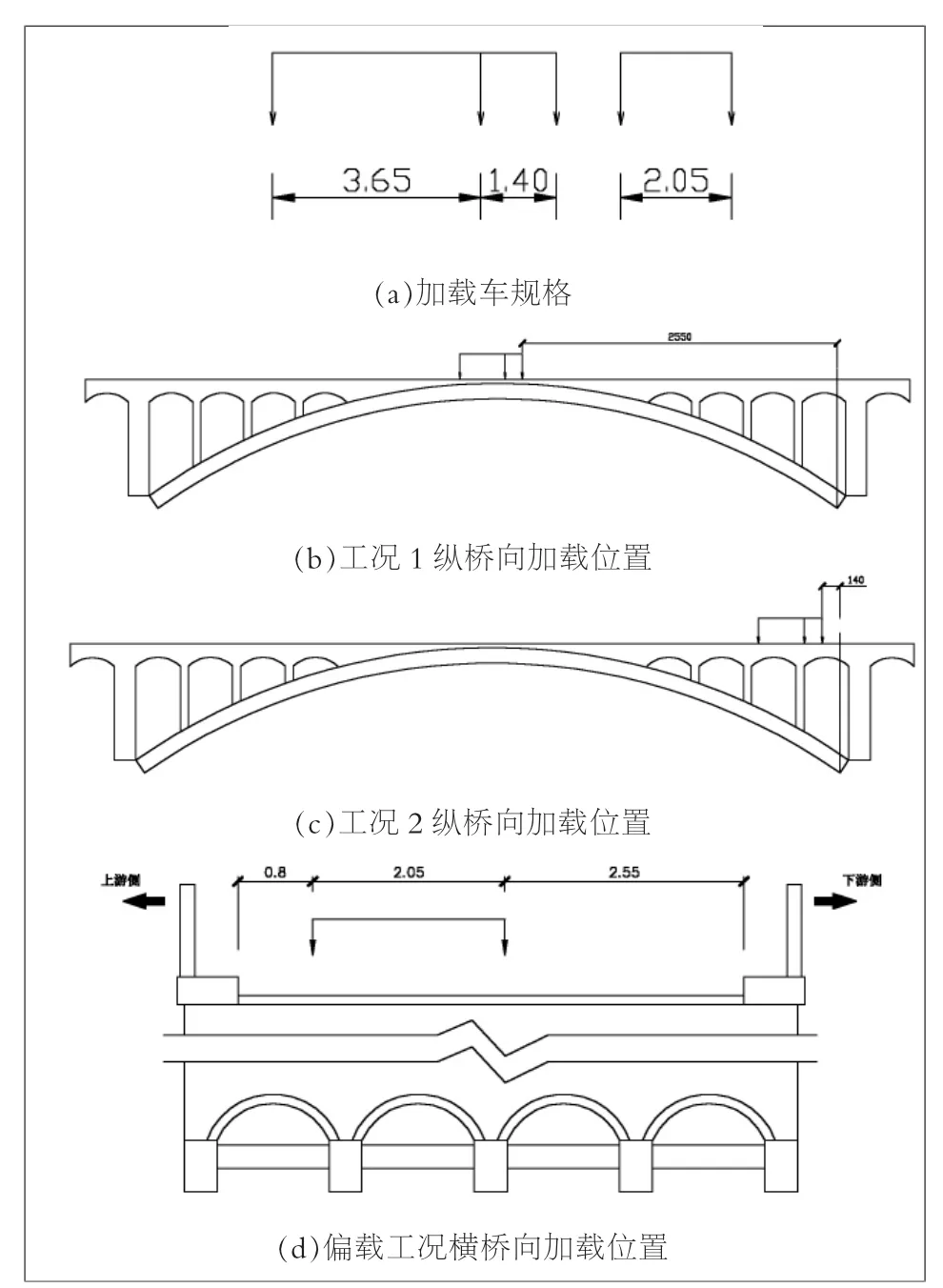
图4 试验工况布载情况

从分析和测试结果的对比可看出，在计算桥梁变形上，二者之间的误差均控制在8%以内，而在关键截面的应变计算上，二者的误差均控制在15%内。

2.2 实腹式双曲拱桥

双曲拱桥B为一座两跨等跨实腹式双曲拱桥，桥梁全长70.0m，桥梁宽度7.0m，车行道净宽度为6.3m，双曲拱拱圈净跨径为23.0m，净矢高为5.667m，横向由6片砼拱肋、砌石拱波、拱板及混凝土横系梁组成，单片拱肋宽0.30m，拱肋净间距为1.00m，具体的纵断面图和横断面图，以及通过Midas Civil有限元软件建立的模型如图5所示。

挠度测点布置在测试跨的L/2和L/4截面，每个截面布置6个挠度测点，采用百分表进行观测，分析在偏载作用下挠度在横桥向的变化规律。全桥共布置12个挠度测点。

通过应变测试值与理论计算值的比较，判断桥梁整体刚度与截面承载刚度是否满足使用要求。拱肋应变测试采用电阻应变片以及静态数据采集系统，测试孔设置3个应变测试截面，分别对应拱脚、1/4孔截面和拱顶，全桥累计布置18个应变测点。

全桥测试包括2个工况，分别为工况1：拱顶截面最大正弯矩工况（偏载）；工况2：拱脚截面最大负弯矩工况（偏载）。加载车规格与布载情况如图6所示，空间模型计算结果与试验结果对比如表3~4所示。

图5 双曲拱桥B截面图和有限元模型

图6 试验工况布载情况

实腹式双曲拱桥模型分析的桥梁变形值与实桥测试值之间的误差控制在8%之内，而关于应变值的计算误差也控制在8%之内。

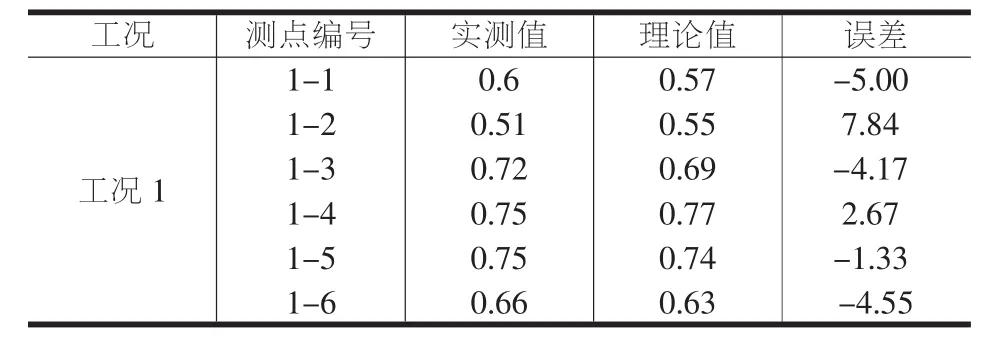
表3 模型分析挠度值与试验值对比

表4 模型分析应变值与试验值对比

3 结论

本文提出一种实腹式和空腹式双曲拱桥拱肋纵梁截面的建模设计方法，并通过实桥的静载测试结果进行对比分析。有限元结果与实桥静载试验结果对比表明，二者挠度误差在8%以内，应变误差在15%以内，因此本文提出的双曲拱建模方法具有较高的计算分析精度。

[1]王彬，李青宁.双曲拱桥承载能力试验检测评定[J].建筑结构，2010（S2）：678-682.

[2]李仁志，赵焕春，毛丽双.曲拱桥的加固与技术改造[J].东北公路，1996（3）：78-91.

[3]邵家邦.分析双曲拱桥病害原因和研究其加固方法[J].黑龙江科技信息，2010（32）：295-297.

[4]刘雄心，燕柳斌.有限元法在双曲拱桥计算中的研究[J].广西大学学报（自然科学版），2006，31（1）：5-9.

[5]王敏强，王乐，张桓，等.空腹式双曲拱桥有限元分析与试验研究[J].武汉大学学报（工学版），2005，38（5）：88-93.

[6]曲淑英.一种计算板、壳结构的简便方法[J].山东建筑工程学院学报，1996，11（4）：40-44.

[7]王星，徐伟良.板锥网壳结构的实用计算方法[J].浙江工业大学学报，2002，30（1）：75-77.

[8]程章宏，顾萍.双曲拱桥有限元分析中建模方法研究[J].上海公路，2008（4）：52-54.

[9]于天来，于海波.双曲拱桥拱上建筑联合作用的研究[J].城市道桥与防洪，2010（3）：123-126.