基于MF-SVD的滚动轴承振动信号故障特征提取方法研究

萨其日拉

(东北石油大学 石油工程学院，黑龙江 大庆 163318)

基于MF-SVD的滚动轴承振动信号故障特征提取方法研究

萨其日拉

(东北石油大学 石油工程学院，黑龙江 大庆 163318)

极值域均值模式分解(EMMD)在抑制端点效应、算法精度、计算耗时等方面均比经验模式分解(EMD)算法和自适应时变滤波分解(ATVFD)有着明显的优势，能够有效地对旋转机械振动信号进行故障特征提取，由于现场信号通常掺杂大量噪声，严重影响了EMMD的分解精度。针对该问题，提出了基于形态滤波-奇异值(MF-SVD)的去噪方法，并将其与EMMD相结合，建立了一种新的故障特征提取方法。实验结果表明： 该方法能够有效、准确地提取旋转机械滚动轴承内圈损伤的故障特征，有着良好运算速度和精确度。

极值域均值模式分解 形态滤波 奇异值分解 特征提取

1998年由N.E. Huang等人[1]提出一种新的时频分析法HHT(hilbert-huang transform)，能够有效地对非线性、非平稳信号进行分析，同时具有良好的自适应性，在机械故障诊断领域中HHT法已得到广泛的应用，并取得了良好的效果。但是N.E. Huang也指出该方法尚有不足之处，如三次样条插值的“过包络”和“欠包络”、端点效应以及模态混叠问题[2-3]。近年来，经过专家学者的不断研究，出现很多经验模式分解(EMD)的改进方法，其中较为先进的为自适应时变滤波分解法(ATVFD)和极值域均值模式分解法(EMMD)。经研究表明，EMMD法与ATVFD法和EMD法相比，具有有效抑制端点效应、高分解精度和更快的运算速度的特点。

但是，现场采集的振动信号通常掺杂大量噪声，大部分为随机噪声和局部冲击干扰，这些噪声同样进行EMMD分解计算。因此，在对信号分析之前有必要对其进行预处理，去除各种噪声干扰影响，提高EMMD法的分解质量和信号分析的可靠性和精度。

针对非线性、非平稳的机械振动信号有很多去噪方法，如沈路[4]等利用形态滤波对齿轮振动信号滤波消噪提取了故障特征，脉冲噪声干扰得到了有效抑制，随机噪声也得到了削弱，但是随机噪声还是比较明显，信号依然受到噪声干扰。曾作钦[5]等利用奇异值分解对信号进行预处理后再进行EMD法分解，取得比直接EMD法分解更好的效果，但是该方法对窄带脉冲的去噪效果不甚理想。

因此，文中提出了一种基于形态滤波-奇异值(MF-SVD)和EMMD的振动信号故障特征提取方法。该方法先将实测现场信号进行基于MF-SVD法去噪，滤除随机噪声信号和局部强干扰噪声，再进行EMMD分解，得到固有模态函数(IMF)分量，从而提取故障特征。实验结果表明： 该方法能够有效、准确地提取滚动轴承内圈损伤的故障特征，还可抑制端点效应，有着良好运算速度和精确度。

1 EMMD算法原理及实测信号中噪声影响

1.1 EMMD算法原理

EMMD法是基于EMD法和ATVFD法的一种改进算法，其计算局部均值既不同于EMD法的基于局部极值包络，也不同于ATVFD法的基于定积分中值定理原理的均值曲线[6]。

对于原信号数据求出所有N个局部极值点，不需区分局部极大值和局部极小值，组成{e(ti)}，其中ti(i=1, 2, …,N)为第i个局部极值点的时间位置。于是信号行x(t)的数据序列值，对ti与ti+1时刻极值点间的局部均值可计算如下：

(1)

考虑信号数据在极值点间一般是均匀变化的，其均值位置可视为在两极值点的中点处，即tξ=(ti+ti+1)/2，这样

(2)

同理，ti+1与ti+2时刻极值点间的局部均值mi+1为

(3)

这样，mii+ti+1)/2为第i个极值点和第i+1个极值点信号的局部均值，而mi+1i+1+ti+2)/2为第i+1个极值点和第i+2个极值点信号的局部均值。现用2个相邻局部均值mi和mi+1加权平均作为ti+1处极值点的局部均值mi(ti+1)，即

(4)

(5)

利用式(4)可以得到信号各局部极值点处的局部均值m(0),m(t1),m(t2), …,m(tn)，再使用3次样条插值函数对其进行曲线拟合得到局部均值m1(t)，从而得到第1个IMF分量h1(t)：

h1(t)=x(t)-m1(t)

(6)

这时h1(t)可能不满足IMF定义，需要再次筛选：

h11(t)=h1(t)-m11(t)

(7)

重复式(7)直到满足筛选停止准则：

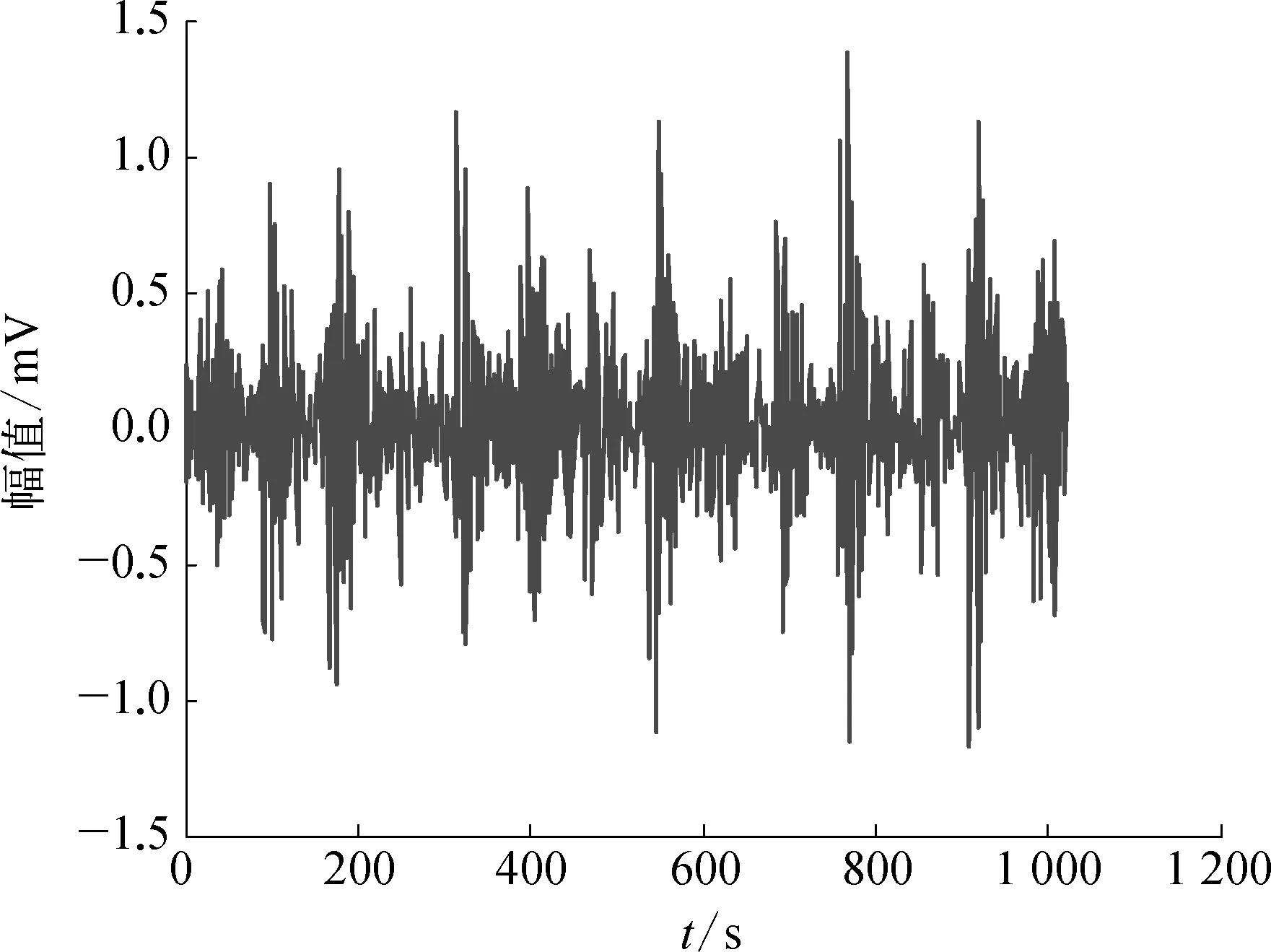
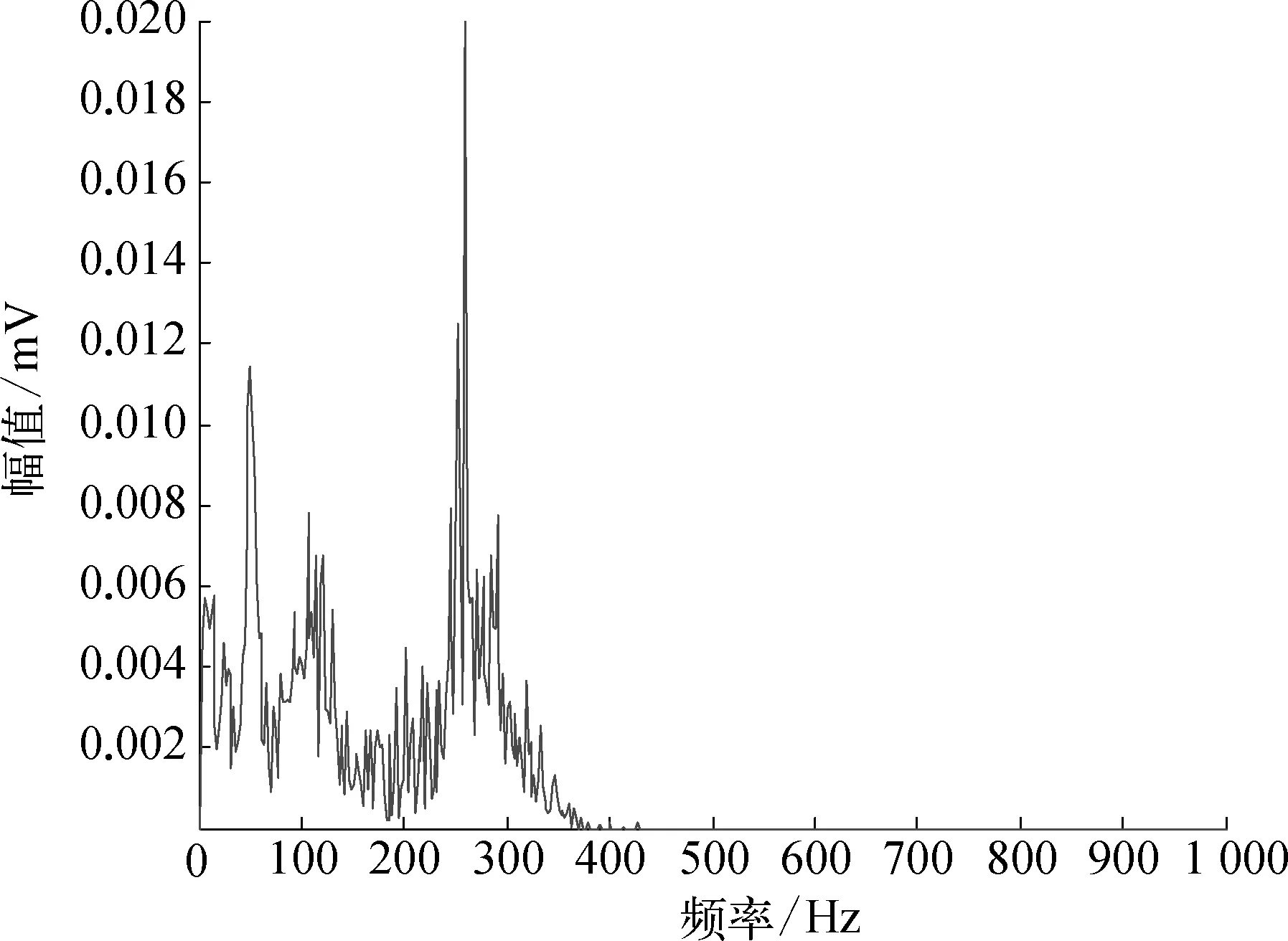
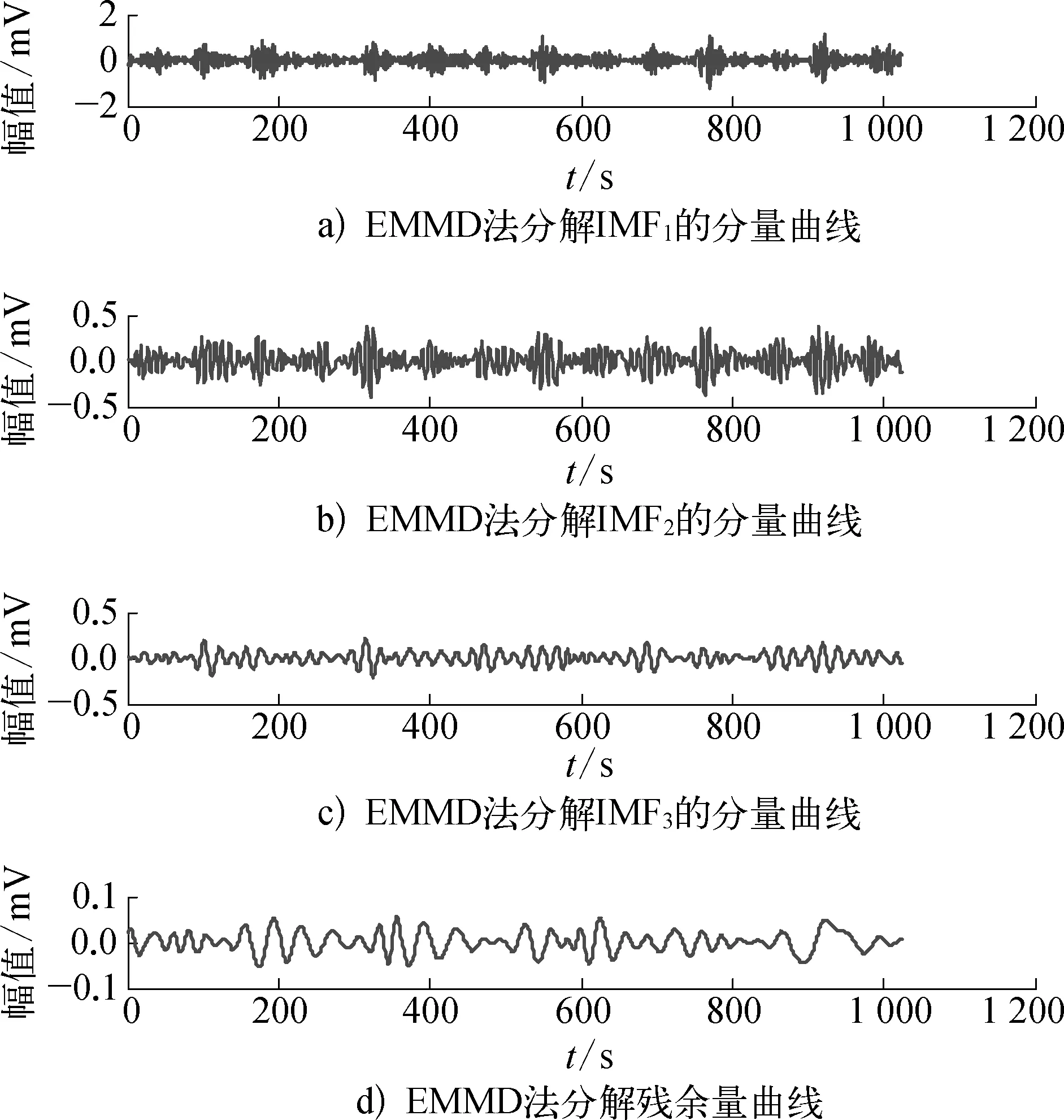
0.2

(8)

重复k次得到：

h1k(t)=h1(k-1)(t)-m1k(t)

(9)

此时，h1k就是第1个IMF分量，表示为C1(t)=h1k(t)，残余信号：

r1(t)=x(t)-C1(t)

(10)

以r1作为待分析信号重复以上步骤，直到所得剩余部分为单调信号或其值小于给定值时，分解完毕，得到所有IMF分量C2(t),C3(t),C4(t), …,Cn(t)以及残余分量Rn(t)，这时信号可表示为所有IMF分量和残余量之和：

(11)

实测信号中往往夹杂了大量的噪声，而该噪声是不需要分解的干扰量，不仅增加了EMD分解的层数，使得分解时效性下降，而且过多的分解使得模态间累积泄漏加剧、边界误差不断累加，严重时会使EMD分解失去实际的物理意义。

1.2 实测信号中噪声的影响

某旋转机械滚动轴承振动信号如图1所示。分别对实测信号进行EMD法和EMMD法分解，得到各IMF分量，由于篇幅限制，只取前4个分量，如图2，图3所示，相应的希尔伯特边际谱如图4，图5所示。

从图3，图5中可以看出EMMD法在分解精度、端点效应抑制和计算耗时上均优于EMD法，但是实测信号中大量噪声同样参加了计算过程，从分解出第1个IMF分量开始，逐渐污染整个分解过程，尤其在50 Hz和120 Hz频率附近，积累出能量很大的干扰量，影响了计算结果，需要对信号进一步去噪。

图1 实测滚动轴承振动信号示意

图2 EMD法分解各IMF分量及残余量曲线示意

2 MF和SVD相结合的去噪方法

2.1 形态滤波原理

与传统的处理方法相比，数学形态学具有计算简单、实用性好、时延较小等特点，为振动信号去噪预处理提供了一种新的滤波方法[7]。

图3 EMMD法分解各IMF分量及残余量曲线示意

图4 EMD算法边际谱曲线示意

图5 EMMD算法边际谱曲线示意

数学形态学的基本运算包括： 腐蚀运算、膨胀运算、开运算和闭运算。设原始信号f(n)为定义在Df=(0, 1, 2, …,N-1)上的离散函数，定义序列结构元素g(n)为Dg=(0, 1, 2, …,M-1)上的离散函数，且N≥M，则f(n)关于g(n)的的膨胀运算和腐蚀运算分别为

(f⊕g)(n)=max(f(n-m)+g(m))

(12)

(fΘg)(n)=min(f(n+m)-g(m))

(13)

f(n)关于g(n)的开运算和闭运算分别为

(f∘g)(n)=(fΘg⊕g)(n)

(14)

(f·g)(n)=(f⊕gΘg)(n)

(15)

其中m∈0, 1, 2, …,M-1；n∈0, 1, 2, …,N-1。

膨胀运算除去负脉冲并平滑了正脉冲；腐蚀运算除去正脉冲并平滑了负脉冲；开运算除去正脉冲并保留了负脉冲；闭运算除去负脉冲并保留了正脉冲。为了同时去除正、负两种噪声，采用开闭运算的级联形式，定义形态开闭和闭开滤波器：

Foc(f(n))=(f∘g·g)(n)

(16)

Fco(f(n))=(f·g∘g)(n)

(17)

为有效抑制脉冲干扰，本文采用开闭和闭开组合滤波器，定义：

y(n)=[Foc(f(n))+Fco(f(n))]/2

(18)

研究表明： 结构元素越复杂，滤波能力越强，计算量也越大[8]。为了确保EMMD法分解质量，减少对信号中有用信息的损失，选择扁平形结构元素是最简单、也是最有效的方法，综合考虑本文选择扁平形结构元素。

2.2 SVD原理

奇异值分解技术在故障诊断领域已有成功的应用。已广泛应用于信号降噪或提取信号中的周期成分。文中利用SVD技术，根据奇异值分布曲线确定降噪阶次，进行SVD降噪。

假设某故障机械系统的测试信号为xl(l=1, 2, 3, …)，可由它重构1个m×n维重构相空间Dm[9]

若振动信号中包含有一定的噪声，则Dm可表示成Dm=D+W+V，其中D,W,V分别是光滑信号、故障信息、噪声对应的Dm中的轨迹矩阵，也可以将W和V视为对D矩阵的摄动。现在仅知道Dm而不知道D和W，但是可以根据D和W的一些特点研究其奇异值情况对Dm做奇异值分解，Dm=USV′,U∈Rm×n,V′∈Rm×n，且UU′=I,VV′=I。S是m×n矩阵，对角线元素为λ1,λ2, …,λk,Dm的秩为k且k=min(m,n)，一般取m≪n，λ1≥λ2≥…≥λk称为Dm的奇异值，U和V分别表示左右奇异阵。

2.3 MF-SVD信号去噪方法

基于MF-SVD法和EMMD法的振动信号故障特征提取方法，即先将实测现场信号进行基于MF-SVD法去噪，结合形态滤波对振动信号可以有效抑制脉冲噪声干扰和奇异值分解针对随机噪声信号滤波效果明显的优点，滤除随机噪声信号和局部强干扰噪声，再进行EMMD法分解，得到IMF分量，从而提取故障特征。

3 故障诊断实验

本文实验对象为某天然气公司的制冷压缩机，是美国约克公司生产的RWB(II)-496型螺杆压缩机，单台机组设计处理天然气量为4 960 m3/h，压缩介质为丙烷，转速为2 150 r/min，测点选择在电机与螺旋杆之间连轴器靠近电机的支撑轴承上，轴承的型号为HRB—N205EM，参数见表1所列。

表1 轴承参数

在生产过程中发现测点在线振动监测装置显示振动异常，检修发现支撑轴承内圈有中度损伤，其特征频率应为f=256.11 Hz。测得振动信号如图6所示，其频谱如图7所示，根据频谱图不能判断出具体故障原因。

图6 振动信号时域波形曲线示意

图7 振动信号频谱曲线示意

对信号直接进行EMMD法分解，其边际谱分析如图8所示，根据边际谱曲线所示，虽然频率在260 Hz附近有较高的振幅，但在50 Hz和100 Hz附近同样出现了较大的振幅，形成很大的干扰，而且边界抖动幅度大，这都说明在直接EMMD法分解过程中，由于混有现场强噪声，使整个分解过程受到污染，致使出现端点效应和模态混叠问题，影响了边际谱的刻画，对于滚动故障诊断来说无法准确判断其故障类型。

图8 直接EMMD法分解边际谱曲线示意

采用MF-SVD法去噪和EMMD法相结合的故障特征提取方法，对信号进行处理。去噪后的信号如图9所示，其IMF分量如图10所示，其边际谱如图11所示。可以看出，边际谱曲线频率仅在255.6 Hz处幅度最大，其他频率干扰消除，去噪效果明显，有效地抑制了边界效应和模态混叠问题，可以准确判断出故障类型为滚动轴承内圈损伤。

图9 MF-SVD去噪后信号时域曲线示意

图10 EMMD法分解各IMF分量及 残余信号曲线示意

4 结束语

笔者针对现场实测信号掺杂强噪声影响EMMD法分解质量和结果的问题，提出了一种基于MF-SVD法与EMMD法分解相结合的故障特征提取方法。该方法先对实测现场信号采用MF-SVD法去噪，滤除随机噪声信号和局部强干扰噪声，弥补了形态滤波去噪方法对于随机噪声信号处理的不足和奇异值分解对于脉冲干扰噪声处理的不足，然后进行EMMD法分解，得到IMF分量，从而提取故障特征。

图11 去噪后经EMMD法分解边际谱曲线

实验结果表明： 该方法能够去除随机噪声和局部强干扰噪声，效果明显，能够有效、准确地提取滚动轴承内圈损伤的故障特征，可抑制端点效应，有着良好的运算速度和精确度。

[1] 王宏禹.信号处理相关理论综合与统一法[M].北京： 国防工

业出版社，2005.

[2] Huang N E, Shen Z, Long S R. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society of London, 1998， 45(04)： 903-995.

[3] Wu Zhaohua, Huang N E. Ensemble Empirical Mode Decomposition： a Noise-assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009(01)： 1-41.

[4] 沈路，杨富春，周晓军，等.基于改进EMD与形态滤波的齿轮故障特征提取[J].振动与冲击，2010，29(03)： 154-157.

[5] 曾作钦.基于奇异值分解的信号处理方法及其在机械故障诊断中的应用[D].广州： 华南理工大学，2011.

[6] 屈梁生，张西宁，沈玉娣.机械故障诊断理论与方法[M].西安： 西安交通大学出版社，2009.

[7] 李舜酩，李香莲.振动信号的现代分析技术与应用[M].北京： 国防工业出版社，2008.

[8] 李兵，张培林，米双山.机械故障信号的数学形态学分析与智能分类[M].北京： 国防工业出版社，2011.

[9] 韩清凯，于晓光.基于振动分析的现代机械故障诊断原理及应用[M].北京： 科学出版社，2010.

[10] 刘佳宝,梁奕,徐漫江.一种过程数据趋势特征提取方法.化工自动化及仪表,2012,39(07)： 850-853.

[11] 刘继承,聂品磊,杨宏宇,等.基于形态滤波和HHT的滚动轴承故障特征提取.化工自动化及仪表,2014,41(05)： 529-532,562.

Study on Fault Characteristics Extraction for MF-SVD Based Rolling Bearing Vibration Signal

Sachsla

(College of Petroleum Engineering, Northeast Petroleum University, Daqing, 163318, China)

In terms of calculation precision, restraining boundary effect and computation time, extremum field mean mode decomposition(EMMD) has obvious advantage comparing to empirical mode decomposition(EMD) and adaptive time varying filter decomposition(ATVFD). It can effectively extract machinery vibration signal fault characteristics. As the measured field signals are often mixed lots of noise, which influences EMMD decomposition quality seriously. Aiming at the problem, a new extracting fault feature method which is based on morphological filters-singular value decomposition (MF-SVD) denoising method, combined with EMMD, is put forward. The experimental results show fault features of rolling bearing inner ring damage can be effectively and accurately extracted. It has a good calculation speed and accuracy.

extremum field mean mode decomposition; morphological filters; singular value decomposition; feature extraction

黑龙江省长江学者后备计划资助(2012CJHB005)。

萨其日拉(1994—)，男，蒙古族人，就读于东北石油大学石油工程学院，研究方向为油田工艺及设备技术。

TP273

A

1007-7324(2017)03-0031-06

稿件收到日期： 2017-02-27，修改稿收到日期： 2017-04-27。