基于故障树的SIS可用性分析

徐飞，谭壮壮

(中国石油海洋集团工程有限公司，北京 100028)

基于故障树的SIS可用性分析

徐飞，谭壮壮

(中国石油海洋集团工程有限公司，北京 100028)

安全失效概率(PFS)是衡量安全仪表系统(SIS)性能优劣的重要指标之一。在阐述SIS表决结构的设计特性及其可用性关系基础上，研究了基于故障树SIS表决结构的可用性关系，并通过具体实例进行验证。研究结果表明： 表决结构故障树可用性与设计特性不能完全相符，更加准确的可用性模型尚需进一步研究。

安全仪表系统 故障树 可用性 安全失效概率 表决结构

安全仪表系统(SIS)已广泛应用于石油、化工及冶金等行业中，是保障生产安全的重要措施，其安全性和可用性是衡量SIS性能优劣的两大重要指标[1-2]。因安全性直接反应了SIS生产安全有效的防护能力，是设计SIS的前提条件，也是诸多学者研究的对象，但在实际应用中，人们希望SIS也具有一定的可用性，若系统可用性差，将使生产无法正常进行，从而造成巨大的经济损失[3-4]。因此，对SIS进行可用性定量研究也有一定的意义。

安全失效概率(PFS)是可用性的具体量化指标，其定量计算模型主要通过可靠性框图法、故障树法和马尔科夫(Markov)模型法三种方法建立[2-4]。在实际工程应用中，可靠性框图计算简单但是精确度不高；Markov模型虽然精确度高且能反应系统的动态性能，但当系统较大或系统状态较多时，模型的建立和计算都会变的异常复杂；故障树因模型计算量及精确度都较为均衡而在实际中应用较广。

表决结构故障树可用性模型在文献[5]、文献[6]中进行了主要描述，本文基于SIS表决结构设计特性的可用性关系，对文献[5]、文献[6]所述的故障树可用性模型进行分析研究。

1 SIS表决结构设计特性可用性分析

SIS常见表决结构主要有“1oo1”，“1oo2”，“2oo2”，“2oo3”，其主要设计特性：“1oo1”结构是1个最小的系统，不具备容错的能力，对设备的各种失效模式没有保护能力，如果通道发生检测到的安全失效或未检测到的安全失效，系统就将发生安全失效；“1oo2”结构系统危险失效概率很低，但是安全失效概率却增大了，任一通道的安全失效会造成系统的安全失效，容易造成受控系统的误停车；“2oo2”结构将2个通道的输出并联，这样可以保护单一通道的安全失效不致使系统的安全失效；“2oo3”结构中3个通道两两串联构成“表决”电路，以确定当前系统的输出[5]。

在实际应用中，“1oo1”表决结构安全性相对较低，“1oo2”表决结构适用于安全性很高的情况，但可用性差；“2oo2”表决结构适用于安全性要求一般，而可用性要求较高的情况；“2oo3”表决结构的安全性和可用性保持相对均衡，可用于安全性、可用性均较高的情况[7]。因此，从表决结构的设计特性可以得出，对于同一元件，几种表决结构的可用性关系应该是PFS1oo2>PFS1oo1>PFS2oo3>PFS2oo2，即“2oo2”可用性最高，“2oo3”次之，“1oo1”较低，“1oo2”最低，但通过故障树建立的SIS可用性模型并不能确定上述表决结构的可用性关系。

2 基于故障树SIS可用性分析

2.1 SIS故障树可用性模型

文献[5]、文献[6]通过故障树建立了可用性模型，以“1oo1”为例进行简要说明，“1oo1”结构系统安全失效的故障树如图1所示。

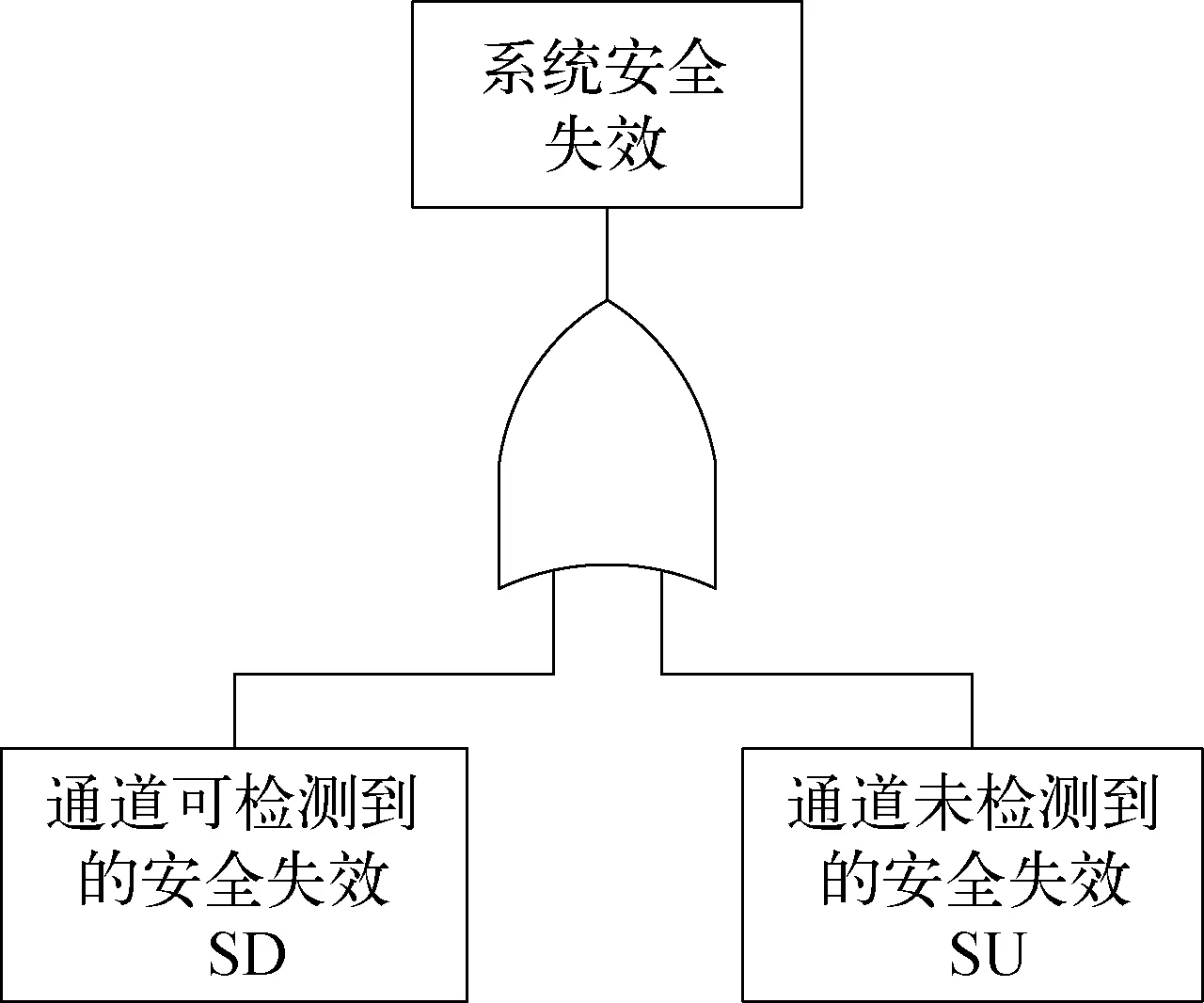
图1 “1oo1”故障树模型示意

如果通道发生检测到的安全失效或未检测到的安全失效，那么系统将发生安全失效。在通道的失效概率很低的情况下，系统安全失效概率PFS近似为

PFS1oo1=λSD×TS+λSU×TS

(1)

式中：λSD——可检测的安全失效概率，λSD=λS×DC;λS——安全失效概率，λS=λ×(1-Q);λ——元件失效概率；Q——安全失效比率；DC——诊断覆盖率；λSU——未检测的安全失效概率，λSU=λS×(1-DC)；TS——停车后的重启时间。

文献[5]、文献[6]利用上述方法分别得出“1oo2”,“2oo2”及“2oo3”可用性模型如下：

PFS1oo2=(λSUC+λSDC+2λSDN+2λSUN)×TS

(2)

PFS2oo2=λSUC×TS+λSDC×TS+

(λSDN×RT+λSUN×TI)2

(3)

PFS2oo3=3λSUC×TS+3λSDC×TS+

3(λSDN×RT+λSUN×TI)2

(4)

式中：λSUC——未检测的共因安全失效概率，λSUC=λSU×β，β——共因失效因子；λSDN——可检测的不共因安全失效概率，λSDN=λSD×(1-β)；λSDC——可检测的共因安全失效概率，λSDC=λSD×β;λSUN——未检测的不共因安全失效概率，λSUN=λSU×(1-β);TI——周期性功能测试间隔；RT——在线修复时间。

2.2 SIS可用性分析比较

通过故障树模型[5-6]及相应PFS公式可以看出，“1oo1”与“1oo2”公式构成类似，而“2oo2”与“2oo3”公式构成类似，故分别进行分析比较。

1) “1oo1”与“1oo2”，“2oo2”与“2oo3”的可用性分析。

PFS1oo2-PFS1oo1=(λSDN+λSUN)×TS

(5)

PFS2oo3-PFS2oo2=2λSUC×TS+2λSDC×

TS+2(λSDN×RT+λSUN×TI)2

(6)

由上述分析可以得出，表决结构PFS关系分别是：PFS1oo2>PFS1oo1,PFS2oo3>PFS2oo2，与表决结构设计特性一致。

2) “1oo1”分别与“2oo2”和“2oo3”以及“1oo2”分别与“2oo2”和“2oo3”的可用性分析。文中以“1oo1”与“2oo2”为例进行可用性分析比较。

PFS1oo1-PFS2oo2=λSUN×(TS-λSUN×TI2)+

λSDN×(TS-λSDN×RT2-2×λSUN×TI×RT)

(7)

上述分析结果中TS和RT通常以小时为单位，数量级别不超过102，TI通常以年为单位，若以1a计，数量级别不超过104，λSDN主要受λ,DC,β,Q这4个变量参数影响，通常其数量级小于10-5，从而λSDN×RT2数量级小于10-1，2×λSUN×TI×RT数量级别约为101，因而TS-λSDN×RT2-2×λSUN×TI×RT结果通常为正值。另TI2的数量级别在107，当故障率λ取值在10-7级别时，TS-λSUN×TI2结果基本为正值；当故障率λ取值在10-5级别时，TS-λSUN×TI2结果往往为负值。综合两部分的计算结果，式(7)最后的正负关系不能确定，即“1oo1”与“2oo2”可用性关系也不能定论，这与表决结构设计特性不能完全相符。

同理可对“1oo1”与“2oo2”，“1oo2”与“2oo2”，“1oo2”与“2oo3”的可用性进行分析比较，通过研究表明： 因影响参数取值区间的变化，表决结构之间同样存在上述可用性关系的不确定性，导致不能与表决结构设计特性完全相符。

3 SIS可用性实例分析

通过具体数据，对表决结构之间的可用性关系进行了验证分析。由于PFS计算主要受7个参数影响，为了研究方便，影响因素只考虑参数的自相关性，暂不考虑参数之间的互相关性，利用Matlab软件对PFS影响参数分析进行仿真，其参数取值均为常用范围，见表1所列。故障树模型λ对PFS的影响分析如图2所示。

表1 SIS参数取值

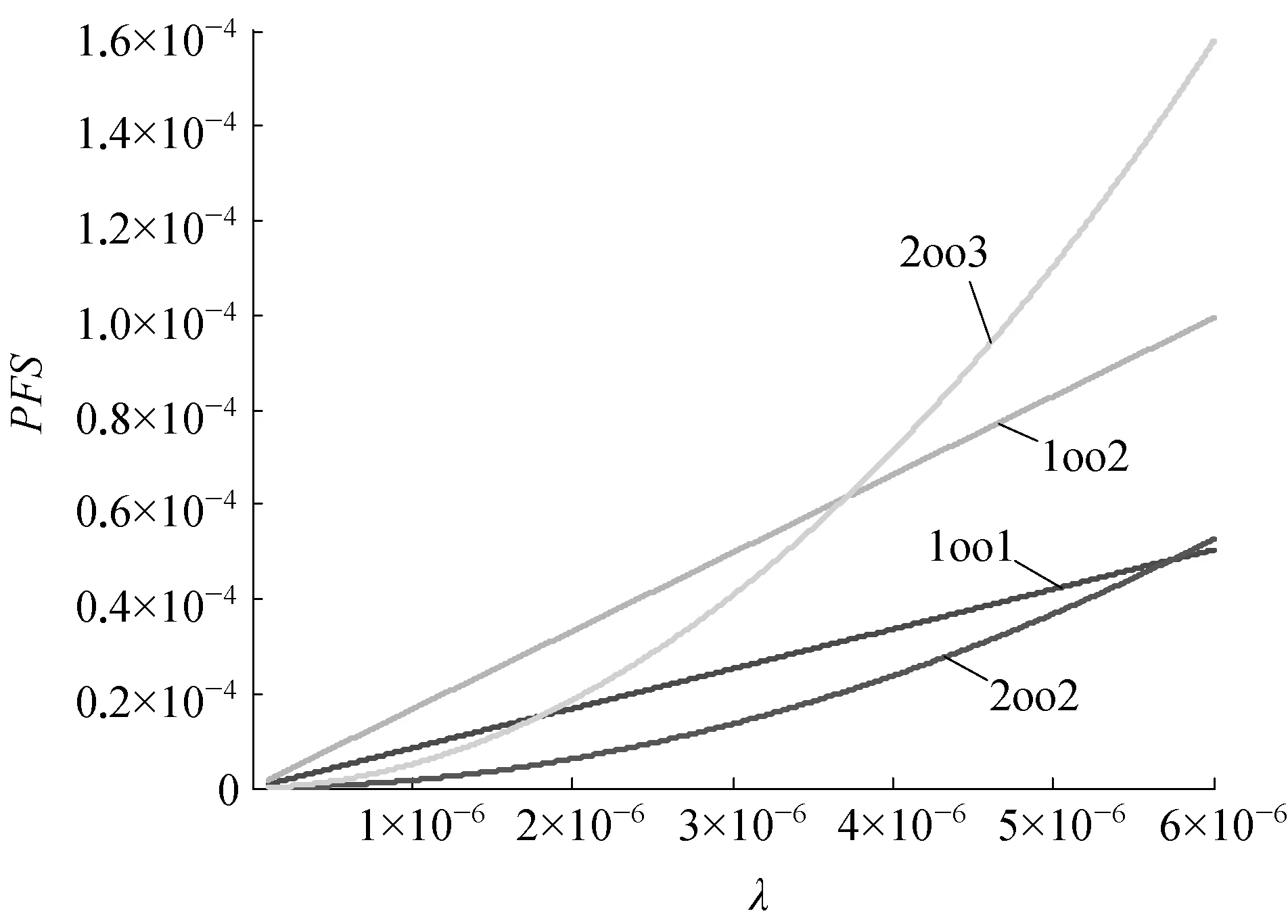
图2 故障树模型λ对PFS的影响分析示意

从图2可清晰地看出，随着λ的增大，其他因素不变的情况下，在不同λ取值区间内，四种表决结构PFS大小关系均有变化，即可用性关系存在不确定性。现选取具体的λ值，计算结果见表2所列，并最终分析得出可用性关系见表3所列。

表2 PFS计算结果

表3 表决结构可用性关系

根据图1及表3的结果，“2oo3”与“1oo1”，“1oo2”以及“2oo2”与“1oo1”，“1oo2”之间的关系会因故障率λ的取值不一样而出现变化，仅在λ取值较小的情况下，四种表决结构可用性关系与设计特性相符；但随着λ取值增大，故障树建立的模型不符合结构设计特性。

4 结束语

1) 基于故障树的可用性模型，对于同一元器件，冗余结构“1oo1”与“1oo2”，“2oo2”与“2oo3”之间的可用性关系为PFS1oo2>PFS1oo1,PFS2oo3>PFS2oo2，与其设计特性相符；“1oo1”分别与“2oo2”和“2oo3”以及“1oo2”分别与“2oo2”和“2oo3”之间随着影响参数取值不同，相互之间的可用性关系不能确定，与其设计特性不能完全吻合。

2) 基于故障树的可用性模型在实际应用中具有一定的局限性，对于相关参数相对较小的场合，特别是λ取值较小时，计算模型可与设计特性可用性保持一致。

3) 基于故障树的可用性模型与表决结构设计特性不完全符合的主要原因是由于参数TS和TI数量差别较大，而一般情况下TI是TS的数百倍，在式(1)，式(2)未考虑TI周期内的安全失效检测，从而导致各表决结构可用性出现不同的关系。

4) 工作中，应充分考虑各参数在模型中的应用意义，如何确定更加准确的可用性模型尚需进一步研究。

[1] IEC. IEC 61508 Functional Safety of Electrical/Electronic/Programmable Electronic Safety — Related Systems[S]. IEC, 2010.

[2] IEC. IEC 61511 Functional Safety — Safety Instrumented Systems for the Process Industry Sector[S]. IEC, 2003.

[3] 王秉义，张惠良，左信.SIS安全联锁功能可用性分析[J].石油化工自动化，2012，48(01)： 13-17.

[4] 魏华.安全仪表的可靠性和可用性分析[J].石油化工自动化，2009，45(01)： 10-19.

[5] 阳宪惠，郭海涛.安全仪表系统的功能安全[M].北京： 清华大学出版社，2007.

[6] William M.Control Systems Safety Evaluation and Reliability[M]. USA： ISA, 1998： 335-419.

[7] 靳江红，庞磊，赵寿堂，等.安全仪表系统的可用性分析及其定量评估[J].测控技术，2014，33(06)： 9-12.

Availability Analysis Based on Fault Tree for Safety Instrumented System

Xu Fei, Tan Zhuangzhuang

(China National Petroleum Offshore Engineering Co. Ltd., Beijing, 100028, China)

Probability of failing safety is one of important indicators to measure performance of safety instrumented system (SIS). Based on expounding of design characteristics and availability of SIS voting configurations, the availability of SIS voting configurations based on fault tree analysis (FTA) is studied. It is verified with some special actual cases. The results show the availability of SIS voting configurations is not completely consistent with design characteristics. More accurate availability model needs to be further studied.

safety instrumented system (SIS); fault tree analysis (FTA); probability of failing safety (PFS); voting configurations

徐飞(1984—)，男，安徽桐城人，2009年毕业于中国石油大学(北京)控制理论与控制工程专业，获硕士学位，现就职于中国石油集团海洋工程有限公司，从事海上石油平台仪表电气设计工作，任工程师。

TP273

A

1007-7324(2017)03-0041-03

稿件收到日期： 2017-02-03，修改稿收到日期： 2017-03-14。