一种基于空间剖分的射线追踪算法的研究

李悦园，谢礼节，郑羊城

(南京邮电大学 电子科学与工程学院，江苏 南京 210003)



一种基于空间剖分的射线追踪算法的研究

李悦园，谢礼节，郑羊城

(南京邮电大学 电子科学与工程学院，江苏 南京 210003)

传统的射线追踪算法中都需要对射线和传播环境的物体进行相交测试，这样会浪费大量的时间，效率不高。因此提出一种基于空间剖分的射线追踪算法，其中心思想为建立传播环境进行几何模型，利用剖分软件(如Gmsh)去除物体所占有的空间后剖分传播环境，连立点、线、面、体之间的几何关系，再利用射线和剖分后的子单元的几何关系确定射线的传播路径。

几何光学；电波传播；射线追踪；空间剖分

0 引言

20世纪60年代，著名的物理学家Maxwell在总结前人众多工作的基础上并且提出了著名的Maxwell方程组[1]。这个方程组不仅很好地表明了电磁场的基本性规律，而且预言了电磁波的存在。实际上，差不多一切求解电磁的问题都能够化成在特定边界条件下Maxwell方程组的解[2]。此后，许多种电磁场数值方法由Maxwell方程组演变出来了。可以以求解结果精度的差异为依据，把电磁场数值方法划分成低频数值方法和高频方法两种。两种方法都有其各自的优点和缺点，低频数值方法的优点是具有相对较高的精度，缺点是对计算资源的需求量与目标尺寸的变大成正相关的关系，适用于电尺寸相对较小的目标。高频方法的优点是计算资源需求少、计算速度快，其缺点是不能对目标上的精细结构进行精确计算，适用于大尺寸目标。高频近似方法有几何光学法(GO)、物理光学法(PO)、几何绕射理论(GTD)[3-4]、物理绕射理论(PTD)、等效电磁流法(MEC)、弹跳射线法(SBR)[5-6]等，这些方法的基础都是射线追踪算法，此外地震波预测[7]也需要射线追踪算法，因此具有十分重要的研究意义。

基于空间剖分的射线跟踪方法是一种新提出的射线跟踪方法。它利用二维或三维空间的剖分子单元(二维为三角形，三维为四面体)之间的几何位置关系来实现射线的快速追踪，是目前计算速度比较快的电波传播射线分析方法[8]。此方法的核心是将二维或者三维空间分割成多个无缝且互不重叠的三角形或四面体子单元，再把发射源看成是若干根从源点发出的射线，并利用射线和每个子单元之间的空间矢量关系来计算所有射线的轨迹。这种方法可以避免射线和多面体面相交测试中所耗费的绝大部分时间[9]。限于篇幅本文主要介绍二维情况下的射线追踪算法。

1 算法分析

以三角形剖分形式对二维环境进行剖分，划分后形成的三角形的边可以分成两种:第一种边是在它的两边为两种不同的介质材料，所以射到这种边上的射线会产生反射现象，这种边叫做“实边”；第二种边是在它的两边为相同的介质，因此入射到这种边上的入射线会遵循原来的方向不改变，继续朝向前方射出，这种边叫做“虚边”。可以依据两种原则来剖分三角形:

(1)剖分三角形的时候应该使得三角形的数目尽可能减少。

(2)划分后三角形的一条边上只能有一种属性，即不是“实边”就是“虚边”，此外如果某条边是“实边”，则该边的介质的电磁特性完全相同。

1.1 射线在三角形间穿行

如图1所示，有射线自三角形T2的边E1射出，这个过程写成(E1,T2)，之后射线穿过虚边e2进到三角形T3之中，此过程可以写成(e2,T3)，因此射线经过三角形网格的历程表示为:

(E1,T2)→(e2,T3)→(e2,T2)→(e4,T7)→(E5,T7)→(e6,T8)→(e7,T6)→(E8,T6)→…

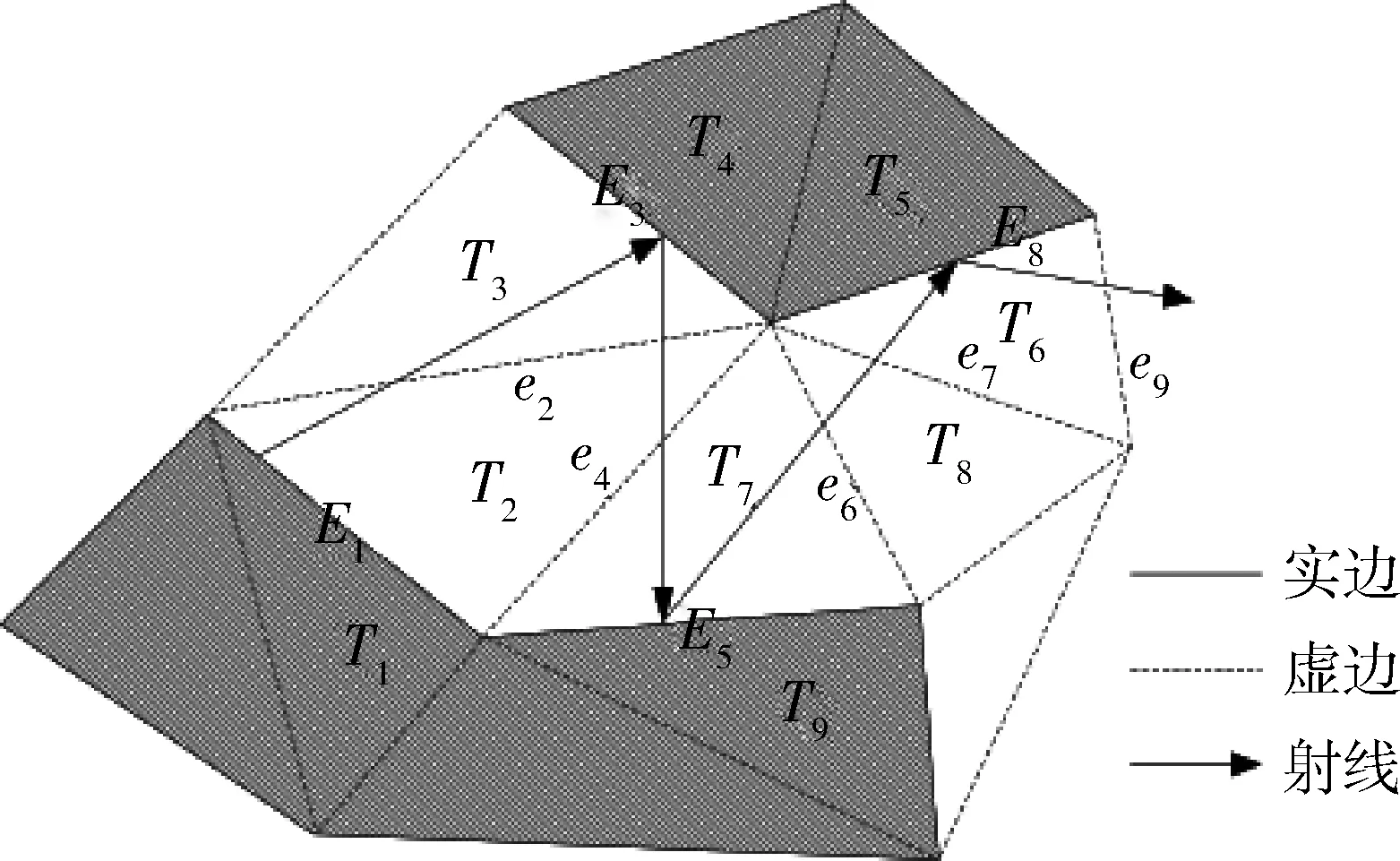
图1 射线经过三角形网格

1.2 穿出面判断算法

射线穿出边的判定算法过程，为了得到具有普遍性的结论，讨论射线入射到第k个三角形Tk的情况。

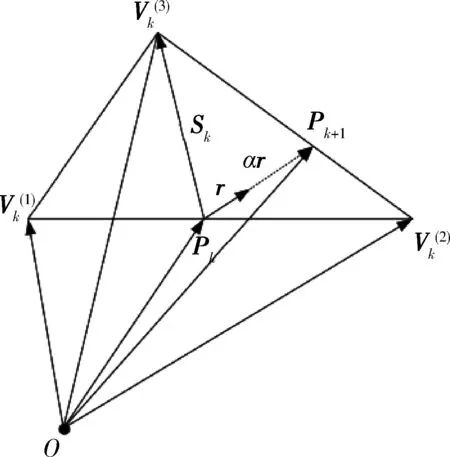
图2 求穿出点的位置矢量的示意图

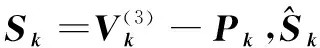
需要注意的是在这种方法中，当穿出边是“虚边”的时候，要显式算出“虚边”与射线的交点，但是射线轨迹的描述只需要用到“实边”与射线的交点，所以这种方法计算工作量会比较大。

现对该方法如下改进，令

(1)

其中

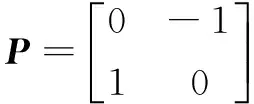
(2)

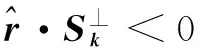
1.3 穿出点的位置矢量算法

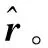
(3)

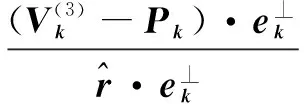
(4)

所以得到：

(5)

反射后的射线的方向矢量是：

(6)

1.4 空间数据结构的建立

如图3所示，建立一个二维矩形腔5λ×10λ的模型，将矩形腔分成3个三角形并建立如下的数据结构(λ=3)：

其中，node矩阵表示矩形上的5个点坐标，patch_node表示面和点的关系矩阵，line_node表示线和点的关系矩阵，line_patch表示线和面的关系矩阵，patch_line表示面和线的关系矩阵，line_norm表示线的法向量。

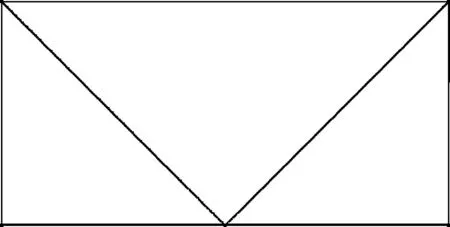
图3 二维矩形腔剖分结构图

数据结构建立好后，即可根据上述的基于空间剖分的射线追踪方法，追踪的过程中当遇到实线时候会发生反射，直至停止追踪即可得到射线的传播路径。

2 射线追踪在电磁散射应用

对于二维问题有：利用面等效原理计算散射场时，散射场由表面电流(z方向)和磁流(xoy面内)产生，然后利用辅助位求解散射场。

(7)

(8)

当处于远区时：

(9)

式(7)可以化为：

(10)

式(8)可以化为：

(11)

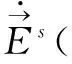
(12)

回波宽度定义为：

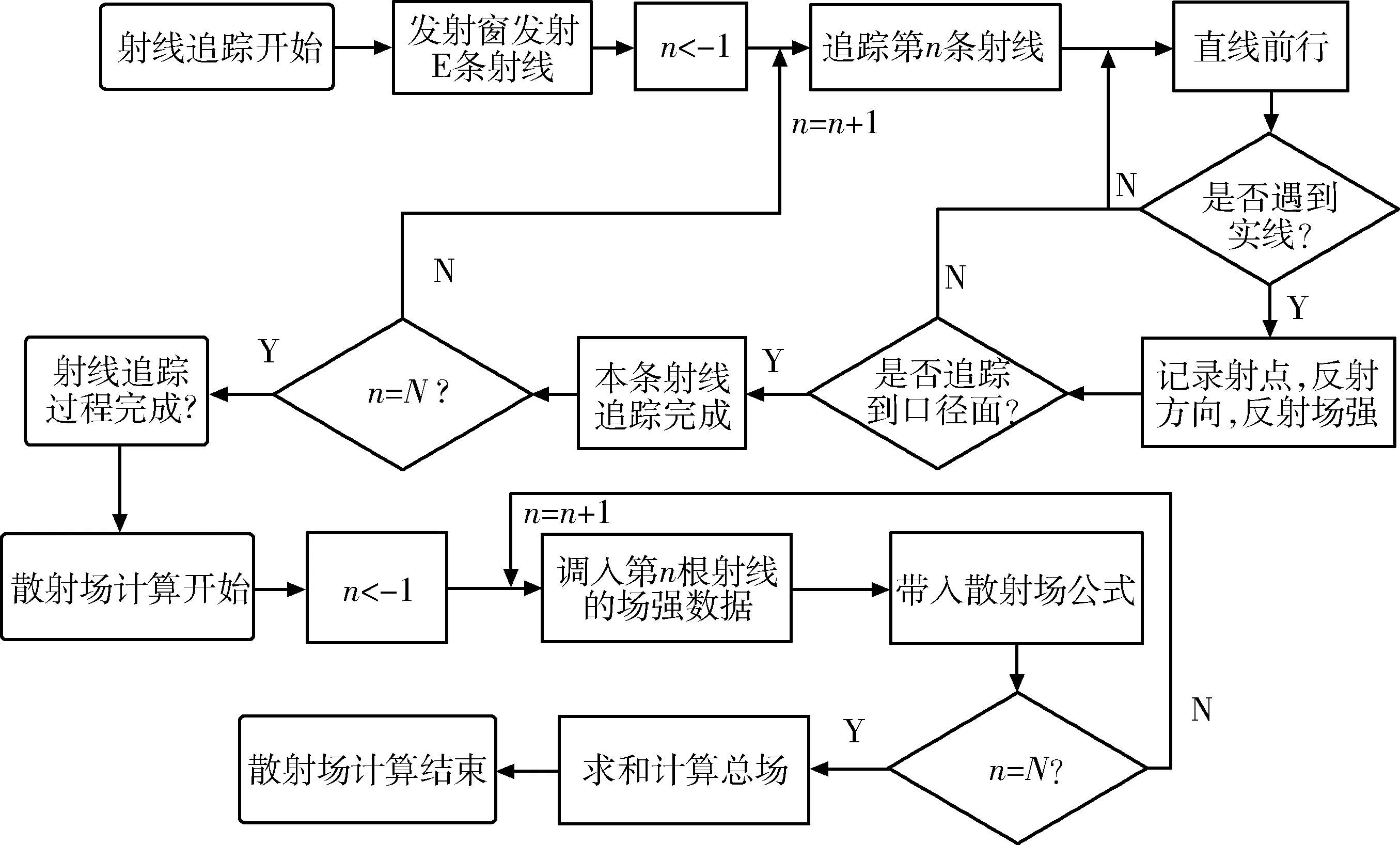
图7 计算流程

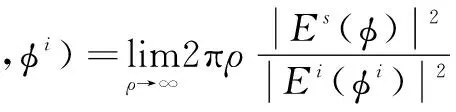
(13)

所以散射宽度的近似表达式为：

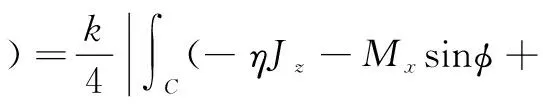
(14)

假设TM波入射，计算二维金属圆柱体的散射场，图4所示为一圆柱体截面，为了计算简单，选择入射波为垂直于z轴入射的TM平面波。

假设入射波的波长为λ=3 m，圆柱半径

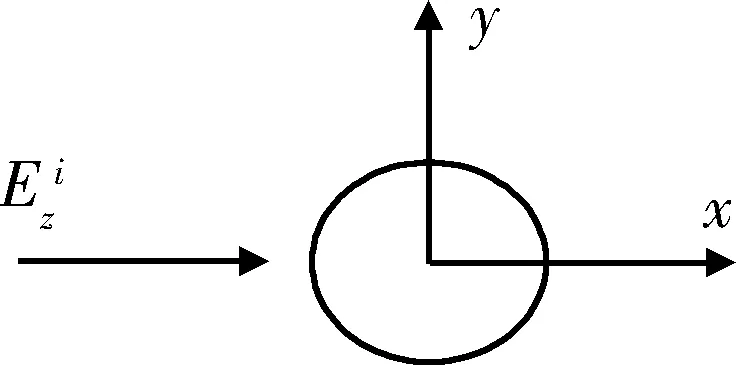
图4 面波入射二维金属圆柱

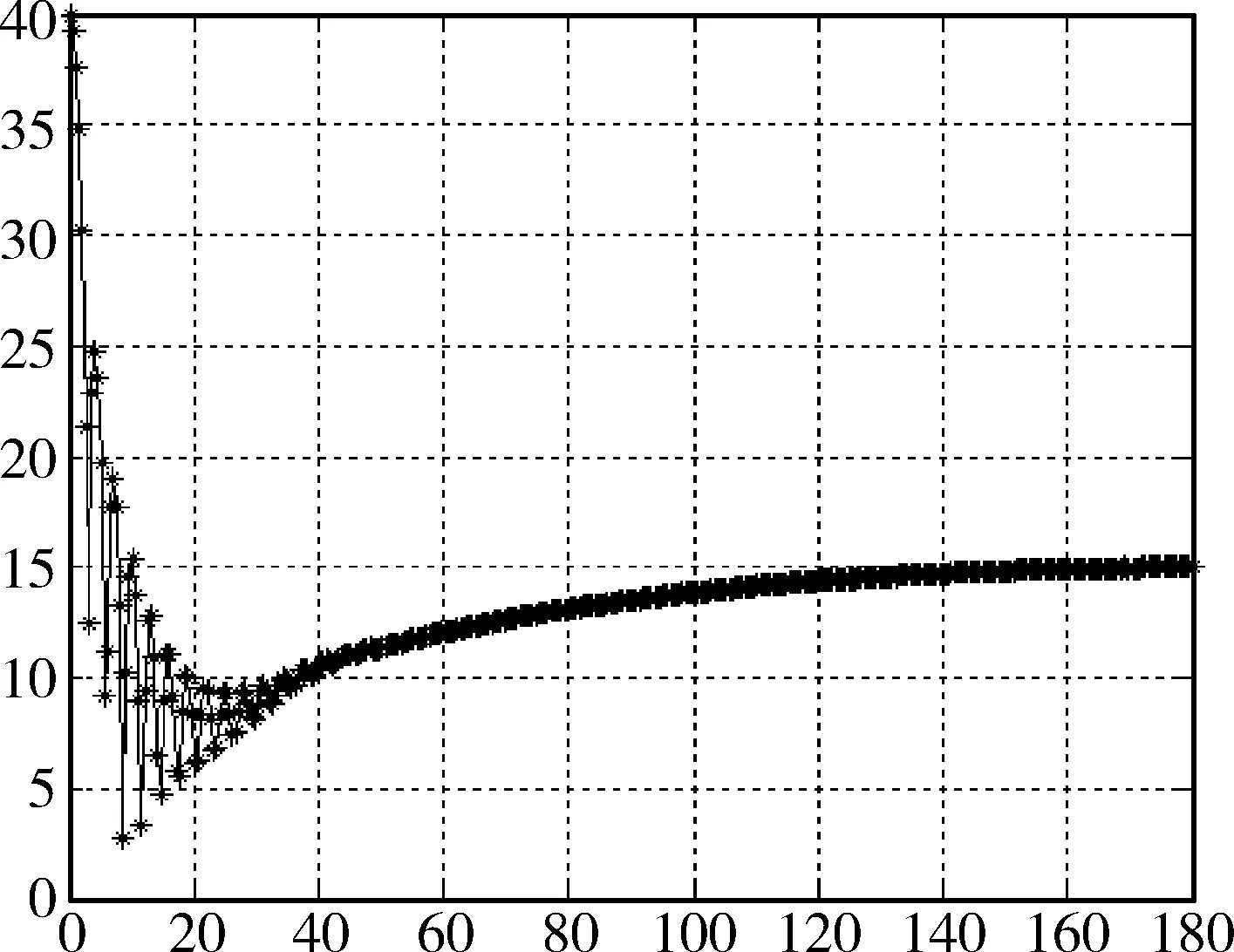
图5 射线追踪法N=1 800外围包围盒半径为10.5λ

3 剖分射线追踪算法的应用

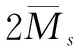
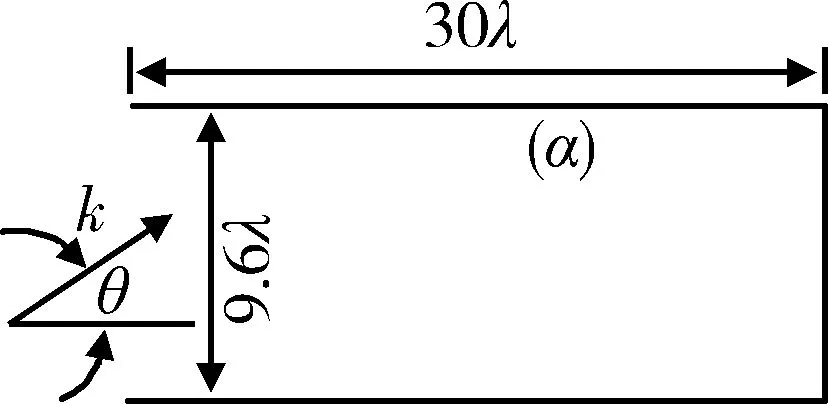
图6 二维矩形腔体

建立上文所述的空间数据结构，并按照图7所示的流程计算电磁散射问题。

图8是基于该射线追踪算法计算的二维电磁散射结果。与文献[10]的结果对比，射线追踪计算的结果一致性良好，单站RCS成对称分布，符合预期。

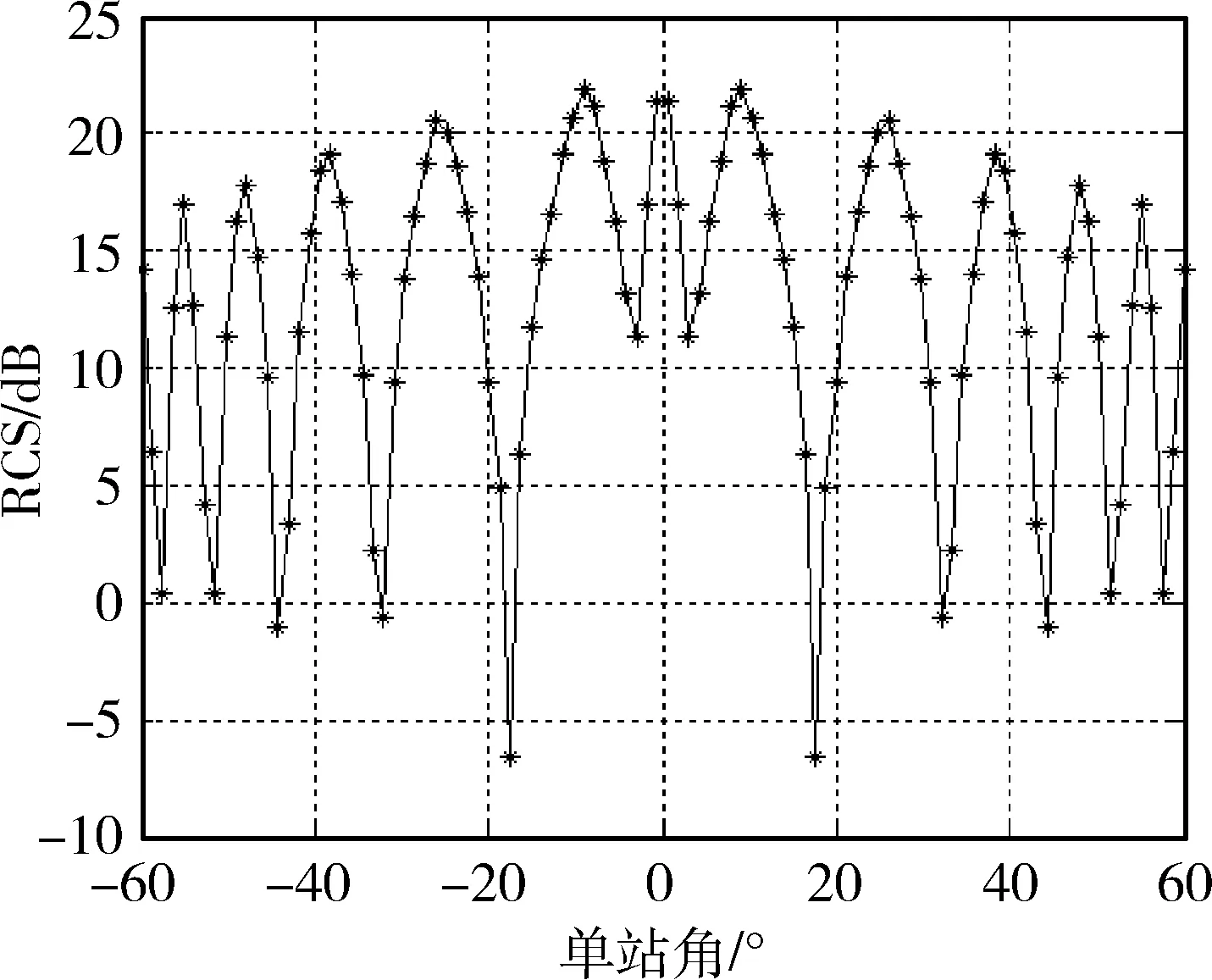
图8 二维矩形腔体的单站RCS

4 结论

本文给出了二维环境下基于空间剖分的射线跟踪法的矢量代数模型，这种方法更便于编程实现且程序运行效率较高。通过计算实例表明，该矢量代数模型能方便准确地进行计算，利用基于空间剖分射线追踪方法找出传播路径。通过实际算法的实现以及结果的对比，较好地解决了在电大尺寸二维物体的散射计算问题，验证了该射线追踪算法的正确性。

[1] 吴志忠.移动通信无线电波传播[M].北京：人民邮电出版社,2002.

[2] 曹伟,徐立勤.电磁场与电磁波理论[M].北京:北京邮电大学出版社,1999.

[3] LUMHOLT M, BREINBJERG O. A new GTD slope diffraction coefficient for plane wave illumination of a wedge[C]. IEEE Society International Symposium on Antennas and Propagation, Los Angeles, CA, USA, 1997:1756-1759.

[4] BERNARDI P, CICCHETTI R, TESTA O. An accurate UTD model for the analysis of complex indoor radio environments in

microwave wlan systems[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(6):1509-1520.

[5] BALDAUF J, LEE S W, JENG S K, et al. High frequency scattering from trihedral corner reflectors and other benchmark targets: SBR versus experiment[J]. IEEE Transactions on Antennas and Propagation, 1991,39(9): 1345-1351.

[6] LING H, CHOU R C, LEE S W. Shooting and bouncing rays: calculating the RCS of an arbitrarily shaped cavity[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(2):194-205.

[7] 张法全,杨晓哲,叶金才. 微震定位系统中拾震器布阵研究[J]. 电子技术应用, 2015, 41(4):148-151.

[8] 李永,王关云,刘芫健. 典型办公室下60GHz毫米波传播特性研究[J]. 微型机与应用, 2016, 35(4):65-67.

[9] 杨会明. 时域信号单纯形射线追踪法的研究[D]. 南京: 南京邮电大学, 2009.

[10] 王树民, 李明之, 王长清. GRE-FDTD混合法对二维矩形终端任意形状进气道RCS的计算[J]. 电子学报, 2000, 28(6):138-141.

Research on ray tracing algorithm based on space subdivision

Li Yueyuan, Xie Lijie, Zheng Yangcheng

(School of Electronic Science & Eyineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)

Conventional ray tracing algorithms need to test the intersection of ray and propagation environment objects, which wastes a lot of time and is not efficient. In this paper, a ray tracing algorithm based on spatial subdivision is proposed. The central idea is establishing the geometric model of the propagation environment, and using the segmentation software (eg Gmsh) to remove the spatial post-partition propagation environment. The geometrical relationship between the ray and the subdivision is determined, and the ray propagation path is determined.

GO; radio propagation geometrical opticsc; ray tracing; space division

TP92

A

10.19358/j.issn.1674- 7720.2017.12.019

李悦园，谢礼节，郑羊城.一种基于空间剖分的射线追踪算法的研究[J].微型机与应用，2017,36(12)：64-67.

2016-12-26)

李悦园(1991-)，男，通信作者，硕士研究生，主要研究方向：高频计算电磁学。E-mail：453180905@qq.com。

谢礼节(1992-),男，硕士研究生，主要研究方向：计算电磁学和圆极化GPS天线。

郑羊城(1991-),男，硕士研究生，主要研究方向：矩量法计算电磁学低频算法。