既有桥梁车辆荷载行进过程数学模型构建

叶际斌

(深圳市市政设计研究院有限公司， 广东 深圳 518028)

既有桥梁车辆荷载行进过程数学模型构建

叶际斌

(深圳市市政设计研究院有限公司， 广东 深圳 518028)

根据我国现有的车辆荷载样本模型，考虑在不同运行状态下车辆荷载出现的统计规律，提出n辆车行进于桥梁上并且连续到达的概率密度函数的通用表达式及解析表达式。解析表达式可避免通用表达式繁琐的数值计算，为确定桥上最大可能车辆数提供便利。

既有桥梁； 车辆荷载； 数值模拟； 截口分布； 卷积积分； 伽马分布

车辆荷载是桥梁结构所承受各种荷载中最重要的一种。车辆荷载的随机性给其预测带来了不确定性。李广慧等[1]通过分析英国交通实验室实测WIM数据，得到多辆卡车同时出现于桥上的概率分布。王磊等[2]利用我国既有的车辆荷载统计数据，采用卷积方法确定了n辆连续到达不同车辆的概率密度函数的一般表达式。本文结合车辆运行状态时间间距的截口概率分布形式，给出了n辆连续到达不同车辆的概率密度函数的解析表达式。同时推导了基于车辆间距的n辆连续到达不同车辆的概率密度函数的一般表达式，实例表明，该计算模型适用于任何跨径的桥梁。

1 车辆荷载概率分布模型

我国“公路桥梁车辆荷载研究”课题组[3]为完善现阶段国内车辆荷载的基础数据，分别在国内具有代表性的4条国道上设置车辆动态测试仪，并于各道路重点采集其中某一主要行车道上交通流的车辆荷载数据。

利用K-S检验法按伽马、极值I型、威布尔、正态和对数正态5种分布类型分别对车辆荷载各数据集(车重、轴重、车间距等)进行分布拟合检验，并由极大似然估计法给出各种分布参数。经分析，可认为公路桥梁车辆荷载的基本分布类型为对数正态分布和伽马分布，如表1。

表1 车辆荷载截口概率分布及其参数

Tab.1 Vehicle loading truncated probability distribution and its parameters

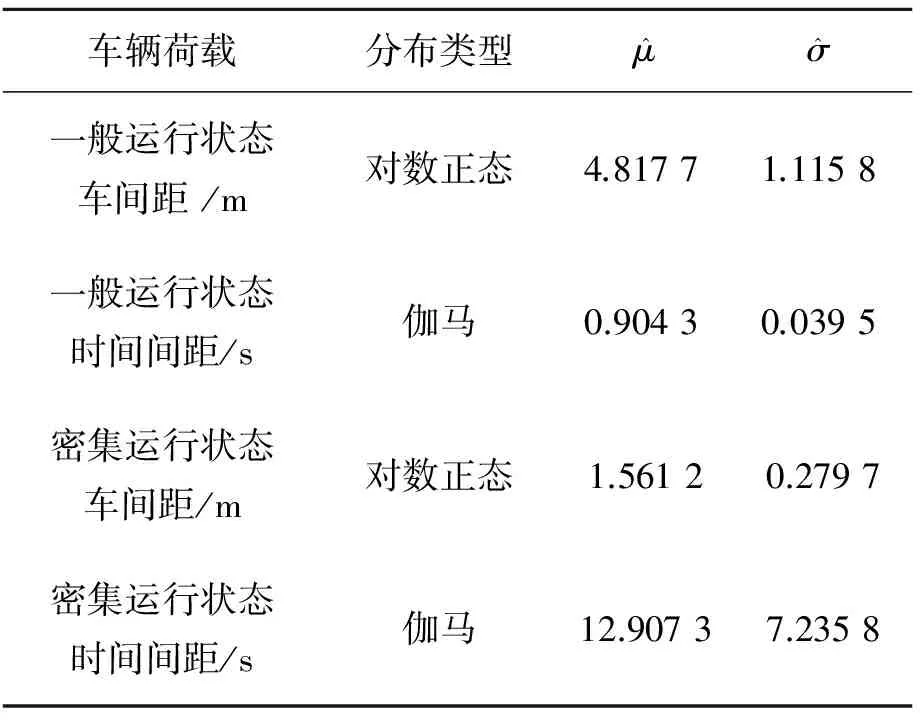
车辆荷载分布类型μ＾σ＾一般运行状态车间距/m对数正态4．81771．1158一般运行状态时间间距/s伽马0．90430．0395密集运行状态车间距/m对数正态1．56120．2797密集运行状态时间间距/s伽马12．90737．2358

2 车辆荷载概率分布函数性质

2.1 对数正态分布

设随机变量X的对数服从均值为μ，标准差为σ的正态分布，则称其服从参数为μ和σ的对数正态分布，即如果X=eY，其中Y～N(μ,σ2)。此时X的概率密度函数为：

(1)

记作X～lnN(μ,σ)，μ和σ分别是lnX的均值和标准差。其分布函数为：

(2)

2.2 伽马分布

设随机变量X的密度函数为式(3)，则称X服从Γ(Gamma)分布，记为X～Γ(α,β)。通常称α为形状参数，β为尺度参数。其分布函数为式(4)。

(3)

(4)

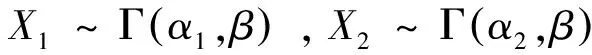
3 车辆进行过程数学模型

3.1 车辆跟车模型

车辆荷载有很强的不确定性，为方便对车辆行进过程数学建模，合理地简化了车辆形式，并且从众多影响车辆荷载模型的参数中选择能较准确描述不同车辆连续到达过程的几个参数，对这些参数时点变化过程进行统计分析，如图1所示。

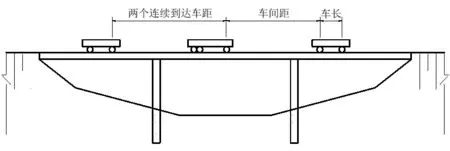
图1 车辆进行过程示意图Fig.1 Vehicles pass a bridge in succession

3.2 基本假设

由于车辆荷载的随机性及复杂性，在推导n辆车连续到达的概率密度函数前，需要做一些合理的假设：

1)桥梁上的车辆为匀速行驶；

2)桥梁上的车辆不发生堵车现象，即认为车辆是按各自要求行驶于桥梁的随机过程；

3)以下讨论均基于单车道，并且认为行驶于某一车道上的车辆不与临近车道发生关系，即单车道的独立性；

4)任意两个连续到达车辆互不影响，即车辆本身相互独立。

基于以上4点假设，便可推导不同连续到达的车辆间距的分布密度函数。

3.3 基于车辆时间间距的数学模型

由表1可知，连续到达的两辆车之间的时间间隔不管是在一般运行状态还是密集运行状态，它们都服从伽马分布，只是分布参数有所不同。

根据假设条件，车速v为定值，因此两连续到达的车辆车间距d=vt，式中t为两车时间间距，服从伽马分布，由伽马分布性质易得两连续到达车辆车间距d的概率密度函数：

(5)

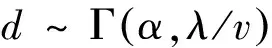
在车辆进行过程模型中，设第1辆车前轴到第3辆车前轴的距离为d3，其概率密度函数可由已知d的概率密度函数通过卷积积分得到：

(6)

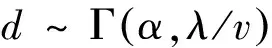
(7)

同理，可设第1辆车前轴至第4辆车前轴的距离为d4，其概率密度函数可由已知的d3及d的概率密度函数通过卷积积分得到：

(8)

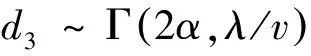
(9)

(10)

同时可得dn概率密度函数的解析表达式：

(11)

以上求得n辆不同连续到达车辆的概率密度函数的解析表达式，利用式(11)容易确定在长为L的桥梁上最大车辆荷载数。

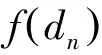
为解决以上不足，本文将推导基于车间距(前车后轴到后车前轴的距离)与车辆长度的车辆荷载连续到达的数学模型。

3.4 基于车辆间距的数学模型

由表1可知，行驶于桥上的车队，连续到达的两辆车之间的车间距l(前车后轴到后车前轴的距离)不管是一般运行状态还是密集运行状态，都服从对数正态分布，对应不同状态分布参数不同：

(12)

根据目前各国关于车长的统计分析，认为车长x服从正态分布，分布参数为μ=4.52，σ2=0.68：

(13)

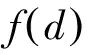
(14)

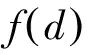
(15)

这样就避免了匀速的假设，并且通过式(15)可计算任意跨度桥梁上行驶的最大车辆数。

4 实例分析

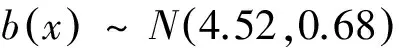
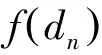
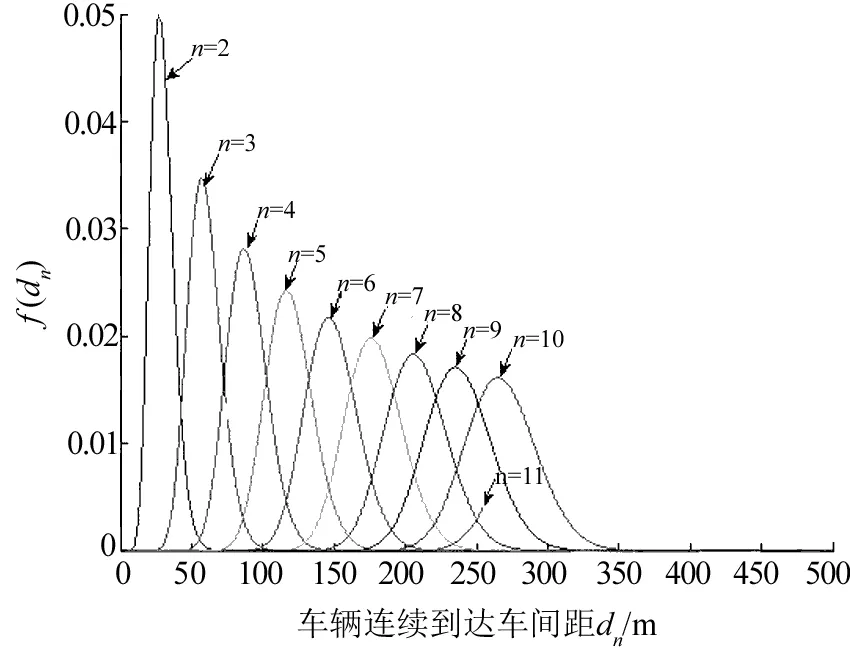
图2 基于时间间距的密集运行状态Fig.2 Intensive running states f(dn)based on time intervals

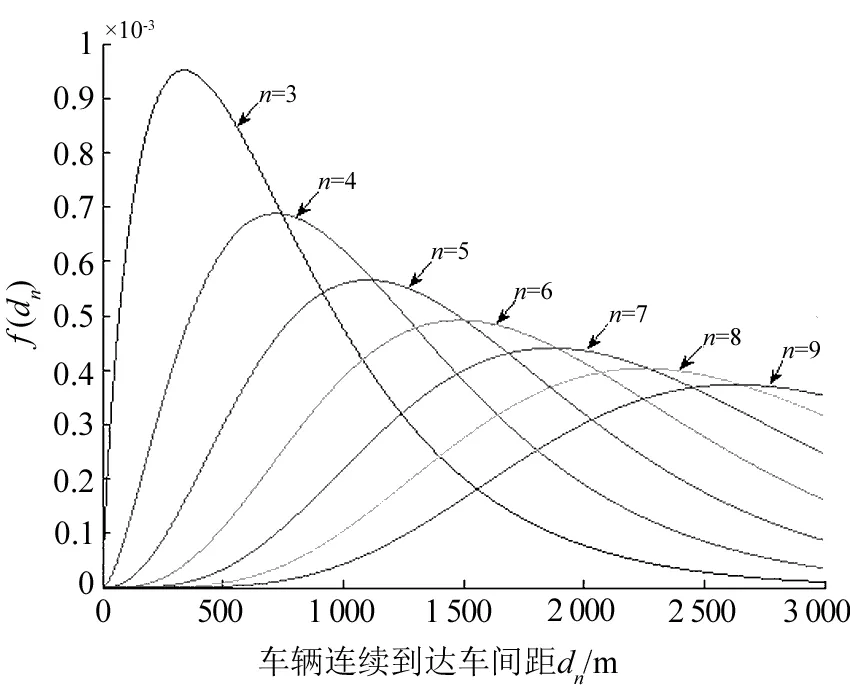
图3 一般运行状态f(dn)Fig.3 General running state

由图2可知，当n=11时，由式(11)计算的概率密度函数图像出现突变，可见当n≥11时，式(11)已不再适用。由图3可知，当n=9时，概率

密度函数图在0～500 m内基本接近于0，由此可判定，一般运行状态时，行驶于该桥上最大可能的车辆数为8。而密集运行状态行驶的最大车辆数可由式(15)计算，本研究只列出部分有代表的连续到达车间分布密度图，如图4。

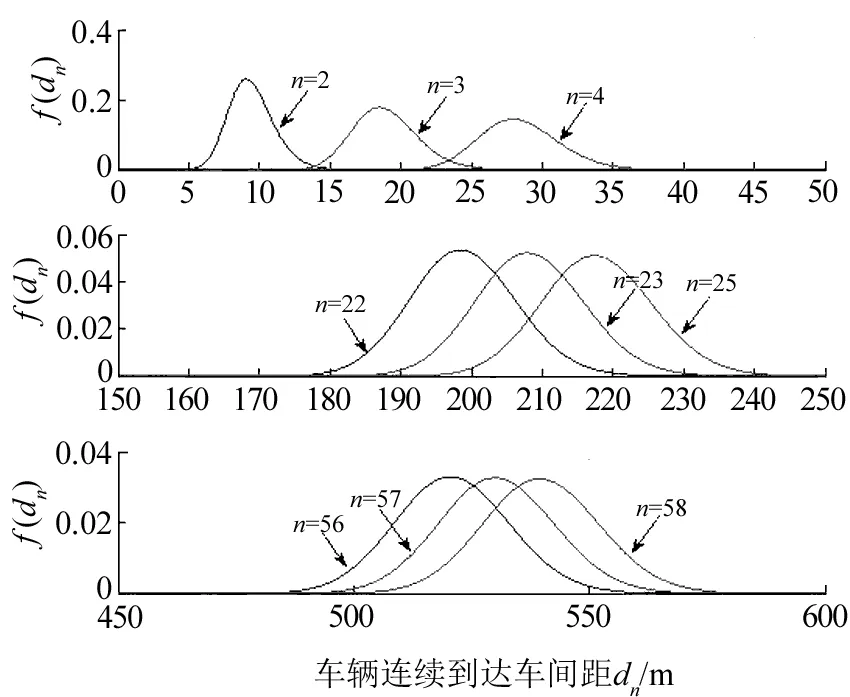
图4 基于车间间距的密集运行状态f(dn)Fig.4 Intensive running states based on vehicular intervals

由图4可知，当n=58时，概率密度函数图在0～500 m基本接近于0，由此可判定，密集运行状态时行驶于该桥上最大可能的车辆数为58。

5 结语

1)推导了基于时间间距的n辆不同连续到达车辆的概率密度函数的解析表达式，避免了一般表达式繁琐的数值计算，为确定桥上最大可能车辆数提供极大便利。

2)经分析，基于时间间距的数学模型只适用于中小跨径桥梁，本文推导了基于车辆间距的n辆不同连续到达车辆的概率密度函数的一般表达式。实例表明，该计算模型适用于任何跨径桥梁。

[1] 李广慧，张存超，王东炜，等.高速公路桥梁活荷载参数研究[J].郑州大学学报，2005，26(1)：20-23.

[2] 王磊，张建仁.既有公路桥梁不同车辆荷载连续到达过程模拟[J].中外公路，2008，28(2)：83-88.

[3] 公路桥梁车辆荷载研究课题组.公路桥梁车辆荷载研究[J].公路，1997(3)：8-12.

[4] 梅刚，秦权，林道锦.公路桥梁车辆荷载的双峰分布概率模型[J].清华大学学报(自然科学版)，2003，43(10)：1394-1396.

[5] 元宇，金红亮.Rice公式外推桥梁荷载效应[J].上海公路，2012 (1)：36-40.

[6] 杨飞.基于实测数据与CA交通流模型的桥梁汽车荷载研究[D].西安：长安大学，2014.

[7] 杨泽刚.典型高速公路实际运行车辆荷载模型研究[D].南京：东南大学，2015.

(责任编辑： 陈雯)

Construction of mathematical model for vehicles’ loaded passing existing bridge

Ye Jibin

(Shenzhen Municipal Design & Research Institute Co., Ltd, Shenzhen 518028，China)

Utilizing available vehicle load sample model in China and the statistical law of vehicle load under different operation conditions, a general expression and an analytical expression of the probability density function of the vehicles passing in succession on the bridge were presented. The simulation results indicate that the analytical expression can avoid the cumbersome numerical calculation of the general expression, and provides great convenience for determining the maximum possible number of the vehicles passing the bridge.

existing bridge； vehicular load； numerical simulation； truncated distribution； convolution integral； gamma distribution

10.3969/j.issn.1672-4348.2017.03.003

2017-03-27

福建省教育厅科技项目(JA10046)

叶际斌(1985-)，男，福建南平人，工程师，硕士，研究方向：车-桥耦合作用。

U441.2

A

1672-4348(2017)03-0215-04