2013—2015年新加坡小学毕业离校考试数学试卷分析
◇江春莲 巩子坤 刘付茵
2013—2015年新加坡小学毕业离校考试数学试卷分析
◇江春莲 巩子坤 刘付茵

近20年来,新加坡学生参加国际数学比较教育研究都取得了很好的成绩,如在2016年公布的国际数学与科学趋势研究(Trends in International MathematicsandScienceStudy,简写为TIMSS)和国际学生评估项目(Program for International Student Assessment,简写为PISA)中,新加坡均以绝对优势排在首位。本世纪初,以美国为代表的西方国家甚至直接引进新加坡的数学教材。新加坡的教育体系最重要的特点是分层教育,从小学五年级起,学生就被分流,学习不同水平的课程,分层的依据是学生的学业成绩。四年级结束时的分流考试只是让那些学习一般水平课程比较吃力的学生学习更基础水平的课程。小学毕业离校考试(Primary School Leaving Examination,简写为 PSLE)则直接决定了学生就读的中学、学习的课程水平和未来发展,所以竞争比较激烈。江春莲和许俊丹曾在2014年翻译介绍过新加坡的PSLE试题,这次我们将对2013—2015年3年间PSLE数学试卷做更详细的分析,并结合我国现今正在进行的数学课程改革提出一些建议。
一、试卷结构
新加坡2013—2015年的PSLE数学试卷结构稳定,都是由两个测试组成,即测试一和测试二。测试一由15道选择题和15道填空题组成,两种题型都是前10道题每题1分,后5道题每题2分,总分40分,测试时间50分钟。测试二由5道填空题和13道解答题组成,填空题每题2分,解答题每题3~5分不等,总分60分,测试时间100分钟。
二、内容分配
我们按照学习内容领域将所有题目分成了四类,即数与运算、代数、几何与测量、数据分析与概率,并将2013—2015年每年各类问题所带的分值加在一起(如表1)。不难发现,新加坡PSLE数学试题以数与运算为主,其分值均占到了60%及以上;其次是几何与测量,其分值约占30%;比较少的是代数(2%~4%)和数据分析与概率(3%)。自2001年以来,我国在新课程中增加了较多数据分析与概率的内容,但新加坡没有在这方面做更多的努力。

表1 新加坡PSLE数学试卷中各内容领域问题所带的分值情况
三、试题特点
1.内容涵盖范围广。
新加坡PSLE数学试卷题目数量多,可以涵盖的领域比较广,从简单的数的计算(如2015年测试一第 16题:求 8020÷5的值)、数的比较(如2015年测试一第12题:将距离3.15 km 、、 3 km105 m按从短到长的顺序进行排列)、分数与小数的四则运算(如 2014年测试一第 17题:求的值),到实际应用问题(如 2015年测试二第9题:一场音乐会的门票,55%是按全价卖的,40%是按半价卖的,余下的20张是免费送出去的。如果门票总共卖了7200元,问门票的全价是多少)等都有。学生不仅需要掌握数学的基本概念,还需要熟悉各种不同情境下的应用。
2.关注数学在实际生活中的应用。
新加坡PSLE测试题中常常出现生活中的应用问题,如下面的阶梯计价问题。
(2015年测试一第27题)表2显示的是一家清洁公司的收费标准:
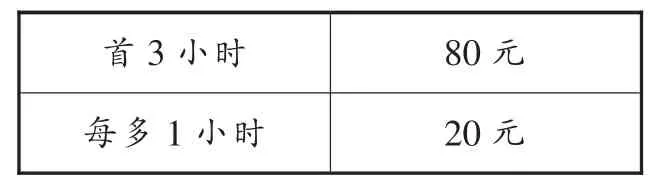
表2
梅农女士付了200元给清洁公司,问:她付了多少小时的费用?
3.问题的复杂程度较高。
作为一种选拔性的考试,新加坡PSLE数学试卷的难度很大。关于数的问题,常常围绕较难的分数、比和比例、效率等概念命制;关于几何的问题,则常常是几个不同图形的组合,难度自然较大。下面我们以2个涉及数的问题和2个几何问题说明其复杂程度。
数的问题1:(2015年测试二第16题)佩怡和家妹买了一些植物,植物的价格如图1所示。
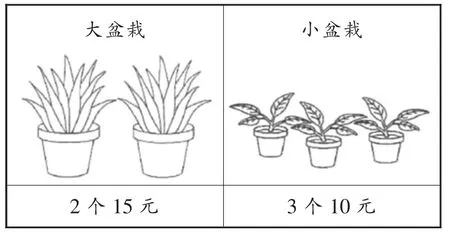
图1
(1)佩怡买了同样盆数的大盆栽和小盆栽,但她花在大盆栽上的钱比花在小盆栽上的多175元,问:她一共买了多少个盆栽?
(2)家妹花在大盆栽和小盆栽上的钱一样多,问:她买的植物中的几分之几是大盆栽?
简答:(1)大盆栽 6个 45元,小盆栽6个 20元,相差25元,175元的价格差是25元的7倍,所以佩怡一共买了(6+6)×7=84(个)盆栽。
(2)30元可以买4个大盆栽或9个小盆栽,所以家妹买的植物中大盆栽占。
数的问题2:(2014年测试二第13题)林先生有长、短尺子共540个。当他卖掉相同数目的两种尺子后,长尺子剩下,短尺子剩下,问:他一共剩下多少个尺子?

几何问题2:(2015年测试二第11题)如图3,在一个长28m的长方形花园里,有一条宽2m的步道。步道由以W为圆心的四分之一圆环、以Z为圆心的半圆环和直线段组成,WX=YZ。子,所以还剩540-200×2=140(个)尺子。
几何问题1:(2015年测试二第6题)如图2,四边形CDEF是一个平行四边形,A、F、C在一条直线上,B、F、E在一条直线上,且BA=BC,∠ABF= 30°,∠DEF=54°。
(1)求∠EFC;
(2)求∠FBC。

图3
(1)求长方形花园的宽;
(2)求步道的面积。(π取3.14)
四、启示
在《义务教育数学课程标准(2011年版)》(以下简称《课标(2011)》)中,特别强调要培养学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。如何检测呢?新加坡PSLE试题提供了一些参考。
1.对数感的考查。
《课标(2011)》把数感定义为关于数与数量、数量关系、运算结果估计等方面的感悟。建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系。良好的数感可以体现在很多方面,如能大致估计一段路线的长度、一个物体的质量、一个平面图形的面积等。新加坡PSLE试题在这方面有很好的尝试。
(2015年测试一第6题)8个1元新加坡硬币的总质量大约是多少?
①6克 ②60克 ③600克 ④6000克
(2015年测试一第10和11题)请根据如下的信息回答问题(1)和问题(2)。
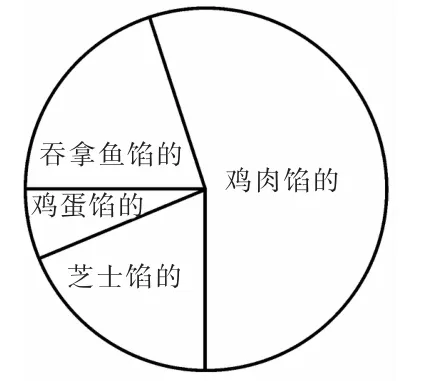
图4
(1)哪个分数是鸡肉三明治的?

(2)哪个分数是鸡蛋三明治的?

2.对符号意识的考查。
由前面对PSLE试题内容的分析可以看出,在新加坡的小学数学课程中,代数的内容较少,所以对符号意识的考查仅限于用字母表示数量关系和给定字母的值后求某个含该字母的表达式的值。
(2015年测试一第4题)已知g=6,求9g-4+2g的值。
3.对空间观念的考查。
《课标(2011)》认为:空间观念主要是指根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形等。新加坡PSLE数学测试题,比较关注二维平面上的东南西北方位。
(2015年测试一第9题)如图5所示,图中表示出了一个旗杆在场地ABCD中的位置。问:该场地的哪个角落在旗杆的东南方向?
①A ②B ③C ④D

图5
4.对几何直观的考查。
《课标(2011)》认为:几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。我们认为几何直观主要指能根据所作的较准确的几何图形判断图形的特殊性质,如判断两直线之间的平行、垂直关系,或判断角的相对大小等。下面给出新加坡PSLE试题中的三个例子。
(2015年测试一第2题)图6中标出了6个角,其中有多少个比直角大?
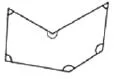
图6
(2015年测试一第20题)如图7,在一个方格图中显示了地图上的五条线路。
(1)说说哪两条线路互相平行。
(2)说说哪两条线路互相垂直。

图7
(2014年测试一第20题)图8由一些完全一样的三角形组成,其中四个被涂上了阴影。请再将两个三角形涂上阴影,使得直线XY成为该图形的对称轴。
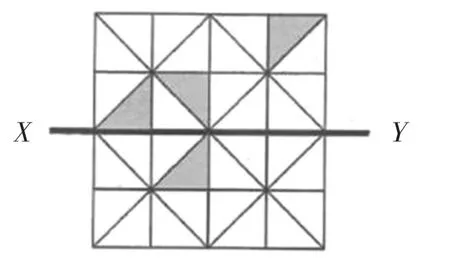
图8
5.对数据分析观念的考查。
尽管数据分析与概率在新加坡小学数学课程中所占比重不大,但每一年的PSLE数学试卷都有一道大题是与统计相关的,而且是以统计图呈现数据的,学生需要仔细观察统计图,理解统计图中的数量关系。
(2014年测试二第6题)下面的条形图(如图9)表示一家商店卖出的四种文件夹的数量,表3给出了这些文件夹的单价。
(1)压夹文件夹的数量占卖出的文件夹总数量的几分之几?写成最简分数形式;
(2)在已售出的这四种文件夹中,哪种文件夹卖得的钱数最多?最多是多少?

图9
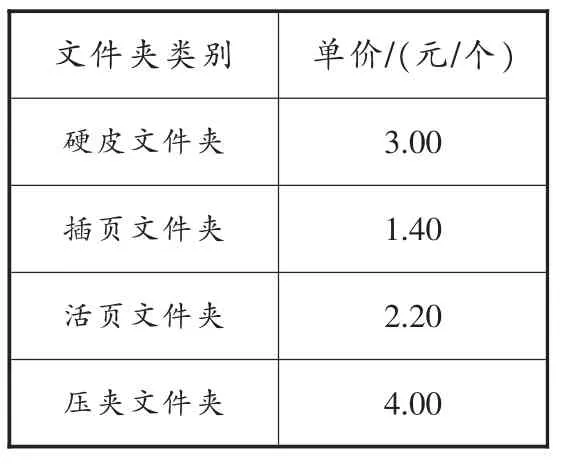
表3
6.对运算能力的考查。
运算能力的培养是小学数学课程的核心,学生不仅要学习整数、分数、小数的四则运算,还需要计算速度、灵活性等,因为这些是解决几乎所有数学问题都需要的能力。纵观PSLE数学试卷,我们发觉新加坡对学生运算能力的要求不高,在回答测试二试题的时候还可以使用计算器。
7.对推理能力的考查。
新加坡PSLE数学测试对数学推理能力的要求比较高,很多时候需要进行转换,如下面一个关于钱的问题。
(2015年测试二第17题)三个女孩艾米、贝丝和辛迪有一样多数目的硬币。艾米和贝丝既有50分的,也有10分的,艾米有9个10分的,贝丝有15个10分的,辛迪只有50分的。
(1)在这三个女孩中,谁的钱数最多?谁的最少?
(2)艾米和贝丝的总钱数相差多少?
(3)贝丝用她所有的50分硬币买了一些食物后,她就比辛迪少10元钱,问:辛迪有多少个50分硬币?
分析:我们可以将三个女孩的硬币数目及钱数列成表4[设每个女孩的硬币总数目都是(24+n)]。

表4
由表4不难发现,在硬币总数目一样的情况下,拥有50分硬币越多的女孩,其钱数越多,所以辛迪的钱数最多,贝丝的钱数最少。艾米拥有的10分硬币比贝丝少6个,则她拥有的50分硬币就应该比贝丝多6个,所以艾米比贝丝多50×6-10×6=240(分)。同理,贝丝比辛迪少 50×15-10×15=600(分)=6(元)。当贝丝花完全部的50分硬币后,她就比辛迪少10元,也就是说,贝丝的50分硬币只有4元钱,即贝丝只有8个50分硬币,所以n=-1,所以辛迪有23个50分硬币。
8.对模型思想的考查。
近年来,模型思想得到数学教育界的充分重视,各国也纷纷在数学课程标准中加进数学建模的内容,新加坡是在2012年的新课程中明确加入数学建模的内容的。因为方程、不等式、函数等不是新加坡小学数学课程的内容,所以新加坡PSLE数学试卷主要通过一类找规律的问题考查学生的数学建模能力,如下面的一个图形变化规律的题目。
(2015年测试一第30题)孟云想要用棱长为1cm的小方块搭建台阶,图10显示了他已搭建的台阶,分别有2cm、3cm和4cm高。如果孟云一直这样搭下去,当用了140个方块时,他搭的台阶有多高?
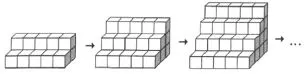
图10
对新加坡学生来说,要解决这样的问题,不需要建立任何代数式和方程,而只需列出表格,观察其中方块数的变化规律。
从上面的问题可以看出,新加坡PSLE试题不仅有很丰富的背景情境,而且很强调解题策略。PSLE试题中有些问题的背景和PISA的很像,这也是新加坡在近20年来致力于提高学生数学问题解决能力和数学建模能力的一个体现。在新加坡的小学和初中的教学大纲上均列出了约12条可以引导学生思考问题的解题策略。江春莲的博士论文研究发现,尽管新加坡学生在其设计的速度问题测试中的表现不及中国学生,但新加坡学生多种解题方法的成功使用使得新加坡学生在个别问题上的表现优于中国学生,而这些解决问题的策略可以很好地帮助那些在数学学习上有困难的学生更好地理解问题,进而找到问题的解答方法。
我国基础教育数学课程改革中,课程标准、教材进行了较大的改革,一线教学也发生了很好的变化,但是,评价改革严重滞后:是否进行学业水平测试,如何进行选拔性测试,选拔性测试如何命题,如何在保证教育公平性的前提下促进优秀学生的发展,等等,这些问题,值得我们好好思考。新加坡的PSLE数学测试,也许会给我们提供一些有益的借鉴。
[1]Mullis I.V.S.,Martin M.O.,Foy P.&Hooper M..TIMSS 2015 International Results in Mathematics[DB/OL].http∶//timssandpirls.bc.edu/timss2015/international-results/.
[2]OECD.PISA 2015 results(Volume1):Excellence and Equity in Education,PISA,OECD Publishing,Paris[DB/OL].http∶//dx.doi.org/10.1787/9789264266490-en.
[3]江春莲,许俊丹.新加坡小学毕业考试数学试卷[J].小学教学(数学版),2014(2).
[4]江春莲.数学问题解决——中新两国学生解决速度文字题的策略和错误[M].北京:科学出版社,2016.
(作者单位:澳门大学教育学院,杭州师范大学理学院,澳门大学教育学院)

