多边形骨料混凝土弹性模量预测的数值方法

周欣竹，钱梦必，郑建军

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

多边形骨料混凝土弹性模量预测的数值方法

周欣竹1,2，钱梦必1，郑建军1,2

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014；2.浙江省工程结构与防灾减灾技术研究重点实验室，浙江 杭州 310014)

混凝土在建筑、水利、海洋和道路工程中应用广泛，其弹性模量是结构变形计算的关键参数.将混凝土细观结构模拟与快速傅里叶变换相结合，提出了混凝土弹性模量预测的数值方法.考虑周期性边界条件给出了多边形骨料和界面在水泥石基体中的随机分布模拟方法.利用快速傅里叶变换方法给出了三相混凝土在外荷载作用下的平均应力、平均应变和弹性模量.将数值方法与文献中的试验数据进行比较，结果表明：当骨料面积百分数分别为40%，60%时，它们之间的相对误差小于5%，初步验证了该数值方法的有效性.基于数值结果，量化了界面弹性模量和厚度对混凝土弹性模量的影响，发现提高界面弹性模量或减小界面厚度都可以有效提高混凝土弹性模量.

混凝土；弹性模量；快速傅里叶变换；多边形骨料；界面层

混凝土作为一种建筑材料，由于其良好的抗水性、可模性和成本低等优点被广泛应用，弹性模量是结构变形计算的关键参数.近年来，随着计算机技术的飞速发展，对混凝土弹性模量的研究不再局限于试验，国内外学者将越来越多的目光投向细观力学模拟[1].相比于试验方法，细观力学模拟有其独特的优越性，不受试验环境、试验周期和试件尺寸的影响，并可获得与材料内部细观结构之间的定量关系，为混凝土宏观性能的优化设计提供理论依据.串联模型、并联模型、混合律模型以及Hirsch模型都是弹性模量预测的传统模型，在这些模型中，混凝土通常被模拟成两相复合材料，相对误差较大.为了更精确地预测混凝土弹性模量，国内外学者提出其他一些方法，其中比较典型的是自洽法[2]、广义自洽法[3]、稀疏分布模型[4]和Mori-Tanaka法[5]等.早在1999年，Li等就提出了四相球模型，但是该模型忽略了界面重叠，导致界面的体积百分数大于实际值[6].近年来，针对含有界面这一特殊结构的混凝土，郑建军等提出弹性模量预测的三相格构模型[7]，在此基础上，甘祎毓等进一步考虑骨料形状效应[8]，提出了改进的三相格构模型.此外，Zheng等基于三相复合圆模型提出了混凝土弹性模量的估计方法[9]，应宗权等利用细观力学均匀化方法，预测不同形状骨料混凝土的弹性模量[10].

在以往的研究中，通常将混凝土中的骨料模拟成圆形或椭圆形，与实际工程中的碎石骨料存在一定差异，虽然应宗权[10]等将骨料模拟成多边形，但是忽略了界面层的存在.另外，大多数预测方法均涉及到有限元法，该方法不仅在界面网格划分时存在困难，而且总刚度方程的求解需要大量的时间，对计算机性能的要求较高.因此，笔者在前人工作的基础上，首先模拟水泥石基体中的多边形骨料分布，并考虑界面层的影响，然后应用快速傅里叶变换法给出混凝土弹性模量，该方法的有效性初步为试验结果所证实.

1 多边形骨料随机分布模拟

1.1 骨料生成

混凝土是一种典型的非均质材料，在细观水平上，它是由骨料、水泥石基体和界面组成的三相复合材料.在实际工程中，骨料往往采用碎石，在混凝土构件的截面上呈现多边形.在极坐标系中，多边形骨料的形状可以通过边数、极半径和极角来确定.根据王宗敏等提出的多边形骨料表示方法[11]，借助Monte-Carlo抽样原理，可以生成各种大小和形状的多边形骨料.通过矢量叉乘法判断生成的多边形是否存在凹点，如果存在凹点，直接连接与凹点相邻的两点对多边形骨料进行修正.该方法的优点之一是可以按照骨料级配要求生成各种粒径和长细比的骨料[12-13].

1.2 骨料分布

按照级配要求生成各种尺寸的多边形骨料后，就可以将骨料逐一随机分布到混凝土中.在模拟时选用边长为a的正方形作为模拟区域，在分布每一颗骨料时不仅需要判断它是否与已经分布的骨料重叠，而且为了消除边壁效应，需要引入骨料分布的周期性边界条件[14].大量的实验表明：骨料粒径对界面层厚度几乎没有影响，普通混凝土的界面层厚度h一般在0.01～0.05 mm之间.因此，只要在每颗骨料的周边加上厚度为h的界面层就可获得界面结构.

取模拟区域边长a=150 mm，骨料粒径为5～20 mm，骨料边数为4～10，骨料面积百分数Aa分别取40%，60%，利用笔者自编的骨料分布程序即可获得混凝土中二维骨料随机分布，结果如图1所示.从图1可以看出：模拟所得的骨料分布与实际混凝土截面上的骨料分布非常相似.

图1 不同骨料面积百分数的骨料分布模拟Fig.1 Simulation of aggregate distribution with different aggregate area fractions

2 混凝土弹性模量预测的FFT法

2.1 基本方程

对于非均质混凝土，假设点(x1,x2)处的弹性张量Cijkl(x1,x2)是坐标(x1,x2)的函数，则混凝土的应力—应变关系可以表示为

(1)

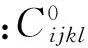
(2)

式(2)的一般解[15]可表示为

εij=-Γijkl(x1,x2)×τkl(x1,x2)

(3)

式中：Γijkl为周期格林张量；符号“×”表示卷积.对式(3)进行傅里叶变换有

(4)

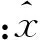
(5)

式中：λ0，μ0分别为拉梅常数.

2.2 迭代步骤

基于上述基本原理，二维非均质混凝土的弹性模量可以按照以下迭代步骤进行预测：

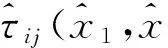
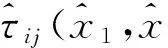
4) 根据应力—应变公式求得第i+1次迭代的应力.

迭代收敛以前后两次迭代值的相对误差小于允许值为标准，当迭代收敛后，对各像素点的应力和应变分别进行加权计算，最后得到非均质材料的弹性模量.根据多次分析，运算收敛最快时拉梅常数[15]满足的条件为

(6)

(7)

2.3 具体步骤

基于数值模拟所得到的多边形骨料混凝土模型，应用前两节所述的基本原理和迭代方法预测混凝土弹性模量，具体步骤如下：

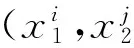
3) 应用上节所述的迭代步骤预测混凝土弹性模量Ec.

在具体计算中，取K=8，当前后两次迭代值的相对误差小于0.001时，停止迭代.

图2 像素点的选取Fig.2 Selection of pixel points

3 试验初步验证与影响因素分析

选择Stock等的试验数据来初步验证笔者数值方法的有效性[16].在该试验中，水泥石基体和骨料的弹性模量分别为11.6，74.5 GPa，骨料的最大直径为19 mm，骨料面积百分数分别为20%，40%，60%.根据前人的研究成果，其他参数[9,17]选取如下：界面层厚度h=0.03 mm，界面弹性模量为水泥石基体弹性模量的0.4倍，即Ei=0.4Ep，界面层、水泥石基体和骨料的泊松比分别为0.35，0.25，0.15.根据这些参数，应用上面所提出的数值模拟方法预测混凝土弹性模量，结果如图3所示，从图3可以看出：当骨料面积百分数为20%时，两者之间的相对误差较大，其值为18.63%，这可能是由于骨料面积百分数低，试验时骨料分布不均匀，水分容易蒸发，导致试验结果偏大，但实际混凝土的骨料面积百分数远高于20%.当骨料面积百分数为40%，60%时，两者之间的相对误差分别为3.84%，0.24%，因此，该数值方法的有效性得到了试验的初步验证.

界面是混凝土中最薄弱的环节，对混凝土弹性模量的影响主要体现在界面弹性模量和厚度两个方面，为此，在下面的影响因素分析中，除了界面弹性模量和厚度外，其他参数均与上述试验验证所用的参数相同.首先假设界面厚度为h=0.03 mm，界面弹性模量分别为水泥石基体弹性模量的0.2，0.4，0.6倍，计算结果如图4所示.从图4中可以看出：当骨料面积百分数一定时，界面弹性模量越大，混凝土弹性模量也越大，当骨料面积百分数为60%时，Ei=0.6Ep的混凝土弹性模量比Ei=0.2Ep的混凝土弹性模量大11.87%，这是因为界面弹性模量越大，骨料与水泥石基体之间的粘结力越强，混凝土弹性模量越大.其次，假设界面弹性模量Ei=0.4Ep，界面厚度分别为0.01，0.03，0.05 mm，计算结果如图5所示.从图5可以看出：当骨料面积百分数一定时，界面厚度越大，混凝土弹性模量反而越小，当骨料面积百分数为60%时，h=0.01 mm的混凝土弹性模量比h=0.05 mm的混凝土弹性模量大7.63%，这是因为界面厚度越大，界面面积百分数越大，混凝土弹性模量越小.

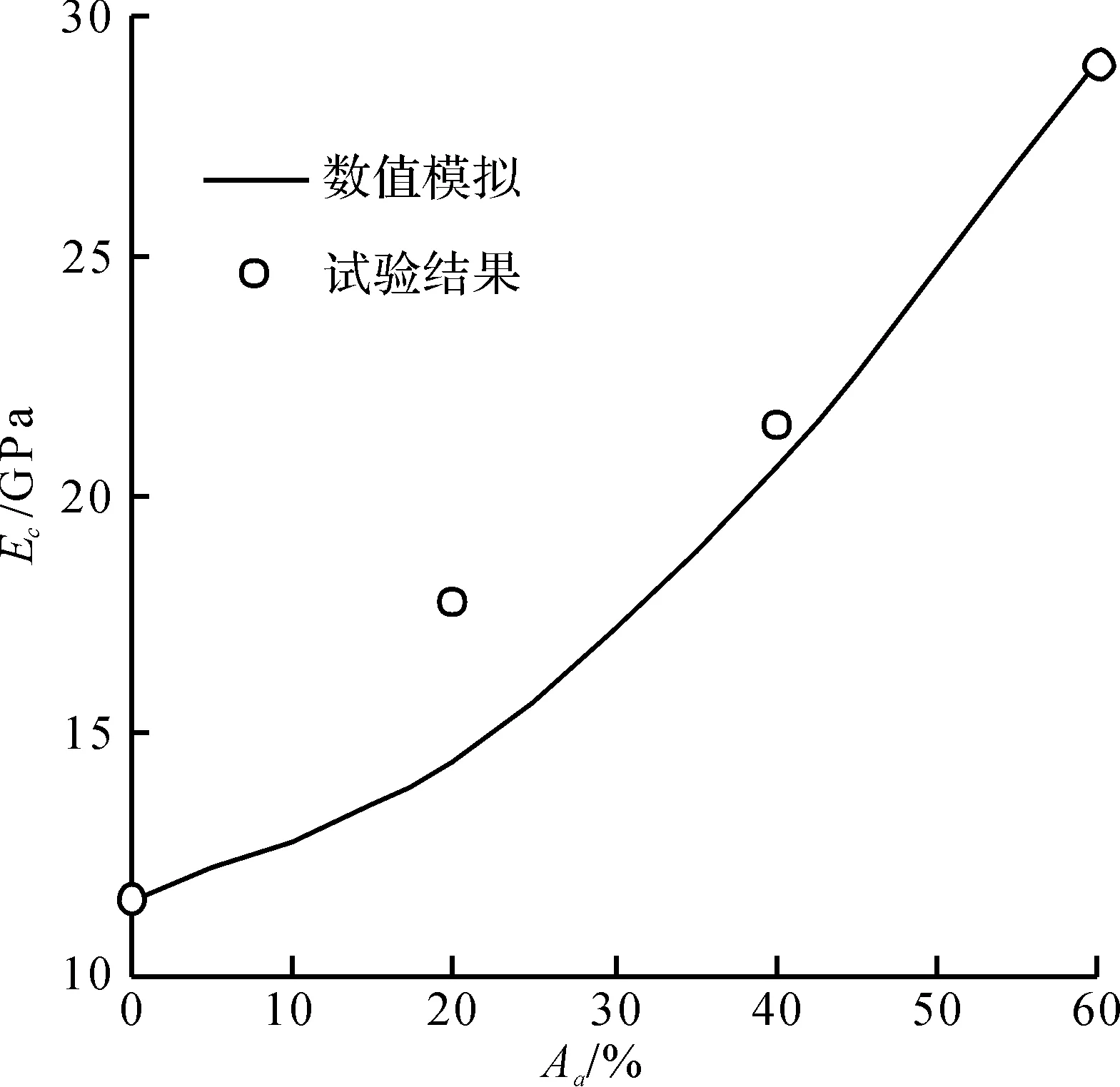
图3 数值结果与Stock等试验结果的比较Fig.3 Comparison between numerical results and experimental results of Stock et al

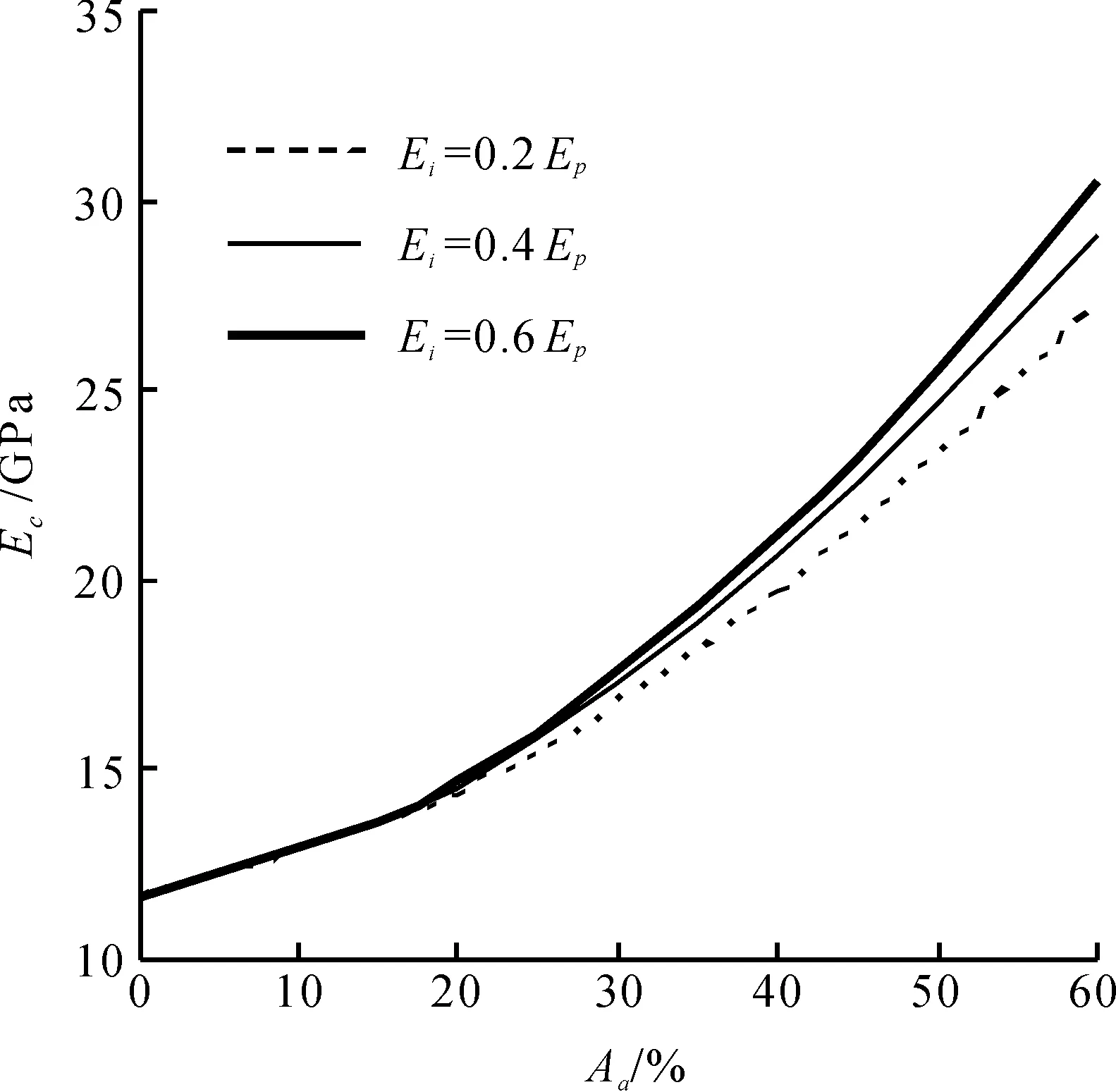
图4 界面弹性模量对混凝土弹性模量的影响Fig.4 Effect of elastic modulus of ITZ on elastic modulus of concrete

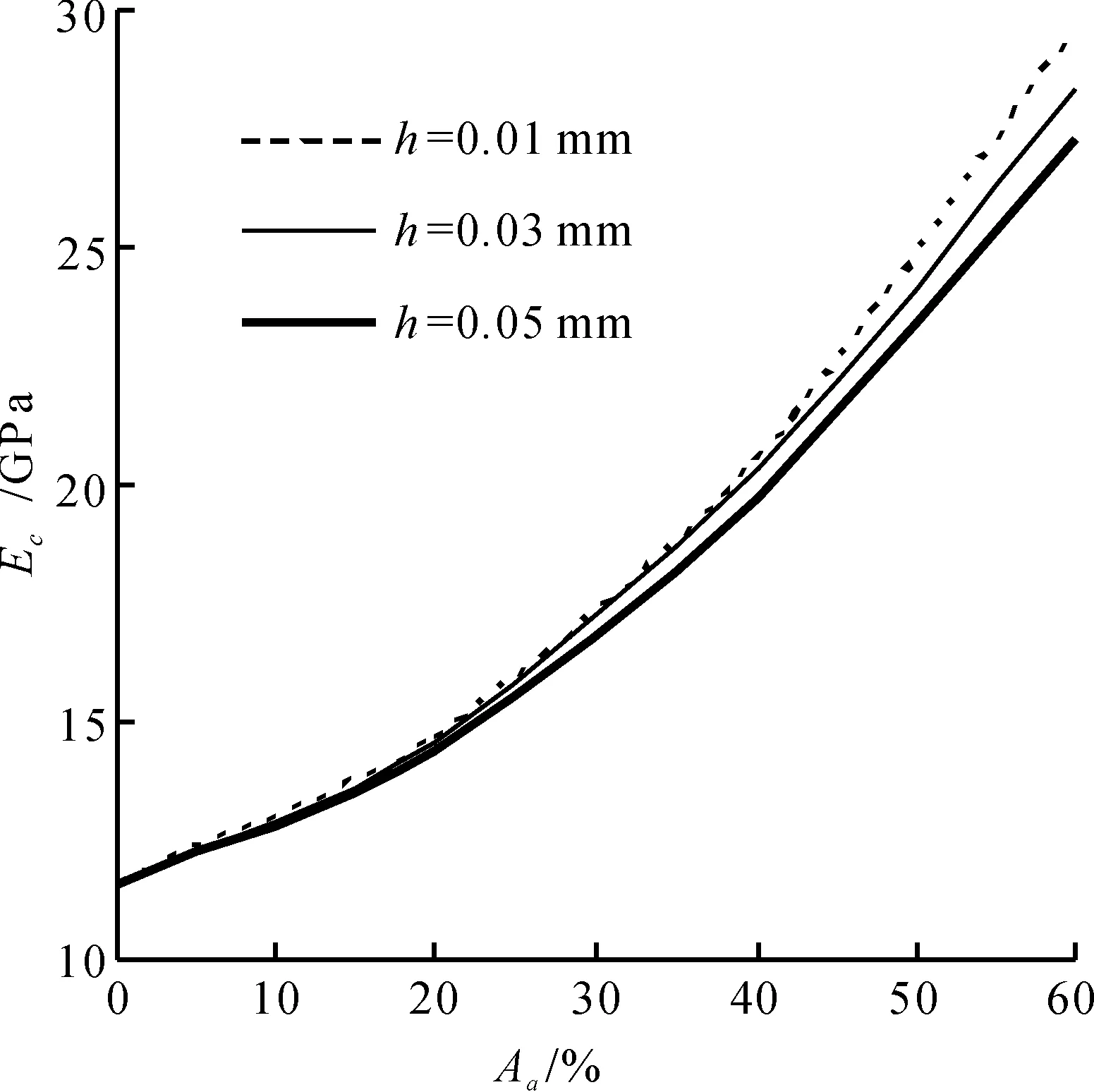
图5 界面厚度对混凝土弹性模量的影响Fig.5 Effect of ITZ thickness on elastic modulus of concrete

4 结 论

提出了多边形骨料混凝土弹性模量预测的数值方法.在考虑周期性边界条件的情况下给出了混凝土中多边形骨料和界面在混凝土截面中的随机分布方法，更符合实际混凝土.基于快速傅里叶变换和反变换技术提出了预测三相混凝土弹性模量的具体步骤和数值方法.在该方法的有效性得到初步验证的基础上进一步讨论了界面弹性模量和厚度对混凝土弹性模量的影响，发现增大界面弹性模量或减小界面厚度都能有效地增大混凝土弹性模量，当骨料面积百分数为60%时，Ei=0.6Ep的混凝土弹性模量比Ei=0.2Ep的混凝土弹性模量大11.87%，h=0.01 mm的混凝土弹性模量比h=0.05 mm的混凝土弹性模量大7.63%.

[1] 郑建军,周欣竹,邢鸿燕.二维圆形骨料分布的边界效应及简单应用[J].浙江工业大学学报,2003,31(1):7-11.

[2] KRÖNER E. Berechnung der elastischen konstanten des vielkrials aus den konstanten des einkristalls[J]. Zeitschrift für physik a hadrons and nuclei,1958(151):504-518.

[3] CHRISTENSEN R M, LO K H. Solution for effective shear properties in a three phase sphere and cylinder models[J]. Journal of the mechanics and physics of solids,1979,27(4):315-330.

[4] 何巨海,张子明,艾亿谋,等.基于细观力学的混凝土有效弹性性能预测[J].河海大学学报(自然科学版),2008,36(6):801-805.

[5] MORI T, TANAKA K. Average stress in matrix and average of materials with misfitting inclusions[J]. Acta metallurgica,1973,21:571-574.

[6] LI Guoqiang, ZHAO Yi, PANG S S. Four-phase sphere modelling of effective bulk modulus of concrete[J]. Cement and concrete research,1999,29(6):839-845.

[7] 郑建军,周欣竹.用于混凝土弹性模量预测的三相格构模型[J].建筑材料学报,2004,7(2):133-137.

[8] 甘祎毓,郑建军,周欣竹,等.椭圆形骨料混凝土弹性模量预测的格构模型[J].甘肃水利水电技术,2012,48(2):22-24.

[9] ZHENG Jianjun, LI Chunqing, ZHOU Xinzhu. An analytical method for prediction of the elastic modulus of concrete[J]. Magazine of concrete research,2006,58(10):665-673.

[10] 应宗权,杜成斌,孙立国.基于随机骨料数字模型的混凝土弹性模量预测[J].水利学报,2007,38(8):933-937.

[11] WANG Z M, KWAN A K H, CHAN H C. Mesoscopic study of concrete I: generation of random aggregate structure and finite element mesh[J]. Computers and structures,1999,70(5):533-544.

[12] 张剑,金南国,金贤玉,等.混凝土多边形骨料分布的数值模拟方法[J].浙江大学学报(工学版),2004,38(5):61-65.

[13] ZHENG Jianjun. Mesostructure of concrete-stereological analysis

and some mechanical implications[M]. Delft: Delft University Press,2000.

[14] 郑建军,庞宪委,熊芳芳.水泥浆体初凝时间预测的数值方法及其影响因素评价[J].硅酸盐学报,2008,36(7):927-933.

[15] MOULINEC H, SUQUET P. A numerical method for computing the overall response of nonlinear composites with complex microstructure[J]. Computer methods in applied mechanics and engineering,1998,157(1/2):69-94.

[16] STOCK A F, HANNANT D J, WILLIAMS R I T. The effect of aggregate concentration upon the strength and modulus of elasticity of concrete[J]. Magazine of concrete research,1979,31(109):225-234.

[17] ZHENG Jianjun, GUO Zhanqi, HUANG Xiaofeng, et al. ITZ volume fraction in concrete with spheroidal aggregate particles and application: part II. Prediction of the chloride diffusivity of concrete[J]. Magazine of concrete research,2011,63(7):483-491.

(责任编辑：陈石平)

A numerical method for prediction of elastic modulus of concrete with polygonal aggregates

ZHOU Xinzhu1, 2, QIAN Mengbi1, ZHENG Jianjun1, 2

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2.Zhejiang Key Laboratory of Civil Engineering Structures & Disaster Prevention and Mitigation Technology, Hangzhou 310014, China)

Concrete has been widely used in construction, hydraulic, ocean, and road engineering and its elastic modulus is a key parameter for computing the deformations of structures. By combining the numerical simulation technique of the mesostructure of concrete with the fast Fourier transform, a numerical method is presented for predicting the elastic modulus of concrete. With the periodic boundary conditions, a random distribution simulation method is proposed for polygonal aggregates and interfacial transition zones (ITZs) in a cement paste matrix. The fast Fourier transform is used to give the average stress, average strain, and elastic modulus of three-phase concrete subjected to external forces. A comparison between the numerical method and the experimental data obtained from the literature is made. It is found that, when the aggregate area fraction is equal to 40% and 60%, the relative error between them is smaller than 5%, which preliminarily verifies the validity of the numerical method. Based on the numerical results, the effects of the elastic modulus and thickness of ITZ on the elastic modulus of concrete are quantified. It is found that increasing the elastic modulus of and/or decreasing the thickness of ITZ increase the elastic modulus of concrete.

concrete; elastic modulus; fast Fourier transform; polygonal aggregate; interfacial transition zone

2016-12-05

国家自然科学基金资助项目(51379188)；浙江省自然科学基金资助项目(LY15E090006)；浙江省科技计划项目(2016C33106)

周欣竹(1966—)，女，江苏南京人，教授，研究方向为混凝土材料与结构耐久性，E-mail：xzzhou66@zjut.edu.cn.

TU528.1

A

1006-4303(2017)04-0445-04