基于马尔可夫过程的路网交通状态预测方法

郭海锋，蔡华波，朱 超，查 琪

(浙江工业大学 信息工程学院，浙江 杭州 310023)

基于马尔可夫过程的路网交通状态预测方法

郭海锋，蔡华波，朱 超，查 琪

(浙江工业大学 信息工程学院，浙江 杭州 310023)

针对城市道路交通管控对路网实时交通状态信息的需求，首先对交叉口的交通状态进行了界定并划分为4个状态等级，然后以15 min为时间间隔，结合历史数据采用马尔可夫过程计算每个交叉口的状态转移概率，并对各个交叉口下一时刻的交通状态进行预测，进而对每个交叉口进行分类并采用综合评价法确定整个路网的交通状态.试验以MAPE为评价指标对已有算法进行对比，结果表明：该方法不仅能够实时地确定每个交叉口的交通状态，同时能够基于不同类型交叉口的预测结果确定整个路网的交通状态，且交叉口平均预测误差为7.04%.

城市路网；交叉口；马尔可夫过程；综合评价法；交通状态

目前，大城市交通拥堵已由偶发的个别交叉口拥堵发展为随机的局部区域性拥堵，甚至路网级的交通拥堵也已成为常态.虽然已有文献对道路交通状态评价方法的研究较为成熟[1-3]，但相关成果主要集中于对单个交叉口或路段交通状态的评估，缺乏面向区域路网交通状态的研究.董宏辉等提出[4]基于主观评价的方法确定路网交通状态的分级标准及各评价指标在线性判别模型中的权重，进而定量评判路网的交通状态等级.张和平等[5]从中观角度定义交通状态变量并建立路网交通状态模型，通过对路口交通状态分析处理，得到路口可达性、路段连通性及路网整体状态的判别结果.郭伟等[6]通过对路口检测器数据分析，利用K均值聚类和EM算法相结合，提出表征路口交通流运行状态的特征向量，并对路口状态进行分析.

文献[7-9]主要以路网可靠性、路网交通流参数均值等方式来评价路网的交通状态，且该评估方式由于考虑因素较多、限定条件苛刻以及计算相对复杂，其更适用于对路网交通状态的离线分析，而不适合指导实时的交通管控策略.为进一步满足动态交通管控的实时性要求，尤其是满足对区域性交通拥堵的优化管控需求，应采用计算快速、高效稳定的预测算法对路网的交通状态进行短时预测，并依此制定科学的交通管理和控制决策.为此，首先以每个交叉口为分析对象，然后采用马尔可夫过程对其状态进行跟踪预测，进而利用模糊综合评价法对路网整体的交通状态进行判定，最终预测路网的交通状态.

1 马尔可夫过程预测交叉口的状态

饱和状态下，路网各交叉口交通流的运行状态在前后时刻彼此影响较大[10]，因此，评估路网的交通状态不能简单地累计当前每个交叉口的交通状态，而应综合考虑当前及未来各交叉口状态的变化情况，进而对路网整体交通状态进行预测.马尔可夫过程能够较好地描述系统状态的转移情况，适用于对交叉口的状态变化进行定量描述.

1.1 马尔可夫过程

若系统t时刻及t之前时刻状态已知，t+1时刻的状态只与t时刻的状态有关，与t之前的状态无关，那么该随机过程称为马尔可夫过程.

马尔可夫过程实际上是一个将系统状态和状态转移定量化的数学模型，能够根据已知系统状态对下一时刻系统的状态进行分析和预测.确定状态转移概率是关键环节，它实际上是一个条件概率，即

pij=p(xn=j|xm=i)

(1)

式中pij表示系统在m时刻状态为i，在n时刻状态为j的可能性大小.

1.2 交叉口状态界定

交叉口是城市路网的节点，其繁忙程度直接反映了所辖范围内的交通流运行情况.在已有评价交叉口状态的指标中，服务水平和饱和度最能直观地反映交叉口的运行状态.尤其是服务水平，其能够客观地评估一个交叉口当前的运行情况，但是服务水平的获得通常采取线下分析的方式来进行，难以在线获得.然而，饱和度则可依据检测器获得的交通流量数据以及信号控制参数信息实时地获得.因此，为便于定性定量地界定交叉口的交通状态，已有相关研究成果对服务水平LOS与饱和度s之间的相关关系[11]进行了研究，描述如下(暂不考虑饱和度溢出)：0≤s<0.3，LOS=A；0.3≤s<0.6，LOS=B；0.6≤s<0.7，LOS=C；0.7≤s<0.8，LOS=D；0.8≤s<0.9，LOS=E；0.9≤s≤1，LOS=F.

考虑现实中的交通管控需求，可对上述映射关系进一步作调整[12]：LOS=A，畅通状态；LOS=B，轻微拥挤状态；LOS=，拥挤状态；LOS=F，严重拥挤状态.

1.3 交叉口状态预测

交通状态预测，是基于检测器获得的交通流量数据及历史状态数据对其下一时刻的状态进行预测分析.对于城市路网而言，在同一时间尺度上交通流变化通常呈现出较强的自相似性[13-15].因此，可通过分析历史数据获得交叉口在不同工作日各时段的交通状态信息，进而结合当前时段交叉口以及历史数据中该时段交叉口的交通状态信息来评估下一时刻该交叉口的交通状态变化情况.

为便于量化计算，将前述界定的交叉口畅通、轻微拥挤、拥挤和严重拥挤4个状态分别映射为对应等级1,2,3,4.同时，以15 min为间隔对获取的历史交通流量数据进行分析，然后计算每15 min交叉口的状态等级，进而计算交叉口状态转移概率.

交叉口在下一时刻的状态可由当前状态转换为其他几种状态中的某一种.假设交叉口当前状态为1，下一时刻状态也为1，则其状态转移概率为

(2)

式中：p11指当前状态为1，下一时刻状态为1的概率；n11指历史数据中当前状态为1，下一时刻状态为1的个数；n1指历史数据中当前状态为1的个数.

由式(2)类推，可获得不同状态间的转移概率，进而可得出交叉口下一时刻的状态转移概率矩阵为

(3)

(4)

式中pi(i=1，2，3，4)分别为交叉口下一时刻各状态概率，较大值为下一时刻的预测状态.

2 综合评价法分析路网的交通状态

路网交通状态是各个交叉口状态的综合反映，可通过各交叉口状态的变化呈现路网总的交通发展态势.通过马尔可夫过程预测出每个交叉口下一时刻的状态之后，如何以此计算整个路网的交通状态尚需进一步研究.笔者采用综合评价法并依据马尔可夫过程计算的各交叉口下一时刻的状态对路网的交通状态进行评估.

首先，将路网中的交叉口分为六类.将主干路与主干路相交的交叉口作为第一类交叉口；主干路与次干路相交的交叉口作为第二类交叉口；主干路与支路相交的交叉口作为第三类交叉口；次干路与次干路相交的交叉口作为第四类交叉口；次干路与支路相交的交叉口作为第五类交叉口；支路与支路相交的交叉口作为第六类交叉口.设路网中六类交叉口的数目分别为b1，b2，b3，b4，b5，b6，其对应的权重集合为

(5)

式中Bi=bi/(b1+b2+b3+b4+b5+b6),i=1,2,…,6.

其次，结合马尔可夫预测的交叉口下一时刻状态信息以及历史数据中交叉口下一时刻状态信息对每类交叉口进行分析.假设马尔可夫预测的交叉口畅通、轻微拥挤、拥挤和严重拥挤的数目分别为x1，x2，x3，x4；历史数据中下一时刻交叉口畅通、轻微拥挤、拥挤和严重拥挤的数目分别为y1，y2，y3，y4.便可进一步求得每类交叉口下一时刻对应状态的概率为

(6)

式中：mqi为第q(q=1，2，…，6)类交叉口的状态为i(i=1，2，3，4)的概率；u为调整参数(由经验获得，u=0.7).

获得以上数据后，可获得路网交通状态下一时刻的综合评价矩阵，即

(7)

运行状态评价矩阵可以对路网交通状态进行评定，设路网运行状态矩阵为A，其表达式为

(8)

其中

(9)

比较矩阵A中的各元素，较大值则为路网下一时刻的交通状态.

3 实验分析

3.1 数据准备

为验证提出方法的有效性，采用一个由7条主干路、3条次干路、5条支路以及32个交叉口组成的路网，其中第1类至第6类交叉口数量分别为10，8，7，2，4，1个，如图1所示，图1中数字代表交叉口类型.依据交通流的自相似性[15]等特性，采用数值模拟的方式获取了各交叉口两周内的交通流量数据，以15 min为时间间隔，分析的时间段分别为7:30—7:45；7:45—8:00；11:30—11:45；11:45—12:00.实验中主要的运算工作基于DEV-CPP的C语言开发环境完成.

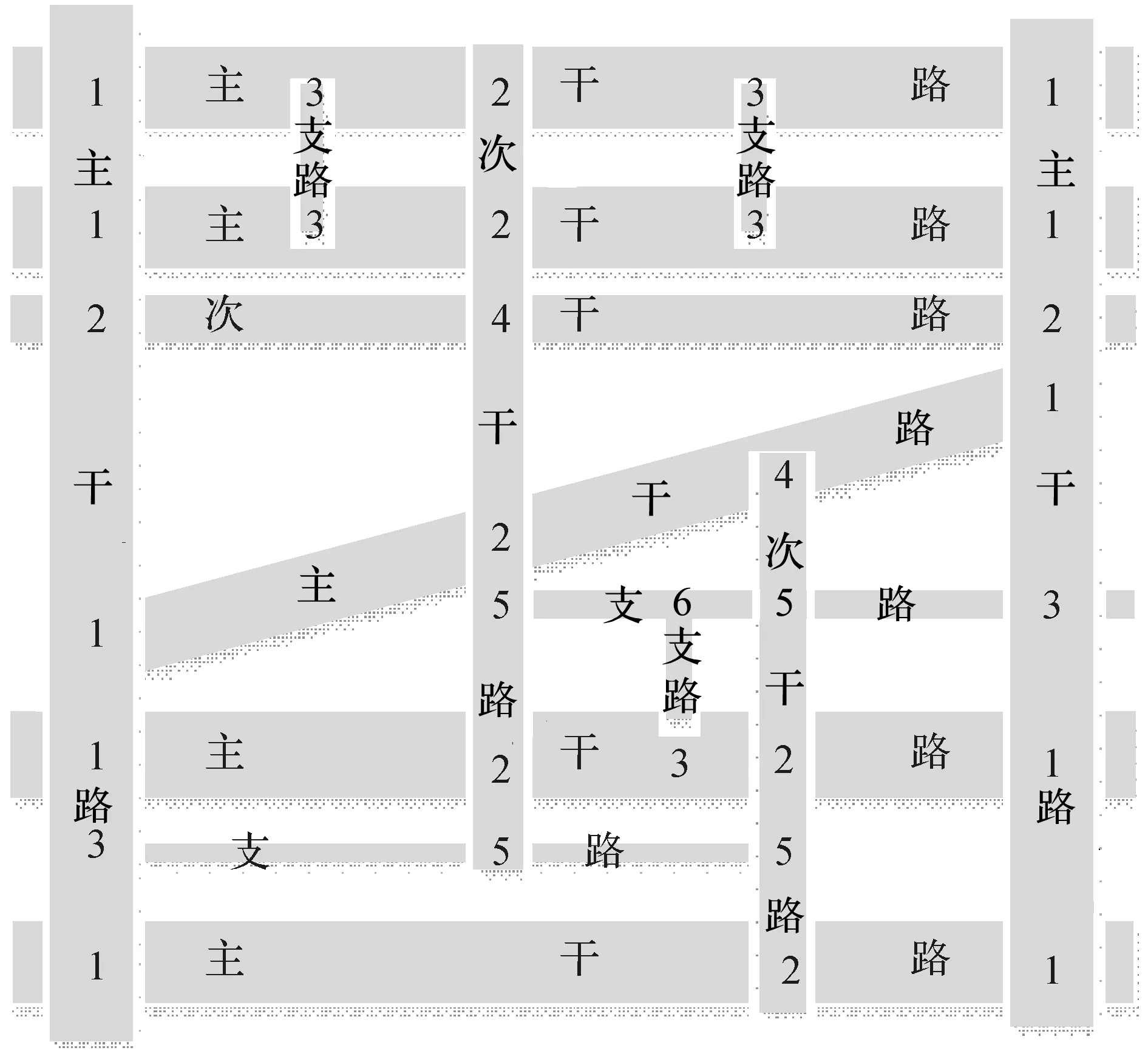
图1 简单路网图Fig.1 A simple road network

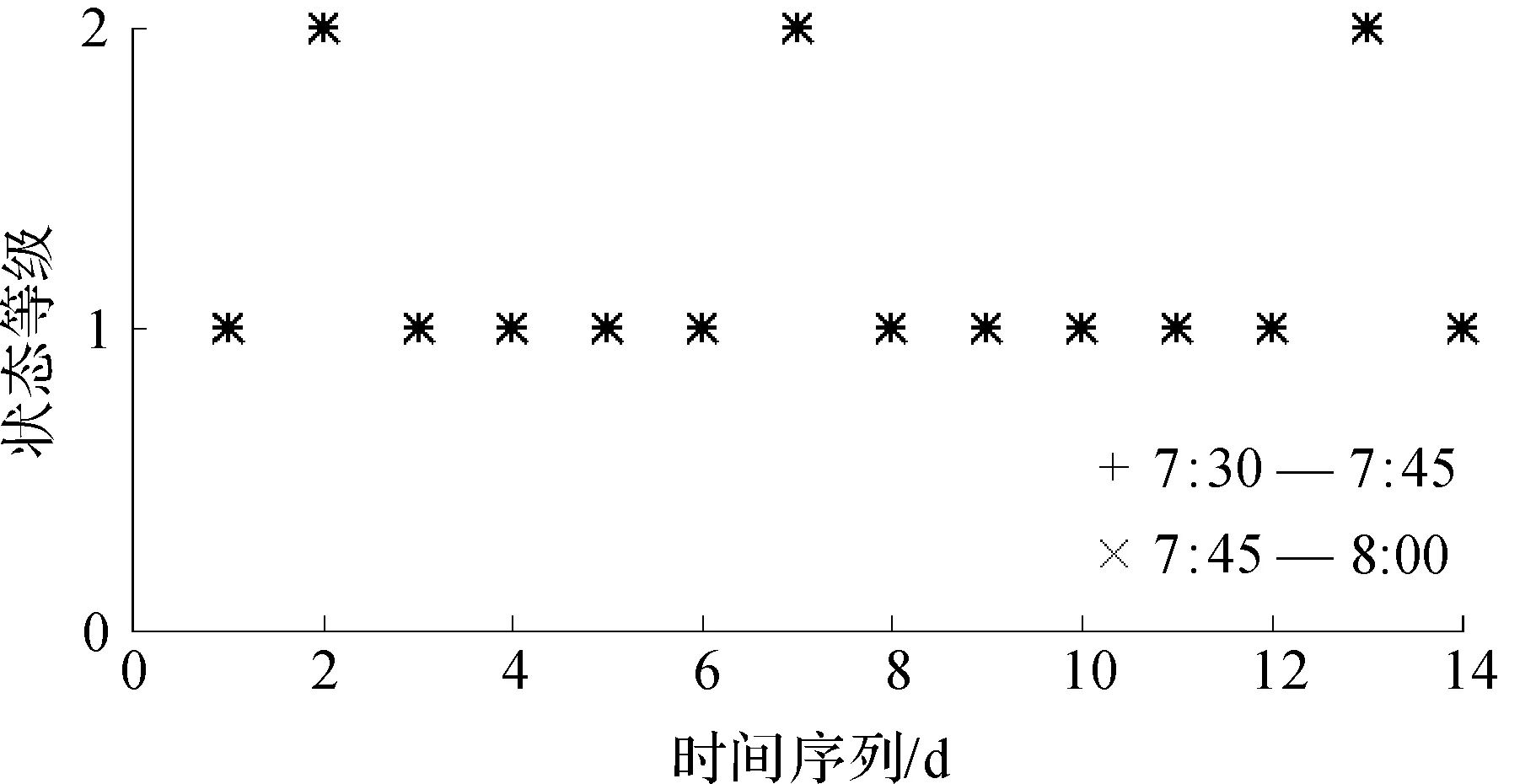
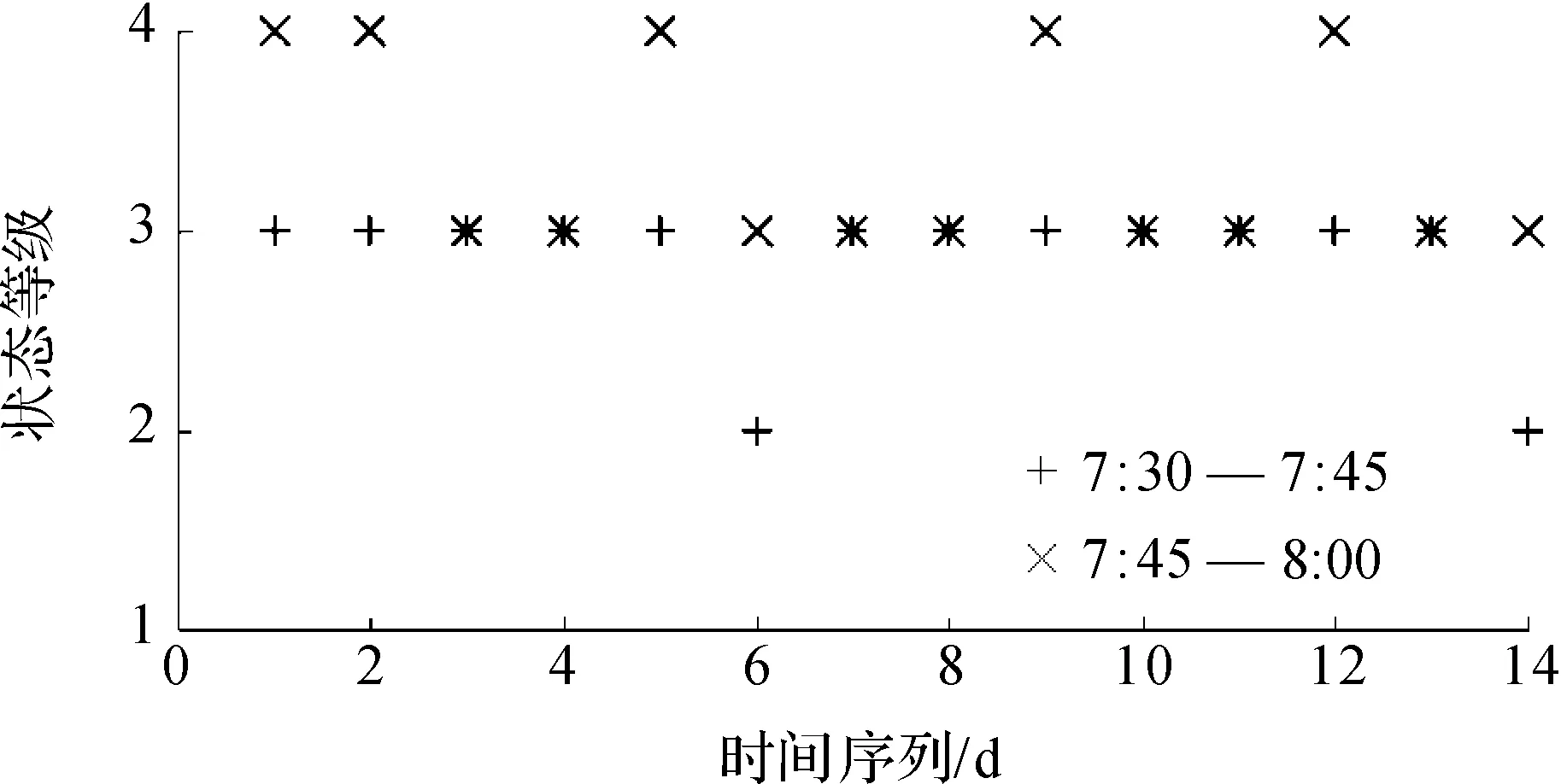
依据获取的历史数据能够获得每个交叉口各时段的状态等级，图2展示其中两个交叉口的历史数据.

为评价所提预测方法的适用性和准确性，实验中分别采用了早上和中午2组数据样本.采集当前7:30—7:45及11:30—11:45的流量计算交叉口的交通状态，然后采用马尔可夫过程对7:45—8:00及11:45—12:00的各交叉口状态进行预测.时间段分组信息如表1所示.

组别观察时间段预测时间段17:30—7:457:45—8:00211:30—11:4511:45—12:00

3.2 预测交叉口状态

图3记录了32个交叉口在组1预测时间段的预测状态及其实际状态.

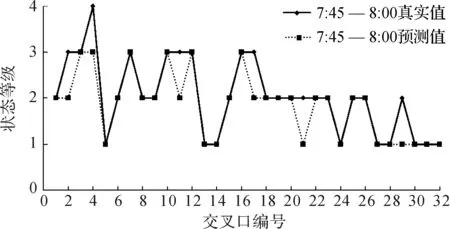
图3 交叉口预测状态及实际状态Fig.3 Predicted state and real state of intersections

采用同样的方法，对32个交叉口在组2的预测时间段状态进行预测，其预测状态及实际状态如图

4所示.

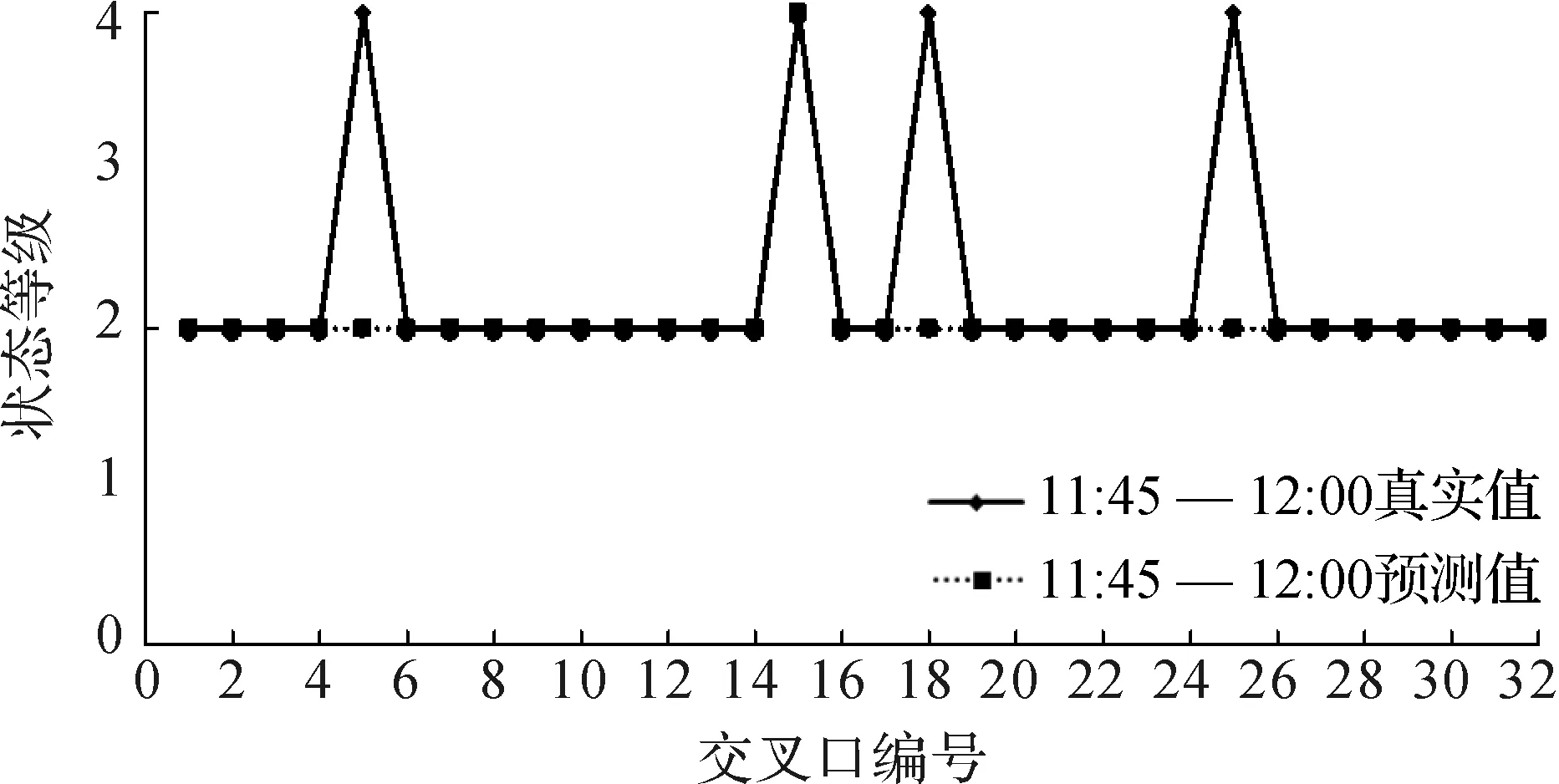
图4 交叉口预测状态及实际状态Fig.4 Predicted state and real state of intersections

3.3 确定模糊状态评价矩阵

结合预测数据及历史数据，可得出两组实验中预测时间段的路网模糊状态评价矩阵，分别为

(10)

(11)

3.4 确定路网整体状态

根据各类交叉口的权重系数，得到组1预测时间段的路网运行状态矩阵为

(12)

比较其中的四个元素，轻微拥挤状态对应的概率最大为0.53，从而得到此时路网整体状态为轻微拥挤.同理，得到组2预测时间段的路网运行状态矩阵为

(13)

再次比较，畅通状态对应的概率最大为0.94，从而得到此时路网整体状态为畅通.

图5分别给出了7:45—8:00,11:45—12:00两个时间段路网中各交叉口的预测状态，并将路网状态形象描述，前一个时间段路网呈现出的整体状态为轻微拥挤，后一个时间段路网呈现出的整体状态为畅通.

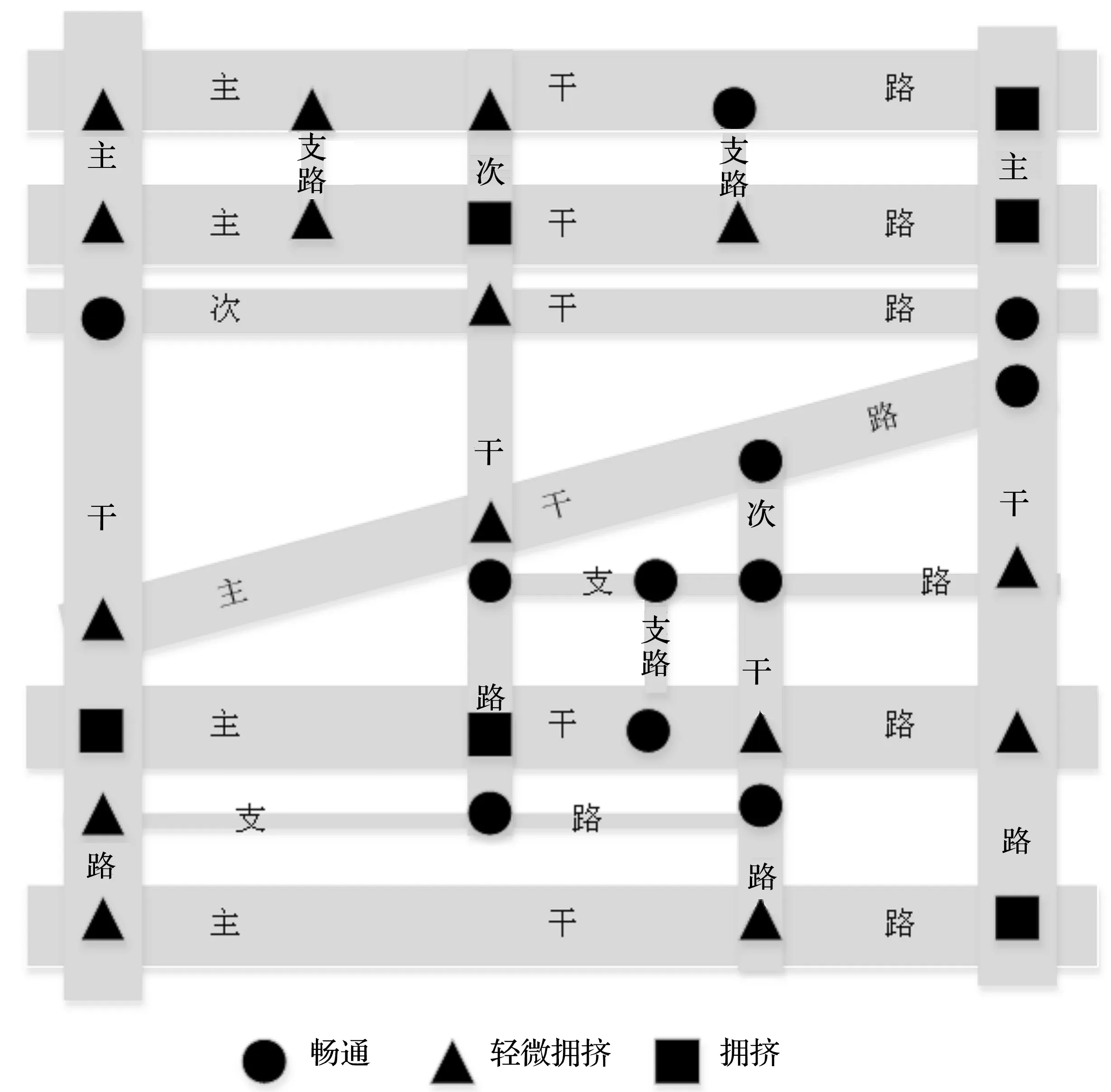
(a)预测的路网运行状态(7：45—8：00)

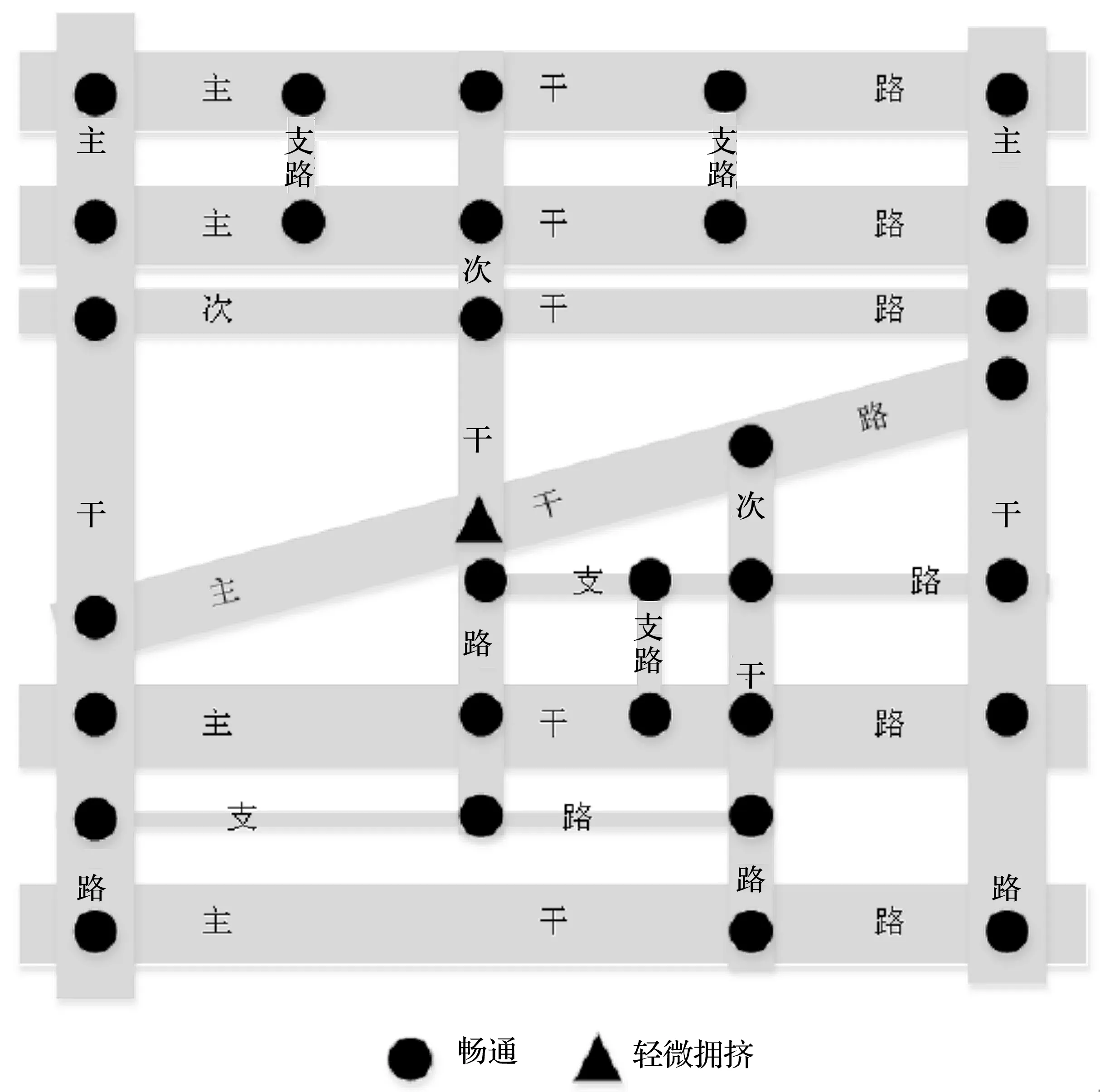
(b)预测的路网运行状态(11：45—12：00)

为说明路网交通状态预测的准确性，采用MAPE指标来评价预测精度，其采用百分比误差，表示为误差的相对量而非绝对值，从而避免了度量值大小对结果的影响.其计算式为

(14)

根据式(14)计算可得：时间段组1和组2的MAPE值分别为9.38 %，4.69 %.为便于比较，计算实验结果的平均预测误差为7.04%，如表2所示.通过对多种交通状态预测方法[16-18]进行比较分析可知：基于模糊马尔可夫过程的路网交通状态预测方法具有较好的预测精度.由于实现简单，本预测方法在多种算法中具有一定竞争力，能够很好地反映交叉口的实际状态.

表2 不同交通状态预测方法比较

表2中：ES代表指数平滑法；AR代表自回归模型；MA代表移动平均模型；ROC代表能力区域法[17]；CP代表融合预测法[16]；FMP代表模糊马尔可夫过程法.

3.5 时间性能分析

所述预测方法在实施过程中主要包括两个阶段：1) 历史数据的载入；2) 数据的处理与计算.在编程实现该预测方法时，分别在两个阶段前后加入时间获取函数便可以计算得到各阶段耗时.将程序

运行多次，得到如表3所示的结果，其中tload为数据载入耗时；tcore为数据处理与计算耗时；ttotal为两个阶段的总耗时.

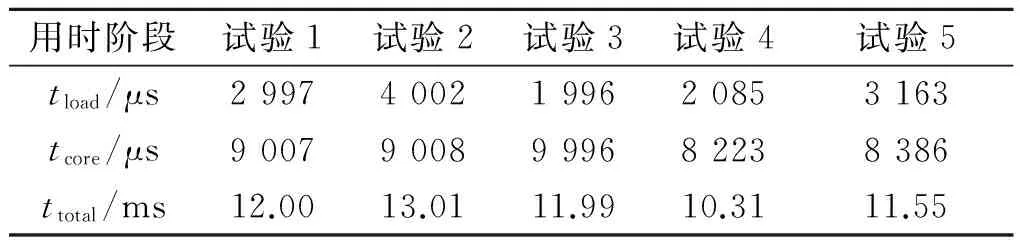
表3 方法各阶段耗费时间

分析表3可知：历史数据的载入耗时在2～4 ms范围波动，数据的计算处理在8～10 ms范围波动.尽管计算处理阶段耗时明显多于数据载入阶段(这是由于算法中含有大量矩阵计算)，但是两个阶段总耗时仍然可以稳定在10～12 ms之间.结果表明：所述预测方法对路网交通状态预测具有简单、快速的特点，且该方法实施过程耗时小、计算过程稳定，具有一定的实时性，因此适合于交通状态的预测及实时在线更新.

4 结 论

城市交通拥堵正逐步从单一路段或交叉口拥挤演化为区域性的网络拥堵，因此分析并预测路网的交通状态对未来交通管控而言越来越重要.采用马尔可夫过程对每个交叉口的交通状态进行预测，然后利用模糊综合评价法分析路网的交通状态，从而既能给出每个节点的交通状态变化情况，又能够给出整个路网的交通变化趋势.尤其是，给出的路网交通状态预测方法计算简单，适合于在线实时地预测交通状态.

本文得到浙江工业大学社科基金项目(Z20140176)的资助.

[1] 姚智胜,邵春福.基于状态空间模型的道路交通状态多点时间序列预测[J].中国公路学报,2007,20(4):113-117.

[2] 姜桂艳.道路交通状态判别技术与应用[M].北京:人民交通出版社,2004.

[3] SUN C, WANG B, ZHANG Y, et al. Urban network traffic state evaluation based on a traffic state coefficient[J]. Journal of highway & transportation research & development,2012,6(2):77-85.

[4] 董宏辉,贾利民,孙晓亮,等.城市道路宏观路网交通状态评价方法的研究[J].物流技术,2010,29(8):38-40.

[5] 张和生,张毅,胡东成,等.区域交通状态分析的时空分层模型[J].清华大学学报(自然科学版),2007,47(1):157-160.

[6] 郭伟,姚丹亚,付毅,等.区域交通流特征提取与交通状态评估方法研究[J].公路交通科技,2005,22(7):101-104.

[7] 鲁华伟,纪相财,黄利昆,等.基于马尔科夫链的道路交通状况的分析预测[J].科教导刊,2011(21):134-135.

[8] SOWUNMI F A. A markov chain approach to the dynamics of vehicular traffic characteristics in abeokuta metropolis[J]. Research journal of applied sciences engineering & technology,2009,1(3):160-166.

[9] JOHNSON E L, SIVALINGAM K M, MISHRA M. Scheduling in optical wdm networks using hidden markov chain based traffic prediction[J]. Photonic network communication,2001,3(3):269-283.

[10] 沈国江,陈文峰.方案选择式区域协调控制方法及应用[J].浙江工业大学学报,2016,44(3):237-241.

[11] 丁柏群,宋小艳.平面交叉口交通拥挤技术评价指标体系探讨[J].交通标准化,2009(2):10-13.

[12] 孙超,王波,张云龙,等.基于一种交通状态系数的城市路网交通状态评价研究[J].公路交通科技,2011,28(5):113-120.

[13] 李瑞敏,唐瑾.城市道路交通流离散模型优化分析[J].公路工程,2015,40(4):19-23.

[14] 郭海锋,方良君,俞立.基于模糊卡尔曼滤波的短时交通流量预测方法[J].浙江工业大学学报,2013,41(2):218-221.

[15] 谭满春,李英俊,关占荣,等.周相似特性下交通流组合预测方法研究[J].计算机工程与应用,2007,43(33):193-195.

[16] 聂佩林,龚峻峰.一种路网交通流参数的融合预测方法[J].交通运输系统工程与信息,2015,15(6):39-45.

[17] 刘擎超,陆建,陈淑燕.基于能力区域的交通状态预测方法[J].物理学报,2014,63(14):94-101.

[18] 孟利民,徐杨.基于动态指数平滑预测的负载均衡算法[J].浙江工业大学学报,2016,44(4):379-382.

(责任编辑：陈石平)

Prediction method of road network traffic state based on Markov process

GUO Haifeng, CAI Huabo, ZHU Chao, ZHA Qi

(College of Information and Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Aiming at demands of urban traffic control and management for real-time traffic status of road network, this paper firstly gives the definition of traffic state of an intersection and divides the states into 4 levels. Then the state transition probability of each intersection is computed by using Markov process combined with historic data at time intervals of 15 mins, and the next state of each intersection is predicted. Finally, each intersection is classified and a comprehensive evaluation method is used to predict the whole traffic states of a road network. Experimental results show that this method can not only compute the real-time traffic states of each intersection, but also can give the traffic states of the whole road network based on prediction results of different types of intersections, and the average forecast error at the intersection is 7.04%.

urban road network; intersection; Markov process; comprehensive evaluation method; traffic states

2016-12-12

浙江省自然科学基金资助项目(LY14F030012)；中国博士后基金资助项目(2012M511387)

郭海锋(1977—)，男，吉林松原人，副教授，博士，研究方向为智能交通系统，E-mail:guohf@zjut.edu.cn.

U491.14

A

1006-4303(2017)04-0421-06