结合代表点和密度峰的增量动态聚类算法

郑河荣，陈 恳，潘 翔

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

结合代表点和密度峰的增量动态聚类算法

郑河荣，陈 恳，潘 翔

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

为了解决增量大数据聚类速度缓慢问题，提出了一种结合密度峰和代表点分析的快速聚类算法.先对样本集进行初始化聚类，然后根据删除失效的聚类数据调节聚类簇群的密度均值，再利用代表点的算法对样本集进行更新，最后采用密度峰算法进行重复聚类从而更新聚类核心点.通过实验分析表明：该算法可有效提高算法收敛速度.在应用方面，将这种聚类算法引用到大数据量的人脸聚类工作中，优化人脸聚类的效果.

时效性；在线聚类；代表点；密度均值

在日益信息化的社会中，聚类分析已经成为一种被广泛应用的数据处理算法.通过聚类分析，可以发现数据的统计规则，为统计决策做出参考.特别是随着大数据时代的到来，更是需要通过高效聚类进行数据分析.聚类是将数据对象按其性质特征进行分组，使得组内数据的相似度相对较大，而组内各个元素之间的相似度较小[1].

最常用的算法是层次聚类算法[2-3]和划分聚类算法[4-5].其中层次聚类就是通过对数据集按照某种方法进行层次分解，直到满足某种条件为止，按照分类原理的不同，可以分为凝聚和分裂两种算法，Guha等[6]在1998年提出了CURE算法，该算法不用单个中心或对象来代表一个聚类，而是选择数据空间中固定数目的、具有代表性的一些点共同来代表相应的类.而常见的k-means[7]算法是一种典型的划分聚类算法，是一种迭代的算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大.该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标，但是k-means算法仅适合于数值属性数据的聚类，基于这些基础算法的局限性，又提出了许多改进的聚类算法，例如Sun Y[8]提出了一种适合于分类属性数据聚类的K-modes算法.吴天虹等[9]也在DBSCAN算法的基础上，针对其聚类缺点提出了基于维度距离的混合属性密度聚类算法.而动态聚类算法是在基本聚类算法基础上发展起来的，文献[10]提出的增量式DBSCAN算法就是在DBSCAN算法的基础上提出的，针对数据仓库环境中增量式数据加载要求，此算法是将数据进行逐一操作，没有分析数据之间的关联.文献[11]提出了基于网格的增量聚类，其算法类似于增量型的DBSCAN.黄永平和邹力鹍[12]采用批量处理的基于密度的增量聚类来克服一个个处理数据的特点，但这种算法也由于计算量过大不太能用于大数据集的聚类.文献[13]依据物理学中重力理论提出一种增量式的层次聚类，即GRIN算法，使用树状图的算法优化聚类效果.Charikar等[14]基于信息检索的需求，提出基于层次凝聚的增量聚类算法，即当以增量数据提交给算法时，要么分配给已知簇，要么形成一新簇同时合并已知簇.张忠平等[15]在C均值聚类算法的基础上引入简单的干扰数据过滤，实现了对增量数据的处理.还有基于不确定性数据而提出的基于三角模糊函数的聚类算法[16]和基于数据场和单次划分的聚类算法[17].这些基于基础聚类算法的增量聚类算法都比较耗时且聚类效果也得不到保证，可扩展性差，没有起到压缩数据的作用.受於跃成等[18]基于高斯混合模型的增量式聚类算法的启发，提出一种在基于密度峰的聚类算法的基础上，对增量和失效的数据用代表点的算法进行处理，其核心在于用少量的数据来描述原有样本的结构信息，在对增量后的样本集进行再聚类时利用这些代表点信息结合新增数据点信息进行聚类，从而达到动态聚类的效果.

1 算法架构

对于大规模数据增量聚类，在数据集合发生变化时需要考虑快速完成聚类更新，在线聚类算法流程图如图1所示.算法首先采用已有数据集合进行初始化聚类.对于增量数据，为了保证更新后的数据聚类过程能够快速收敛，在这里，根据已有聚类结果对已有数据进行代表点选择，过滤掉干扰点和异常点，提高收敛速度.最后把增量数据和过滤后的数据进行合并，通过密度峰做联合聚类，得到新的聚类结果.

图1 算法的流程图Fig.1 Flow chart of algorithm

为了描述方便，在这里给出聚类算法所需的各种定义：

1) 样本集：待聚类的数据点集.

2) 截断距离dc(Cutoff distance)：判断一个数据点是否在另一个数据点周围的参数，若两个数据点的距离小于截断距离，则这两个数据点相距很近.

3) 截断距离参数t：是确定截断距离的参数，由用户事先确定，将所有点与点之间的距离进行升序排序后取第t%的距离作为截断距离且t∈(0,100)，经实验证明当t取1至3的区间内时聚类结果比较准确.

4) 聚类核心点：是在聚类后能被划分到簇群的数据点(包括聚类中心点)，其特点是局部密度相对较大，而且与比它密度大且距离最近的点之间的距离相对较近.

5) 干扰点：在聚类完成后无法被划分进簇群的点，其特点是局部密度小，而且与比它密度大且距离最近的点之间的距离相对较远.在一次聚类后干扰点会被去除，不会带入下次的聚类.

6) 失效点：指在一次聚类和下一次聚类的间歇期中由于时效过期“死亡”的数据点、出现异常的点和人为删除的点.

7) 聚类簇群：是以聚类中心点为核心、分布相对集中的数据点集，并且有明确的边界划分.由聚类核心点组成，每个数据点能且仅能被划分到一个簇群.

2 在线聚类算法细节

2.1 聚类初始化

有一个待聚类的样本集：

(1)

对于P中任意的一个数据点xi，都有它的局部密度，即

(2)

式中：dc为截断距离，很明显与xi的距离小于dc的数据点越多，局部密度也就越大；dij为数据点xi与xj之间的距离.

ρq1≥ρq2≥…≥ρqN

(3)

可将这个数据点与比其密度大且距离最近的数据点的距离表示为

(4)

可知当xi具有最大的局部密度时，δi表示P中与xi距离最大的数据点与xi之间的距离；否则δi表示在所有的局部密度大于xi的数据点中，与xi距离最小的数据点与xi之间的距离.至此，对于每个P中的数据点都存在(δi，ρi)，可以从这两个值来确定该点是否为聚类中心，但是往往实验中更多会使用决策图的算法手工划分中心点，这种手工的方式不太适用于动态聚类的实际要求，所以使用γi作为划分中心点的依据为

γi=δiρi,i∈IP

(5)

式中IP={1,2,3,…,N}为相应的指标集.将所有的γi从大到小降序，取前若干个数据点作为中心点，取的个数由实际数据决定.

(6)

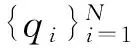
2.2 代表点选择

根据密度峰聚类算法的特性，使用代表点算法对来处理增量的数据，核心在于使用相对较少的数据点来描述原有数据点集的特点，希望利用这些代表聚类簇的代表点，并结合新增样本进行再聚类.

(7)

式中：L为该CK簇的样本总数；ρj为在这个簇群内每个数据点的局部密度.在一个簇群内有数据被删除时，对它们所在簇群的密度均值进行调节：

(8)

这样就能从簇群密度上体现这些数据点的流失，而这个密度均值会参加到后面的增量聚类中.例如，原本一个簇群在进行增量聚类时用若干个代表点来代表，而当该簇群中有失效的数据时，在下一次聚类的工作中，由于该簇群的密度均值变小，所以取到代表点的个数也相应减少.

接下来需要选取簇群的代表点，首先先确定每个簇群代表点的个数，设存在阈值nc(用户指定)，若一个簇群的核心数据点个数不超过nc，将取该簇群中所有的点作为代表点，因为这个簇群内的数据点数量原本就很小，若再选取较少的数据点来代表该簇群，就很有可能失去这个簇群的密度属性.而当簇群内数据点的个数大于nc时，簇群代表点的个数是根据簇群核心区域的面积M和簇群的密度均值m确定的，密度大且面积小的可以取相对较少的代表点，而密度小但面积大的则可以适当多取代表点，最终确定的个数在该簇群内数据点总数的40%～60%比较合适.

确定每个簇群代表点的个数后，在簇群区域内随机取点，使得取到的代表点能基本体现这个簇群的密度分布和基本形状.

2.3 密度峰聚类

采用密度峰算法[19]进行聚类核心点的更新，这种聚类算法的优势在于在已知所有数据点之间相互“距离”的情况下可以快速地查找出聚类中心点，由于其中的“距离”是欧式距离，适用的情况也比较多.在得到代表点以后，对于新增数据点，算法将原有簇群代表点结合增量数据，形成新的样本集，即

P=P代表点+P新增-P失效

(9)

(10)

式中L′为簇群加入新增数据后数据点的个数.这样无论要处理新增数据还是失效数据都可以动态调节每个簇群的密度均值，动态取到代表点加入到以后的重复聚类.然后完成密度峰聚类如下：

1) 给定用于确定新截断距离dc的参数t∈(0,100).

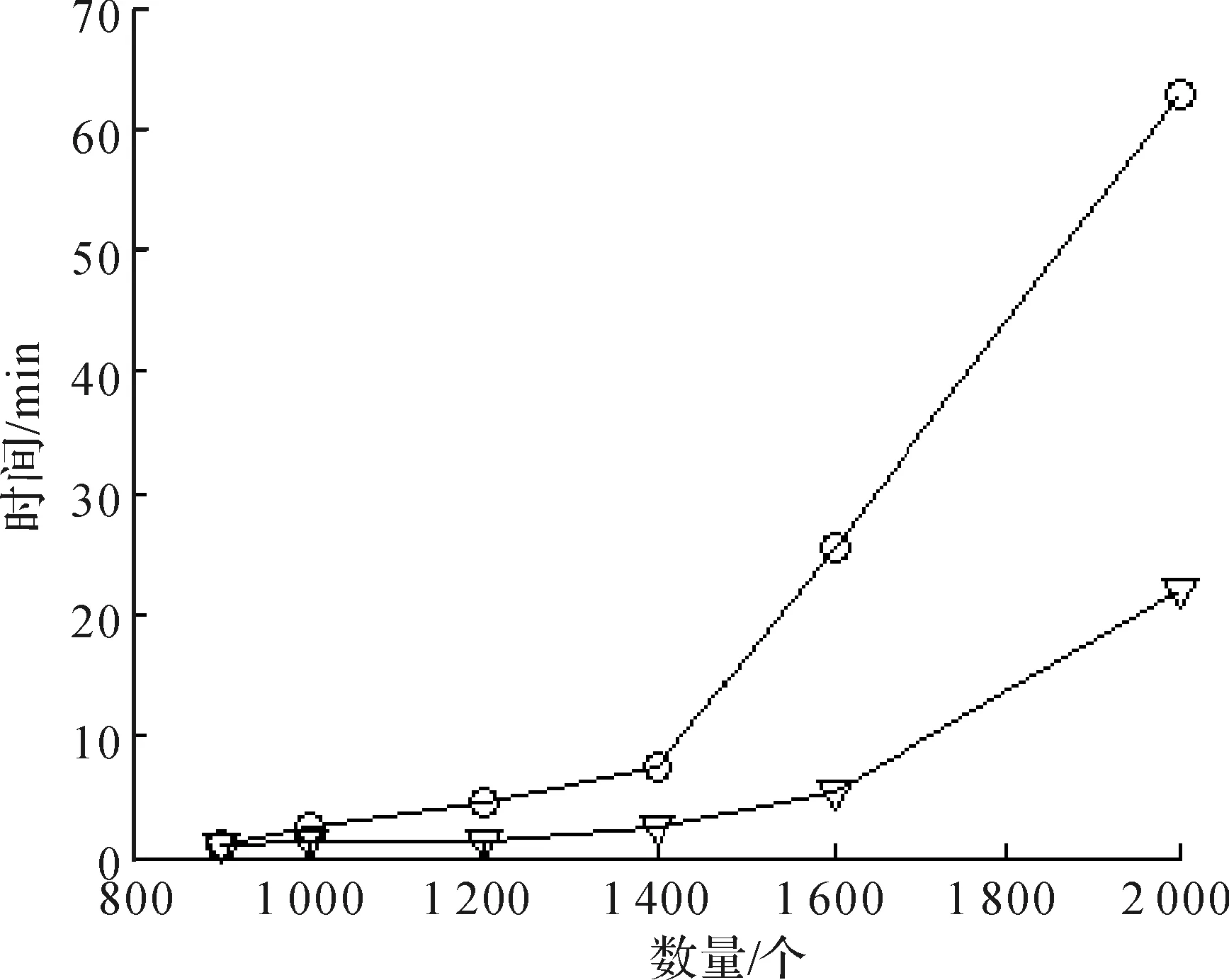
2) 计算新数据集所有的距离dij，并令dji=dij，i

(11)

7) 然后将每一个生成的簇群中的数据进一步的划分，划分为核心点和干扰点.

9) 最后在各个簇群的核心数据点中继续获取代表点，等待下一次新增数据的到来.

3 实验结果与分析

为了能够验证算法的有效性，此章节对算法和已有典型聚类算法进行实验比较分析.首先对算法的聚类效果进行可视化分析，验证代表点算法在提高算法效率的同时，能够保证聚类效果.然后对算法效率进行分析，验证在数据集增加的前提下，算法效率要明显优于已有聚类算法.最后，讨论了算法在人脸大数据中的应用.

3.1 算法聚类效果分析

首先使用以往比较常用的聚类数据集进行密度峰的聚类结果分析，例如图2(a)的分布情况，可以看到：图2(a)中中间部分的数据点相距比较紧密，其中有15个簇群，比较难划分,若使用k-means算法对该数据点集进行聚类，k的参数取到7以上时，其算法已经难以收敛，聚类效果也很差，无法将该数据点集进行良好的划分.而使用密度峰聚类算法，计算数据点集中所有点的ρ和δ值，将这些值投影到一个坐标轴上，可以看到：图2(b)中还是明显分离出了这几个γ值较大的点，选取这几个点为聚类中心点，之后将其他的数据点按局部密度大小依次划分到密度比它们大且离它们最近的点.从图2(c)中的结果可以看到：不管是外围的数据点还是中间比较密集的数据点都可以得到很好的划分.图2(d)为其他数据点集的聚类效果图.

图2 实验数据点集的聚类效果及每个点ρ值与δ值的分布Fig.2 Clustering effect of experimental data set, the ρ and δ of each point

然后使用高斯分布的数据点对dc的参数进行实验，图3(a)中使用的是t取1的参数，黑色的小点为离群点，“×”的簇群范围过大，簇群的边界不明显.图3(c)是将参数t取2，聚类的结果可以通过图3(b,d)看出：当dc距离变大，点的局部密度也增大了，而聚类核心的区域变小了，凸显出了这个簇群，效果会更好.

图3 不同dc的聚类效果图和分布图Fig.3 Clustering effect diagrams and distribution graphs for different dc

3.2 增量大数据的聚类效果分析

传统的聚类算法由于没有针对变动的数据集采取优化处理，往往导致聚类速度缓慢，特别是当有新增数据加入数据集时，之前已聚类的数据还会参加到下一次的聚类中，这严重影响了聚类效率.基本的密度峰聚类算法时间复杂度为O(n2)，是计算所有点两两之间的距离，同时计算所有点的局部密度，也需要遍历到所有点，所以当一次聚类的数据点个数不断增多时，如图4(a)中圆型的线段，所耗的时间会呈现一个指数的上涨，而三角形的线段是使用代表点的增量聚类算法，算法的速度很大程度取决于每次增加的数据点数量和每次聚类后干扰点的数量，可以看到运行的时间得到比较好的优化.图4(c)是由图4(b)使用代表点算法后的数据点分布，可以看到图4(c)中基本表达了图4(b)中簇群的形状特征和密度分布.因为密度峰的聚类算法的本质是根据各个数据点的距离关系进行聚类的，所以我们可以使用尽量少但能凸显集群中距离关系的代表点对数据集进行再聚类，从而在保证聚类效果的基础上达到时间上的优化.

之后在图3(c)的基础上选择代表点后进行再聚类，而图4(d)再聚类后的效果图，可以看到已经聚类过的簇群可以良好地进行增量再聚类，而图4中中心区域是新聚类的簇群，得到了较好的聚类效果，达到了预计的增量聚类效果.

(a) 基础密度峰聚类和代表点增量聚类时间的比较

(b) 已聚类完成的数据点集

(c) 由图4(b)得到的代表点数据点

(d) 图3(c)数据集动态改变后的聚类效果图

在实验图3(c)的基础上增加随机的数据点、减少原有的实验数据点来模拟动态聚类的情况，如图5(a)所示，随机增加了整体数据点的数量，大量减少了原来右下角“+”簇群的个数，得到ρ和δ值的分布图，如图5(b)所示.

(a) 图3(c)改变后的数据点集

(b) 对应图5(a)的ρ值与δ值的分布

可以看出在图5(a)中左侧“×”簇群和圆点簇群基本不变，只是少量增加了随机添加的数据点，而右下角“+”簇群显然减少了许多的数据点，其中心点的密度大幅减小，簇群的边界的范围也被压缩地很小，若每次聚类后其中心点的局部密度过低，则不会再将其聚类成一个簇群.动态的聚类在有数据失效后，簇群将失效的数据排除，并调整其整体密度均值，之后重复聚类时取得代表点个数也会相应减少.

3.3 在人脸聚类分析中的应用

现如今越来越多的聚类分析已经能广泛地应用在人们的生活中，根据增量聚类算法的特性，可以应用到许多生活中的数据处理.例如，现在几乎所有人通过很多的电子设备进行照相留念，久而久之会有越来越多的照片存放在手机或者是电脑上，如何对这些照片进行清理，将有人脸的照片进行分类是具有实际价值的.

实验希望通过在线的聚类算法来对人脸照片进行清洗，但在做照片聚类之前需要先对照片进行预处理；实验使用卷积神经网络的算法提取人脸特征值，卷积神经网络是近年发展起来，并引起广泛重视的一种高效识别算法.20世纪60年代，在研究猫脑皮层中用于局部敏感和方向选择的神经元时发现其独特的网络结构可以有效地降低反馈神经网络的复杂性，继而提出了卷积神经网络(Convolutional neural networks，简称CNN)，借鉴了这种算法，其优点是输入的值是图片，可以比较快速地提取特征值.从人脸照片中提取出相应的特征值后，需要计算不同特征值之间的差异程度，实验使用的是联合贝叶斯算法Joint Bayesian，至此，对照片的初始化完成.

实验使用了1 340张各类的初始人脸图片进行在线聚类，也在其中添加了一些干扰图片，包括一些不含人脸的照片.从实验结果来看：能较好较快地实现人脸聚类，将不同人的照片区分开来，而随着时间的累积，会有新的照片集进入也会有一些人工删除的照片来模拟用户日常的操作，实验结果也达到我们预期的目标.图6是取聚类后的部分实验结果.可以看出，同一个人的照片能够很好地聚类在一起，并且不受样本数目的影响.

图6 人脸聚类效果Fig.6 Face clustering effect diagram

4 结 论

提出了一种基于密度峰的动态聚类算法对大数据集进行聚类.该算法使用代表点算法和簇群的密度均值来实现对动态大数据集聚类的优化，在保证聚类准确率的同时大大提高了收敛速度，可适用增量大数据量的聚类分析.但是该算法研究只是考虑对大数据的增量聚类，并没有考虑流式数据的聚类分析.在后续工作中可以进一步提高该算法的实时性，对流数据进行实时增量聚类，提取出流数据的内在规则.另外一方面，可在聚类算法应用上做进一步研究，特别是和深度学习的特征提取相结合，可进行大数据的特征分析.

[1] JING L, NING M K, HUANG J Z. An entropy weightingk-means algorithm for subspace clustering of high-dimensional sparse data[J]. IEEE transactions on knowledge and data engineering,2007,19(8):1026-1041.

[2] WILLIAMS C. A mcmc approach to hierarchical mixture modeling[J]. Advances in neural information processing systems,2000，45(15):680-686.

[3] FRALEY C. Algorithms for model-based Gaussian hierarchical clustering[J]. Siam journal on scientific computing,1998,20(1):270-281.

[4] DING C, HE X. K-nearest-neighbor consistency in data clustering: incorporating local information into global optimization[C]//ACM Symposium on Applied Computing. New York, USA: DBLP,2004:584-589.

[5] 李洁，高新波，焦李成.一种新的特征加权模糊聚类算法[J].电子学报,2006,34(1):412-420.

[6] GUHA S, RASTOGI R, SHIM K, et al. CURE: an efficient clustering algorithm for large databases[J]. Information systems,1998,26(1):35-58.

[7] RIGELSFORD J. Pattern recognition: concepts, methods and applications[J]. Assembly automation,2002,22(4):318.

[8] SUN Y, ZHU Q M, CHEN Z X. An iterative initial-points refinement algorithm for categorical data clustering[J]. Pattern recognition letters,2002,23(7):875-884.

[9] 吴天虹，黄德才，翁挺，等.基于维度距离的混合属性密度聚类算法研究[J].浙江工业大学学报,2009,37(4):445-448.

[10] ESTER M, KRIEGEL H P, SANDER J, et al. Incremental clustering for mining in a data warehousing environment[C]//International Conference on Very Large Data Bases. San Francisco, USA: Morgan Kaufmann Publishers Inc,1998:323-333.

[11] 陈宁，陈安.基于密度的增量式网格聚类算法[J].软件学报,2002,13(1):1-7.

[12] 黄永平,邹力鹍.数据仓库中基于密度的批量增量聚类算法[J].计算机工程与应用,2004,29:206-208.

[13] CHEN C Y, HWANG S C, OYANG Y J. An incremental hierarchical data clustering algorithm based on gravity theory[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Taiwan: Springer-Verlag,2002:237-250.

[14] CHARIKAR M, CHEKURI C, FEDER T, et al. Incremental clustering and dynamic information retrieval[C]//ACM Symposium on the Theory of Computing. New York，USA: ACM,1997:626-635.

[15] 张忠平，陈丽萍.基于自适应模糊C-均值的增量式聚类算法[J].计算机工程，2009，35(6):60-65.

[16] 陆亿红，翁纯佳.基于三角模糊数的不确定性数据聚类算法[J].浙江工业大学学报，2016,44(4):405-409.

[17] 张霓，陈天天，何熊熊.基于数据场和单次划分的聚类算法[J].浙江工业大学学报，2016,44(1):52-57.

[18] 於跃成,生佳根.基于高斯混合模型的增量式聚类[J].江苏科技大学学报,2011,25(6):591-601.

[19] RODRIGUEZ A, LAIO L. Clustering by fast search and find of density peaks[J]. Science,2014,27(344):1492-1496.

(责任编辑：陈石平)

An incremental dynamic clustering method based on the representative points and the density peaks

ZHENG Herong, CHEN Ken, PAN Xiang

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

In order to solve the speed slow problem of clustering the incremental large data, this paper proposes a fast clustering method based on the representative points and the density peaks. Firstly, this algorithm uses the method of representative points to achieve clustering the incremental large data. According to deleting the invalid cluster data, the average density of cluster is adjusted. Then the algorithm of representative points is used to update the samples. Finally, the algorithm of density peaks is used to repeat clustering in order to update the core point. The experimental results show that the algorithm can effectively improve the convergence speed of the algorithm. In the application aspect, this clustering algorithm can be used in face clustering work with the large amount of data and optimize the effect of face clustering.

timeliness; online clustering; representative points; density mean value

2016-12-12

浙江省科技厅项目(2016C31G2020061)；浙江省自然科学基金资助项目(LY15F020024)

郑河荣(1971—)，男，浙江温岭人，教授，硕士生导师，主要从事计算机图形学与图像处理技术研究，E-mail：hailiang@zjut.edu.cn.

TP3

A

1006-4303(2017)04-0427-07