滑流对飞机纵向静稳定性影响的数值模拟

任晓峰, 段卓毅, 魏剑龙

(航空工业第一飞机设计研究院, 陕西 西安 710089)



滑流对飞机纵向静稳定性影响的数值模拟

任晓峰*, 段卓毅, 魏剑龙

(航空工业第一飞机设计研究院, 陕西 西安 710089)

针对某“机身+机翼+襟翼+短舱+螺旋桨+平尾”简化构型，开展低速大拉力系数工况下强螺旋桨滑流的数值模拟。模型为翼吊双发布局，动力计算时分为三个计算域，分别为两个包含螺旋桨的旋转域和一个静止域。采用商业软件ICEM CFD生成多块面搭接非结构网格，在机体表面和滑流区域对网格进行加密以便于捕捉螺旋桨滑流的发展及其与机翼、尾翼等部件之间的干扰。采用ANSYS CFX软件求解雷诺平均Navier-Stokes方程，使用多参考坐标系(MFR)方法模拟螺旋桨的旋转。基本构型有/无动力的计算结果表明螺旋桨动力及其产生的滑流对模型的纵向静稳定性影响较大，模型的纵向静稳定性在迎角较小时下降明显甚至丧失，在迎角较大时反而略有增加。一般而言，涡桨飞机平尾处的流场受气动布局、迎角、机翼及襟翼的下洗和螺旋桨滑流及其强度等因素的共同影响。对模型各部件的俯仰力矩特性及尾翼区流场细节进行详细分析可知，小迎角时飞机纵向静稳定性的下降是由于平尾受到机翼及襟翼较强的下洗作用而导致效率下降，而此时平尾没能进入滑流区，不能有效利用滑流区内高能气流来提高平尾效率。并且由于两个螺旋桨同为逆时针旋转，右侧平尾的贡献高于左侧平尾。为了验证这一结论，分别将螺旋桨向上平移0.7 m和将平尾下移0.86 m并进行数值模拟，结果表明平尾对模型纵向静稳定性的贡献均有增加。

螺旋桨；滑流；纵向静稳定性；数值模拟；旋转域；非结构面搭接网格；多参考坐标系

0 引 言

螺旋桨发动机因具有起飞拉力系数大、巡航状态经济效率高等优点，至今仍在飞行马赫数低于0.6的低速飞机上广泛使用，如国产的Y-7、Y-8和Y-12等系列飞机。涡桨飞机的一大特点是其动力系统对飞机的气动特性有较大的影响，在起飞和复飞等低速构型、大拉力系数工况下影响尤为明显。

通常可将涡桨飞机动力系统对飞机气动特性的影响分为直接影响和间接影响两个部分。直接影响是指由螺旋桨旋转产生的拉力、法向力(或径向力)等直接力的影响；间接影响则是指螺旋桨滑流流过机翼、尾翼等气动部件引起的全机气动特性变化。螺旋桨的拉力一般由生产厂家提供即可直接使用，法向力的准确获取主要依靠风洞试验。欧阳绍修等[1]对装机后螺旋桨径向力的风洞试验方法进行了研究，指出了螺旋桨径向力的产生机理，在风洞中获得了螺旋桨径向力系数随迎角的变化规律。

螺旋桨滑流指螺旋桨后方的流管，其轴向速度高于未受扰来流，同时存在旋转速度，在装机状态下还存在与发动机短舱、机翼、襟翼以及尾翼等部件的相互干扰，流动形态较为复杂。涡桨飞机气动特性的变化与螺旋桨滑流的强度密切相关，螺旋桨的拉力系数越大，滑流对飞机气动特性的影响量也越大。

目前，研究螺旋桨滑流对飞机气动特性的影响主要有两种方法——带动力试验和数值模拟。带动力试验通过对螺旋桨相似参数的模拟(一般采用Tc-λ或Tc-Qc方法)，可以较为准确地得到滑流对飞机气动特性的影响量。赵学训[2]在风洞中研究了螺旋桨滑流对飞机绕流的影响，指出滑流的影响区域只与螺旋桨的直径及其在飞机上的安装位置有关。滑流改变了影响区域内机翼表面的压力分布，在大部分影响区域内使流动加速，因而增加机翼升力。滑流也使平尾处的动压和下洗增加，且增量几乎正比于拉力系数。李征初等[3]针对某运输机巡航状态螺旋桨滑流对机翼的影响进行了带动力风洞试验，采用七孔探针测量滑流区的流动状态，研究了螺旋桨滑流的发展规律及其对机翼上表面压力分布的影响。刘毅[4]和任庆祝[5]等采用多天平测力技术得到了某四发涡桨运输机螺旋桨滑流对飞机升力失速特性及全机气动特性的影响量，该技术是目前比较先进的螺旋桨飞机风洞试验技术。国外对螺旋桨滑流的试验研究也在继续深入，Müller等[6]在低速风洞中获得了螺旋桨滑流对A-400M飞机气动特性的影响，Roosenboom等[7]采用平面粒子图像测速(PIV)技术研究了一个安装在机翼上的八叶螺旋桨后方滑流的发展。然而，常规的测力和测压试验还不能充分揭示滑流及其对飞机部件干扰的机理，想要直接指导螺旋桨飞机的设计还需要诸如立体PIV等技术在风洞试验中的发展和应用。

随着集群计算能力的提高和计算流体力学(CFD)的进步，采用数值模拟方法获得螺旋桨飞机的气动特性成为可能。左岁寒等[8]采用激励盘结合N-S方程对带有后缘襟翼的机翼的滑流流场进行模拟，得到了较好的结果，但是忽略了螺旋桨的旋转效应。任晓峰等[9]采用多参考系方法求解定常N-S方程，捕捉到了滑流的旋转、加速和侧洗等特点，获得了滑流对机翼表面压力分布的影响。许和勇[10]、程晓亮[11]、张小莉[12]、夏贞锋[13]、龚晓亮[14]、张刘[15]和杨小川[16]等采用非结构网格和结构化网格，通过求解非定常Euler或N-S方程开展螺旋桨滑流的数值模拟，对螺旋桨滑流的发展、滑流对机翼及增升装置表面压力分布的影响以及滑流区的流场细节进行了详细分析。Malard等[17]采用激励盘方法对螺旋桨飞机高速飞行时的流场进行了模拟。Stuermer[18-19]采用基于嵌套网格的非定常求解器模拟了螺旋桨的安装效应和前后对转螺旋桨系统的气动特性。Roosenboom等[20]将非定常计算结果与平面PIV试验结果进行了对比。徐家宽等[21]针对某涡桨飞机进行考虑螺旋桨滑流影响的机翼气动力优化设计，使巡航状态机翼和短舱的升阻比提高了3.3%。以上研究表明，采用数值模拟方法进行螺旋桨滑流影响分析效果较好。然而，目前的数值模拟大多局限于滑流与机翼的相互干扰，研究的滑流强度的较少，或者仅注重于计算方法、湍流模型等的研究。实际上，数值模拟结果可以显示飞机绕流的流场结构及细节，帮助设计师有针对性地改进部件气动设计，对螺旋桨飞机的气动布局有直接的指导作用。低速构型，发动机的拉力系数大，飞机在强滑流影响下的气动特性变化将更为剧烈。对滑流的利用如何做到有的放矢，数值模拟的指导作用将更为显著。本文针对某“机身+机翼+襟翼+短舱+螺旋桨+平尾”简化构型，开展数值模拟分析，摸清螺旋桨滑流对平尾气动特性的影响机理，提出飞机布局改进设计方向。

1 计算几何模型

以无动力“机身+机翼+襟翼+短舱+平尾”为基础构型，如图1(a)所示，定义为构型0(Model 0)。襟翼为全翼展分段襟翼，打开至起飞偏度；螺旋桨直径为4m，从机身后部朝前看呈逆时针方向旋转；平尾安装在机身后部，为低置平尾，其前缘距螺旋桨10.5 m，约2.5个桨盘直径距离；没有配置垂尾。选用某六叶螺旋桨进行带动力数值模拟，如图1(b)所示，定义为构型A(Model A)。在构型A的基础上，将螺旋桨安装位置上移0.7 m，得到构型B(Model B)；将平尾下移0.87 m，得到构型C(Model C)。螺旋桨的拉力系数定义为Tc=T/(qS)，q为自由流动压，S为参考面积。取0 km高度气体状态参数，计算风速为57.3 m/s，模型平均气动弦长为2.85 m，通过调整桨叶角使螺旋桨的拉力系数约为0.3。

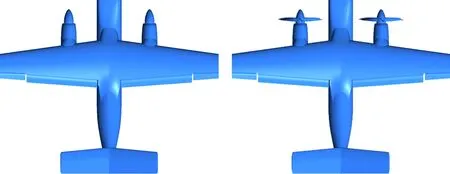
(a) 无动力 (b) 带动力图1 基础构型Fig.1 Baseline configuration

2 计算方法及算例验证

采用多块搭接非结构网格，在螺旋桨周围设置合适的圆柱形区域用以模拟螺旋桨的旋转，如图2所示，网格数量约5×107。采用商业软件ANSYS CFX求解雷诺平均Navier-Stokes方程，对流场进行数值模拟，湍流模型为Shear Stress Transport(SST)。在圆柱域内,采用多参考坐标系(MRF)方法把螺旋桨相对静止流体的旋转运动转变为旋转流体相对静止螺旋桨的运动，通过全隐式交界面进行旋转域与固定域之间的流场信息传递，保证通过交界面所有方程的所有通量都严格守恒[9]。

为了验证该方法的可靠性和准确性，针对某螺旋桨飞机进行数值模拟并与风洞试验结果进行了对比。该算例中的螺旋桨含有六个桨叶，计算状态为：马赫数Ma=0.17，雷诺数Re=1.1×107，无缩比模型，网格量约为5×107。图3给出该算例在迎角为2°时的非定常计算结果，横轴为螺旋桨相位角，纵轴为计算得到的升力系数。可见螺旋桨滑流的周期性变化导致了机翼气动力的小振幅等幅周期性震荡，震荡周期与螺旋桨转过60°的时间相同。图4为使用本文的MRF方法计算得到的升力和俯仰力矩系数结果与试验数据的对比，可见数值模拟得到的气动力系数比较准确。这些结论说明该计算方法能够为本文的滑流数值模拟提供可靠的计算基础和依据。

图2 螺旋桨和机体表面网格及旋转区域Fig.2 Surface grid of propeller and airframe and the rotating region

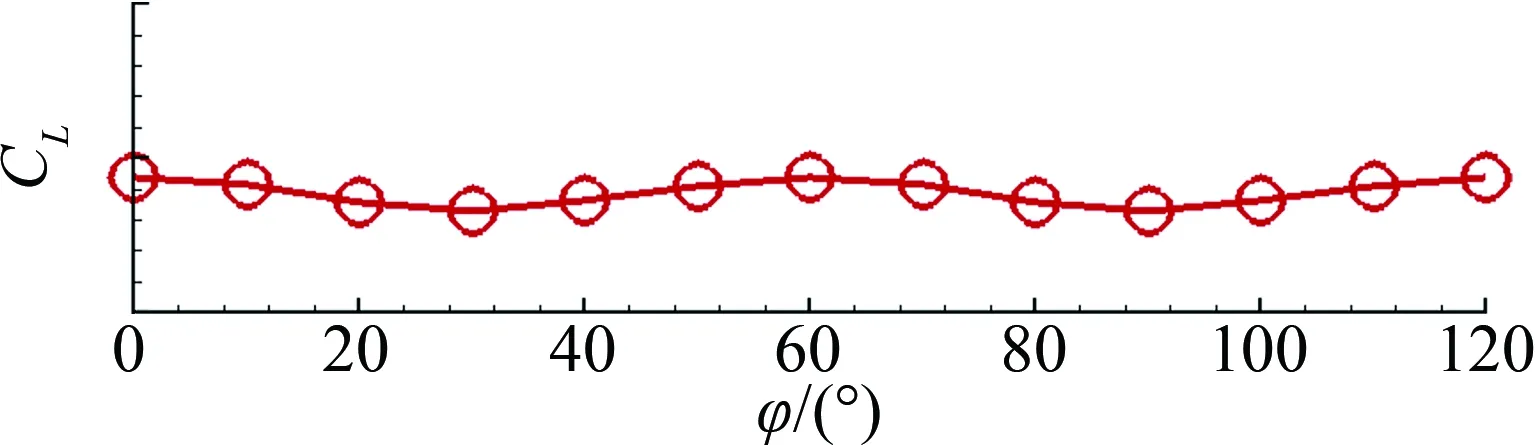
图3 升力系数非定常计算结果Fig.3 Unsteady CFD results of lift coefficient

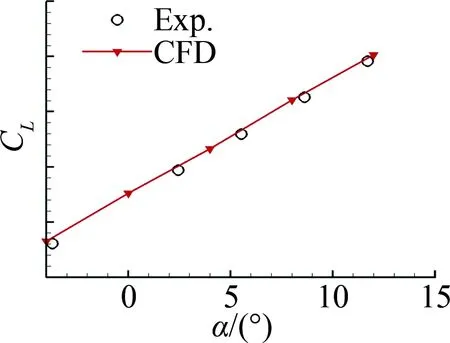
(a) 升力特性 (b) 俯仰力矩特性图4 计算结果与试验数据的对比Fig.4 Comparison of lift and pitching moment coefficients between calculation and experiment

3 模型计算结果及分析

3.1 气动力系数

图5给出计算得到的升力及俯仰力矩系数计算结果，力矩参考点选在机翼平均气动弦的1/4处。计算结果可以明显看出螺旋桨动力及滑流对气动特性的影响：

1) 模型的升力系数增大，升力线斜率增加；

2) 模型的抬头力矩增加，俯仰力矩曲线斜率减小。

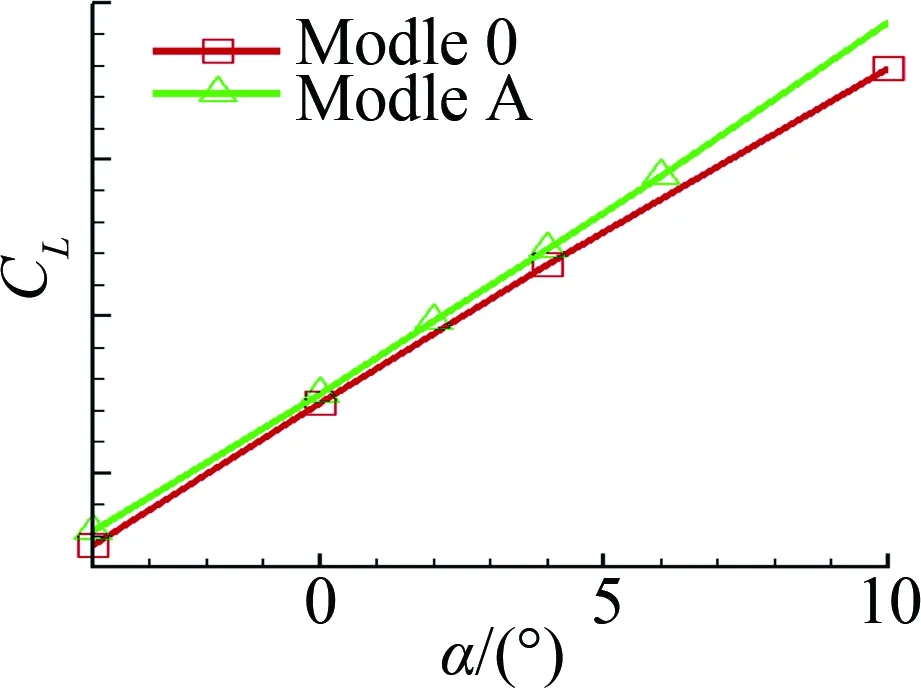
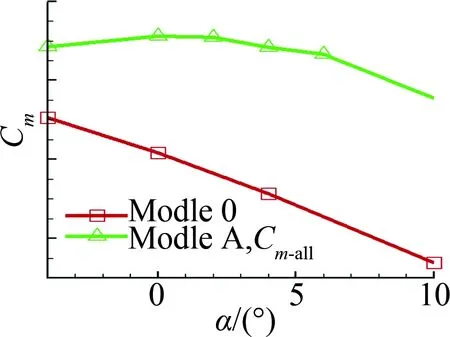
(a) 升力特性 (b) 俯仰力矩特性图5 升力及俯仰力矩系数计算结果Fig.5 CFD results of lift and pitching moment coefficients

3.2 详细分析

本文主要关心滑流对纵向静稳定性的影响，下面将针对图5(b)中的俯仰力矩曲线进行详细分析。

图5(b)表明螺旋桨动力及其产生的滑流对模型的力矩特性有较大的影响，且其影响呈现明显的非线性，在不同的迎角范围，影响存在明显的差异。在迎角较大时，两条力矩曲线的斜率基本一致，表明两个构型的纵向静稳定性裕度大致相同。而在迎角较小时，带动力构型的纵向静稳定性裕度有比较明显的下降，甚至在部分计算范围内力矩曲线的斜率为较小的正值，呈纵向静不稳定。这些现象显露出动力及滑流影响的严重性及复杂性，必须仔细分析各气动部件的气动特性变化情况及螺旋桨滑流对飞机绕流的影响，揭示螺旋桨滑流的影响机理，为涡桨飞机的气动布局及部件设计服务。

3.2.1 俯仰力矩系数计算结果

图6将构型A的俯仰力矩分解为由螺旋桨直接力引起的俯仰力矩和机体各部件产生的俯仰力矩两部分之和。可见，螺旋桨直接力使模型的纵向静稳定性下降(Cm-prop)，拉力系数为0.3时，经估算可知其减小量不小于8%。螺旋桨的拉力系数一般随迎角变化不大，如图7所示，因此可以近似认为该量即是螺旋桨法向力的影响量。扣除了螺旋桨法向力的影响之后，得到的就是带有螺旋桨滑流影响的模型俯仰力矩特性，如图6中蓝色虚线所示。可见，在大部分计算迎角下，模型的纵向静稳定裕度与无动力构型相比也有所降低。值得注意的是，在迎角比较大时，模型的纵向静稳定裕度反而要略高于无动力构型。

再将机体俯仰力矩系数分解至“机翼+机身”组合(Cm-W+B)和平尾(Cm-HT)，如图8所示。可见无动力时Cm-W+B线的斜率几乎为0，而螺旋桨滑流则使该曲线呈现出明显的拐点，在拐点之前使模型的纵向静稳定性裕度降低约10%，而在拐点之后使模型的纵向静稳定性裕度增加约8%。无动力时Cm-HT曲线线性很好，平尾提供的纵向静稳定性裕度约为24%。滑流使小迎角范围内平尾提供的纵向静稳定性裕度明显降低，减小约12%，而在计算迎角较大时，则几乎保持不变。

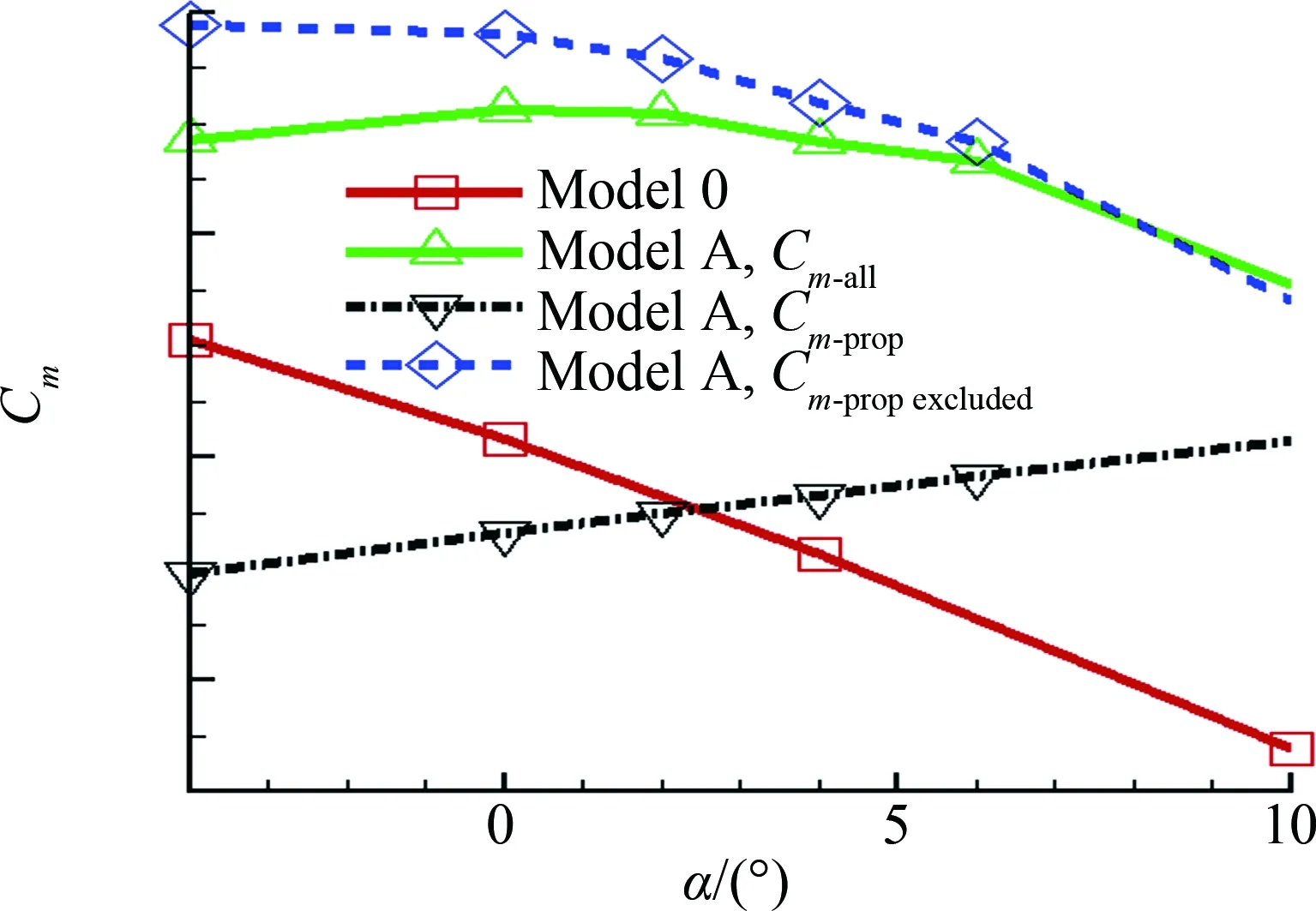
图6 构型A俯仰力矩计算结果分解Fig.6 Decomposition of pitching moment of Model A

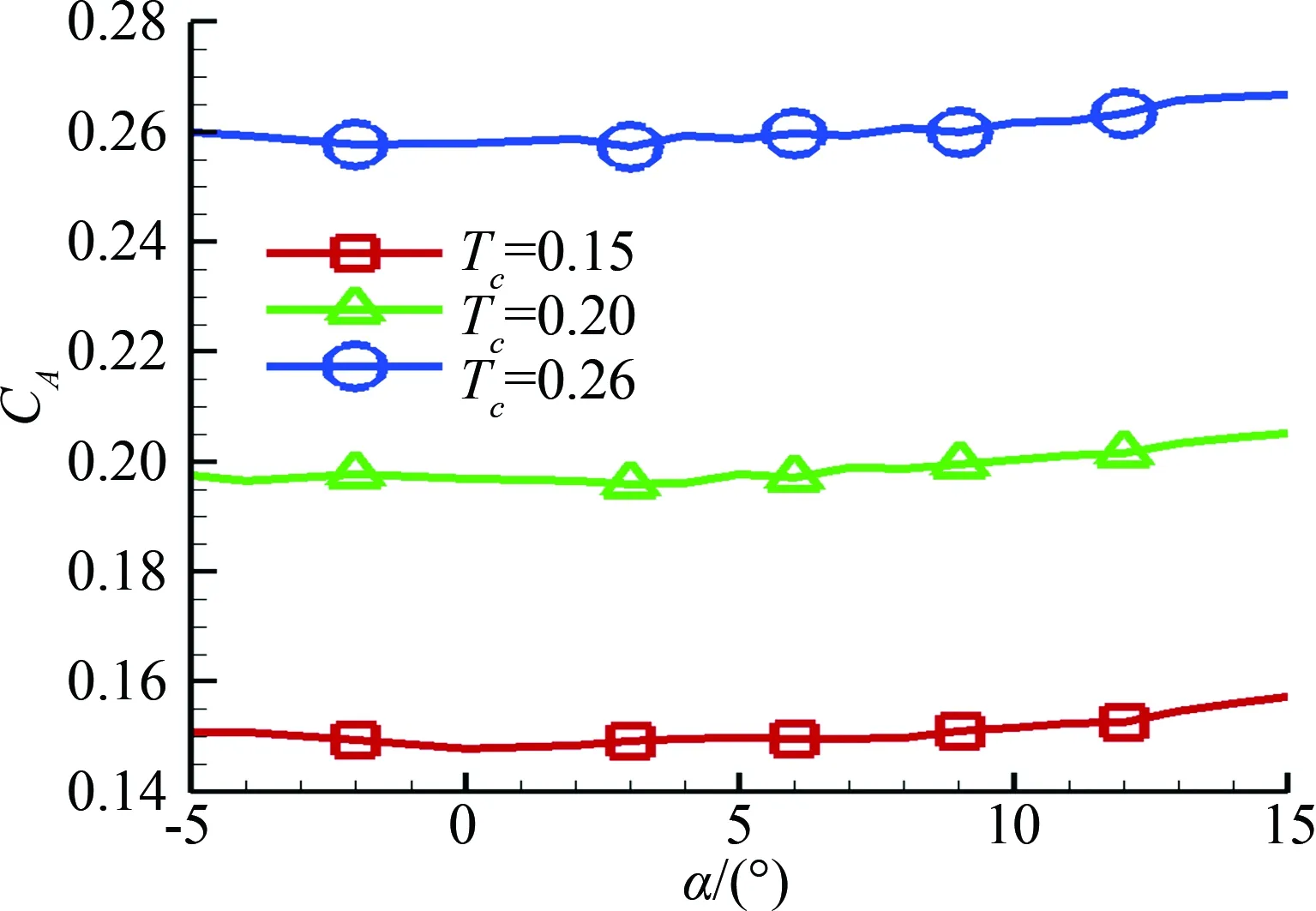
图7 螺旋桨轴向力变化趋势Fig.7 Propeller axis thrust coefficient varies with angle of attack

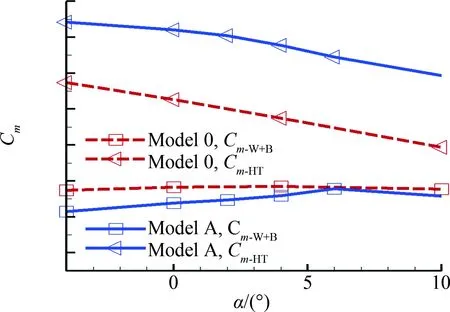
图8 机体俯仰力矩系数计算结果分解Fig.8 Decomposition of airframe pitching moment

最后将左右平尾(从机尾向机头看)的俯仰力矩系数再进行分解，如图9所示。可以看出左右两侧平尾的俯仰力矩特性在滑流影响下出现显著差别。各计算迎角下，右侧平尾产生附加抬头力矩，增量随迎角变化不大，对纵向静稳定性影响较小；左侧平尾产生的附加抬头力矩从量值上来说更为明显，但是在大部分计算迎角下对纵向静稳定性的贡献明显下降，在迎角较小时曲线斜率甚至接近于0，与平尾负迎角失速的表现有些相似，但是其背后的机理是否真的是平尾失速还需要进一步分析。

图9 平尾力矩系数计算结果分解Fig.9 Decomposition of H-tail pitching moment

3.2.2 流场细节及影响机理分析

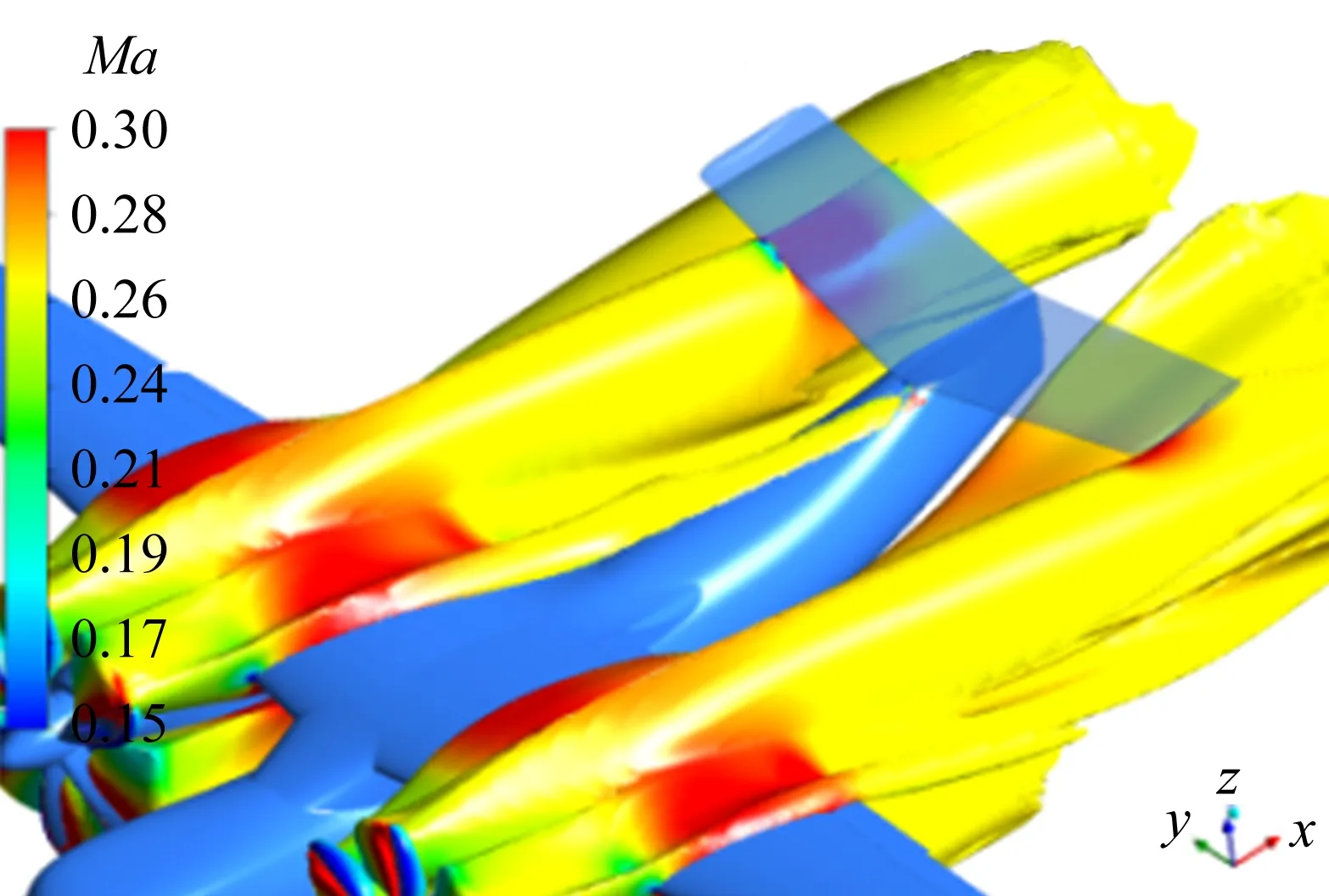
螺旋桨的动量理论指出：无穷远来流逼近螺旋桨时速度增加、压强减小；流过桨盘后压强增加、速度不变；进入滑流区压强减小、速度增大，且滑流速度增量是桨盘处速度增量的2倍[22]。赵学训[2]指出，如果平尾完全浸没在滑流区，平尾处的平均动压与螺旋桨的拉力系数线性相关，见图10，其理论值为Δq/q∞=Tc。由于滑流展向分布的不均匀性,以及螺旋桨滑流与机体的摩擦和与气流的掺混损失，加之平尾并无可能完全浸泡在滑流区，实际数值总是要明显低于理论值。本文的计算风速约为57.3 m/s，对应的动压为2011 Pa，在计算结果中均扣除了参考压力(1 atm，101325 Pa)。图11给出迎角为-4°时计算得到的螺旋桨中间剖面的速度分布。图11中可清楚看出气流在接近螺旋桨时的加速以及在桨盘后方由于短舱、机翼的存在而持续加速。在滑流发展的过程中，由于襟翼偏转及机翼升力带来的下洗也很明显。滑流的影响区域较大，直到平尾后约1个桨盘直径处，最大气流速度仍接近90 m/s。图12给出图11中滑流区内一条曲线上的速度分布，可以清楚地看到桨盘前后的气流速度变化以及平尾附近流动速度与自由流之间的差别。

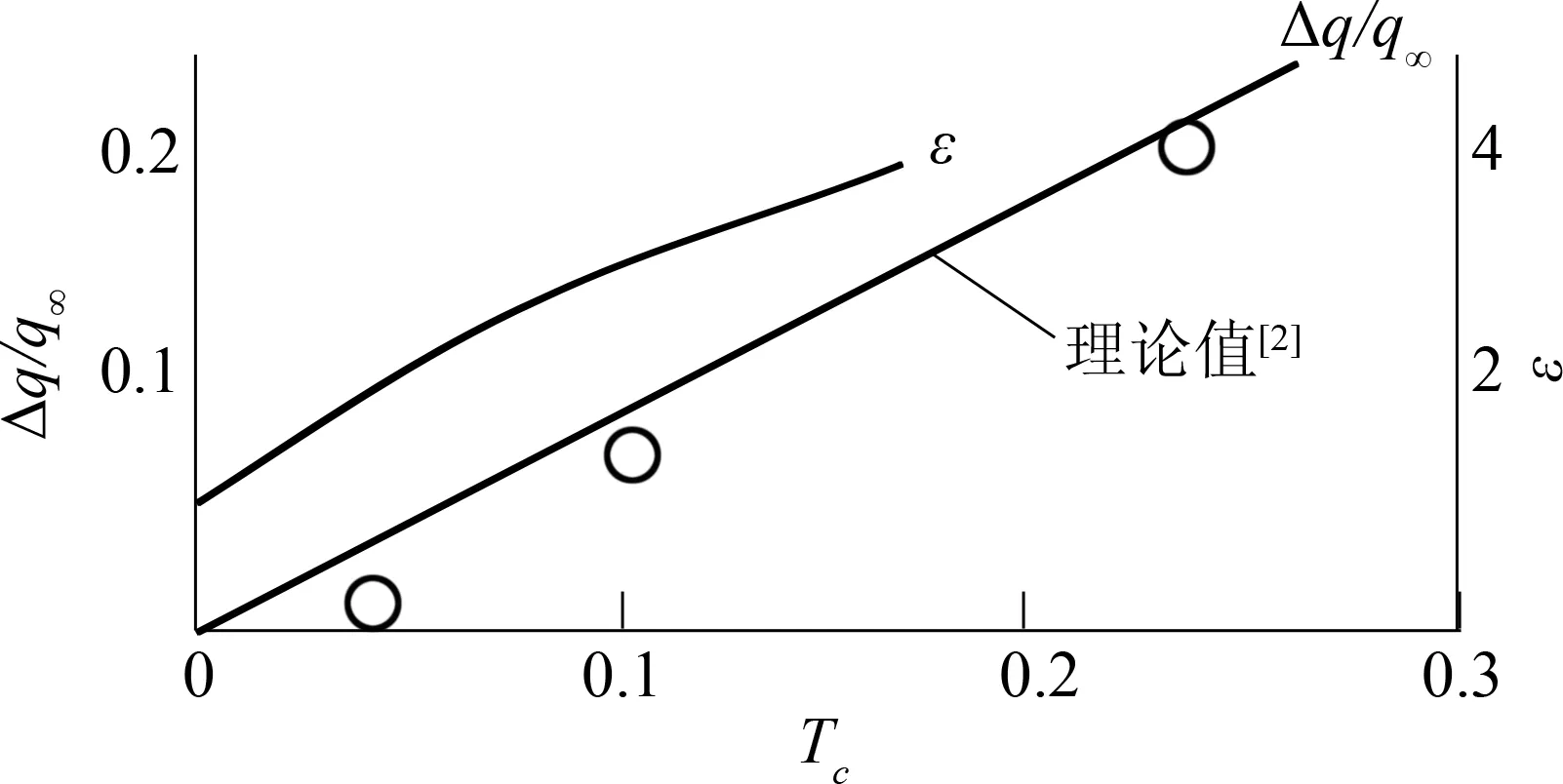
图10 平尾流动的变化(α=6°)[2]Fig.10 Flow condition of H-tail (α=6°)[2]

然而，由于螺旋桨滑流的不均匀性，对一个或几个剖面的局部分析往往不能说明问题，有时甚至可能仅仅是假象而将人带入误区。要研究螺旋桨滑流对飞机气动特性的影响，首先应对整个飞机的流场有个完整的认识。理论上，螺旋桨滑流使机翼当地升力系数提高，使机翼的升力线斜率增加，机翼后方的下洗率增加，这会减小尾翼对飞机纵向稳定性的贡献。为了减轻尾翼处受到的下洗影响，有些涡桨飞机通过采用高置平尾(T型尾翼)使尾翼远离强下洗区，如ATR72和MA700等飞机。然而，如果平尾能部分或全部浸没在螺旋桨滑流中，会由于承受的动压增加，增大平尾的有效升力线斜率，加强其对稳定性的贡献。安-24(Y-7)飞机就采用了低平尾布局，并且采用了比较大的上反角，以使平尾在飞行时不受机翼的扰动气流影响，并且使其处于螺旋桨的良好的滑流当中[23]。需要注意的是，平尾是否真正浸没于滑流区，取决于飞机迎角、襟翼偏度和发动机功率等多个参数[24]。

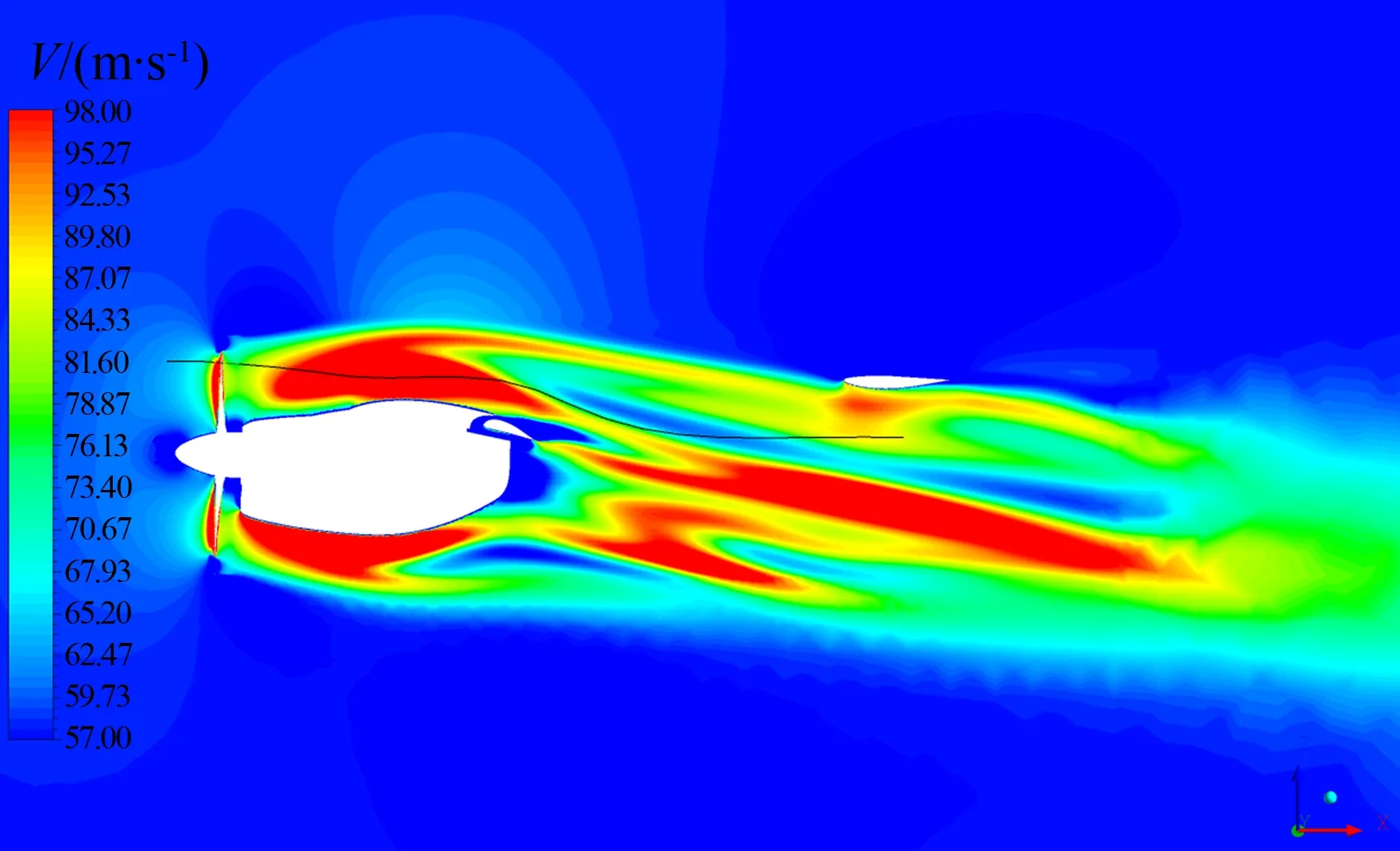
图11 螺旋桨中间剖面速度云图Fig.11 Velocity contour of the propeller symmetric plane

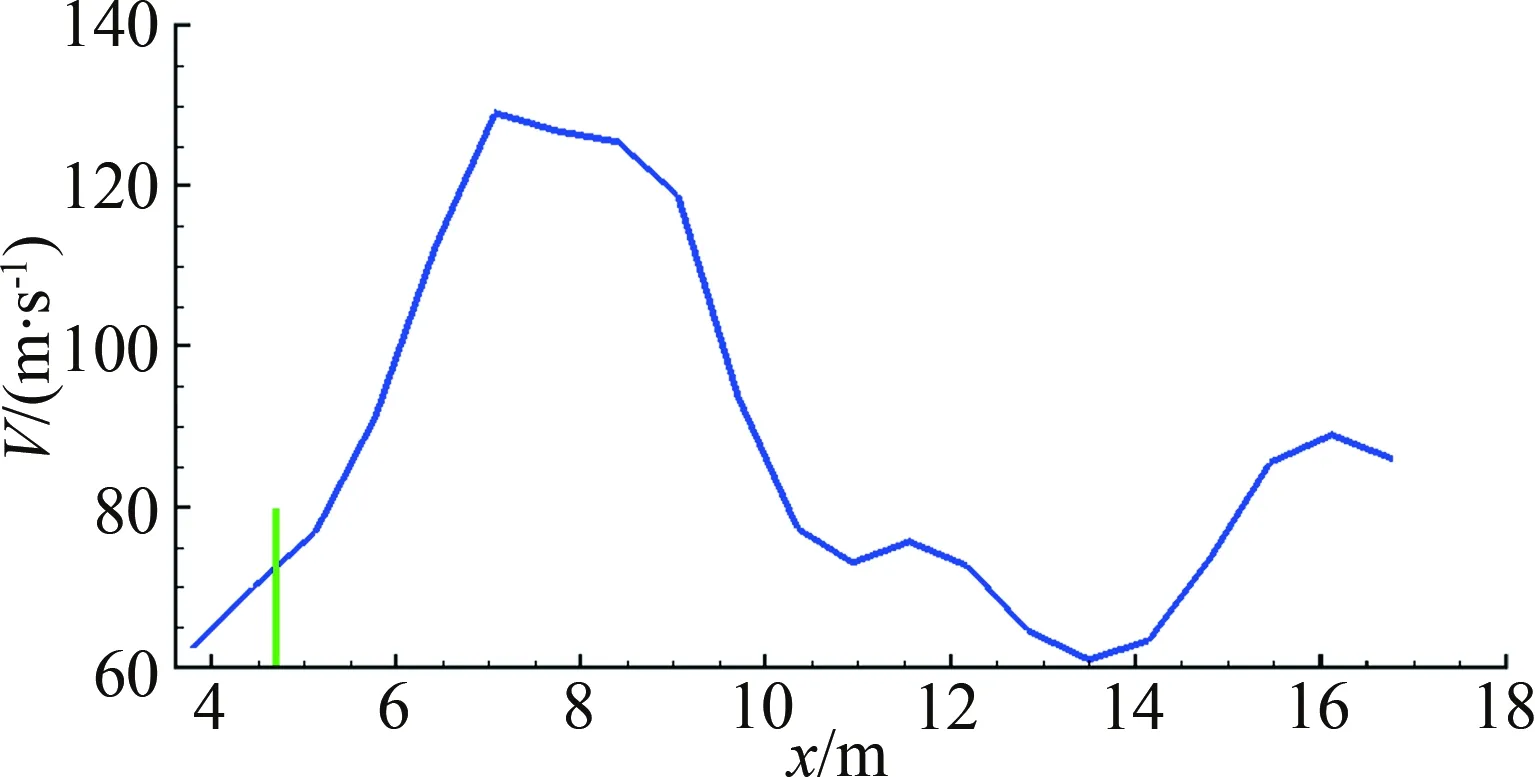
图12 桨盘前后速度分布Fig.12 Velocity distribution before and after the propeller

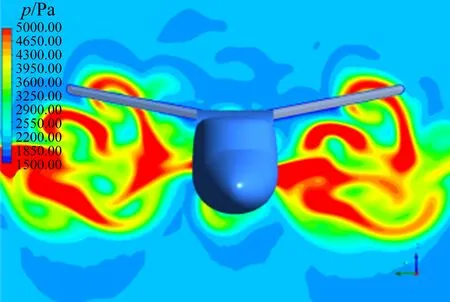
图13和图14给出计算得到的各个迎角下构型A的等总压图和平尾处的总压分布。3000 Pa总压对应的动压约为自由流的1.5倍，5000 Pa时约为自由流的2.5倍。图13和图14中明显看出螺旋桨滑流对构型A的平尾的影响趋势。在各个计算迎角下，大部分的滑流由平尾下部较远处流过，也就是说平尾并没有能够浸没于滑流区。在迎角较小时，高能量的滑流甚至完全位于平尾下方。

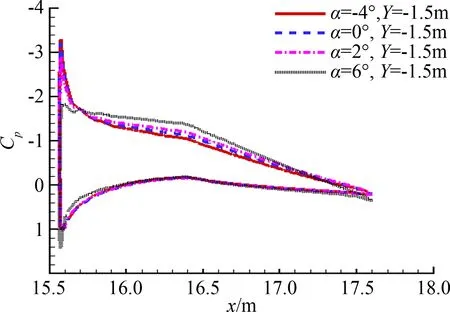
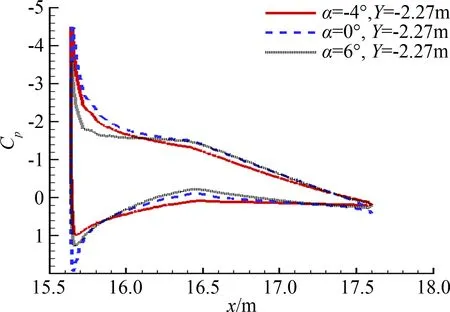
图15和图16给出构型A平尾在±1.5 m和±2.27 m处剖面压力系数的计算结果。可见，螺旋桨滑流对左右平尾的影响差别较大。就本文提取的两个剖面来看，计算结果显示在一定的迎角范围内(-4°～2°)，左侧尾翼表面的压力分布变化较小，亦即该侧平尾产生的俯仰力矩系数变化较小，对纵向稳定性的贡献减弱。右侧两个剖面对迎角变化的敏感度要强于左侧的两个剖面。通过压力系数分布曲线的压力恢复和图17的物面极限流线图可明显看出左右平尾下翼面均保持附体流动，表明此时平尾并非发生负迎角失速。

(a) α=-4°，p0=3000 Pa

(b) α=-4°，p0=5000 Pa

(c) α=0°，p0=3000 Pa

(d) α=0°，p0=5000 Pa

(e) α=4°，p0=3000 Pa

(f) α=4°，p0=5000 Pa

(g) α=10°，p0=3000 Pa

(a) α=-4°

(b) α=0°

(c) α=4°

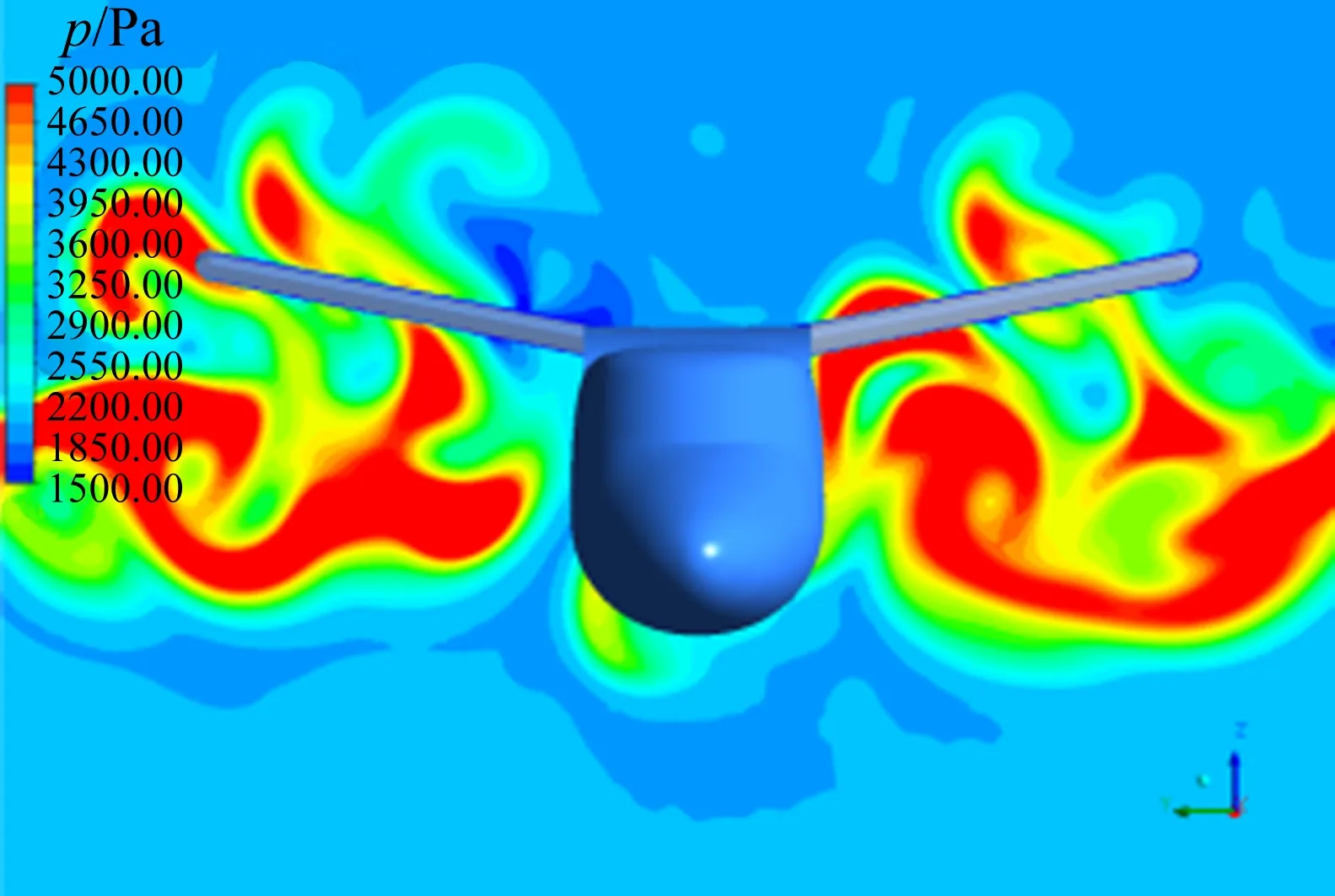
(d) α=10°图14 构型A不同计算迎角下平尾中部的总压分布Fig.14 Total pressure distribution at H-tail of Model A

(a) 左侧平尾

(b) 右侧平尾图15 构型A平尾±1.5 m剖面压力系数分布计算结果Fig.15 Cp distribution at H-tail slices of Model A, Y=±1.5 m

(a) 左侧平尾

(b) 右侧平尾图16 构型A平尾±2.27 m剖面压力系数分布计算结果Fig.16 Cp distribution at H-tail slices of Model A, Y=±2.27 m

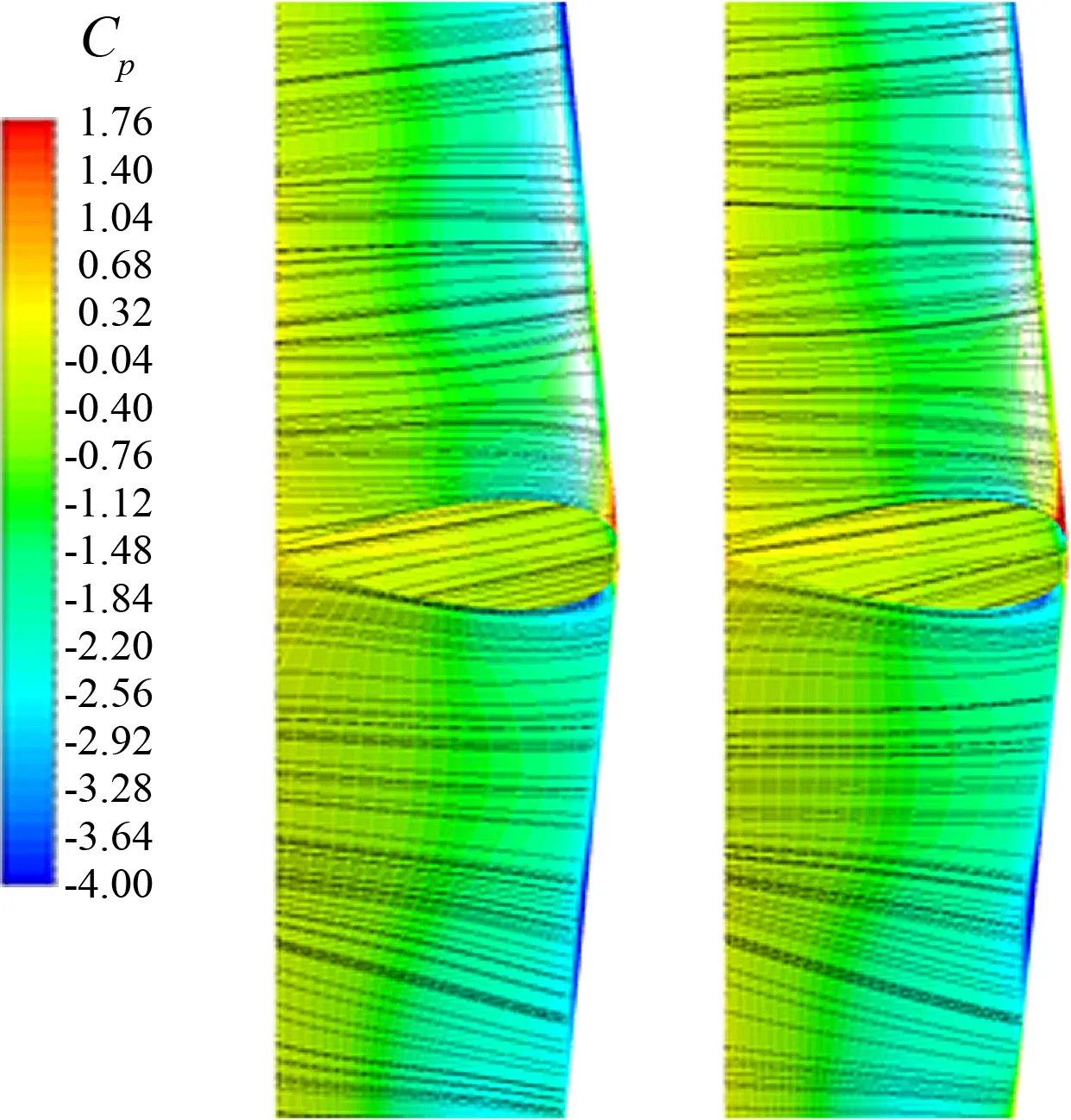
图17 构型A平尾下表面压力云图及 物面极限流线图(左：α=-4°，右：α=0°)Fig.17 Surface streamline and CP distribution at H-tail of Model A (left: α=-4°, right：α=0°)

因此，平尾的气动特性受机翼及襟翼的下洗、飞机迎角、飞机的气动布局特点和螺旋桨滑流及其强度等因素共同影响，构型A在小迎角时的纵向静稳定性下降较多，主要是因为起飞构型升力系数较大引起的下洗影响较强，导致平尾的贡献有所下降，而由于模型姿态导致平尾距离螺旋桨滑流的高能量气流区较远，不能充分利用滑流的有利影响。左右两侧平尾的绕流形态(图14)也能明确看出，在迎角增加时，右侧平尾早于左侧平尾进入滑流区，且由于螺旋桨为逆时针旋转，右侧平尾进入滑流区的面积较左侧平尾为大，使右侧平尾的贡献高于左侧平尾。这也说明，要想改善平尾对飞机纵向静稳定性的贡献，需要使其尽早进入滑流区，充分利用螺旋桨滑流的能量。从飞机气动设计及使用要求来看，很难通过调整襟翼偏度和螺旋桨功率来调整滑流的影响。从飞机布局的角度来看，可以通过调整平尾的位置和/或螺旋桨桨盘的位置，改变平尾和滑流的相对位置，使平尾能够在飞机小迎角时利用螺旋桨滑流的影响。

3.2.3 桨盘和平尾位置的影响

本节针对上文的结论进行初步研究。在构型A的基础上，将螺旋桨上移0.7 m，称为构型B。图18给出构型A和构型B的俯仰力矩特性，可见桨盘上移对飞机小迎角时的纵向静稳定性是略有改善的，而“机身+机翼”以及螺旋桨法向力的力矩曲线变化很小，纵向静稳定性的变化量应当是由于平尾的力矩特性发生改变带来的。图19为两个构型左右两侧平尾俯仰力矩曲线的对比。可以明显看构型B的左侧平尾在小迎角时对纵向静稳定性的贡献增加，右侧平尾也略有改善。在构型A的基础上，将平尾下移0.87 m，称为构型C。图20为A和C两个构型左右两侧平尾俯仰力矩曲线的对比。可见，左侧平尾的俯仰力矩曲线形态改变更为明显，右侧平尾的力矩曲线变化较小，使模型的纵向静稳定性得到改善。这些计算结果也同时表明前文对平尾处流动机理的分析是正确的。更为实际的情况是，涡桨飞机气动布局设计过程中，平尾和桨盘的位置受到各种条件的约束，需要进行更为详尽的组合优化并开展带动力风洞试验验证，以期得到最合适的设计方案。

图18 构型A和构型B俯仰力矩系数分解Fig.18 Pitching moment decomposition of Model A and Model B

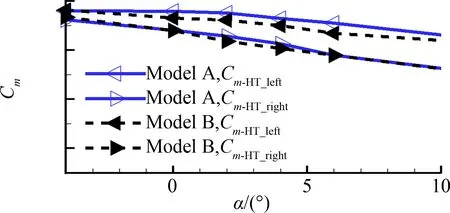
图19 构型A和构型B左右平尾俯仰力矩系数曲线对比Fig.19 H-tail pitching moment of Model A and Model B

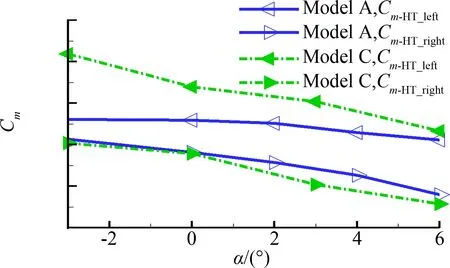
图20 构型A和构型C左右平尾俯仰力矩系数曲线对比Fig.20 H-tail pitching moment of Model A and Model C

4 结 论

本文对某“机身+机翼+襟翼+短舱+平尾”构型进行螺旋桨滑流影响的数值模拟分析，得出如下结论： 1) 螺旋桨直接力使模型的纵向静稳定性降低，且上移螺旋桨对该影响量没有影响；

2) 平尾处的流场是受螺旋桨滑流、机翼下洗和各部件阻滞影响之后产生的复杂流动；

3) 滑流区的高能气流可以提高平尾对纵向稳定性的贡献；

4) 小迎角时，为了提高平尾对纵向静稳定性的贡献，需要使平尾尽早进入滑流区，数值分析表明上移桨盘或者下移平尾可以实现这一目标。

[1]Ouyang S X, Zhao X X, Jiang Z H, et al.The research on wind tunnel test method of propeller’s radial force[J].Journal of Experiments in Fluid Mechanics, 2012, 26(3): 91-94.(in Chinese)欧阳绍修, 赵晓霞, 江宗辉, 等.螺旋桨径向力风洞试验方法研究[J].实验流体力学, 2012, 26(3): 91-94.

[2]Zhao X X.Experiment research of the airflow which surrounds aircraft under the influence of propeller slipstream[J].Aerodynamic Experiment and Measurement & Control, 1995, 9(4): 48-52.(in Chinese)赵学训.螺旋桨滑流对飞机绕流影响的试验研究[J].气动实验与测量控制, 1995, 9(4): 48-52.

[3]Li Z C, Wang X N, Chen H, et al.Experimental research of influence of propeller slipstream on wing flow field[J].Experiments and Measurements in Fluid Mechanics, 2000, 14 (2): 45-48.(in Chinese)李征初, 王勋年, 陈洪, 等.螺旋桨滑流对飞机机翼流场影响试验研究[J].流体力学实验与测量, 2000, 14(2): 45-48.

[4]Liu Y, Zhao X X, Ouyang S X.Investigation on lift stall characteristics of propeller aircraft[J].Acta Aerodynamica Sinica, 2015, 33(5): 655-660.(in Chinese)刘毅, 赵晓霞, 欧阳绍修.螺旋桨飞机升力失速特性研究[J].空气动力学学报, 2015, 33(5): 655-660.

[5]Ren Q Z, Zhao X X, Liu Y, et al.The experimental investigation of slipstream effect on propeller-driven airplane[J].Science Technology and Engineering, 2015, 15(15): 214-217.(in Chinese)任庆祝, 赵晓霞, 刘毅, 等.螺旋桨飞机滑流对全机气动特性影响的试验研究[J].科学技术与工程, 2015, 15(15): 214-217.

[6]Müller J, Aschwanden M, Plaza G A, et al.Wind tunnel simulation of propeller effects in the A400M FLA-4 model[R].AIAA 2005-3706, 2005.

[7]Roosenboom E, Heider A, Schröder A.Propeller slipstream development[R].AIAA 2007-3810, 2007.

[8]Zuo S H, Yang Y.Numerical simulation of propeller/high-lift system interaction[J].Aeronautical Computing Technique, 2007, 37(1): 54-57.(in Chinese)左岁寒, 杨永.螺旋桨滑流对带后缘襟翼机翼气动特性影响的数值分析[J].航空计算技术, 2007, 37(1): 54-57.

[9]RenX F, Yang S P, Duan Z Y, et al.Investigation of the propeller slipstream effects on wing aerodynamic characteristics based on multiple frame of reference[C]//Proceedings of 14th national computational fluid dynamics conference, 2009: 582-585.(in Chinese)任晓峰, 杨士普, 段卓毅, 等.基于多参考坐标系的螺旋桨滑流对机翼气动特性影响分析[C]//第14届全国计算流体力学会议论文集, 2009: 582-585.

[10]Xu H Y, Ye Z Y.Numerical simulation of unsteady propeller slipstream[J].Journal of Aerospace Power, 2011, 26(1): 148-153.(in Chinese)许和勇, 叶正寅.螺旋桨非定常滑流数值模拟[J].航空动力学报, 2011, 26(1): 148-153.

[11]Cheng X L, Li J.Unsteady computational method for the propeller/wing interaction[J].Science Technology and Engineering, 2011, 11(14): 3229-3235.(in Chinese)程晓亮, 李杰.螺旋桨滑流对机翼气动特性影响的方法研究[J].科学技术与工程, 2011, 11(14): 3229-3235[12]Zhang X L, Zhang Y F.Research on interaction of propellerand high-lift system[J].Aeronautical Computing Technique, 2011, 41(4): 1-3.(in Chinese)张小莉, 张一帆.螺旋桨滑流对增升装置气动特性影响研究[J].航空计算技术, 2011, 41(4): 1-3.

[13]Xia Z F, Yang Y.Unsteady numerical simulation interaction effects of propeller and wing[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1195-1201.(in Chinese)夏贞锋, 杨永.螺旋桨滑流与机翼气动干扰的非定常数值模拟[J].航空学报, 2011, 32(7): 1195-1201.

[14]Gong X L, Yang Y, Xia Z F.Unsteady simulation method and actuator disk theory in numerical simulations of propeller′s interference on wing[J].Aeronautical Computing Technique, 2012, 42(1): 76-79.(inChinese)龚晓亮, 杨永, 夏贞锋.螺旋桨滑流与机翼气动干扰数值模拟研究[J].航空计算技术, 2012, 42(1): 76-79.

[15]Zhang L, Bai J Q, Li H X.et al.Research on aerodynamic interference for propeller slipstream over the wing[J].Aeronautical Computing Technique, 2012, 42(2): 87-92.(inChinese)张刘, 白俊强, 李华星, 等.螺旋桨滑流与机翼之间气动干扰影响研究[J].航空计算技术, 2012, 42(2): 87-92.

[16]Yang X C, Wang Y T, Wang G X.et al.Numerical simulation of unsteady propeller slipstream[J].Acta Aerodynamica Sinica, 2014, 32(3): 289-294.(inChinese)杨小川, 王运涛, 王光学, 等.螺旋桨非定常滑流的高效数值模拟研究[J].空气动力学学报, 2014, 32(3): 289-294.

[17]Malard L, Bousquet J M, Atinault O, et al.High speed testing and CFD investigations for the new generation military transport aircraft development[R].AIAA 2005-4744, 2005.

[18]Stuermer A.Unsteady CFD simulations of propeller installation effects[R].AIAA 2006-4969, 2006.

[19]Stuermer A.Unsteady CFD simulations of contra-rotating propeller propulsion systems[R].AIAA 2008-5218, 2008.

[20]Roosenboom E, Stürmer A, Schröder A.Comparison of PIV measurements with unsteady RANS calculations in a propeller slipstream[R].AIAA 2009-3626, 2009.

[21]Xu J K, Bai J Q, Huang J T, et al.Aerodynamic optimization design of wing under the interaction of propeller slipstream[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2910-2920.(inChinese)徐家宽, 白俊强, 黄江涛, 等.考虑螺旋桨滑流影响的机翼气动优化设计[J].航空学报, 2014, 35(11): 2910-2920.

[22]Liu P Q.Air propeller theory and its application[M].Beijing: Beihang University Press, 2006: 152.(in Chinese)刘沛清.空气螺旋桨理论及其应用[M].北京: 北京航空航天大学出版社, 2006.

[23]JI E波果斯拉夫斯基, 著.<八0九> 译校.安-24飞机实用空气动力学[M].北京: 国防工业出版社, 1972.

[24]Obert E D.Aerodynamic design of transport aircraft[M].Shanghai: Shanghai Jiaotong University Press, 2010.(in Chinese)艾德·奧波特, 著.顾诵芬, 吴兴世, 杨新军, 译.运输类飞机的空气动力设计[M].上海: 上海交通大学出版社, 2010.

Numerical simulation of propeller slipstream effects on pitching static stability

REN Xiaofeng*, DUAN Zhuoyi, WEI Jianlong

(AVICTheFirstAircraftInstitute,Xi’an710089,China)

A simple “body+wing+flap+nacelle+propeller+horizontal tail” model (Model A) and two modified ones (Model B and C) were simulated via commercial CFD codes, using unstructured surface matching grid and multi-frame of reference technique to solve Reynolds Averaged Navier-Stokes(RANS) equations.For the simulations, the whole computational domain was divided into three individual domains, namely two rotating domains for the propellers and one stationary domain.The slipstream effects at low speed and in high thrust coefficient condition were studied.It has been demonstrated that the pitching static stability of ‘Model A’ decreases sharply at low angles of attack, while increases slightly at high angles of attack due to the thrust generated by the propellers, the downwash effect of the wing and flap, and the interaction between the slipstream and horizontal tail (H-tail).Generally, the flow field around H-tail of a propeller-driven aircraft is affected by the general layout, the angle of attack, the downwash of the wing and flap, and the slipstream effect.More specifically, the downwash rate of the wing and flap increases due to the slipstream effect, while the efficiency of the H-tail decreases throughout the whole computed range of angles of attack.Since H-tail is not immersed in the slipstream, the high-energy fluid can hardly be utilized to increase its efficiency at low angles of attack.Moreover, it can be seen that the left H-tail contributes to the stability of ‘Model A’ due to the counter-clockwise rotation of the two propellers.

In order to improve the efficiency of H-tail, designers are suggested to modify the relative position between H-tail and the propeller slipstream to make sure that H-tail can be surrounded by high-energy flow generated by the propeller.Moving up the propeller by 0.7 m(Model B) or moving down the H-tail by 0.86m (Model C) has been proved as feasible modifications to increase the pitching static margin at low angles of attack.

propeller; slipstream; pitching static stability; numerical modelling; rotating region; unstructured surface matching grid; multi-frame of reference

0258-1825(2017)03-0383-09

2017-01-04;

2017-02-17

任晓峰*(1982-)，男，安徽寿县人，硕士，高级工程师，主要研究方向：飞机部件气动设计及优化。E-mail：breezeluna@163.com

任晓峰, 段卓毅, 魏剑龙.滑流对飞机纵向静稳定性影响的数值模拟[J].空气动力学学报, 2017, 35(3): 383-391.

10.7638/kqdlxxb-2017.0006 REN X F, DUAN Z Y, WEI J L.Numerical simulation of propeller slipstream effects on pitching static stability[J].Acta Aerodynamica Sinica, 2017, 35(3): 383-391.

V211.4

A doi: 10.7638/kqdlxxb-2017.0006