基于近似模型的空心弹气动外形数值优化
赵 强, 陈志华
(南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094)
基于近似模型的空心弹气动外形数值优化
赵 强, 陈志华*
(南京理工大学 瞬态物理国家重点实验室, 江苏 南京 210094)
作为一种新型超声速弹药,空心弹具有阻力小、精度高等优点,在航空与防空弹药领域具有广阔的发展前景。本文以课题组前期研究的某30 mm空心弹为例,基于四阶多项式响应面近似模型,综合运用UG、ICEM CFD、FLUENT、MATLAB等软件,结合单纯形法,以最小阻力系数为目标对空心弹的气动外形进行了优化,得到了α=0°、Ma=3.0条件下的空心弹最小阻力系数及气动外形参数,该阻力系数与前期数值模拟研究结果相同。在此基础上,以最小阻力系数为目标对α=0°与4°、Ma=2.5~4.0条件下的气动外形进行了优化,得到了相应外形参数的变化范围。另外,利用Kriging近似模型和NSGA-II优化算法等,并以最小阻力系数和最大升阻比为目标,对α=4°、Ma=3.0条件下的空心弹气动外形进行了优化,得到了相应的优化外形。与初始弹形相比,优化后空心弹的气动阻力明显减小。本文验证了近似模型可用于空心弹气动外形优化设计,可为相关工程应用与研究提供重要参考。
空心弹;近似模型;阻力系数;升阻比;优化算法
Keywords: hollow projectile; approximation model; drag coefficient; lift-drag ratio; optimization algorithm
0 引 言
空心弹因其飞行部分是一个中间为空心的薄壁圆管,也被称为管式弹丸,是一种新型超声速弹药。与传统实心弹相比,空心弹具有阻力小、准确度与精度高、成本低、发射武器后坐力小、勤务处理性能更好等优点[1-2],在航空与防空弹药领域具有广阔的应用前景。
早在20世纪70年代,我国和外国就对空心弹开展了广泛的研究,西方主要以应用开发研究及可行性试验为主[3-5],并开发了相应的制式弹药。国内主要对空心弹的研究成果进行了总结以及部分试验验证[6-7]。李惠昌[6]等人结合试验研究情况,详细地叙述了空心弹阻力小、散布精度高与侵彻效果好的特性,给出了阻力系数的近似估算公式,并分析了空心弹的陀螺稳定性;杨金耀[7]对空心弹的风洞试验装置进行了研究。随着CFD技术的发展,对空心弹的气动特性研究主要以流场模拟为主[2,8-9]。李艳玲、陈志华[2]等人利用FLUENT软件对某30 mm空心弹进行了真实条件下的气动特性研究,得到了空心弹的波系结构、压力分布与阻力系数的变化规律;任登凤、谭俊杰[8]等人采用非结构网格的LU-SGS隐式算法计算三维Euler方程,数值模拟了不同马赫数以及不同攻角下的某37 mm空心弹流场,分析了升、阻力特性及流场的波系结构;陈杨、廖振强[9]等人对12.7 mm口径试验弹进行了数值模拟研究,并分析了其外弹道特性。另外,黄振贵、李艳玲[1]等人利用CFD技术,对空心弹不同外形参数条件下的气动特性进行了数值模拟,并利用穷举法对空心弹进行了气动外形数值分析,得到了最小阻力系数的气动外形。
近年来,随着计算机技术的发展,涌现了一大批通用和专用的科学研究和工程应用软件,如工程分析中常用的CAD/CAE/SC类软件,解决了众多领域的科学与工程问题,创造了巨大的经济和社会效益[10]。为了得到空心弹气动阻力系数最小的最优外形,本文运用脚本程序驱动编写的模型更新程序自动实现对UG建立的三维模型的更新,并利用FLUENT对空心弹进行三维流场模拟,得到数值试验结果,并建立近似模型;然后,通过MATLAB编写程序对空心弹基于最小气动阻力系数的气动外形进行优化,得到了与前期研究一致的气动外形,验证了本文方法的可行性。在此基础上,以最小阻力系数为目标,对不同飞行环境下的空心弹气动外形进行了优化,得到了飞行马赫数范围对应的优化外形。最后,以最小阻力系数和最大升阻比为目标对空心弹气动外形进行了优化,得到了相应的优化外形。
1 空心弹气动外形单目标数值优化
本文采用课题组前期研究的三维空心弹模型[1],其二维形式如图1所示。空心弹内喉道面积与入口面积之比必须大于一定值,否则会出现“堵塞”现象[3]。而当内径继续增大时则对气动力的影响不明显,所以本文优化变量没有内径d,仅选择了L1与L2。L1、L2均在20 mm~60 mm的范围变化,且同样仅以最小阻力系数为目标进行优化。对空心弹流场的数值模拟方法与前期工作相同[1],即方程的对流项采用二阶AUSM格式,粘性项采用中心差分格式,时间步进则取二阶R-K格式。

图1 空心弹的基本模型[1](单位:mm)Fig.1 Basic model of a hollow projectile[1](unit:mm)
1.1 近似模型构建
1.1.1 试验设计
采用的试验设计方法是最优拉丁超立方,该方法是对拉丁方设计的改进与优化[15-16]。最优拉丁超立方设计的试验次数可以灵活选择,一般要求试验所包含的有用信息要尽量多,以便于对试验结果进行更好地分析。为了研究L1与L2对阻力系数的影响,建立阻力系数与L1、L2的高精度函数关系,并经过对试验次数的多次尝试、比较,最终确定试验次数为30。
生成数值试验数据的过程如下:(1)通过VBS脚本程序驱动模型更新程序UG_Update.exe,实现三维几何模型参数的更新,提供空心弹和计算域的几何信息;(2)利用VBS脚本程序驱动命令流文件ICEM_CFD.rpl,实现空心弹结构化网格的自动划分;(3)运用VBS脚本程序驱动命令流文件FLUENT.jou,进行空心弹阻力系数计算。30次数值试验的部分结果见表1,与文献[1]的二维结果对比情况如图2~图3所示。

表1 阻力系数的部分数值试验结果Table 1 Partial numerical results of the drag coefficient

图2 外壁阻力系数CD1随L1的变化情况Fig.2 Variation of the outer wall drag coefficient CD1 with L1

图3 内壁阻力系数CD2随L2的变化情况Fig.3 Variation of the inner wall drag coefficient CD2 with L2
由图2~图3可知,三维流场计算的内外壁阻力系数与二维流场计算结果随L2、L1的变化趋势相同。由图2可以看出,三维流场计算的外壁(Wall 1+Wall 2+Wall 3+Wall 4)阻力系数比二维流场计算结果要大,但两者具有较好的平行关系,曲线的最小值点取的L1值较为接近。通过图3,可知L2值在一定的范围内,二维流场计算的内壁(Wall 5+Wall 6+Wall 7+Wall 8)阻力系数要比三维流场得到的结果大,L2超过一定值后,情况则相反;同时,二维流场在内壁阻力取得最小值附近变化非常平缓,三维流场在最小值附近则变化明显,且三维内壁最小阻力系数小于二维内壁最小阻力系数,这是因为三维空心弹内腔的流通性好于二维,应以三维结果为主。
1.1.2 阻力系数近似模型的构建
选用多项式响应面模型来构建阻力系数的近似模型。多项式响应面模型是一种采用统计学回归分析进行函数拟合的近似模型,表达式如下:
(1)
式中,xi是m维自变量x的第i个分量,β0、βi、βij等为未知参数。
当然,也可以考虑用某些适当的函数g(x)来代替式(1)中的x,由此得到的模型可称为广义多项式响应面模型,该模型的数学表达式如式(2)所示:
(2)
式中,函数gi(x)由问题本身的物理性质来确定。
建立的阻力系数的四阶多项式响应面模型的表达式如下:
(3)
若以残差平方和最小作为目标来拟合多项式,最终得到响应面模型的表达式如下:

(4)

1.2 基于近似模型的空心弹阻力系数优化
随着数学规划和计算机技术的完善,对工程系统进行优化设计的技术得到迅速发展并得到实际应用。优化设计中涉及的常常是高维、非线性规划问题,用于求解此类问题的算法有:经典优化方法、全局优化方法、现代优化算法和混合优化策略[17]。在优化过程中,无论是经典优化方法还是智能优化方法,均有其适用范围及优缺点,因此,针对不同的优化问题选择合适的优化方法至关重要。

图4 α=0°、Ma=3.0条件下阻力系数的响应面Fig.4 Response surface for the drag coefficientat α=0° and Ma=3

基于近似模型得到的优化空心弹外形参数与文献[1]中的结果比较接近,验证了利用近似模型进行空心弹气动外形数值优化方法的正确性。与文献[1]中优化结果的差异,主要在于本文采用的数值试验样本是基于三维模型的数值流场得到的计算结果,而文献[1]中的计算结果则基于二维模型,另外网格质量、L1与L2的交互影响和近似模型的精度等因素都会对优化结果有影响。
按照上述方法,同样以最小阻力系数为目标,对空心弹飞行马赫数范围Ma=2.5~4.0、攻角α=0°与4°条件下的气动外形进行了优化,优化的气动外形参数见表2。由表2可以看出,L1和L2分别在45.20mm~51.61mm和39.23mm~42.08mm的范围变化,可根据实际情况(如弹的主要飞行马赫数和空间范围)进行相应的取值。
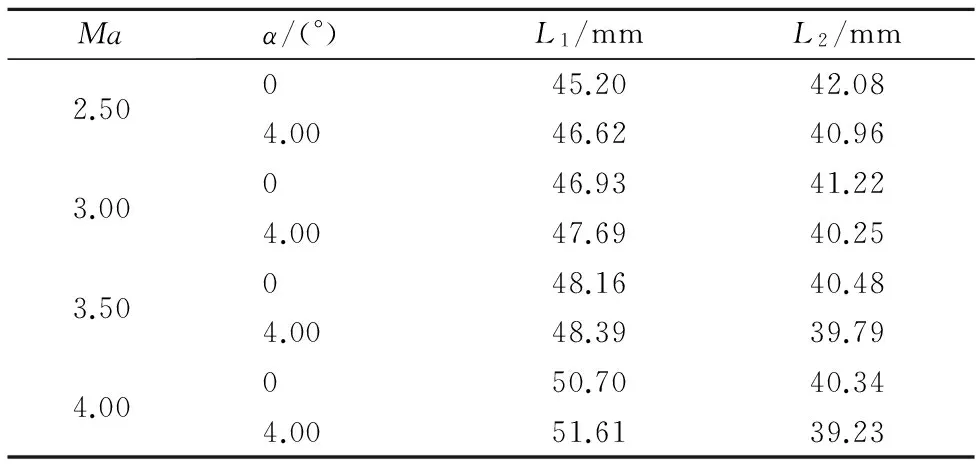
表2 优化的气动外形参数Table 2 Optimized aerodynamic configuration parameters
2 空心弹气动外形多目标数值优化
对于质量一定的空心弹而言(该空心弹模型的体积不随L1、L2的变化而变化),以L1、L2作为优化参数,L1、L2均在20 mm~60 mm的范围变化,以最小阻力系数和最大升阻比作为优化目标对空心弹进行了气动外形优化设计。
2.1 试验设计
直接采用前面验证过程中通过ICEM CFD生成的30组网格,然后运用VBS脚本程序驱动新的命令流文件FLUENT.jou,进行空心弹阻力系数CD与升力系数CL的计算。30次数值试验的部分结果如表3所示。
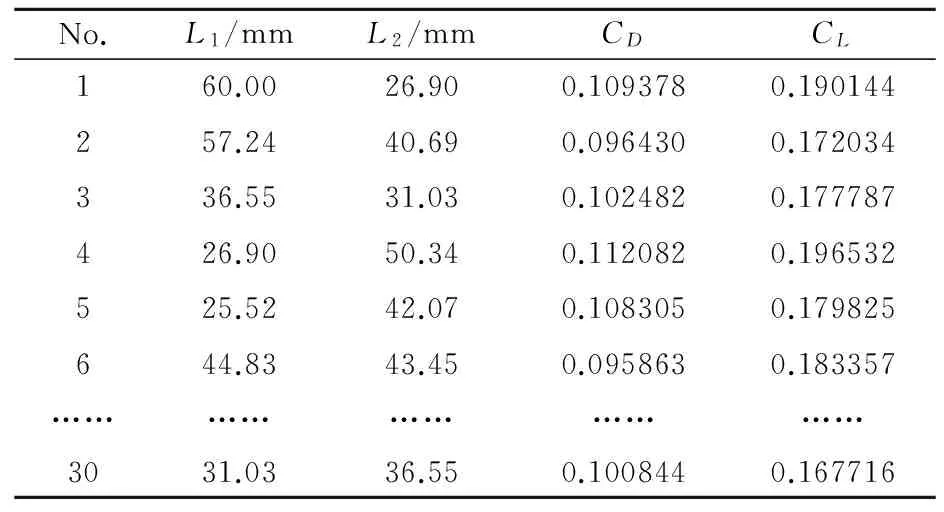
表3 阻力系数与升力系数的部分数值试验结果Table 3 Partial numerical results of the drag and lift coefficients
2.2 近似模型构建
阻力系数仍采用四阶多项式响应面模型,模型的表达式如下:

(5)

对于升力系数,选择Kriging模型来构建其近似模型。Kriging模型是一种基于统计理论、充分考虑变量空间相关特征的插值技术[18],包含回归模型部分与随机模型部分:
(6)
为讨论方便,假定q=1,即一维响应,此时式(6)可以写为:
(7)
式中,回归模型f(x)Tβ提供全局近似,且通常为多项式函数;随机模型z(x)提供局部偏差近似,其均值为零,方差为σ2,协方差为:
(8)
式中,R(θ,w,x)是带有参数向量θ的相关函数,表示训练样本点之间的空间相关性,其表达式为:
(9)
采用的相关函数为GAUSS函数,其表达式如下:
(10)
由无偏条件与预测模型的方差最小条件,可以得出预测点的响应值和均方误差分别为:
(11)
φ(x)=σ2[1+uT(FTR-1F)-1u-
(12)
其中:
β*=(FTR-1F)-1FTR-1Y
r(x)=[R(θ,s1,x)R(θ,s2,x) …R(θ,sm,x)]T
R=[Rij]=[R(θ,si,sj)], (i,j=1,…,m)
u=FTR-1r(x)-f(x)
建立升力系数的Kriging近似模型的过程如下:
(1) 对30个数值试验样本点S及其响应值Y进行按列归一化;

(3) 输出预测点的真实响应值:
式中,sY和mY分别为30个样本点对应的升力系数的标准差和均值。
最终,得到升力系数的响应面和均方误差,分别如图5~图6所示。图5中的散点代表所有样本点,由图可知所有样本点均位于响应面上。

图5 α=4°、Ma=3.0条件下升力系数的响应面Fig.5 Response surface for the lift coefficient at α=4° and Ma=3

图6 α=4°、Ma=3.0条件下升力系数的均方误差Fig.6 Mean squared error(MSE) for the lift coefficient at α=4° and Ma=3
由图6可知,均方误差曲面在某些位置很平缓,数值几乎为0,这些位置在样本点处或离其很近的范围内;而在某些位置会存在一些大的凸起,这些位置距离样本点较远。均方误差越大,表明此预测值波动范围大,预测值的不准确率越高。因此,本文在检验Kriging模型精度的时候,样本点选在了[L1,L2]=[20,20]附近及[L1,L2]=[60,60]附近,检验样本点的情况如表4所示。

表4 6个检验样本Table 4 Six test samples
采用经验累积方差标准[19]来检验Kriging模型的精度,计算公式如下:
(13)
式中,Ngrid为检验样本点总数。由式(13)及表4求得:EISE=5.53×10-6;同时,检验样本点中最大和最小相对误差分别为2.09%和0.07%。
2.3 基于近似模型的空心弹多目标数值优化
采用非支配排序遗传算法(NSGA-II)。NSGA-II由Deb等人于2000年提出[20],是对NSGA算法的改进。在NSGA的基础上加上了精英策略、虚拟适应度策略和快速非支配排序策略,在很大程度上改善了NSGA的计算复杂度较高、无精英策略、需要指定共享半径等缺点,运算速度和鲁棒性得到提高。它存在的不足是难以找到孤立点,此外,当目标数量增加时有可能产生搜索偏移。NSGA-II算法的实现步骤如下:
(1) 初始化种群Pt,t=0;
(2) 从Pt中选择N个个体进入交配池,并对交配池中的个体实施交叉和变异操作,得到新种群Qt;
(3) 合并Pt和Qt得到种群Rt,对其进行非支配排序得到非支配解前端,并进行拥挤度计算,选出其中最好的N个形成下一代种群Pt+1,再进行交叉和变异计算得到Qt+1;
(4) 判断终止条件是否成立,若是,运算停止,输出Pareto解,否则执行步骤(3)。
NSGA-II采用模拟二进制交叉(SBX)[20-21],交叉概率为0.9,交叉分布系数为20;使用均匀变异,变异分布系数为20;种群大小为100;进化代数为250。
通过优化计算得到Pareto最优解集,Pareto前沿如图7所示,同时从Pareto前沿中选取3个设计点,将其列于表5。
由图7和表5可以看出,与初始弹形(L1=20 mm、L2=20 mm,对应的CD=0.14004、CL/CD=1.59746)相比,优化后的空心弹阻力系数和升阻比都得到了一定程度的改善;但过分减小阻力系数或提高升阻比均会使另一目标变坏。理想的空心弹气动外形要求阻力系数最小和升阻比最大,但由于这两者不能同时满足,故必须有所取舍。因此,在空心弹设计时,可根据不同的目标要求进行方案选择,也可结合综合评价方法进行方案选择[22]。同时,本文对3个设计点进行了高精度FLUENT计算,1、2、3号设计点对应的CD和CL/CD分别为0.09439和1.8577、0.09614和1.9269以及0.09831和1.9643;对应的相对误差分别为0.16%和0.23%、0.98%和0.90%以及0.63%和1.17%,进一步验证了近似模型的高精度。
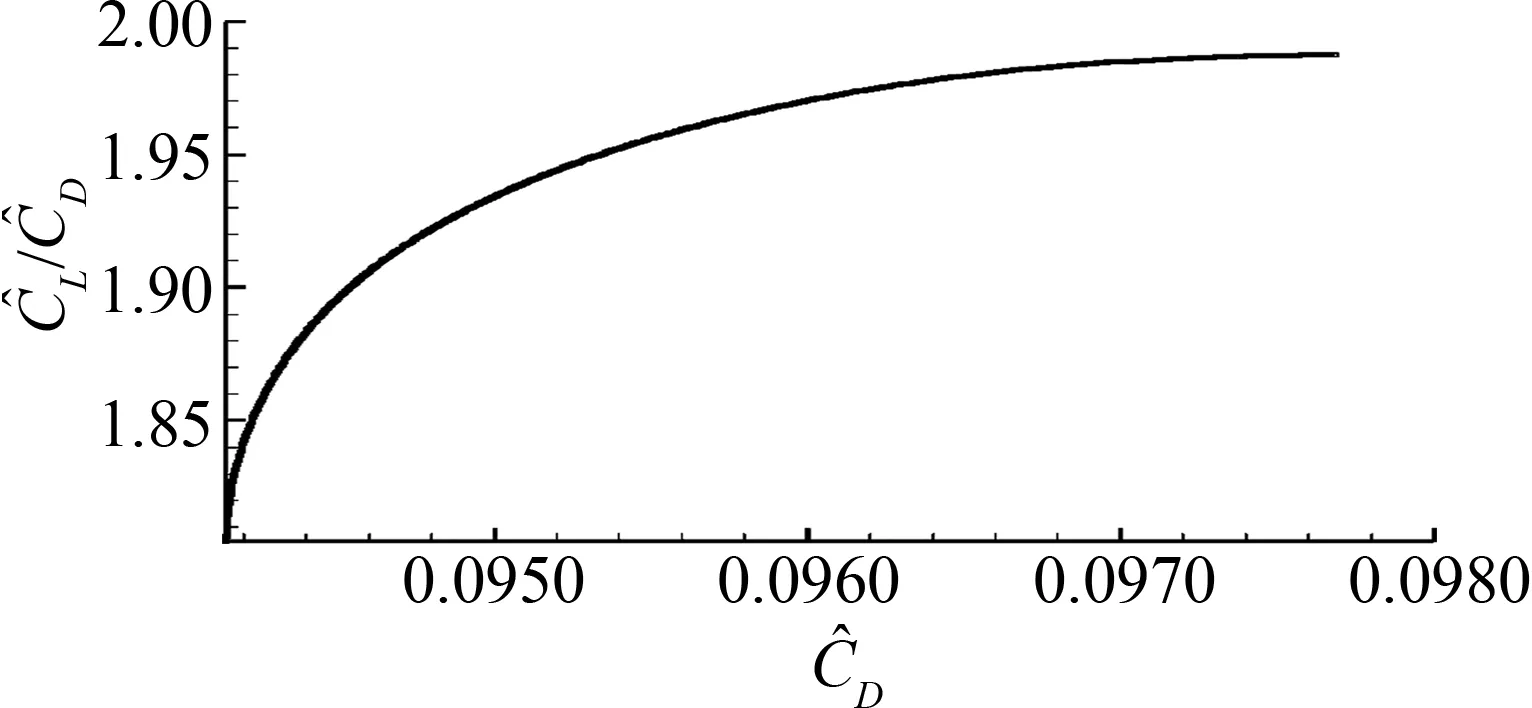
图7 2个目标情况下的Pareto前沿Fig.7 Pareto front under the condition of two objectives表5 3个设计点的对比Table 5 Comparison between three design points

No.L1/mmL2/mmC^DC^L/C^D147.4941.410.094241.8535246.3944.100.095201.9442344.7947.350.097691.9872
3 结束语
本文建立了空心弹阻力系数的四阶多项式响应面模型与升力系数的Kriging模型,并基于近似模型解决了空心弹气动外形的优化设计问题,得到了攻角α=0°、Ma=3.0条件下的最小阻力系数气动外形及攻角α=4°、Ma=3.0条件下阻力系数较小、升阻比较大的空心弹气动外形。同时,本文也基于最小阻力系数对空心弹飞行马赫数范围Ma=2.5~4.0、攻角α=0°和4°条件下的气动外形进行了优化,得到L1和L2的变化范围分别为45.20 mm~51.61 mm和39.23 mm~42.08 mm。充分验证了近似模型可用于空心弹气动外形优化设计。
对优化后的气动外形进行了FLUENT数值验算,所得阻力系数与升力系数和使用近似模型得到的结果相差很小,进一步证明了所建立近似模型方法的可信度。针对空心弹设计优化问题,可进一步结合稳健性设计优化[23](如6 Sigma可靠性鲁棒性设计优化)与多学科设计优化知识等,综合考虑马格努斯效应等,对空心弹气动、弹道、结构(结合结构分析与优化软件MSC/Patran& Nastran)等进行综合设计优化,以进一步提高其整体性能。
[1]Huang Z G, Li Y L, Chen Z H, et al.Numerical investigations on the drag and aerodynamic characteristics of a hollow projectile[J].Acta Armamentarii, 2013, 34(5): 535-540.(in Chinese)黄振贵, 李艳玲, 陈志华, 等.空心弹的阻力特性与气动外形数值分析[J].兵工学报, 2013, 34(5): 535-540.
[2]Li Y L, Chen Z H.Aerodynamic characteristics of hollow projectile with a diameter of 30mm under real conditions[J].Aeronautical Computing Technique, 2011, 41(5): 76-80.(in Chinese)李艳玲, 陈志华.口径30 mm空心弹真实条件下的气动特性研究[J].航空计算技术, 2011, 41(5): 76-80.
[3]Sadowski L M, Malatesta E T, Huerta J.30-mm tubular projectile[R].ADB 087370.US: Army Armoment Research and Development Center Dover NJ Fire Control and Small Caliber Weapon Systems Lab, 1984.
[4]Baxter J E, Cheshire, Poole R D, et al.Tubular projectiles[P].US, 4882997, 1989.
[5]Evans J, Wardlaw A B.Prediction of tubular projectile aerodynamics using the ZUES Euler code[J].Journal of Spacecraft and Rockets, 1989, 26(5): 314-321.
[6]Li H C, Yang J Y, Qi R C.Hollow projectile study[J].Acta Armamentarii, 1980, 2: 33-41.(in Chinese)李惠昌, 杨金耀, 祁荣长.空心弹丸的研究[J].兵工学报, 1980, 2: 33-41.
[7]Yang J Y.Collateral and support device of a hollow projectile in the wind-tunnel experiment[J].Small Arms, 1986, (3): 37-40.(in Chinese)杨金耀.空心弹风洞实验的侧支杆支承装置[J].轻兵器, 1986, (3): 37-40.
[8]Ren D F, Tan J J, Zhang J.Flowfield calculation of hollow projectile using implicit method based on unstructured meshes[J].Mechanics in Engineering, 2006, 28(5): 24-27.(in Chinese)任登凤, 谭俊杰, 张军.非结构隐式方法在空心弹丸流场模拟中的应用[J].力学与实践, 2006, 28(5): 24-27.
[9]Chen Y, Liao Z Q, Wang T, et al.Research on aerodynamic characteristic of hollow projectile with 12.7mm diameter[J].Journal of System Simulation, 2010, 22(2): 337-339.(in Chinese)陈杨, 廖振强, 王涛, 等.12.7mm口径空心弹丸空气动力学特性分析[J].系统仿真学报, 2010, 22(2): 337-339.
[10]Zhu X H, Liao W Z, Huang Y G, et al.CAD/CAE/CFD/VPT/SC software collaboration[M].Beijing: China WaterPower Press, 2004.(in Chinese)祝效华, 廖伟志, 黄永安, 等.CAD/CAE/CFD/VPT/SC软件协作技术[M].北京: 中国水利水电出版社, 2004.
[11]Zhang J, Peng C, Cai C F, et al.Optimization research on combination of spike and forward-facing jet using response surface
methodology[J].Acta Aerodynamica Sinica, 2015, 33(2): 204-210.(in Chinese)张江, 彭程, 蔡琛芳, 等.基于响应面法的带喷流激波针参数优化研究[J].空气动力学学报, 2015, 33(2): 204-210.
[12]Zhang W L, Tan J J, Chen Z H, et al.Optimization of suction control on separation flow around an airfoil at low Reynolds number[J].Acta Aerodynamica Sinica, 2015, 33(6): 757-764.(in Chinese)张旺龙, 谭俊杰, 陈志华, 等.低雷诺数下翼型分离流动抽吸控制优化[J].空气动力学学报, 2015, 33(6): 757-764.
[13]Alexander I J, Forrester, András Sóbester, et al.Engineering design via surrogate modelling[M].UK: John Wiley & Sons Ltd, 2008.
[14]Koziel S, Leifsson L.Surrogate-based modeling and optimization[M].CA: Springer Dordrecht Heidelberg London New York, 2013.
[15]Jin R, Chen W, Agus Sudjianto.An efficient algorithm for constructing optimal design of computer experiments[J].Journal of Statistical Planning and Inference, 2005, 134(1): 268-287.
[16]Queipo N V, Haftka R T, Shyy W, et al.Surrogate-based analysis and optimization[J].Progress in Aerospace Sciences, 2005, 41: 1-28.
[17]Wang Z G, Chen X Q, Luo W C, et al.Research on the theory and application of multidisciplinary design optimization of flight vehicles[M].Beijing: National Defense Industry Press, 2006.(in Chinese)王振国, 陈小前, 罗文彩, 等.飞行器多学科设计优化理论与应用研究[M].北京: 国防工业出版社, 2006.
[18]Yao S B, Guo D L, Sun Z X, et al.Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model[J].Sci China Tech Sci, 2013, 43(2): 186-200.(in Chinese)姚拴宝, 郭迪龙, 孙振旭, 等.基于Kriging代理模型的高速列车头型多目标优化设计[J].中国科学: 技术科学, 2013, 43(2): 186-200.
[19]Rijpkema J J M, Etman L F P, Schoofs A J G.Use of design sensitivity information in response surface and Kriging metamodels[J].Optimization and Engineering, 2001, 2(4): 469-484.
[20]Deb K.An efficient constraint handling method for genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering, 2000, 186: 311-338.
[21]Deb K, Pratap A, Agarwal S, et al.A fast and elitist multiobjective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[22]He F B.MATLAB realization of comprehensive evaluation method[M].Beijing: Science Press, 2010.(in Chinese)何逢标.综合评价方法MATLAB实现[M].北京: 中国社会科学出版社, 2010.
[23]Chen X Q, Yao W, Ou Yang Q.Theory and application of uncertainty-based multidisciplinary design optimization for flight vehicles[M].Beijing: Science Press, 2013.(in Chinese) 陈小前, 姚雯, 欧阳琦.飞行器不确定性多学科设计优化理论与应用[M].北京: 科学出版社, 2013.
Numerical optimization of aerodynamic configuration of a hollow projectile based on the approximation model
ZHAO Qiang, CHEN Zhihua*
(NationalKeyLaboratoryofTransientPhysics,NUST,Nanjing210094,China)
As a new type of supersonic ammunition, the hollow projectile has advantages of low drag and high precision etc., and it has wide applications in aircraft and air defense field.In this paper, based on fourth-order polynomial response surface approximation model, combined with the application of UG, ICEM CFD, FLUENT, MATLAB, etc., and simplex method, the aerodynamic configuration of our previously studied 30mm hollow projectile has been numerically optimized for minimum drag coefficient, and the minimum drag coefficient and optimal aerodynamic configuration parameters were obtained for the hollow projectile at angle of attackα=0° and Mach numberMa=3.0.The minimum drag coefficient has good agreement with our previous numerical result.Based on the same optimal object of minimum drag coefficient, the aerodynamic configuration has been optimized atα=0°, 4°, andMa=2.5~4.0, and the variation ranges of corresponding configuration parameters were obtained.Moreover, by using Kriging approximation model and NSGA-II optimization algorithm etc., based on optimal objects of minimum drag coefficient and maximum lift-drag ratio, the aerodynamic configuration of the hollow projectile has been optimized numerically atα=4° andMa=3.0, and the optimal aerodynamic configuration has been obtained.Compared with the original hollow projectile, the aerodynamic drag force of the optimized one is significantly reduced.It is verified that approximation model can be applied to optimize aerodynamic configuration of a hollow projectile.This study can provide important guidance for relative engineering applications and investigations.
0258-1825(2017)03-0408-07
2015-05-13;
2015-08-04
赵强(1989-),男,山东人,博士研究生,研究方向:弹箭设计及多学科优化.E-mail:zhaoqiangwq123@126.com
陈志华*(1967-),男,湖南人,教授,博士,研究方向:飞行器气动外形与变体优化设计.E-mail: chenzh@mail.njust.edu.cn
赵强, 陈志华.基于近似模型的空心弹气动外形数值优化[J].空气动力学学报, 2017, 35(3): 408-414.
10.7638/kqdlxxb-2015.0056 ZHAO Q, CHEN Z H.Numerical optimization of aerodynamic configuration of a hollow projectile based on the approximation model[J].Acta Aerodynamica Sinica, 2017, 35(3): 408-414.
TJ760.11
A doi: 10.7638/kqdlxxb-2015.0056

