具有标准发生率和脉冲干扰的SIRS模型稳定性分析

马艳丽，李海霞，褚正清，聂东明(安徽新华学院通识教育部，安徽合肥 230088)

具有标准发生率和脉冲干扰的SIRS模型稳定性分析

马艳丽，李海霞，褚正清，聂东明
(安徽新华学院通识教育部，安徽合肥 230088)

本文同时考虑脉冲接种和脉冲剔除策略，建立一个具有标准发生率的SIRS传染病模型，从理论分析和数值模拟方面研究了SIRS传染病模型的动力学性质。首先，得到模型无病T周期解的存在性和疾病流行与否的阈值-基本再生数R0；其次，应用Floquet定理证明了无病T周期解是局部渐近稳定的；然后，利用脉冲微分不等式证明了无病T周期解是全局渐近稳定的；最后，进行计算机数值模拟来进一步验证理论结果的正确性。

SIRS模型；标准发生率；基本再生数；全局渐近稳定性；脉冲微分方程

传染病是人类的健康大敌，世界卫生组织2014年发布《世界卫生统计报告》显示，现在每年新增艾滋病毒感染者约250万，这与20年前的每年300万相比有所下降，但新增感染者仍比死于艾滋病的人数多8万，因此艾滋病人的绝对人数仍在增加.同时，艾滋病对高感染率国家成年人的死亡率产生了重要影响，比如在南非，该国的男性和女性平均预期寿命在1990年均为63岁，但到2011年下降为58岁，另一个非洲国家津巴布韦的人均寿命下降幅度更大，为6岁.近年来，随着环境的污染，如肺结核、性病、禽流感等疾病再次抬头蔓延，而一些新出现的传染病，如艾滋病(AIDS)、传染性非典型肺炎(SARS)等也来势凶猛，全球范围内的传染病防控形势依然严峻.

为了对传染病进行预防和控制，人们常采用免疫接种策略，免疫接种有两种方式：连续接种和脉冲接种.麻疹、病毒性肝炎、脊髓灰质炎等人类长期面对的传染病，常采用连续接种策略.对于突发传染病，如重症急性呼吸综合征(SARS)、流行性感冒等，则适合采用脉冲免疫接种策略.关于脉冲免疫接种模型已有大量文献研究[1-15].剔除也是预防和控制传染病的重要措施，例如人畜共患的传染病禽流感、结核病、破伤风和轮状病毒感染等都可以采取剔除的方法加以控制，关于剔除的传染病模型在文献[16-17]中被研究过.但是将这些预防策略共同考虑的模型鲜见报道，受上述文献[1-17]的启发，本文同时考虑脉冲接种策略和脉冲剔除策略，建立了一个具有标准发生率的SIRS传染病模型，讨论了无病T周期解的局部稳定性和全局稳定性，并利用计算机软件进行了数值模拟.

1 基本模型

模型假设.将种群分为三类：易感者类，记为S(t)，表示t时刻时易感者的数量；染病者类，记为I(t)，表示t时刻时染病者的数量；恢复者类，记为R(t)，表示t时刻时恢复者的数量.b表示出生率；β表示感染率；μ表示自然死亡率；α表示染病者因病死亡率；γ表示染病者到恢复者的转移率；δ表示失去免疫率；p表示比例接种系数；q表示染病者的剔除系数；设b，β，μ，α，γ，δ的值均大于零，T为脉冲周期，根据流行病动力学仓室建模思想建立如下的脉冲微分方程：

(1)

及

(2)

2 模型分析

令N(t)=S(t)+I(t)+R(t)，由方程组(1)和(2)得到关于N(t)的方程

N′(t)=(b-μ)N-αI.

(3)

(4)

及

(5)

N′=(b-μ-εi)N.

因为s+i+r=1，所以仅须考虑下面的方程组

(6)

及

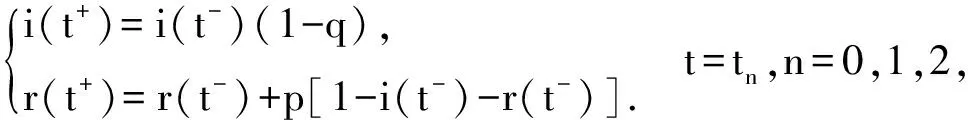
(7)

2.1 无病T周期解的存在性

研究无病T周期解的存在性就是寻找当i=0时，满足方程组(6)和(7)的T周期解．注意到，当i=0时，方程组(6)和(7)变为

其在区间tn≤t≤tn+1上的解为

rn+1=p+(1-p)rnexp{-(b+δ)}.

设F:rn→rn+1是一个映射，满足

rn+1=F(rn)=p+(1-p)rnexp{-(b+δ)}.

该映射有唯一的不动点

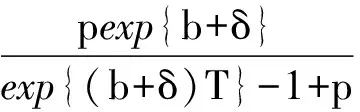
2.2 无病T周期解的稳定性

设Φ(t)是该线性系统的基解矩阵，且满足Φ(0)=I,I为单位阵，基解矩阵为

其中，

φ22(t)=exp{-(b+δ)t},

当t=tn时，得

由Floquet定理得，无病T周期解稳定的充分必要条件是矩阵M的特征值的模都小于1，即只须φ11(T)<1，也就是

定义

则R0是基本再生数，并由上面的讨论可得下面的定理.

定理1 当R0<1时，系统(1)和(2)的无病T周期解是局部渐近稳定的.

定理2 当R0<1时，系统(1)和(2)的无病T周期解是全局渐近稳定的.

为简化定理2的证明，引入如下引理.

引理1 设f(t),g(t)∈C1[0,+)，且则

由方程(1)和(2)的第一个方程得

(8)

对(8)应用微分脉冲不等式可得

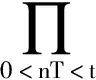
从而有

由方程(1)和(2)的第二方程得

(9)

(10)

对(10)应用脉冲微分方程不等式得

因为

这里

且有

(11)

将式(7)和(8)代入到式(6)可得

(12)

则可以得到

其中

D1(t)是正的且有上界，当R0<1时，有I(t)→0(t→+∞).

事实上，令

则当t≠tn时，有

当t=tk时，

应用微分脉冲等式，由(11)和(12)可得

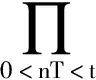
(13)

对于式(13)的第二项，有

综上所述，当R0<1时，无病T周期解是全局渐近稳定的.

3 数值模拟

通过对具有脉冲接种与脉冲剔除的SIRS流行病模型的动力学性态研究，得到了无病平衡T周期解的稳定性.以下用数值模拟当基本再生数R0<1时，系统(1)和(2)的解最终稳定于无病T周期解时的情况，从而验证理论结果的正确性，计算机的模拟结果如图1、图2和图3所示.

图1 R0<1时，易感者人数S随时间t的变化曲线

图2 R0<1时，染病者人数I随时间t的变化曲线

图3 R0<1时，恢复且免疫者人数R随时间t的变化曲线

4 结论与建议

本文同时考虑脉冲接种策略和脉冲剔除策略，建立一个具有标准发生率的SIRS传染病模型，从理论分析和数值模拟方面研究了SIRS传染病模型的动力学性质.通过对模型的稳定性分析，得到了控制疾病再生和消亡的重要阈值——基本再生数R0，证明了无病T周期解的存在性，并证明了当R0<1时，无病T周期解是全局渐近稳定的，疾病最终消亡.通过对具有脉冲接种与脉冲剔除的SIRS流行病模型的稳定性研究，为该类传染病的防治决策提供了理论基础和数量依据.在传染病模型中，考虑疾病发生率为标准发生率，对其他形式的发生率如一般形式接触率或非线性等问题有待进一步研究.

[1]D’Onofrio A. Stability properties of pulse vaccination strategy in SEIR epidemic model[J]. Mathematics Biosciences,2002,179(1):57-72.

[2]Stone L.Theoretical examination of the pulse vaccination policy in the SIR epidemic model[J].Math Modeling,2000,31(4-5):207-215.

[3]章培军,李维德,朱凌峰.SIRS传染病模型的连续接种和脉冲接种的比较[J].兰州大学学报:自然科学版,2011,47(1):82-86.

[4]朱玑,李维德,朱凌峰.基于SIR传染病模型的不同控制策略比较[J].北华大学学报:自然科学版,2011,12(3):15-21.

[5]Jianquan Li,Yanli Yang.SIR-SVS epidemic models with continuous and impulsive vaccination stratgies [J].Journal of Theoretical Biology,2011,280(1):108-116.

[6]Lijie Hao, Guirong Jiang, Suyu Liu,et al.Global dynamics of an SIRS epidemic model with saturation incidence[J].Biosystems,2013,114(1):56-63.

[7]G.P.Samanta.Analysis of a delayed epidemic model with pulse vaccination[J].Chaos,Solitions & Fractals,2014,66(1):74-85.

[8]黄灿云,杨小光,汪训洋.一类具有时滞和双线性发生率的脉冲接种SVIR传染病模型[J].兰州理工大学学报,2012,38(4):131-135.

[9]杨金根,李学志.带脉冲接种和时滞的乙肝模型的稳定性分析[J].数学的实践与认识,2013,12(1):141-149.

[10]Peilin Shi,Lingzhen Dong.Dynamical models for infectious diseases with varying population size and vaccination[J].Journal of Applied Mathematics,2012(1):253-273.

[11]Wenjie Qin,Sanyi Tang,Robert A.Nonlinear pulse vaccination in an SIR epidemic model with resource limitation[J].Abstravt and Applied Analysis,2013(1):24-37.

[12]Pei Yong-zhen,Li Shu-ping,Li Chang-guo,et al.The effect of constant and pulse vaccination on an SIR epidemic model with infectious period[J].Applied Mathematical Modeling,2011,35(8):3866-3878.

[13]Zeng Guang-chao,Chen Lan-sun,Sun Li-hua.Complexity of an SIR epidemic dynamic model with impulsive vaccination control[J].Chaos Solitions and Fractals,2005,26(2):495-505.

[14]Lu Zhong-hua,Cui Xue-bin,Chen Lan-sun.The effect of constant and pulse vaccination on an SIR epidemic model with horizontal and vertical transmission[J].Mathematical and Computer Modeling,2002, 36(9/10):1039-1057.

[15]Helong Liu,Jinyuan Yu,Guangtian Zhu.Global stability of an age-structured SIR epidemic model with impulsive vaccination strategy[J].Journal of Systems Science Complexity,2012,25(3):417-429.

[16]马艳丽,徐文雄,张仲华.具有一般形式接触率的SEIR模型的稳定性分析[J].中国科学技术大学学报,2015,45(1):737-744.

[17]Zhang Zhen,Jin Zhen.Stability properties in an SIR epidemic model with asynchronous pulse vaccination and pulse elimination[J].Journal of Taiyuan Normal University(Natural Science Edition), 2006,54(4):8-10.

Stability Analysis of an SIRS Model With Standard Incidence and Impulsive Perturbations

MA Yan-li,LI Hai-xia,CHU Zheng-qing,NIE Dong-ming

(General Education Department,Anhui Xinhua University,Hefei Anhui 230088,China)

In this paper, impulsive vaccination and impulsive elimination are considered in an SIRS model. The dynamical behavior of an SIRS epidemic model with standard incidence is discussed by means of both theoretical and numerical ways. Firstly, the disease-freeTperiodic solution and the threshold, basic reproductive numberR0which determines whether a disease is extinct or not , are obtained.Secondly, the disease-freeTperiodic solution is locally asymptotically stable by Floquet theorem. Thirdly, the disease-freeTperiodic solution is globally asymptotically stable by impulsive differention in equation. Finally, numerical simulation is given to illustrate the theoretical analysis.

SIRS model; standard incidence; basic reproductive number; global stability; impulsive differention equation

2016-12-30

安徽省高校优秀青年人才支持计划项目“几类具有潜伏期和混合控制策略传染病模型的动力学性态研究”(gxyq2017125)；安徽省高校自然科学重点研究项目“关于常曲率空间中基本凸体的几何不等式理论研究”(KJ2016A310)；安徽新华学院校级自然科学重点研究项目“若干分子图的拓扑指标及其逆问题研究”(2016zr003)；安徽省教学研究项目“以数学建模竞赛为契机——高等数学分层模块化教学在民办应用型本科院校中的探索与实践”(2016jyxm0481)；安徽省精品资源共享课程“高等数学”(2016gxk061)；安徽新华学院校级教学团队“高等数学”(2016jxtdx03)。

马艳丽(1983- )，女，讲师，硕士，从事生物数学研究。

O175

A

2095-7602(2017)06-0001-08