《离散数学》的教学改革与实践研究
杜丽美
(长治学院 计算机系,山西 长治 046011)
《离散数学》的教学改革与实践研究
杜丽美
(长治学院 计算机系,山西 长治 046011)
《离散数学》作为计算机专业的基础必修课,因其内容较为枯燥、乏味,致使学生在学习过程中缺乏兴趣。文章讨论了《离散数学》在今后教学中的改革思路与方法,实践证明这些探讨是具有价值的。
关系;集合运算;邻接矩阵;网络通信
1 引言
《离散数学》是计算机专业中的一门专业基础课,为学生后续专业课比如数据结构、操作系统、计算机网络、数据库技术等的学习提供相关的理论基础知识。
《离散数学》课程中主要包含数理逻辑、集合论、代数系统和图论这四大部分内容,在教学过程中学生普遍认为所讲内容知识点太多、太杂,而且授课形式枯燥、单一,因此大部分学生对该门课程产生了厌学的情绪,并且片面地认为计算机专业的学生将来就是搞编程与操作的,从而忽视了相关理论课程的学习。
2 教学内容的优化和整合
学生对数学类理论课程存在这样的误解,原因之一就是因为理论课程的讲解与计算机的具体操作分离严重,导致学生在学习相关定理、性质时,只是肤浅地记住了文字性的内容,而相关定理或性质的具体应用一概不知,这也是导致学生认为数学课程与计算机学科没有多大联系的很重要的原因之一。
教师在平时的授课过程中,可以有目的地将理论知识和相关应用整合在一起[1-2]。在《离散数学》的授课过程中对于某些知识点教师最好可以给学生演示一下它的实际应用,这样既加深了对理论内容的理解,也激发了大家的学习兴趣[3]。比如数理逻辑这部分内容学完之后,可以给学生介绍一下这部分内容在人工智能方面的应用以及在公务员考试中的应用;集合论这部分内容中集合的运算在关系数据库中的应用;图的矩阵表示中的可达矩阵在网络通信上的应用等。下面就以《离散结构》这门课程为例,来谈谈它在计算机学科中的具体应用[4-6]。
3 集合运算在关系数据库中的应用
数据库中存储的主要对象是二维表,也叫关系。每张二维表都可以看作是一个集合,其中表中的每一个元组为集合中的一个元素(用圆括号括起),因此就将数据库中的表与集合联系了起来。对于数据库中的二维表进行各种交、并、差、选择、投影和连接等运算就可以借助相应集合的运算来加以理解。
对表1和表2进行交、并、差的运算,其实就是进行相应的集合运算:A∩B、A∪B、A-B。若进行如下查询运算:
查询1:查询表1中姓名为“张三”的学生信息。
查询2:查询表1中性别为“女”的学生的姓名。
查询3:对表1和表3进行连接查询。

表1

表2
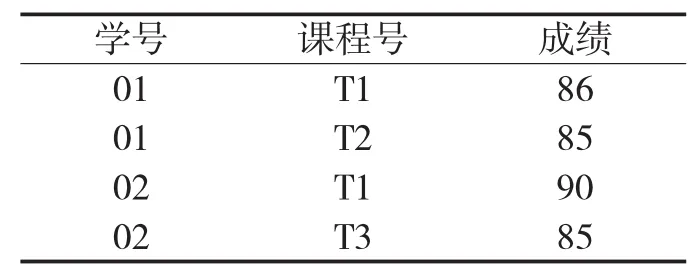
表3
对于以上三种查询,查询1可以看作对集合A作限制运算,查询2可以看作对集合A作像运算,查询3可以看作对集合A与集合C作复合运算,即(其中学号作为公共元素,主表放在前,相关表放在后)。
4 邻接矩阵在网络通信中的应用
对于一个有向图D的邻接矩阵A来说,A中的每个元素表示从结点i到结点j的长度为1的通路的条数。A中所有非零元素相加表示的实际意义为:图D中所有长度为1的通路的总条数。而Ai中的每个元素aij()i表示从结点i到结点j的长度为i的通路的条数,而Ai中所有非零元素相加表示D中所有长度为i的通路的总条数。
为了使学生更加深刻的认识邻接矩阵的以上性质,教师可单网络通信方面的实例促进学生深理解。如图1为8个网络站点之间的通信图,箭头表示通信方向,现问:从站点1出发都能向哪些站点通信且最多经过4个中转站点?

图1 站点之间通信图
首先将图1看作是1个有向图D,然后求出图D的邻接矩阵A为4.1式。
要找到从站点1出发都能向哪些站点通信且最多只能经过4个中转站点,即要求公式4.2的值:

由于A(D)本身阶数比较高,再手动计算A(D)的各次幂显然不现实,所以在这种情况下可以借助matlab来进行计算,计算结果如式4.3所示:

由运行出来的结果可以看到由站点1出发最多经过4个中转站点可以到达的站点为站点2、站点4和站点6。
5 结束语
文章分别从教学内容、教学方法以及教学方式几个方面对《离散数学》进行了研究与探讨,实践证明将两者整合起来的教学效果显著,提高了学生的学习兴趣,活跃了课堂气氛。
[1]杨淑群等.计算机本科专业《离散数学》的教学改革与实践[J].东华理工学院学报,2007,26(2):194-197.
[2]蔺永政等“.离散数学”中实践教学的探讨[J].计算机教育,2006,10:103-104.
[3]徐凤生“.离散数学”课程的教学改革与实践[J].高等理科教育,2009,85(3):44-47.
[4]莫愿斌.凸显计算机专特色的离散数学教学研究与实践[J].计算机教育,2010,12(14):111-113.
[5]陈敏等.离散数学在计算机学科中的应用[J].电脑知识与技术,2009,5(1):251-252.
[6]黄巍等“.离散数学”课程教学改革的探讨[J].中国电力教育,2009(8):82-83.
(责任编辑 张剑妹)
G642.0
A
1673-2014(2017)01-0084-02
2016—12—11
杜丽美(1983— ),女,山西大同人,讲师,硕士,主要从事计算机图形学,图像处理研究。

