Jordan标准形及其过渡矩阵的Jordan链求法

王娇

（长治学院 数学系，山西 长治 046011）

Jordan标准形及其过渡矩阵的Jordan链求法

王娇

（长治学院 数学系，山西 长治 046011）

任何一个矩阵A总是相似于一个与其相应的Jordan标准形，文章就Jordan标准形的过渡矩阵的求法进行了探讨。介绍了矩阵A的根向量，即广义特征向量，并把的Jordan链与根向量一一对应起来，使得求Jordan链组归结为求根向量组。同时，给出根向量组的性质及求法，并总结Jordan标准形和变换矩阵的求法。

Jordan标准形；过渡矩阵；根向量；Jordan链

1 引言

矩阵的Jordan标准形理论在数学、力学和计算方法中得到广泛的应用，因此求矩阵的Jordan标准形和过渡矩阵成为一个重要的研究课题。求矩阵Jordan标准形最常见的方法是初等因子法，然而矩阵的初等因子一般不易求得，实际应用起来有一定难度。至于过渡矩阵，由于它的确定牵涉到复杂的计算问题，在众多的包含矩阵理论的著作中，有些只讨论了矩阵的Jordan标准形而未讨论过渡矩阵的求法，有些给出了算法，但较为繁琐。文章介绍求矩阵Jordan标准形和过渡矩阵的Jordan链[1,2]求解法。

2 Jordan链与根向量

设J是复矩阵A的Jordan标准形，J1（λ0）是J的一个Jordan块，不妨设J=diag（J（1λ0），…）。

由A～J，存在可逆矩阵T，使T-1AT=J，AT=TJ。对J做列分块，设T=（η1，η2，…，ηl，…），则有：

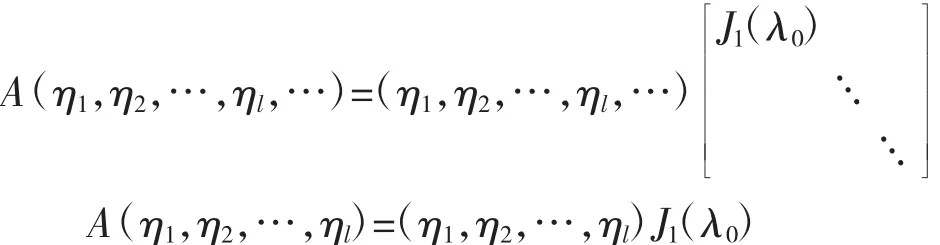
定义1 设是λ0方阵A的特征值，若∃0≠ηi∈Cn,1≤i≤l，使得

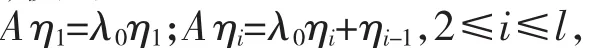
则称有序实数组（η1，η2，…，η）l是方阵A的属于特征值λ0的长为l的Jordan链。

由前面推导，J的每一个Jordan块J（1λ0）都对应于A的一个属于λ0的长为l的Jordan链。反之，A的每一个属于特征值λ0的长为l的Jordan链（η1，η2，…，η）l，都对应Jordan块J（1λ0），使得

这样，就把J的Jordan块与Jordan链一一对应起来，使得求可逆矩阵T归结为求A的Jordan链组。

设（η1，η2，…，η）l是A的属于特征值λ0的长为l的Jordan链，由定义1可得：

定义2 设λ0是方阵A的特征值，若∃ξ∈Cn使得

则称ξ是A的属于特征值λ0的l级根向量。

显然，ξ是A的特征向量当且仅当ξ是A的1级根向量。所以，根向量是特征向量的推广，也称为广义特征向量。前面的推导说明，属于λ0的长为l的Jordan链的最后一个向量是属于λ0的l级根向量。

设ξ是方阵A的属于特征值λ0的l级根向量。

即有（ξ1，ξ2，…，ξ）l是A的属于特征值λ0的长为l的Jordan链。

这样，又把A的长为l的Jordan链与l级根向量一一对应起来，使得求Jordan链组归结为求根向量组。

3 根向量组的性质与求法

定理1[3]设λ0是方阵A的特征值，mA（x）=（x-λ0）kg（x），g（λ0）≠0则A的Jordan标准形中k阶Jordan块个数等于

定理2[3]设λ0是方阵A的特征值，mA（x）=（x-λ0）kg（x），g（λ0）≠0若的第j1，j2，…，jlk个列向量构成列向量组的极大无关组，则C=g（A）的第j1，j2，…，jlk个列向量是A属于特征值λ0的k级根向量，且线性无关。

4 Jordan标准形和过渡矩阵的求法

设λ0是方阵A的m重特征值，则可按下列方法求出属于λ0的若干个根向量，使得它们级数之和为m。

（1）沿用定理2的记号，可按定理2求出lk属于特征值λ0的k级根向量，记为。令，可得lk个长为k的Jordan链。

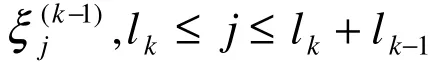
是A的属于特征值λ0的k-1级根向量，且线性无关。令：

是属于λ0的k-2级根向量。仿照（2）又可得到lk-2个属于λ0的长为k-2的Jordan链.

归纳地，可以求出属于λ0的li长为i的Jordan链，1≤i≤k。由Jordan链与Jordan块的对应关系，可得为λ0的代数重数。

5 算例

求可逆矩阵T，使T-1AT=J为Jordan形矩阵，并写出J。

［1］刘江国.广义特征子空间与Jordan链：构造Jordan标准形的一个新途径［J］.郑州工学院学报,1994(03)：76-86.

［2］李伟.关于Jordan链的一种新求法［J］.渤海大学学报(自然科学版),2006(2),134-135.

［3］牛兴文.高等代数与解析几何［M］.北京：化学工业出版社,2005.

［4］王文省等.高等代数［M］.济南：山东大学出版社,2004.

［5］张凯院，徐仲.数值代数［M］，第2版修订本.北京：科学出版社，2010.15-17.

［6］北京大学数学系几何与代数教研室前代数小组.高等代数［M］，第4版.北京：高等教育出版社，2013.

［7］王娇，张凯院，李书连.多矩阵变量线性矩阵方程的广义自反解的迭代算法［J］.数值计算与计算机应用，2013,34(1)：9-19.

（责任编辑 赵巨涛）

O151.21

A

1673-2014（2017）02-0030-03

长治学院校级科研项目（201515）

2017—02—16

王娇（1988— ），女，山东济南人，硕士，助教，主要从事计算数学方向教学与研究。