一种求解Sylvester矩阵方程的松弛梯度迭代方法

王大宽

（山西药科职业学院，山西 太原 030031）

一种求解Sylvester矩阵方程的松弛梯度迭代方法

王大宽

（山西药科职业学院，山西 太原 030031）

本论文提出了一种求解Sylvester矩阵方程的松弛梯度迭代法，并分析了这种迭代方法的收敛性。与已知的梯度迭代方法相比，松弛梯度迭代法提高了梯度迭代方法收敛速度，减少了运算时间。数值例子验证了松弛梯度迭代方法的有效性。

Sylvester矩阵方程；梯度迭代法；收敛性

考虑下面的Sylvester矩阵方程

其中A∈Rm×m，B∈Rn×n，C∈Rm×n是常数矩阵。当B=AT，方程（1）就是所谓的Lyapunov矩阵方程。这些矩阵方程在控制和系统理论中经常出现，并在系统的稳定性分析中扮演着重要角色[1-4]，Ding和Chen[5]利用辨识原理得到了一种求解方程（1）的迭代方法―梯度迭代（GI）方法。Wang等[6]提出了一种改进的梯度迭代（MGI）方法。

本文根据GI方法和MGI方法，给出了一种松弛的梯度迭代方法，并分析了算法的收敛性。我们分别用WT，||W||和t（rW）表示矩阵W的转置、F-范数和迹。对任意的两个矩阵A和B，〈A，B〉=t（rBTA）定义为两个矩阵的内积，并且||A||2=t（rATA）。

1 梯度迭代（GI）方法和改进的梯度迭代（MGI）方法

1.1 梯度迭代（GI）方法

首先我们简单介绍一下求解方程（1）的GI方法，利用辨识原理，定义两个矩阵S1和S2：

分别用X（1k）和X（2k）表示迭代至第k步的近似解,并对这两个迭代值取算数平均，便得到GI算法：

定理1[5]如果Sylvester方程（1）有唯一解X，则由方法（4）得到X（k）的收敛到X，即对任意的初值X（0），都有。

1.2 改进的梯度迭代（MGI）方法

在GI方法中，如果在每一步迭代中利用X（1k）更新X（k-1），便可以得到文献[5]中的MGI方法:

定理2[6]如果Sylvester方程（1）有唯一解X，并且，则由（5）得到的X（k）收敛到X，即对任意的初值X（0），都有。

2 松弛梯度迭代（RGI）方法

在算法（5）中，我们利用X（k-1）和X（1k）来得到新的X（k-1）的值，并引入两个松弛因子ω1和ω2，便得到下面的RGI方法：

定理3 如果Sylvester方程（1）有唯一解X，并且，则由（6）得到的X（k）收敛到X，即对任意的初值X（0），都有。

3 数值例子

我们通过一个数值例子说明RGI方法的有效性，并分别同GI方法、MGI方法和AGBI[7]方法进行比较。

例1 考虑矩阵方程AX+XB=C，其中A,B,C是的60×60矩阵，这些矩阵通过下面的Matlab程序产生：

这里取α=6，这时矩阵方程（1）是很病态的。从图1和表1的数值结果可以看到，RGI方法优于其它三种方法，在收敛速度和运行时间方面比GI方法、MGI方法和AGBI方法更有优势。

图1 四种方法的收敛图像比较

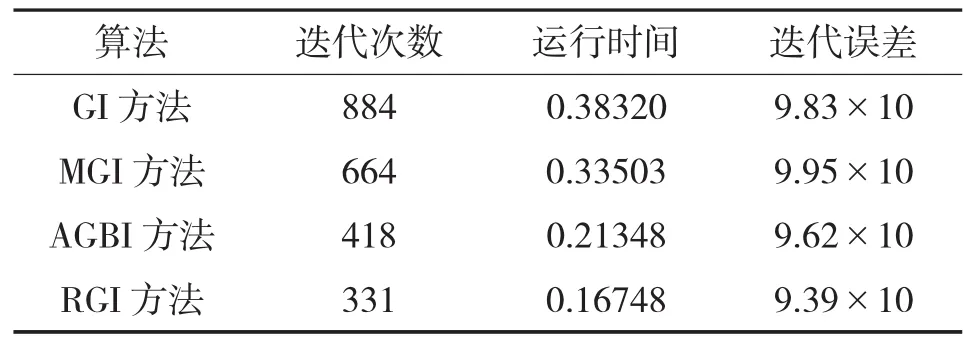
表1 数值结果

参考文献

［1］B itmead R,Explicit solutions of the discrete-time Lyapunov matrix equation and Kalman C Ya kubovich equations［J］.IEEE Trans Autom Control，1981,（26）：1291-1294.

［2］B itmead R,W eiss H,On the solution of the discrete-time Lyapunov matrix equation in controllable canonical form［J］.IEEE Trans Autom Control,1979,（24）：481-482.

［3］丁锋,萧德云，多变量系统状态空间模型的递阶辨识［J］.控制与决策，2005,（20）：848-859.

［4］张凯院，Lyapunov型矩阵方程的迭代-校正解法［J］.纯粹数学与应用数学，1996,（12）：104-108.

［5］Ding F,Chen T W,Gradient based iterative algorithms for solving a class of matrix equations［J］.IEEE Trans A utom Control,2005,（50）：1216-1221.

［6］Wang X,Dai L,Liao D,A modified gradient based algorithm for solving Sylvester e q uations［J］.Appl Math Comput.2012,（218）：5620-5628.

［7］Xie Y J,Ma C F,The accelerated gradient based iterative algorithm for solving a class of generalized Sylvester-transpose matrix equation［J］.A ppl Math Comput,2015,000:1-13.

（责任编辑 赵巨涛）

O13

A

1673-2014（2017）02-0050-03

2017—02—06

王大宽（1969— ），男，山西平遥人，讲师，主要从事高职数学教学与研究。