带有时延的多无人机编队同步控制的策略研究
朱献文,王端(黄淮学院国际学院,河南驻马店463000)
带有时延的多无人机编队同步控制的策略研究
朱献文,王端
(黄淮学院国际学院,河南驻马店463000)
针对带有时延性的多无人机编队同步控制问题,采用拉格朗日方程的控制思想建立无人机编队控制力矩补偿方程策略。首先,建立四旋翼无人机双PID控制系统结构。其次,采用超椭圆方程描述多无人机编队队形,同时根据位置误差与同步误差之间关系设计出的时延性控制力矩。最后,分析了时延性对无人机控制影响以及时延性控制策略对3架无人机编队的同步速度、俯仰角、偏航角性能影响,实验结果表明,时间延迟降低了无人机性能及稳定性;时延性控制策略有效的提升了编队的同步执行能力及稳定性。
编队飞行;拉格朗日方程;无人机;控制策略
0 引言
为了提高无人机的较大操作范围,我们研究了无人机群组编队飞行。对于编队飞行,目前有两种控制策略:集中控制和分散控制。集中控制编队利用计算机技术,是一个简单而单一的地面控制站(Ground Control Station,GCS)连接所有无人机并且直接控制;另一个是分散控制的平面结构,每个无人机的工作负载分开。尽管两种控制方式从根本上不同,但是控制系统都有时间延迟的发生,对无人机飞行性能有着不同影响。集中控制的时间延迟存在于GCS控制太多无人机,过多的操作过程。而分散控制的延迟存在于每一次层次结构之间。文献[1-2]研究中存在系统上的时间延迟问题。系统为了克服操作区域的限制,采用移动网络方式进行通信,然而移动网络在运行过程中产生了大量的时间延迟,致使被控制端失去稳定性。关于较大规模系统与移动互联网络联合运行时,由于移动网络信号通过很多通信节点连接导致通信延迟,因此,时间延迟因素必须作为一种重要影响参数。无人机群组编队控制时,从大型控制系统角度来看,延时预测和几种类型的预测控制[3-4]来解决控制系统的网络延迟问题。文献[7-9]采用不同的控制方法对无人机进行了优化控制,但所有控制算法都未考虑系统的时间延迟问题。
鉴于此,本文针对无人机系统延迟问题,提出了对多无人机编队队形响应的时延性控制策略。首先,建立四旋翼无人机双PID控制系统结构。其次,采用超椭圆方程描述多无人机编队队形,同时根据位置误差与同步误差之间关系设计出的时延性控制力矩。最后,分析了时延性对无人机控制影响以及时延性控制策略对3架无人机编队的同步速度、俯仰角、偏航角性能影响。
1 无人机控制系统结构
1.1 无人机系统组成
无人机系统由三个主要部分组成,如图1所示。包括:无人机(Unmanned Aerial Vehicle,UAV),通信中继服务器(Communication Relay Server,CRS)及地面控制站(Ground Control Station,GCS)。无人机由飞行控制单元(Flight Control Unit,FMU)与各导航传感器包括惯性测量单元(Inertia Measurement Unit,IMU)和全球定位系统(Global Positioning System,GPS)组成。其中,FMU由微控制器和单板计算机构成。通过IMU和GPS信息反馈,微控制器控制无人机的态度和位置。单板计算机负责无人机任务包括:FMU期望轨迹,自检,负载控制,图像处理及轨迹计算等。此外,单板计算机通过移动网络调制解调器及通信中继服务器与其他无人机和GCS通信。
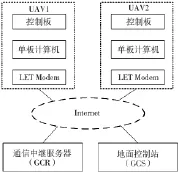
图1 无人机控制结构图
1.2 时间延迟飞行控制系统
无人机飞行控制中,时延性导致无人机飞行的不稳定和运动控制精度降低。特别是无人机群组编队控制时,涉及多数量的无人机在输入和控制之间的自身信息和相互信息传递时会不可避免的产生时间延迟问题[5-6]。此外,在无人机执行任务期间,由于操作员经常手动控制,时间延迟可能导致控制困难,最终造成无人机任务失败。图2为控制原理图(包括时间延迟的控制系统)。参考控制输入PSP和ΨSP作为该方向的期望位置和期望偏航角。在其他方向上,滚转角和俯仰角认为是零,处于稳定控制状态。

图2 时延控制系统原理图
由于远程网络和通信的延缓,导致在发出命令和无人机控制之间的时间延迟。在无人机控制中,两个2 PID控制器串联。方程(1)、(2)描述第一个2PID控制块,方程(3)、(4)描述第二2 PID控制块,分别控制位置和姿态。

式中,P表示位置,ω表示角速度,C1,C2,C3,C4分别表示不同的PID控制器,e1,e2,e3,e4表示每个PID控制器的输入。在两个2 PID控制器之间,沿着每个笛卡尔坐标系的x,y,z轴,倾斜计算器采用加速度的形式计算所需的滚转角和俯仰角。2 PID控制器的输出角加速度及升力计算器输出的升力和转矩传送到无人机动力学模型系统中。
2 无人机编队时延性控制策略
2.1 多无人机编队队形描述
无人机编队采用同步控制方式保持队形及期望的路径轨迹,定义无人机编队满足超椭圆曲线约束,数学表达为:

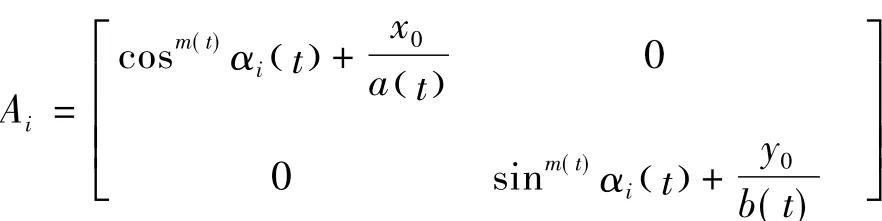
无人机编队同步执行任务,满足约束为:

式中,ci等于Ai-1,pi为无人机位置。
2.2 时延性控制策略
多无人机编队系统通信时延主要是无人机在相互通信时产生,所以只需要考虑无人机编队在同步误差中的延时情况。定义位置的同步误差为:
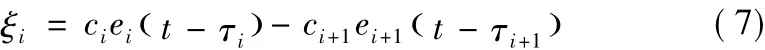
式中,ei为位置误差,即ei=^pi-pi(^pi为理想无人机位置),τi为第i个无人机向无人机传递消息时产生的延时。为了达到理想的无人机运行轨迹,就需要尽量减少位置误差和同步误差,因而定义多无人机编队全局位置误差表示为:

式中,χ为正增益矩阵(0<χ<1)。对公式(8)求导得出=i++χ1)。
为了能简化求解表达式,定义带有位置误差和同步误差的中间变量为:

由公式(17)、公式(18)得到下列关系:

设计出的控制力矩必须满足在t→∞时,同步误差位和置误差收敛到零。无人机编队同步执行任务,需要以全局误差作为调节量。基于拉格朗日方程的控制思想建立无人机编队控制力矩补偿方程为:

式中,λ1,λ2,λ3均为控制参数矩阵,Λi控制系统影响矩阵。
3 实验分析
3.1 时间延迟无人机控制的影响分析
设定的实验条件为:无人机的位置状态表示为X轴、Y轴移动1 m,Z轴移动3 m,时间延迟大约是0.5s,实验参数如表1和表2所示。
图3是时间延迟对无人机控制的影响。

表1 仿真控制参数

表2 仿真惯性矩
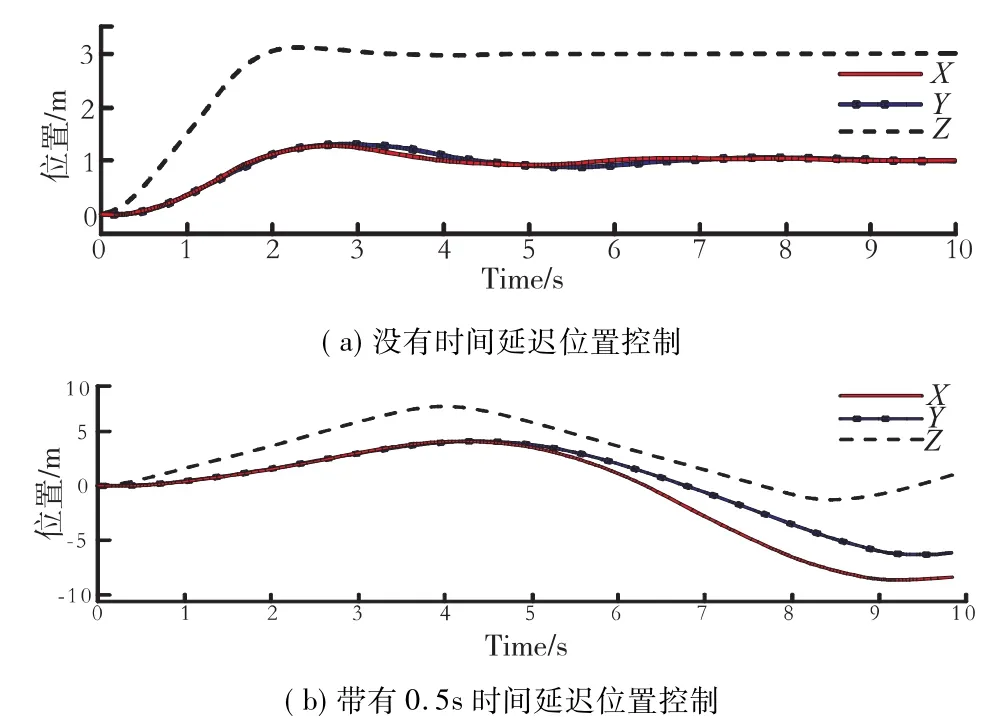
图3时间延迟对无人机控制的影响
图3 a是没有添加延时时间的无人机控制分析,由图可以得出无人机的X方向经过5s后趋于稳定值1.3m,Y方向经过6.4s后趋向1.3m,保持稳定,Z方向经过2.3s后达到3.1m趋于稳定。图3b是系统设置延时为0.5s的实验结果,无人机X、Y、Z方向分别在4.8s,4.8s及4.0s达到最大值(2.8m、2.8m、8.4m),随着时间变化,在10s内无稳定趋势。通过以上结果分析,时间延迟不仅影响了无人机的位置精度而且使无人机的稳定性降低。
3.2 时延控制策略影响分析
为了消除时间延迟对多无人机编队控制的影响,本文采用拉格朗日方程的控制思想建立无人机编队控制力矩补偿方程,解决时延性对无人机控制的影响。为了测试设计控制算法的性能,实验设计了三队无人机编队分别从速度响应,俯仰角响应及偏航角响应三方面验证,编队实验参数如表3所示。

表3 编队仿真参数
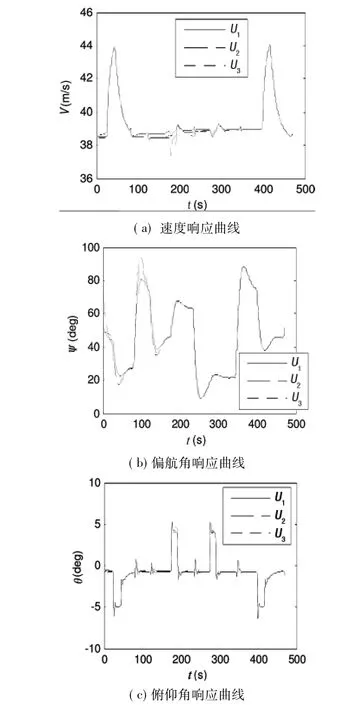
图4 时延控制策略响应曲线
图4是在时延控制策略修正算法下,对3对无人机编队的响应速度,偏航角及俯仰角性能进行了实验分析。操作端在500s内发出不同的控制信号,测试3架编队无人机同步执行任务性能。图4a为速度响应曲线,起始速度都为36m/s,在50s时,三架编队速度同时上升为43.9m/s,在100时降为37m/s,在100s~324s之间,三架无人机速度出现波动,但仍能维持约36m/s保持同步,在400s时,编队速度突增至44m/s,但仍能保持同步。图4b是编队偏航角响应曲线,由图可以看出,编队的偏航角时刻都在放生变化,设置初始偏航角均为43°,在47s时U2,U3的偏航角约为19.8°,而U1约为20.7°,误差为4.3%,在100s时产生最大误差为18%,但在109s时,编队偏航角趋于同步,其他时刻段均保持同步飞行。图4c为编队俯仰角响应曲线,由图上波形可以看出,在极小时间变化内,俯仰角有突增突减情况,但编队成员仍能保持同步俯仰角飞行,能用分说明编队灵敏度高。
通过以上数据分析,编队的速度、偏航角及俯仰角均能基本保持同步,具有一定的稳定性,从而表明时延控制策略提高了无人机编队同步执行性能。
4 结论
针对带有时延性的多无人机编队同步控制问题,提出了控制延时策略,通过分析得出以下结论:
(1)设计带有0.5s时间延迟位置控制实验中,时间延迟使无人机位置处于动荡状态,未能达到设定值。实验表明,时间延迟影响了无人机的位置精度而且使无人机的稳定性降低。
(2)设计了三队无人机编队实验,分别从速度响应,俯仰角响应及偏航角响应分析得出结论,编队的速度、偏航角及俯仰角均能基本保持同步,具有一定的稳定性,从而表明时延控制策略提高了无人机编队同步执行性能。
[1]T X Brown,B Argrow,C Dixon,et al.Ad Hoc UAV Ground Network(AUGNet)[A].AIAA 3rd Unmanned Unlimited Technical Conference,2004.
[2]B R Bellur,M G Lewis,F L Templin.An Adhoc Network for Teams of Autonomous Vehicles[J].Autonomous Intelligent Networks and Systems,2002.
[3]Z Tian,S Li,Y Wang,et al.Networked Control System Time-Delay Compensation Based on Time-Delay Prediction and Improved Implicit GPC[J].Algorithms,2015.
[4]G Ping,Y Xia,D Rees,et al.Design and Stability Criteria of Networked Predictive Control Systems with Random Network Delay in the Feedback Channel”Transactions on Systems,Man,and Cybernetics-Part C[J].Applications and Reviews,2007,37(2):173-184.
[5]K H Han,S Kim,Y J Kim,et al.Implementation of Internet-Based Personal Robot with Internet Control Architecture[C].Robotics&Automation,2001:217-222.
[6]梁慧慧.带有时延的多机器人编队路径追踪和同步控制的策略研究[D].哈尔滨:哈尔滨工业大学,2013.
[7]袁利平,陈宗基,周锐,等.多无人机同时到达的分散化控制方法[J].航空学报,2010,31(4):797-805.
[8]周绍磊,周超,陈洁.基于预测控制方法的UAV视觉编队飞行控制律设计[J].电光与控制,2013,20(1):9-13.
[9]袁亮,楚仕彬.基于卡尔曼滤波的无人机姿态测量研究[J].组合机床与自动化加工技术,2015(7):110-117.
[10]王晓光,章卫国,陈伟.无人机编队超视距空战决策及作战仿真[J].控制与决策,2015,30(2):328-334.
(编辑李秀敏)
Study on Synchronization Approach to Formation Control in Multi-UAVs with Time Delay
ZHU Xian-wen,WANG Duan
(International College,College of Huanghuai,Zhumadian Henan 463000,China)
For the Synchronization approach to formation controlin multi-UAVs w ith time delay,the control strategy of torque compensation in UAV formation based on the control idea of Lagrange equation is proposed.Firstly,the double PID control system structureof four rotorcraft UAV is built.Secondly,the Multi-UAV formation is described by the super elliptic equations and the control torque is designed based on the relation between position error and synchronization error.Finally,the control impact factor of UAV is analyzed and the performance of the control strategy of three drones formation in synchronous speed,pitching angle and yaw angle is analyzed.The experimental results show that the UAV performance and stability would be reduced due to the time delay;The synchronous execution ability and stability of the formation are improved effectively by the control strategy.
formation flight;lagrange equation;UAV;control strategy
TH166;TG506
A
1001-2265(2017)04-0078-04
10.13462/j.cnki.mmtamt.2017.04.019
2016-08-01
国家自然科学基金(31570515)
朱献文(1981—),女,河南驻马店人,黄淮学院讲师,硕士,研究方向为人工智能、智能算法、移动开发,(E-mail)zhu.x.w@163.com。

