重积分换元定理的简易证明

林庆泽， 林羲行

(1. 广东工业大学 应用数学学院, 广东 广州 510520；2. 广州大学 物理与电子工程学院, 广东 广州 510006；3. 北京大学 数学科学学院, 北京 100871)



重积分换元定理的简易证明

林庆泽1,2， 林羲行3

(1. 广东工业大学 应用数学学院, 广东 广州 510520；2. 广州大学 物理与电子工程学院, 广东 广州 510006；3. 北京大学 数学科学学院, 北京 100871)

利用曲线微分向量及其相关的代数概念，如内积和外积，给出重积分换元定理的一种更简易的证明：证明二重积分换元定理；用同样的方法证明三重积分换元定理；根据行列式的几何意义给出n重积分换元定理的简易证明.

重积分换元定理； 微分向量； 内积； 外积

MSC 2010:26B15

0 引 言

对于一般的论文或书籍[1-4]，多重积分换元定理的证明过程较难理解.文献[5]对重积分换元公式中雅可比行列式的几何含义做了详细的阐述.本文受文献[5～6]的启发，从代数运算角度出发，以曲线微分向量[7]为工具，利用其相关的代数概念，如内积和外积[8]，给出多重积分换元定理的一种较为简易的证明：首先证明二重积分换元定理；接着用同样的方法证明三重积分换元定理；最后在以上两个直观证明的基础上，根据行列式的几何意义给出抽象n重积分换元定理的简易证明.

1 二重积分换元定理的证明

(i)Ψ在Δ2上是连续可微的；

则下面的等式成立：

(1)

(2)

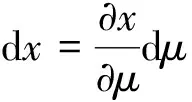
(3)

因此，区域Δ1上的面积元为：

(4)

故可推出：

(5)

2 三重积分换元定理的证明

(i)Ψ在Δ2上是连续可微的；

则下面的等式成立：

(6)

证明 同定理1的证明一样，对于参数ν和τ皆为常数的空间曲线Ψ，则

且

所以

(7)

对于参数μ和τ皆为常数的空间曲线Ψ，则

且

所以

(8)

对于参数μ和ν皆为常数的空间曲线Ψ，则

且

所以

(9)

因此，区域Δ1上的体积元为：

(10)

故可推出：

3 n重积分换元定理的证明

(i)Ψ在Δ2上是连续可微的；

则下面的等式成立：

(11)

证明 同定理2的证明一样，如果参数μ2,…,μn皆为常数的空间曲线Ψ，则

所以

(12)

类似地考虑其它空间曲线，则得到：

(13)

其中：k=1,…,n.

因此，根据行列式的几何意义，区域Δ1上的体积元为：

(14)

故可推出：

[1]华东师范大学数学系.数学分析：下册[M].北京:高等教育出版社,2010.

[2]华罗庚.高等数学引论：第二分册[M].北京: 高等教育出版社,2009.

[3]陈纪修,於崇华,金路.数学分析：下册[M].北京:高等教育出版社,2004.

[4]ZORICHVA.MathematicalAnalysis[M].Berlin:Springer-Verlag,2004.

[5]汪惠鑫.重积分换元中Jacobians的几何含义[J].北京化工学院学报(自然科学版),1988,15(2):119-125.

[6]陆宜清.浅谈重积分的换元积分法[J].南阳师范学院学报,2015,14(6):46-49.

[7]郑崇友,王汇淳,侯忠义,等.几何学引论[M].北京:高等教育出版社,2006.

[8]华罗庚.高等数学引论：第一分册[M].北京:高等教育出版社,2009.

MSC 2010:26B15

[责任编辑 高俊娥]

A Simple Proof of Multiple Integral Substitution Theorem

LIN Qingze1,2, LIN Xixing3

(1.School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China; 2. School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China; 3. School of Mathematical Sciences, Peking University, Beijing 100871, China)

By using curve differential vectors and their related concepts, such as inner products and exterior products, a simpler proof of the theorem would be given. This paper first proves the Double Integral Substitution Theorem, and then proves the analogous theorem of the Triple Integral in the same way. Finally, according to the geometrical meaning of determinant, then-dimentionalintegralsubstitutiontheoremisproven.

the multiple integral substitution theorem; differential vector; interior product; exterior product

2017-02-20 通信作者:林庆泽，硕士，研究方向：数学与物理学.E-mail：gdlqz@e.gzhu.edu.cn

O

A

1009-1734(2017)04-0008-04