基于双三次Bezier曲面在球体建模中的应用

孔令德 康凤娥

(太原工业学院 山西 太原 030008)

基于双三次Bezier曲面在球体建模中的应用

孔令德 康凤娥

(太原工业学院 山西 太原 030008)

传统球体建模的几何元素是由非参数表示的数学方程生成，建模过程繁琐，不易形变生成其他模型。针对这些不足，提出基于双三次Bezier曲面的球体建模方法。采用de Casteljau细分算法，反求圆和椭圆的双三次Bezier曲面的控制点，获得了影响Bezier曲面控制点的魔术常数，给出了球体双三次Bezier曲面的控制点坐标，实现了基于三次Bezier曲面的三维球体、椭球体网格模型的绘制。通过调整控制点参数，生成了类似蛋形体以及苹果体等曲面体网格模型。实验结果表明，魔术常数为计算旋转体模型的控制点提供了新的技术支持，Bezier方法进行三维建模具有很强的设计灵活性和实用性。

计算机应用 双三次Bezier曲面 de Casteljau细分算法 控制点

0 引 言

Bezier曲线曲面因便于设计者操作，因此广泛应用于航空航天、模具、汽车外形等各种复杂曲面的设计中，例如汽车的引擎罩、轮船的船体，日常生活中的苹果、鸡蛋等。Bezier曲线由法国雪铁龙(Citroen)汽车公司的De Casteljau于1959年发明，但作为公司的技术机密，直到1975年之后才引起人们的注意。1962年法国雷诺(Renault)汽车公司的工程师Bezier独立提出了曲线曲面。其优点是曲线曲面参数化表示脱离了对坐标的赖，其构造简单直观、易于显示和控制，给设计者带来了极大的方便，已经成为CAD中用于描述形状信息的主要工具。

在工程应用中，对于圆弧的造型方法有多种，如中点生成椭圆的整数型算法[1]、双步圆的反走样生成算法[2]、利用残差控制的快速圆弧生成与反走样算法[3]等。这些曲线是由已知曲线的非参数表示的数学方程生成的，与非参数表示相比，参数表示的曲线曲面更能满足形状数学描述的要求[4]，Bezier曲线曲面就是一种以逼近为基础的参数曲线曲面。近年来，国内有诸多学者对基于Bezier曲线表示的圆弧已有研究。杭后俊等[5]通过引入一个可在一定范围内变化的参数，得到同一圆弧不同标准型有理三次Bezier表示；储理才等[6]研究了误差函数有5个相异零点的情形,给出圆弧的四次Bezier曲线控制顶点的计算公式, 误差的解析表达式和逼近阶；尤伟等[7]为了解决由Bezier曲线上型值点反求控制点矩阵求逆的大运算量问题,提出了先把。数目较多的一组型值点按序分解成几组数目较少型值点,再把这几组型值点逐个生成控制点,这样把一个高阶矩阵求逆转化为几个低阶矩阵的求逆。上述学者较多是在已知控制点的前提下对曲线表达式进行研究，但是Bezier曲线从一开始就面向几何而不是面向代数的，著名Utah Teapot就是面向几何用双三次Beizer曲面建模的一个经典例子[8]。只有将函数逼近与几何表示结合起来，才能使得设计者在工程设计中更加直观地观察到所给条件与设计曲线之间的关系，通过调整控制点参数灵活方便地设计出所希望的形状。

本文以球体，椭球体为研究对象，从构建双三次Bezier曲面控制点出发，采用de Casteljau细分算法，解得一个影响控制点参数的魔术常数，给出了球体双三次Bezier曲面的控制点坐标，其他卦限控制点坐标可对称获得。实现了用双三次Bezier曲面绘制三维球体、椭球体网格模型，调整控制点参数实现生成鸡蛋体以及苹果体等网格模型，绘制图形光滑拼接，充分显示了用参数Bezier曲线曲面表示曲面体的设计灵活性。

1 De Casteljau细分算法描述

De Casteljau细分算法其构造思想是从一个控制多边形或者控制网格出发,按一定的细分规则插入新顶点,再连接这些新顶点得到新控制多边形或控制网格,将所得新控制多边形或控制网格再作为初始控制多边形或控制网格，重复上述细分过程,这样循环细分下去,控制多边形或控制网格就被逐渐加细,其极限成为一条曲线或一张曲面[9]。

给定空间n+1个控制点Pi(i=0，1，…,n)及参数t，DeCasteljau细分算法表述为：

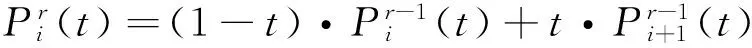
(1)

DeCasteljau算法的几何作图是在线段P0P1上选择一个点P(t)，使得P(t)点划分P0P1为t:(1-t)两段，如图1所示。给定点P0、P1的坐标以及t的值，点P(t)的坐标为P(t)=P0+t(P1-P0)=(1-t)P0+tP1，t∈[0,1]。

图1 De Casteljau算法基础

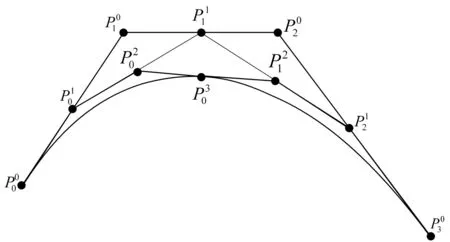
图2 细分过程

2 De Casteljau细分算法反求圆弧控制点

Bezier曲线曲面因方便设计者操作而广泛应用于各种复杂的曲面造型中，Bezier曲线曲面是通过其控制点定义的,有关Bezier曲线曲面造型的算法也都是在已知控制点的前提下描述的，而在Bezier曲线曲面的设计中，首先要知道控制点的的准确位置，这在造型设计中有着重要意义。下面将以三次Bezier逼近圆弧为例，说明采用deCasteljau细分算法，获得影响控制点参数的一个魔术常数。

2.1 反求圆弧的三次Bezier控制点

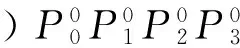
(2)

图3 三次Bezier曲线逼近1/4圆

(3)

根据圆的对称性可绘制圆的其它3段三次Bezier曲线，显然，每两段Bezier曲线达到了G0连续：第一段三次Bezier曲线的终止点是第二段三次Bezier曲线的起点；同时达到了G1连续：连接点处与相邻两侧的控制点三点共线，且与连接点相邻的两控制点位于连接点的两侧，因此一个整圆的四段三次Bezier曲线实现了光滑拼接。

2.2 反求椭圆的三次Bezier控制点

同反求圆的控制点方法类似，建立如图4所示的坐标系，将椭圆弧分成4个部分，用一段三次Bezier曲线逼近1/4椭圆弧。

图4 三次Bezier曲线逼近1/4椭圆

b2x2+a2y2-a2b2=0

(4)

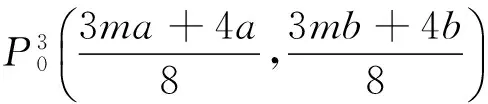
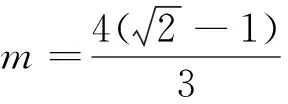
在同一坐标系，使用四段三次Bezier曲线绘制一个红色圆(椭圆)曲线，再使用MFC绘图函数在同一圆心，以相同的半径绘制一个蓝色的圆(椭圆)曲线，结果显示，两种方法绘制的图形完全重合。

3 建模技术实例

3.1 球的双三次Bezier曲面控制点算法

建立如图5所示的坐标系，直角坐标系的坐标轴将球分为8个卦限，每个卦限的球面用一张双三次Bezier曲面表示，逆时针方向、由上至下依次拼接8张曲面完成实现Bezier方法绘制一个完整球体表面。

图6为第一卦限球的双三次Bezier曲面的16个控制点，其中位于Bezier曲面片一边的01、10、20、30四个控制点退化为一个点。将上述二维坐标系下反求1/4圆控制点的方法，应用到求解三维坐标系下两组正交的三次Bezier曲线控制点。方法是:先求双三次Bezier曲面的四个角点坐标，然后利用魔术常数为影响因子，通过角点坐标计算曲线的另外两个控制点坐标值。

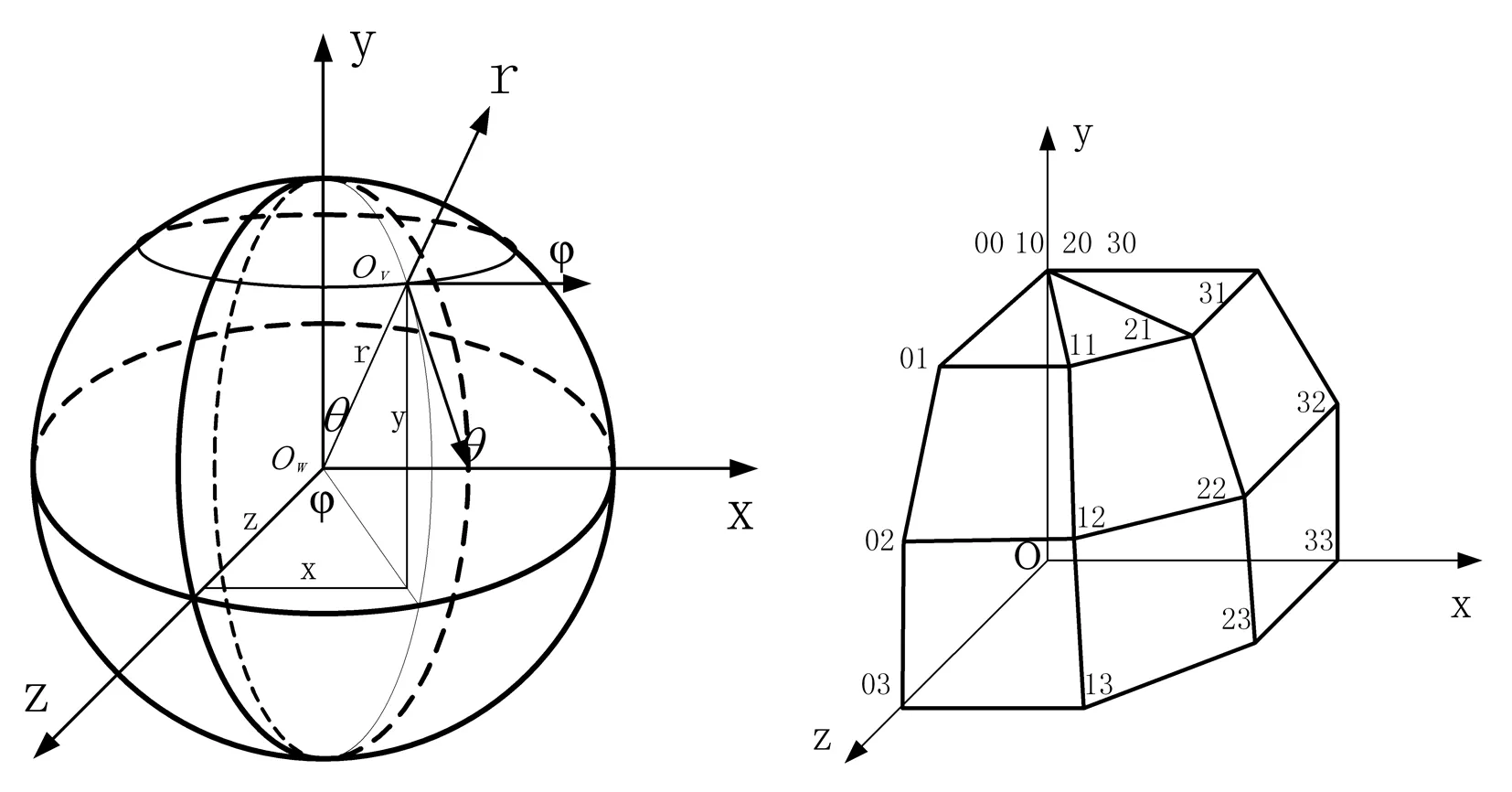
图5 直角坐标系与球坐标系 图6 Bezier曲面的控制点

为了便于计算和程序实现，将曲面控制点用球坐标表示，如图6所示，r为球面Ov点到球心Ow之间的距离，r与y轴的夹角为，r在xOwz面投影线与z轴的夹角为φ，则Ov点的球坐标与笛卡尔坐标的关系为：

(5)

由于双三次Bezier曲面的四个角控制点00、03、30、33位于球的表面，因此它们的坐标值用球坐标表示为：

对于位于球面之外的Bezier曲面的控制点坐标，可以通过魔术常数m作为曲面四个角点的影响因子加以计算获得。计算顺序为：通过00和03角点计算出01和02控制点，30和33角点计算出31和32控制点，03和33角点计算出13和23控制点，然后再用控制点01和31计算出11和21控制点，由02和32控制点计算出12和22控制点，至此第一卦限三次Bezier曲面的16个控制点全部求出，用同样的方法获得其他卦限曲面的控制点坐标。

限于篇幅下面给出第一卦限双三次Bezier曲面片的控制点坐标,见表1所示，其中m为魔术常数。其他卦限的控制点坐标可根据球的对称性求得。

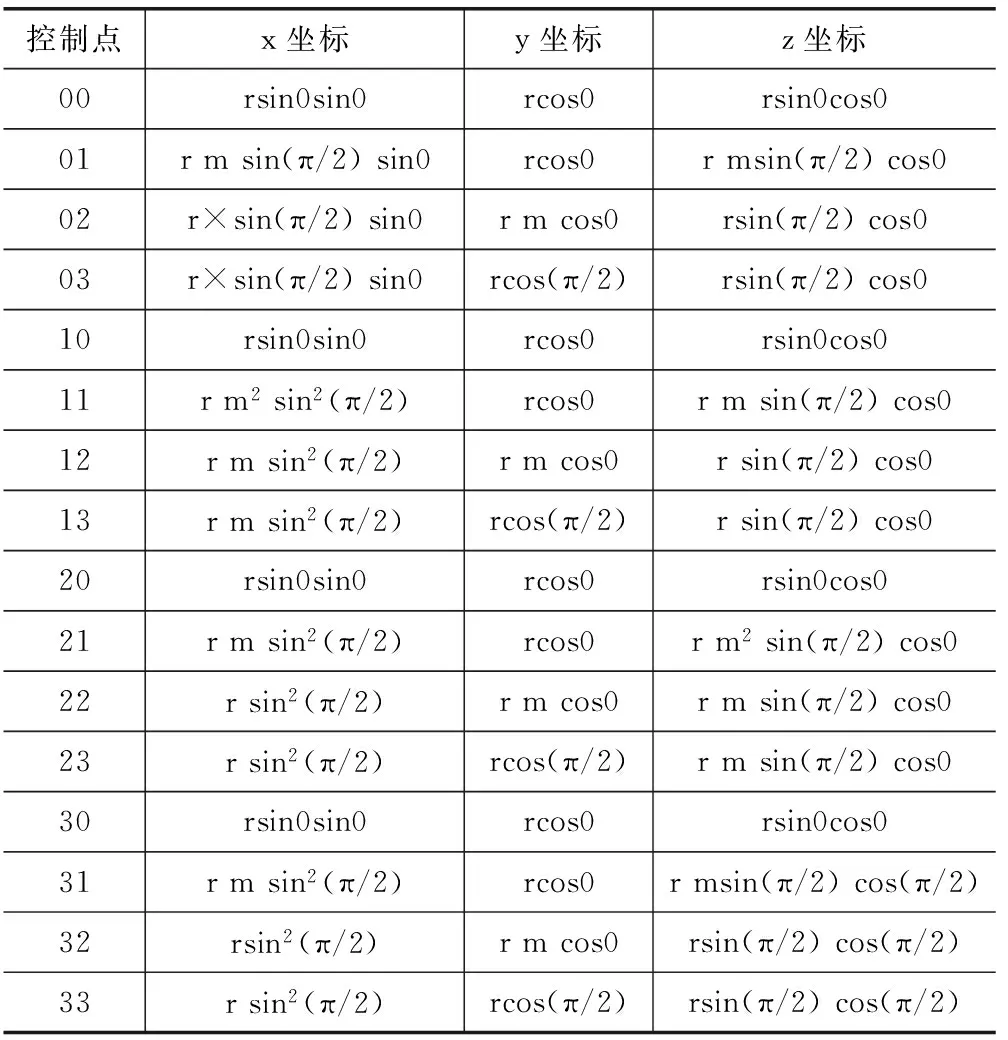
表1 球体第一卦限双三次Bezier曲面控制点数据

3.2 绘制球体网格模型

三次Bezier曲面的参数多项式为：

(u，v)∈[0，1]×[0，1]()

将Bezier曲面方程改写成矩阵形式为：

球体曲面网格模型由8张双三次Bezier曲面片组成，使用表1节给出的控制点数据，对称求出其他卦限曲面片控制点坐标，当参数u和v在区间[0，1]内，以u+=0.1和v+=0.1遍历时，生成球的双三次Bezier曲面网格模型，以VisualC++为平台绘制的球体曲面网格模型和带控制多边形的网格模型如图7所示。

图7 球体双三次Bezier曲面网格模型

3.3 绘制其他曲面体网格模型

椭球曲面模型的控制点的计算，和球体曲面模型控制点计算方法类似，将椭球按卦限分为8个部分，每个卦限为一张双三次Bezier曲面片，用球坐标表示出第一卦限曲面片四个角点(位于椭球上的控制点)的坐标值，曲面片的其他12个控制点(位于椭球之外)依次使用椭球的魔术常数进行计算，并用对称的方法获得其他卦限的曲面片控制点坐标。以VisualC++为平台绘制的椭球曲面网格模型和带控制多边形的网格模型如图8为所示。

图8 椭球双三次Bezier曲面网格模型

Bezier曲线还可以通过调整控制点参数模拟更多的形状。事实上鸡蛋的形状是多种多样的，利用传统的函数绘制的鸡蛋固定长半轴参数a和短半轴参数b后，其形状是确定的，利用Bezier曲面却可以模拟多种鸡蛋形状。如图9所示，鸡蛋右侧边缘由两段三次Bezier曲线组成，上段为1/4椭圆弧，下端为1/4圆弧，水平截面边缘则有4段三次Bezier圆弧构成，调节控制点参数可产生其他形状的蛋形。当调节球体“南北极”控制点参数可生成桃形、苹果形等模型。以VisualC++为平台绘制的鸡蛋和苹果曲面网格模型和带控制多边形的网格模型如图9、图10所示。

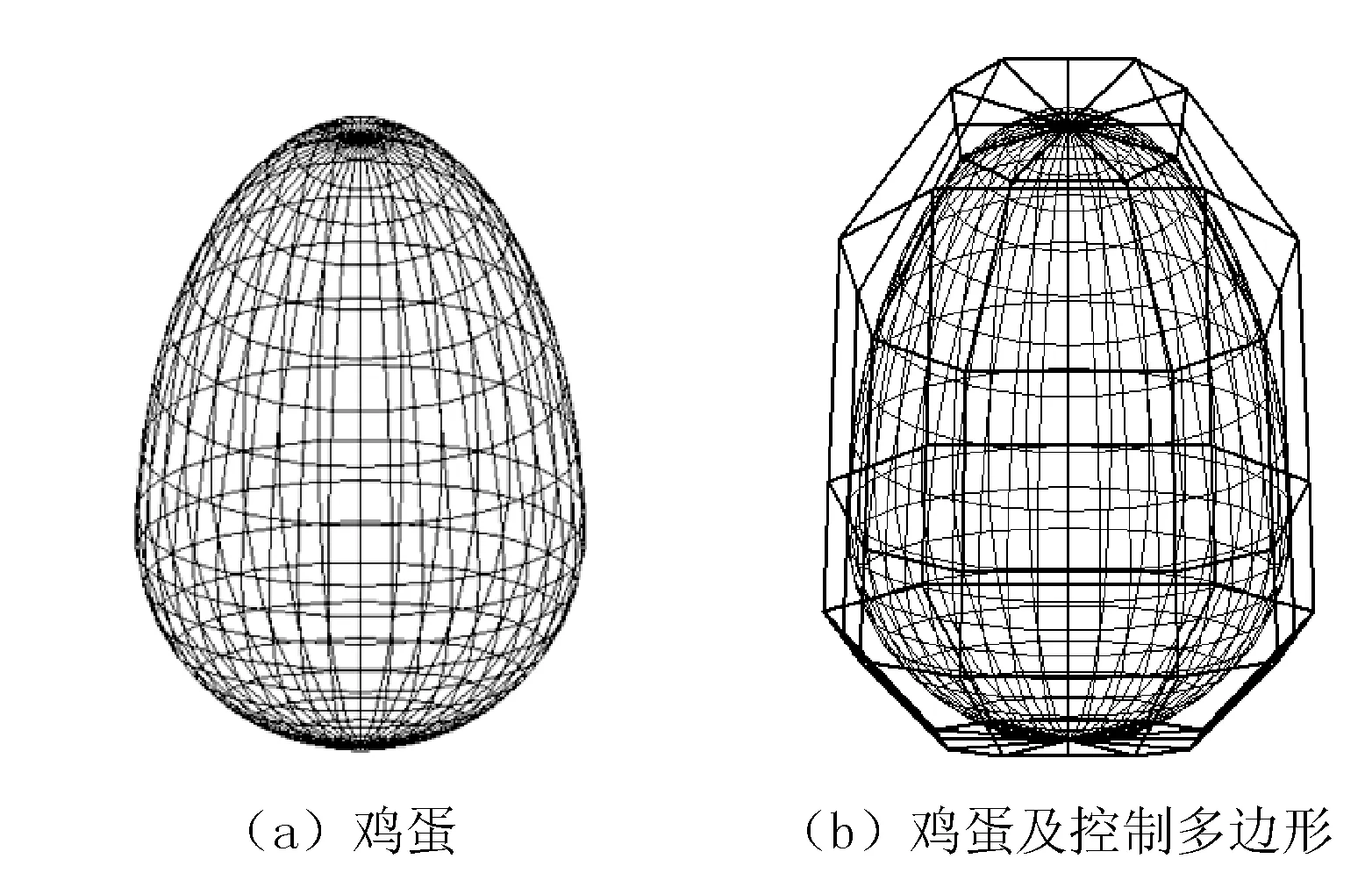
图9 鸡蛋双三次Bezier曲面网格模型

图10 苹果双三次Bezier曲面网格模型

4 结 语

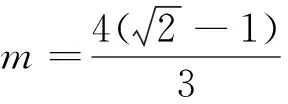
[1] 张博,周丽韫,李兴霞.中点生成椭圆的整数型算法[J].工程图学学报,2011,32(1):1-4.

[2] 牛玉静,唐棣.双步圆的反走样生成算法[J].计算机工程与应用,2010,46(23):175-177,248.

[3] 牛连强,冯海文,吴澎.利用残差控制的快速圆弧生成与反走样算法[J].计算机辅助设计与图形学学报,2011,23(2):232-239.

[4] 郭凤华.几何造型中参数化与拟合技术的研究[D].济南:山东大学,2007.

[5] 杭后俊,李汪根.有理三次Bezier曲线表示圆弧的一种实用方法[J].计算机工程与应用,2012,48(6):185-189.

[6] 储理才,曾晓明.圆弧的四次Bezier曲线逼近研究[C]//第四届全国几何设计与计算学术会议论文集,2009:69-74.

[7] 尤伟,达飞鹏,盖绍彦.逆向工程中求取特征曲线的算法研究[C]//第十二届全国图象图形学学术会议论文集,2005:437-441.

[8] Crow F.The origins of the teapot[J].IEEE Computer Graphics and Applications,1987,7(1):8-19.

[9] 张永锋,蒋大为,何磊,等.基于De Casteljau算法的Poisson细分曲线[J].科学技术与工程,2007,7(10):2263-2267.

APPLICATION OF SPHERICAL MODELING BASED ON BICUBIC BEZIER SURFACE

Kong Lingde Kang Feng’e

(TaiyuanInstituteofTechnology,Taiyuan030008,Shanxi,China)

The geometrical elements of traditional sphere modeling are generated by non-parametric mathematical equation, and the modeling process is complicated and difficult to be deformed to generate other models. Aiming at these problems, this paper proposes a spherical modeling method based on bicubic Bezier surface. Using the De Casteljau subdivision algorithm, the control points of the bicubic Bezier surface of circle and ellipse are solved, the magic constants of the Bezier surface control points are obtained, and the control point coordinates of the bicubic Bezier surface are given. It realizes the drawing of three-dimensional sphere and ellipsoidal grid model based on bicubic Bezier surface. By adjusting the parameters of the control points, a surface grid mode, which is similar to the egg body and the apple body, is generated. The experimental results show that the magic constants provide a new technical support for calculating the control points of the rotating body model, and the Bezier method has a strong design flexibility and practicability for three-dimensional modeling.

Computer application Bicubic Bezier surface De Casteljau subdivision algorithm Control point

2016-04-06。山西省高等学校重点教改基金项目(J2011108)。孔令德，教授，主研领域：图形图像处理。康凤娥，高级实验师。

TP391.7

A

10.3969/j.issn.1000-386x.2017.05.015