层次化聚类在分布式计算环境中的剪枝策略

丁晓阳 罗 阳 王建新

(北京林业大学信息学院 北京 100083)

层次化聚类在分布式计算环境中的剪枝策略

丁晓阳 罗 阳 王建新

(北京林业大学信息学院 北京 100083)

基于树结构中结点覆盖关系的一类层次化聚类算法可以对海量数据生成有意义的摘要。然而，该算法已被证明是NP-完全问题，求解其精确解需要庞大的计算量。虽然它在单机计算环境中存在有效的剪枝方法，但在分布式计算环境中这种剪枝算法并不可行。相应地提出了该层次聚类算法在分布式环境中的剪枝新策略，通过绑定结点与其覆盖的基本事件构成的有序数组，使穷举查询转换为有序数组的求交集运算，并能够在合并过程中执行大量剪枝，从而在有限的额外空间消耗的基础上显著减少计算时间。在2组公开基准数据集上进行了测试，结果表明，相比朴素的分布式计算策略，新的层次化聚类算法在时间效率上平均有30～40倍左右的提升。

层次化聚类算法 分布式计算环境 剪枝操作

0 引 言

聚类分析指在大型数据集中发现积聚现象并加以定量化描述[1]，也就是将一个由大量抽象对象组成的集合分组，并得到由类似的对象组成的多个子集。在近几十年中，随着数据规模的迅猛增长，单纯靠人工很难在海量数据中发现规律与有用的信息，因此，聚类的重要性及其与其他方向研究的交叉特性也越来越受到人们的关注[2]。

传统聚类算法大致可分为层次聚类算法、划分聚类算法、基于密度的聚类算法和基于网格聚类算法等[1-3]。其中，层次聚类算法也可称作树聚类算法[4]，其将数据对象视作若干棵事件树。

层次聚类的方式一般分为凝聚的层次聚类与分裂的层次聚类[1, 3,5]。而本文中的层次聚类—基于树结构中结点覆盖关系的一类层次化聚类算法，既非凝聚也非分裂，而是找出能够覆盖一定数目以上的基本事件且最“紧致”的(也就是最具体的)抽象事件，称之为最小覆盖事件[6-7]。这种层次聚类可以对海量数据生成有意义的摘要[6]。

接下来用实际的问题描述基于树结构中结点覆盖关系的层次聚类，在大量女性化妆品单次消费数据中寻找最常见的某些年龄段的女性单次消费某些金额的频率，便可构建如图1所示的两棵事件树。聚类所处理的数据集是由事件树的叶子结点所构成的大量基本事件。某个女性的年龄与她某次消费的金额所构成的事件，如(“34”,“200”)，即一个基本事件。

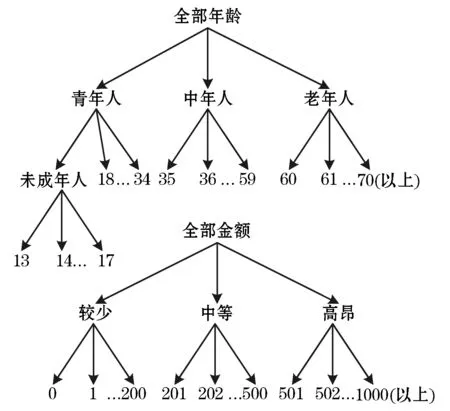
图1 女性年龄(岁)与化妆品消费(元)事件树结构示例

抽象事件是由事件森林(多棵事件树)中的任意结点向量所构成的事件，因此，也可以认为基本事件是一类特殊的抽象事件。两个抽象事件之间距离的判断依据是两个事件对应的分量(结点)间的距离，而同一棵树中两个结点间的距离为结点间有向弧的条数。图1的上图中结点“13”到结点“全部年龄”间的距离为3。但由于结点“未成年人”与结点“34”之间没有祖先-后代关系，因此这两个结点间的距离无定义[6]。

定义1 抽象事件之间的距离定义为其对应分量距离的平均值[4]。若事件森林中共有n棵事件树，di为事件a的第i个分量与事件b的第i个分量之间的距离，则事件a与事件b之间的距离为：

(1)

在图1中，抽象事件(“18”,“中等”)到抽象事件(“18”, “201”)的距离[7]为：

(d(“18”,“18”) +d(“中等”,“201”) )/2=

(0+1)/2 = 0.5

且由于抽象事件(“18”,“201”)中每一个分量均为事件(“18”,“中等”)相应分量本身或其子孙，因此(“18”,“中等”)覆盖(“18”,“201”)。

定义2 若某个抽象事件a覆盖了m个基本事件，d(a,bi)为抽象事件a到其覆盖的第i个基本事件bi之间的距离，则该抽象事件距离其覆盖的所有基本事件的平均距离为：

(2)

所以最小覆盖事件本身也是一个抽象事件，它不仅能覆盖不少于指定阈值数的基本事件，且距其覆盖的所有基本事件的平均距离均值最小(也就是这个抽象事件需要最具体化)。

根据图1描述的情形，若有3个基本事件(“13”,“202”)、(“16”, “215”)与(“60”,“501”)，阈值设置为2，则最小覆盖事件应为(“未成年人”,“中等”)。因为该事件能够覆盖(“13”,“202”)与(“16”,“215”)，且距这2个基本事件的平均距离为1；而其他符合阈值条件的抽象事件距其覆盖的基本事件的平均距离均大于1。例如，(“全部年龄”,“全部金额”)能够覆盖全部基本事件，但其距离所有能覆盖的基本事件的平均距离为2.33，大于1。换句话说，抽象事件(“全部年龄”,“全部金额”)不如(“未成年人”,“中等”)能够更加具体地代表给出的3个基本事件[8]。也就是说，抽象事件(“未成年人”,“中等”)是基本事件的、满足阈值条件的、最有意义的摘要。

可以看出，基于树结构中结点覆盖关系的层次聚类算法的主要思想是在全部抽象事件中找出一个符合要求的抽象事件。在阈值确定的情况下，聚类的结果不仅是唯一的，也是精确的。

基于树结构中结点覆盖关系的层次聚类算法所应用的领域相当广泛。例如，用于应对网络攻击的入侵检测系统(IDS)[9]每天会接收到大量的警报[8]，其中高达99%为由良性事件所触发的误报，导致真阳性事件难以被发现[10]。如此大量的误报会给操作者和决策者带来很大负担，为此,可采用如图2所示的树形结构进行层次聚类，帮助操作者理解和判断[7]。

图2 入侵检测系统ip地址与端口分类树结构示例

基于树结构中结点覆盖关系的层次聚类已被证明为一种NP-完全问题[6, 11]，即随着树结构数量的增加无法在多项式时间内求得解的问题[12]。这类问题无法通过计算求得正确解，但可验证某个解是否正确[13]。换句话说，每个抽象事件均可能是最小覆盖事件，但不存在直接找出最小覆盖事件的多项式时间算法，在理论上每个抽象事件都要进行判断。Julisch[10]给出了如下的近似算法[14]。

输入：一组基本事件；阈值T；一组事件树

输出： 一个抽象事件

选择任意由叶子结点组合构成的抽象事件A

当 (A覆盖的基本事件数小于T) {

选择抽象事件A的任意一个结点a；

用a的父结点b替换a；

把A更新为包含b的更加抽象的事件。

}

返回抽象事件A

全部抽象事件的数量为每个事件树结点数的笛卡尔积。表1为由图3中事件树所组成的所有抽象事件。

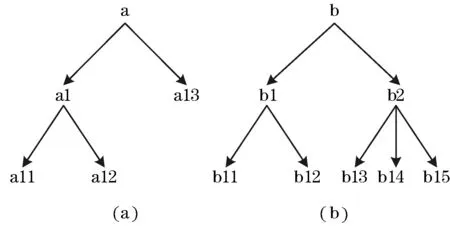
图3 简化事件树示例

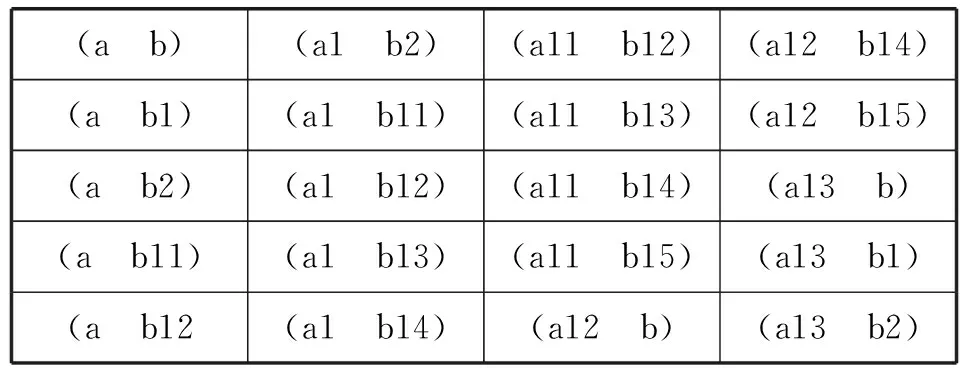
(a b)(a1 b2)(a11 b12)(a12 b14)(a b1)(a1 b11)(a11 b13)(a12 b15)(a b2)(a1 b12)(a11 b14)(a13 b)(a b11)(a1 b13)(a11 b15)(a13 b1)(a b12(a1 b14)(a12 b)(a13 b2)

续表1

表1中所有抽象事件是图3中(a)树的所有结点集和(b)树的所有结点集的笛卡尔乘积，因此有5×8=40个抽象事件。

随着事件树个数的增多，抽象事件数将以指数形式增长，计算量也将愈加庞大。算法的时间复杂度高也是层次聚类普遍具有的缺点[1]。为应对该问题，需要分布式计算的手段，使聚类任务在多个计算节点上并行处理。目前流行的聚类分析的策略是将聚类算法与常用于处理大数据的分布式计算平台相结合，设计出高效的算法[15-16]。对于一个需要十分巨大的计算能力才能解决的问题，分布式计算能将该问题分成许多小的部分，再将这些部分分配给多台计算机进行并行运算[17]。

集群是分布式计算环境中的常用结构之一。在该结构中，各个计算机之间通信较少，运算基本上独立进行。为了统计某个抽象事件覆盖的基本事件数，并不是将基本事件数据存储到集群，而需将所有抽象事件分布到集群中，通过并行计算找出最小覆盖事件，这样可以显著减少计算时间，一定程度上解决这种NP-完全问题中的适中的输入规模问题。事实上，基于结点覆盖关系的层次化聚类分析中所用的树结构的数量一般在3至10棵，是可以通过分布式计算获得其精确最优解的。分布式计算方法MapReduce模型[18-19]是比较适合的处理方式之一，其核心思想为将执行的问题拆解成映射(Map)和规约(Reduce)操作，即先通过Map程序将数据分割，分配给大量计算机处理，再通过Reduce程序将结果汇总，输出结果[18-19]。

然而在以往的研究中，前文所述层次聚类并不适合在分布式集群中解决。由于所有的抽象事件均由事件树结点构成，因此抽象事件间有一定的耦合关系，即一个抽象事件需要根据与其关联的其他抽象事件判断其是否覆盖某个或某些基本事件。若在单机环境中进行层次聚类，程序可以跳过这些被推断为不符合条件的抽象事件，从而大大减少运算时间。这种操作称为“剪枝”。但要处理更大规模的树结构集合，则单机处理方案因计算能力有限而不可行。若在集群上进行该层次聚类操作，则抽象事件会作为相互独立的个体分布到集群中，导致上述剪枝操作无法实施。而对所有的抽象事件进行所有基本事件的覆盖判断会大大增加计算时间耗费。

针对上述问题，本文提出了一种新的层次聚类机制—基于有序数组的分布式层次聚类算法，称为DHCSA (Distributed Hierarchical Clustering based on Sorted Arrays)，其中使用了一种剪枝新策略，既满足分布式计算条件，也就是将抽象事件视作独立个体，又可以进行剪枝，从而大大减少聚类消耗的时间。该算法能借助集群对大数据和密集计算的处理能力，解决这种NP-完全问题中常见的输入规模情形。

1 单机层次聚类剪枝和朴素分布式方案概述

聚类算法在单机上运行时，会有诸如单位时间内处理量小、对大量数据处理的时间会很长等问题。但较小规模的层次聚类算法能在单机环境下高效运行，得益于其剪枝策略，即部分抽象事件可以直接略过不进行处理。

1.1 输入数据预处理

如表2所示，在聚类前对基本事件进行分类统计，得到每个基本事件的统计信息(即个数)。

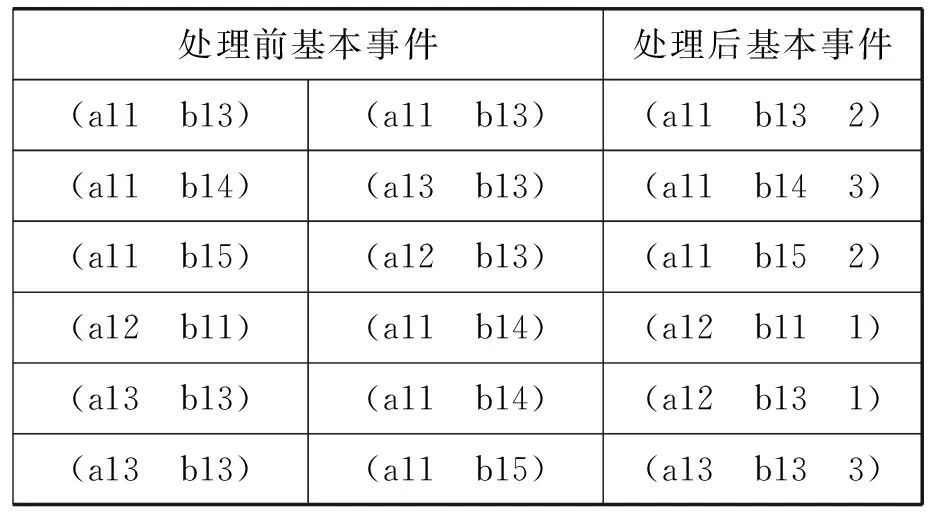
表2 输入数据预处理示例

在表2中，每种基本事件在预处理之前都是结点向量的形式；在预处理之后，相同的基本事件被合并，重复出现的次数增添为向量的最后一个分量。

1.2 单机层次聚类剪枝原理概述

在事件森林中，按照如图4所示的路径顺序遍历每棵事件树的结点，从而遍历所有抽象事件，统计每个抽象事件覆盖的基本事件数。统计的方法如下[20]：

遍历过程中的一个基本的操作是判断抽象事件与每个基本事件的覆盖关系。为此，首先判断抽象事件的第一个分量是否覆盖基本事件的第一个分量，若是，则依次判断之后的分量；否则不能覆盖，直接跳到下一个基本事件。若该抽象事件的所有分量均覆盖该基本事件的相应分量，则该抽象事件覆盖该基本事件，将该基本事件的重复次数加到该抽象事件的覆盖事件数中。

若该抽象事件的覆盖事件数超过指定阈值，则计算它到其覆盖的所有基本事件的平均距离。若小于之前找出的最小覆盖事件的平均距离，则将该抽象事件取代已知的最小覆盖事件，成为当前的最小覆盖事件。

在前序遍历抽象事件中，当某个抽象事件覆盖的基本事件数小于阈值时，便可以进行剪枝，即跳过由该抽象事件所覆盖的所有其他抽象事件。以图3为例，若抽象事件(a1, b1)覆盖的基本事件数小于阈值，则可跳过由 (a1, b1)所覆盖的其他抽象事件，如(a1, b11)和(a11, b1)等，并继续由抽象事件(a1, b2)开始判断。

图4 前序遍历树示意图

1.3 朴素分布式层次聚类算法原理概述

朴素分布式层次聚类算法与单机层次聚类算法的基本事件数据预处理的方式相同，也是对基本事件进行分类统计。

而对于抽象事件的遍历并非基于事件树的遍历，而是将所有的抽象事件生成一个新的数据集，并分布到集群的各个计算节点中去。新的数据集如表1所示，它是由图3所示树结构形成的所有抽象事件集。

与单机层次聚类算法相似，朴素分布式层次聚类算法需要遍历抽象事件集，判断每个抽象事件覆盖的基本事件数。若覆盖数超过阈值，则计算平均距离，最终找出最小覆盖事件。但是，集群环境中的每个计算单元只考虑本单元所分配的抽象事件是满足阈值条件，而且给管理单元汇报其中距离最小的抽象事件；管理单元在所有计算单元汇报的抽象事件中再选取距离最小者，作为最终结果。

可以看出，与单机环境中的层次聚类算法相比，朴素的分布式层次聚类算法中各个抽象事件之间是独立判断的，没有依赖关系，没有信息共享，因此不能进行剪枝，从而致使效率低下。而在单机环境下，一个抽象事件不满足阈值条件，可以推理出若干个抽象事件也不满足阈值条件，从而形成有效的剪枝。因此，需要进一步挖掘在分布式环境中的可行的剪枝方式。

2 DHCSA算法原理概述

为了在分布式环境下运行，DHCSA算法也需要对所有抽象事件进行判断，而判断过程中使用了一种新的剪枝方式。

2.1 输入数据预处理

DHCSA算法的数据预处理是在单机版本算法的数据预处理的基础上，为每种基本事件添加一个编号，如表3所示。

表3 DHCSA算法输入数据预处理示例

2.2 事件树预处理

分别遍历每棵事件树，并给每个结点绑定一个有序数组，其内容为所有包含其覆盖结点的基本事件编号，如图5所示。例如，a1绑定的数组为所有包含a11与a12的基本事件编号。由于根结点必包含所有基本事件编号，因此可不进行处理。

图5 树结点挂接的有序数组

以下为绑定数组的方法和步骤：

(1) 在找出某结点所要绑定的所有基本事件编号时，可将所有基本事件按照该结点所在树的叶子结点的顺序进行排列，借助该序列可提高绑定数组的效率，如表4所示为分别根据a树与b树的叶子结点顺序排列的基本事件。

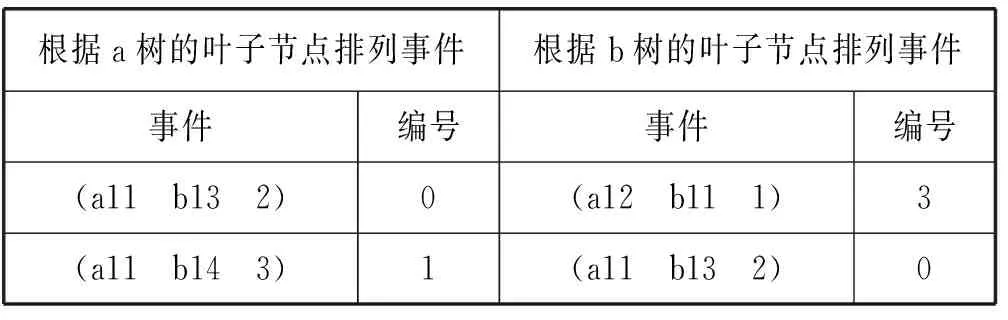
表4 事件树预处理示例(根据树结构(a与b)排列事件)

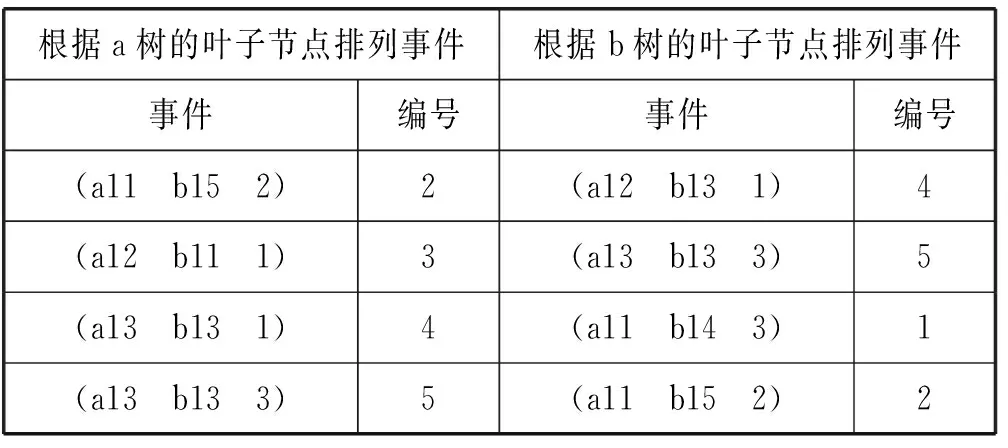
续表4

(2) 为每个结点绑定数组。如表5所示，若处理的是叶子结点，以b13为例，直接将包含b13的事件编号组成数组赋予b13，共3种基本事件。

表5 叶子结点的数组示例(结点b13的数组)

(3) 若处理的是非叶子结点，则如表6所示，在根据该树排序的基本事件集中找出该结点的左叶子结点与右叶子结点。以b2为例，找出b13与b15；将包含b13的事件、包含b15的事件及两者之间的事件编号共同组成有序数组赋予b2，共3+1+1=5种基本事件。

表6 非叶子结点的数组示例(结点b2的数组)

2.3 找出最小覆盖事件

遍历所有的抽象事件，根据每个结点所绑定的数组判断其是否为覆盖某个或某些基本事件。某个结点所覆盖的基本事件的数量可以通过它所绑定的数组计算取得：即把数组的每个元素(即某种基本事件的序号)对应的基本事件重复次数相加。例如在表6中，结点b2对应的数组是[0, 1, 2, 4, 5]，那么b2对应的基本事件的数量是2+3+2+1+3=11。

显然，将抽象事件中所有结点对应的数组取交集的结果即为该抽象事件所覆盖的所有基本事件。如果所覆盖基本事件数小于指定的阈值，则该抽象事件可跳过。因此，在这里可以进行另一种剪枝。

(1) 将当前抽象事件结点向量(结点个数为n)对应的n个数组按照数组长度由小到大进行排序：如抽象事件(a1, b11)对应的两个数组分别为[0, 1, 2, 3, 4]和[1]，则排列后为[1]和[0, 1, 2, 3, 4]，也就是优先对b11对应的数组[1]进行处理。

(2) 判断第一个数组中基本事件的个数和是否小于阈值。若是，则说明该抽象事件所覆盖的基本事件数必定小于阈值，因此直接跳过并处理下一个抽象事件，这一步即新的剪枝；否则(第一个数组中事件的个数符合阈值条件)，则将其与之后的数组依次取交集，且每次均判断其结果所包含的基本事件数与阈值的大小关系；一旦小于阈值，则判断终止，并跳转到下一个抽象事件。

(3) 若最终所有数组的交集所包含的基本事件数仍大于阈值，则计算该抽象事件到所有其覆盖的基本事件的平均距离。整个过程中出现的平均距离最小的抽象事件即为最小覆盖事件。

2.4 算法特点

DHCSA算法中所有抽象事件之间均为独立的，因此可以运行在分布式集群上；并且在计算过程中执行大量的剪枝操作，能够显著减少计算时间。这一过程中的一个常用操作是求两个有序数组的交集。众所周知，如果两个或多个数组是无序的，则求交集运算的时间复杂度是平方级别的；但如果数组是有序的，则这个操作的时间复杂度是线性的，因此运算效率很高。这也是DHCSA算法高效性的主要因素之一。如表7所示为新旧两种剪枝方法的特点比较。

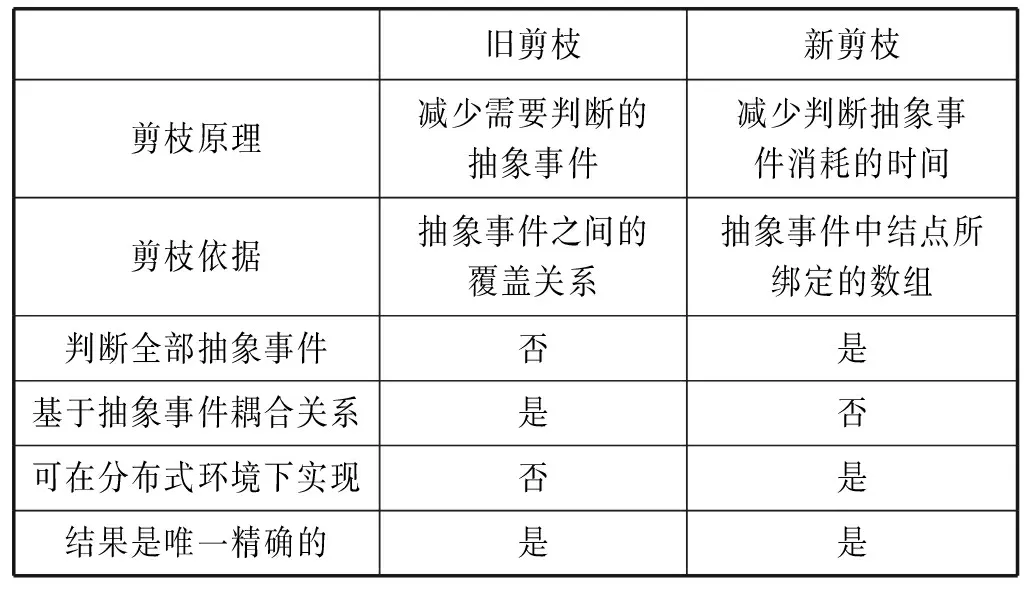
表7 新旧两种剪枝策略特点对比

3 实验方法与结果分析

由于并不存在其他能够在分布式环境下实现的剪枝策略，因此在本节中，将在分布式环境下用基准数据集对朴素分布式层次聚类算法与DHCSA算法的效率进行比较，验证DHCSA算法的有高效性。

3.1 实验环境和数据集

集群由2台普通PC组成，其中一台作为主节点(master)，另一台作为从节点(slave)；在Linux操作系统Ubuntu中全部采用Java环境，JDK版本是：JDK1.6.0-39；实验与编译环境：Eclipse SDK 3.5.2；Hadoop[21,22]平台：Hadoop 0.20.2。

本文选取了UCI数据集[23]中的2个数据集对DHCSA算法与朴素分布式层次聚类算法的效率进行比较，所列信息包括数据集名称、基本事件数、事件树数量和抽象事件数等内容。数据集的具体信息如表8所示。

表8 实验所使用的UCI数据集

3.2 算法效率比较试验

实验内容是在相同的环境和平台上分别运行DHCSA算法和与朴素分布式层次聚类算法的效率，两种算法所得出的结果都是完全一致的。实验结果如表9所示(其中，T1为朴素分布式层次聚类算法所消耗时间；T2为DHCSA算法所消耗时间)：

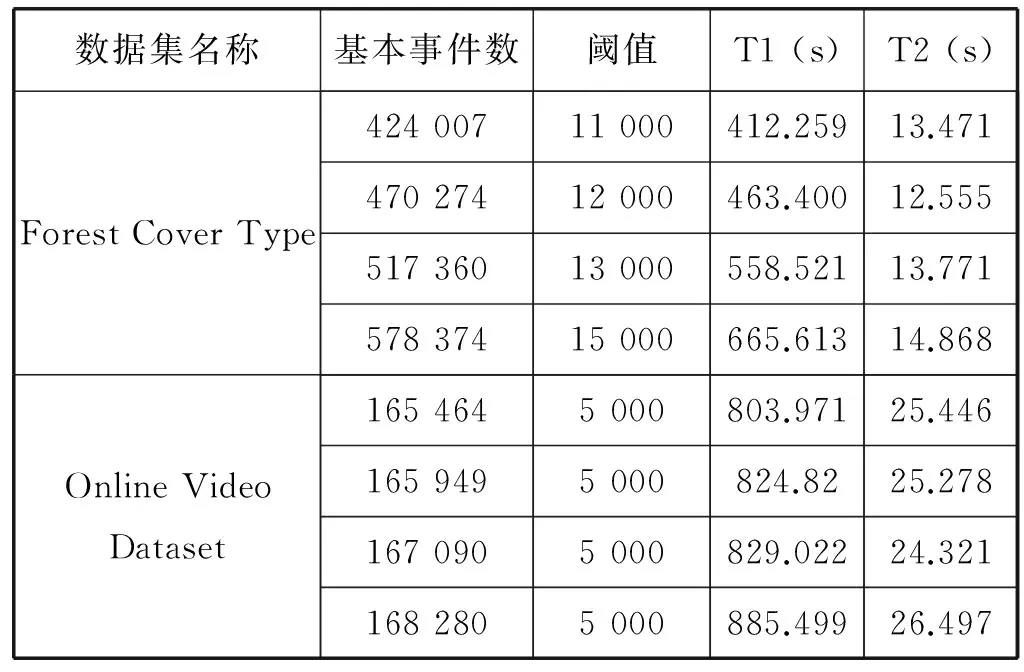
表9 两种算法找出最小覆盖事件所需时间对比

图6是朴素的分布式聚类算法和新提出的聚类算法DHCSA处理相同的数据集所需时间的对比图。图中横轴是经过树结构分割处理后，数据集所产生的基本事件数量；纵轴是聚类所需时间。

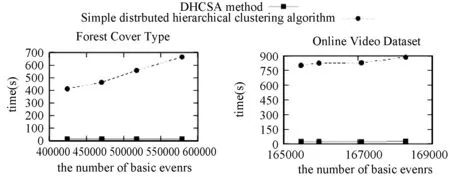
图6 两种分布式聚类算法耗时对比图

由图6可看出，相比朴素的分布式计算策略，DHCSA算法在时间效率上至少有30倍的提升，有些甚至超过40倍；且随着基本事件数的增多，DHCSA算法的效率提升更明显。

4 结 语

本文提出一种新型层次聚类算法DHCSA，针对单机版剪枝操作无法在集群上实现、朴素分布式层次聚类算法效率低等问题，采用了一种不涉及抽象事件之间耦合关系的新剪枝策略，使层次化聚类算法能够高效地在分布式集群上运行。实验结果表明，对于数据量的不同大小和事件的不同复杂程度，DHCSA算法的运算效率均远高于朴素分布式层次聚类算法，并且数据量越大，DHCSA算法的高效率特性便越显著。

[1] 周涛, 陆惠玲. 数据挖掘中聚类算法研究进展[J]. 计算机工程与应用, 2012,48(12):100-111.

[2] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008,19(1): 48-61.

[3] 覃艳, 王洪, 周全华. 数据挖掘中聚类算法的研究[J]. 网络安全技术与应用, 2014 (1): 65-66.

[4] Marquesdesa J P. 模式识别——原理, 方法及应用[M]. 吴逸飞，译. 清华大学出版社，2002: 51-74.

[5] 韩家炜, Kamber M. 数据挖掘: 概念与技术[M]. 3版. 机械工业出版社，2012:298-300.

[6] Julisch K. Mining alarm clusters to improve alarm handling efficiency [C] //Computer Security Applications Conference. IEEE, 2001: 12-21.

[7] Wang Jianxin, Zhao Geng, Zhang Weidong. A subjective distance for clustering security events [C] //Communications, Circuits and Systems. IEEE, 2005, 1: 74-78.

[8] Julisch K. Dealing with false positives in intrusion detection [C]. In: Recent Advances in Intrusion Detection(RAID 2000), Toulouse, 2000: 113-119.

[9] 隋新, 刘莹. 入侵检测技术的研究[J]. 科技通报, 2014, 30(11): 89-94.

[10] Julisch K. Clustering intrusion detection alarms to support root cause analysis [J]. ACM Transactions on Information and System Security (TISSEC), 2003, 6(4): 443-471.

[11] Julisch K, Dacier M. Mining intrusion detection alarms for actionable knowledge [C] // Proceedings of the 8th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2002: 366-375.

[12] 李昭智. NP-完全问题浅谈[J]. 天津理工大学学报, 1984(1): 27-34.

[13] 杜立智, 符海东, 张鸿, 等. P 与 NP 问题研究[J]. 计算机技术与发展, 2013, 23(1): 37-42.

[14] Wang Jianxin, Wang Hongzhou, Zhao Geng. A GA-based solution to an NP-hard problem of clustering security events [C] //Communications, Circuits and Systems Proceedings. IEEE, 2006, 3: 2093-2097.

[15] 崔建, 李强, 杨龙坡. 基于垂直数据分布的大型稠密数据库快速关联规则挖掘算法[J]. 计算机科学, 2011, 38(4): 216-220.

[16] 郑湃, 崔立真, 王海洋, 等. 云计算环境下面向数据密集型应用的数据布局策略与方法[J]. 计算机学报, 2010, 33(8): 1472-1480.

[17] 葛澎. 分布式计算技术概述[J]. 微电子学与计算机, 2012, 29(5): 201-204.

[18] 李成华, 张新访, 金海, 等. MapReduce: 新型的分布式并行计算编程模型[J]. 计算机工程与科学, 2011, 33(3):129-135.

[19] 刘向东, 刘奎, 胡飞翔, 等. 基于MapReduce的并行聚类算法设计与实现[J]. 计算机应用与软件, 2014,31(11):251-256.

[20] 肖政, 王建新, 侯紫峰, 等. 基于搜索树的告警高效聚类算法和 Bayes 分类器的设计和研究[J]. 计算机科学, 2006, 33(8): 190-194.

[21] 沈利香, 曹国. 分布式计算环境下的入侵检测数据分类研究[J]. 计算机与现代化, 2015 (12): 43-47.

[22] 陆嘉恒. Hadoop实战[M]. 机械工业出版社, 2011:2-10.

[23] Merz C J, Murphy P M. UCI Repository of machine learning datasets [EB/OL]. (1998). http//www.ics.uci. edu/～mlearn/MLRepository.html.

PRUNING STRATEGY OF HIERARCHICAL CLUSTERING IN DISTRIBUTED COMPUTING ENVIRONMENT

Ding Xiaoyang Luo Yang Wang Jianxin

(SchoolofInformation,BeijingForestryUniversity,Beijing100083，China)

A hierarchical clustering algorithm based on the node coverage relation in the tree structure can generate meaningful abstracts for the massive data. However, this algorithm has been proved to be an NP-complete problem, and its exact solution requires a large amount of computation. Although it has an effective pruning method in stand-alone computing environment, this pruning algorithm is not feasible in a distributed computing environment. A new pruning strategy of hierarchical clustering algorithm in distributed environment is proposed. By binding an ordered array of nodes and basic events that they cover, an exhaustive query is converted to an intersection set of ordered arrays, and a large number of pruning can be performed during the merge process. Thereby significantly reducing the computational time on the basis of limited additional space consumption. Tests were performed on two sets of open reference datasets. The results show that the new hierarchical clustering algorithm has 30～40 times improvement in time efficiency compared with the simple distributed computing strategy.

Hierarchical clustering algorithm Distributed computing environment Pruning operation

2016-05-04。丁晓阳，硕士生，主研领域：数据挖掘。罗阳， 硕士生。王建新，教授。

TP3

A

10.3969/j.issn.1000-386x.2017.05.045