一类脉冲反应扩散系统的行波和传播速度

沈林, 周红玲

(黄淮学院数学科学系,河南 驻马店463000)



一类脉冲反应扩散系统的行波和传播速度

沈林, 周红玲*

(黄淮学院数学科学系,河南 驻马店463000)

讨论了开放环境中一类具有固定脉冲时刻的反应扩散系统的传播速度和行波解。在空间分布均匀条件下， 给出了正常数解存在和稳定的条件。得到了脉冲反应扩散系统传播速度的具体表达形式，当满足一定条件时，传播速度大于零，该速度也是系统存在行波解的最小速度。以水流速度为参数对系统进行了数值模拟，结果表明通过控制扩散系数、水流速度、离散和连续时间的死亡率和出生率，可实现生物种群的传播和持久生存。

脉冲反应扩散系统; 传播速度; 行波

现阶段，生物种群的传播和持久生存备受研究者的青睐，大多数研究者在假设生物种群的扩散、出生和死亡连续地依赖于时间和空间的前提下，利用反应扩散方程进行建模，并成功地模拟了部分生物种群在开放环境中的传播和持久生存。但是，大多数鱼类和小型昆虫的繁衍是与季节息息相关的，而且这些生物的繁衍阶段与生长阶段相比是极短的[1-2]，因此, 单纯利用反应扩散方程不能很好地描述生物的繁衍。针对生物种群离散的出生率，Lewis 等[3]建立了如下脉冲反应扩散系统

(1)

其中，d为扩散系数，α<0为种群的死亡率，r反映种群间的竞争，Nn(x)为第n代繁衍前在x点的种群密度，g(Nn)为繁衍后在x点的种群密度，τ为每一代的生长周期，一个周期生物种群只繁衍一次。本文在上面系统中加入水流速度(风速)，并假设g(N)为Beverton-Holt函数[4]，可得到下面脉冲反应扩散系统

(2)

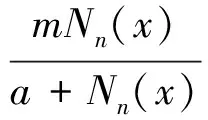
1 开放环境中脉冲ODE系统

计算可得：

定理1

证明

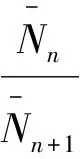
综上可得：

又因为

以此类推，可得

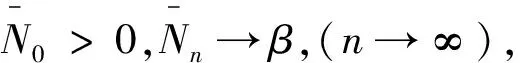
2 开放环境中脉冲PDE系统

脉冲反应扩散系统(2)的线性化系统为

(3)

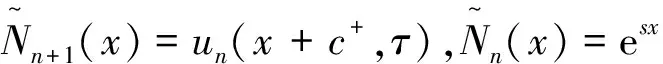
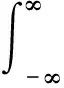
进而可得

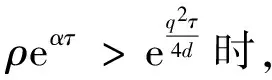
通过验证可知Nn+1(x)=Q[Nn(x)]满足H1 ～ H5 。

H1：当Nn(x)∈[0,β]时，Nn+1(x)=Q[Nn(x)]∈[0,β] 。

所以，Ty{Q[Nn(x)]}=Q{Ty[Nn(x)]} 。

H3：存在区间[0,β]，当u∈[0,β]时，Q(u)>u，且Q(0)=0,Q(β)=β。

H4：由比较原理可知,u≤v时，Q(u)≤Q(v)。

H5：因为g(u)为可微函数，且Qτ在[0,β]是完备的，所以Q在[0,β]也是完备的。

综上，利用Weinberger在文献[5]中的结论，可得到定理2。

3 数值模拟

本节主要研究流水速度对种群传播的影响，各个参数的具体取值见表1。

表1 参数取值

图1 当q=0.5时，行波解的数值模拟Fig.1 A numerical approximation to traveling waves with q=0.5

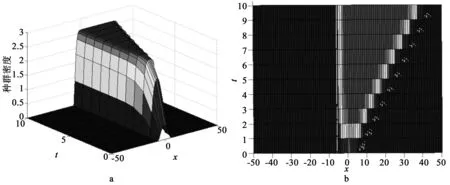
图2 当q=1时，行波解的数值模拟Fig.2 A numerical approximation to traveling waves with q=1

图3 当q=3.3时，行波解的数值模拟Fig.3 A numerical approximation to traveling waves with q=3.3

图4 当q=10时，行波解的数值模拟Fig.4 A numerical approximation to traveling waves with q=10

4 结论

讨论了一类具有脉冲出生与连续死亡的单种群动力学系统，给出了系统传播速度的具体表达形式，借助传播速度得到了该系统行波解[7-11]存在的条件，同时，研究了水流速度对行波解的影响，所得结论对于现实的生态平衡保护是十分有益的。

[1]WECKERLY F W. Matrix population models: construction, analysis and interpretation [J]. Natural Resource Modeling，2001，14(4): 593-595.

[2]VASILYEVA O, LUTSCHER F, LEWIS M. Analysis of spread and persistence for stream insects with winged adult stages[J]. Journal of Mathematical Biology, 2016, 72(4):851-875.

[3] LEWIS M A, LI B. Spreading speed, traveling waves, and minimal domain size in impulsive reaction-diffusion models[J]. Bulletin of Mathematical Biology, 2012, 74(10):2383-2402.

[4] ESKOLA H T M, GERITZ S A H. On the mechanistic derivation of various discrete-time population models [J]. Bulletin of Mathematical Biology, 2007, 69:329-346.

[5]WEINBERGER H F. Long-time behavior of a class of biological models[J]. Siam Journal on Mathematical Analysis, 1982, 13(3):353-396.

[6] MÜLLER K. The colonization cycle of freshwater insects[J]. Oecologia, 1982, 52(2):202-207.

[7] JIN Y, LEWIS M A. Seasonal influence on population spread and persistence in streams: Critical domain size[J]. SIAM Journal on Applied Mathematics. 2011, 71(4):1241-1262.

[8] JIN W, SMITH H, THIEME H R. Persistence and critical domain size for diffusing populations with two sexes and short reproductive season[J]. Journal of Dynamics and Differential Equations. 2016, 28(3):689-705.

[9] LIN Y, WANG Q R. Spreading speed and traveling wave solutions in impulsive reaction-diffusion models[J]. Communications in Nonlinear Science & Numerical Simulation, 2015, 23(1/2/3):185-191.

[10]RAWAL N, SHEN W, ZHANG A. Spreading speeds and traveling waves of nonlocal monostable equations in time and space periodic habitats[J]. Discrete & Continuous Dynamical Systems, 2015, 35(4): 1609-1640.

[11]LIANG X, ZHAO X Q. Spreading speeds and traveling waves for abstract monostable evolution systems[J]. Journal of Functional Analysis, 2010, 259(4):857-903.

Traveling waves and spreading speed to impulsive reaction-diffusion models

SHEN Lin, ZHOU Hong-ling*

(Department of Mathematics, Huanghuai University, Zhumadian 463000，China)

∶In this paper, an impulsive reaction-diffusion model with fixed moments of impulses in an unbounded domain was proposed, and the existence of spreading speed and traveling wave solutions for the model were established. First, the existence and the stability of the positive constant solutions were proved in ODE system. Second, the explicit formula of spreading speed to impulsive reaction-diffusion model was given. When certain conditions were satisfied, the spreading speed was greater than zero, which was the minimum speed of the traveling wave solutions. Finally, the numerical simulation of the system was carried out with the velocity of the water flow. The results reveal that the spread and persistence dynamics of the biotic population can be realized through the control of diffusion coefficient, flow velocity, mortality and birthrate corresponding to discrete time and continuous time respectively.

∶impulsive reaction-diffusion models; spreading speed; traveling waves

2017-08-03

国家自然科学基金(11371164)；国家自然科学基金委员会河南省人民政府人才培养联合基金(U1304104)

沈林(1983—), 男, 讲师, 研究方向为偏微分方程及其可视化。

*通信作者，周红玲。E-mail：8210s@163.com

O175.26

A

1002-4026(2017)03-0088-06