带有大初始值和真空的Navier-Stokes-Maxwell系统的整体解
孔春香
(延安大学数学与计算机科学学院, 陕西 延安 716000)
带有大初始值和真空的Navier-Stokes-Maxwell系统的整体解
孔春香
(延安大学数学与计算机科学学院, 陕西 延安 716000)
考虑了Navier-Stokes-Maxwell系统的初边值问题,借助经典的能量方法和一些先验估计,获得了系统的整体球对称古典解。在这里允许真空和大初始值存在。
Navier-Stokes-Maxwell系统;整体古典解;真空;先验估计
1 引言
在这篇文章中,我们考察(0,∞)×Ω上Navier-Stokes-Maxwell系统:
(1)
其中,ρ,u,E,H,P分别表示流体的密度、速度、电场、磁场和压力。正常数ν和ρb表示粘性系数和背景离子密度。Ω={x∈R3:a<|x| (2) (3) u(x,t)→0,|x|→a,b,t≥0,E(x,t)→0,|x|→a,t≥0。 (4) (5) 通过(5)式直接计算得 divu=Δu,u×H=0,×H=0,×E=0。 (6) 方程(1)变为 (7) 初始条件(3)和边界条件(4)变为: (8) u(r,t)→0,r→a,b,t≥0,E(r,t)→0,r→a,t≥0。 (9) 由方程(7),(8)进行计算得 (10) 因此(7)式又可以写为 (11) 初始条件(8)和边界条件(9)变为: (12) (13) 在具有初始真空和大初值条件下,Fan等[1]考虑了系统(1)的整体球对称古典解的存在性和唯一性。Hong等[2]研究了具有洛伦兹力的可压缩的Navier-Stokes-Maxwell 系统的初边值问题,而且还获得了球对称古典解的存在性和唯一性。对于Cauchy问题,冯跃红等[3]借助经典的能量方法和对称技巧研究了三维全空间中Navier-Stokes-Maxwell 方程组解的渐近行为。Duan等[4]建立了三维可压缩的系统(1)的整体解的存在性和大时间性质。 当电场和磁场不存在时,系统(1)就变成了Navier-Stokes方程组,有关Navier-Stokes方程组解的整体存在性和唯一性已有许多结果[5-7]。当磁场不存在时,系统(1)就变成了Navier-Stokes-Poisson方程组,Li等[8]获得了整体解的收敛率估计。在压力满足p(ρ)=aρlogdρ下,Zhang等[9]建立了Navier-Stokes-Poisson方程组解的整体存在性。 νΔu-P(ρ0)=ρ0g, (14) 在定理的假设下,下面引理都是成立的。 引理2.1 在定理的假设下,下列估计式成立: utt∈L2(0,T;L2(a,b)), Et∈C(0,T;H2(a,b)), E∈C([0,T];H3(a,b))。 证明 见参考文献[2]。 引理2.2 对∀T>0,下列估计式成立: 证明 见参考文献[5], m=2。 证明 由方程(11)中第2式关于r求两次导数得 利用引理2.1和2.2得 引理2.4 对∀T>0,下列估计式成立: 证明: 对(11)中第3式关于t求导,两边乘以Ett,利用Young不等式及引理2.1得 引理2.5 在定理的假设下,对∀T>0,下列估计式成立: 证明 将(11)第2式变形得 (15) 对(15)式关于t求导得 (16) (16)式关于t求导,结果乘以r2ρ2utt,在[a,b]上积分,利用2.1, Cauchy不等式得 从而有 上式在[0,t]上积分,利用引理2.1、2.2和2.4得 由(16)式,相容性条件(14)得 从而有 (17) (16)式关于r求导得 (18) 由(17)、(18)式,引理2.1、2.2及Sobolev不等式得 引理2.6 对∀T>0,下列估计式成立: 证明 见参考文献[5],m=2。 引理2.7 对∀T>0,下列估计式成立: 证明 (16)式关于t求导,结果乘以r2ρ4uttt,分部积分得 利用引理2.1、2.2、2.4、2.5、2.6和Cauchy不等式得引理2.7。 证明 对(11)中第4式关于r求三次导数,得 利用引理2.1、2.2有 对(11)中第3式分别关于r,t求导,利用引理2.1得 对(11)中第3式分别关于r求三次导数,利用引理2.1,2.2得 联立引理2.1~2.8我们完成了定理1的证明。 [1]FAN J S, LI F C, NAKAMURA G. Uniform well-posedness and singular limits of the isentropic Navier-Stokes-Maxwell system in a bounded domain[J]. Zeitschrift für angewandte Mathematik und Physik, 2015, 66(4): 1581-1593. [2] HONG G Y, HOU X F, PENG H Y ,et al. Global spherically symmetric classical solution to the Navier-Stokes-Maxwell system with large initial data and vacuum[J]. Sci China Math,2014, 57(12):2463-2484. [3]冯跃红,王术,双极完全可压缩Navier-Stokes-Maxwell 方程组光滑解的渐近行为[J].北京工业大学学报,2014.40(5):788-795. [4]DUAN R J, Green′s function and large time behavior of the Navier-Stokes-Maxwell system[J].Anal Appl,2012, 10(2):133-197. [5] DING S J, YAO L ZHU C J. Global spherically symmetric classical solution to compressible Navier-Stokes equations with large initial data and vacuum[J].J Math Anal,2012,44(2)1257-1278. [6]WEN H Y, ZHU C J. Global classical large solutions to Navier-Stokes equations for viscous compressible and heat-conducting fluids with vacuum[J]. J Math Anal, 2013, 45(2):431-468. [7] GUO Z H, LI H L, XIN Z P. Lagrange structure and dynamics for solutions to the spherically symmetric compressible Navier-Stokes equations[J].Commun Math Phy,2012, 309(2):371-412. [8]LI H L, MASTSUMURA A, ZHANG G J. Optimal decay rate of the compressible Navier-Stokes-Poisson system inR3[J].Arch Ration Mech Anal, 2010, 196(2):681-713. [9]ZHANG Y H, TAN Z. On the existence of solutions to the Navier-Stokes-poisson equations of a two-dimensional compressible flow[J].Math Methods Appl Sci,2007, 30(3):305-329. Global solutions of Navier-Stokes-Maxwell system with large initial data and vacuum KONG Chun-xiang (College of Mathematics and Computer Science, Yan′an University, Yan′an, 716000 China) ∶This work was concerned with the initial boundary value problem of Navier-Stokes-Maxwell system. By means of the classical energy method and some priori estimates, the global spherically symmetric classical solutions for this system were obtained. Here the initial data can be large and initial vacuum is allowed. ∶ Navier-Stokes-Maxwell system; global classical solution; vacuum; a priori estimate 10.3976/j.issn.1002-4026.2017.03.014 2017-05-12 延安大学校级科研计划(YDK2015-46,YDQ2016-22);陕西省教育厅科研项目(16JK1856) 孔春香(1980—),女,硕士,讲师,研究方向为偏微分方程。E-mail;chunxiang1980@163.com O175.2 A 1002-4026(2017)03-0082-06
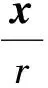



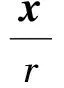


2 先验估计