一种出租车合乘业务方案设计
欧先锋,罗百通,向灿群,黎式南,郭龙源
(湖南理工学院 a.信息与通信工程学院;b.复杂系统优化与控制湖南省普通高等学校重点实验室,湖南 岳阳 414006)
一种出租车合乘业务方案设计
欧先锋a,b,罗百通a,b,向灿群a,b,黎式南a,b,郭龙源a,b
(湖南理工学院 a.信息与通信工程学院;b.复杂系统优化与控制湖南省普通高等学校重点实验室,湖南 岳阳 414006)
以减少出租车的空乘率和乘客等待时间为目标,对出租车合乘方案进行了研究,通过采用K-均值聚类算法和矩阵迭代法解决了乘客合乘问题和最短行程的规划问题,同时还分别对合乘的不同情况进行了分析,探索了车费计算公式,设计了一种与合乘方案相应的合理的车费计算方法,能够兼顾到乘客和司机双方的利益问题,从而提升双方参与合乘的积极性,为出租车合乘问题的研究提供了一些可能的思路。
合乘业务;K-均值聚类;矩阵迭代法;城市交通;车费计算
随着经济的快速发展,城市机动车数量激增,人们的出行越来越方便、快捷,但也带来了交通拥堵、环境污染等一系列问题。其中交通拥堵问题是由于道路资源无法满足人们出行的需要而导致的。合乘方式出行是缓解城市交通拥堵的一种非常简单有效的方法。
出租车合乘业务是指路线相同或相近的2位或多位乘客共同乘坐同一辆出租车出行。系统根据合乘人数、乘车时间、实际路线等因素,分别计算出每位乘客的车费。该业务在不增加运营车辆总数的情况下提高运力,有助于缓解打车难问题,并能降低乘客出行成本,提高司机收入。周和平等[1]以公平性为原则,综合考虑驾驶员与出行者利益,以出行者时间费用成本最小为目标函数,以保障驾驶员合理收益为约束,构建出租车合乘路径选择与费率优化模型,设计改进的遗传算法对该模型进行求解;张薇等[2]针对出租车合乘模式下司机的收入问题,建立了合乘模式下司机收入公平心理模型,采用公平理论分析了司机的心理及行为,通过仿真计算,分析了合乘模式下乘客总需求量及司机公平心理对司机收入的影响;针对城市出租车搭载乘客少、资源大量浪费、造成道路拥堵等情况,张亦楠等[3]设计了一种两段的智能匹配算法(粒子群算法和遗传算法),规划最优的行车路线,以较少的花费和代价,满足尽可能多的乘客搭乘用需求,但算法较复杂。本文对出租车合乘方案进行深入研究,从数学的角度,兼顾乘客和司机双方的利益关系,建立合理的合乘方案模型,分别从乘客-出租匹配、行驶路径规划、车费计算3个方面进行及求解,算法运算效率更快。
1 问题的提出与分析
设计一种高效的合乘方案来合理规划出租车的行驶路径和减少出租车的空载率,使乘客等待时间减少和出租车的利用率提高。出租的合乘主要源于合乘乘客的出发地和目的地与出租车的行驶所经过路径相近或相同,且满足上车点在规定的时间和距离内实现合乘乘客与出租车的合乘。因此在出租车的合乘中,乘客到达上车点的时间与距离是实现出租车合乘成功的关键。
要解决出租车之间的路径规划问题,需要考虑出租车和乘客的起始点和目的地的不同,求解最短路径问题,设计合乘方案全面兼顾乘客与司机的花费和收益,合理进行行车路线规划,提高运送效率,尽可能地减少所有乘客从出发点到达目的地的乘车时间。同时要使所需的出租车数量尽量少[1],即减少出租车的空载率。也即出租车的行驶路径上尽可能地出现3人合乘的情况,而乘客则要尽可能地选择只有1个空位的出租车。
合乘方案与乘客、司机双方的经济利益息息相关,有效保障两方的经济花费和收益对能否良好实施合乘方案非常关键,所以选择合理的车费计算方法至关重要[2]。在多名乘客共同乘坐的路段,每位乘客仅需花费低于单独乘车时的车费,在出租车行驶路径规划合理的情况下(不绕路或者合理绕路),采用合乘的方式应该有效地减少乘客的乘车花费,适当增加司机的收益。不绕路是指路径规划的最短路径。合理绕路是指出租车载着乘客A驶向目的地的过程中,绕行一段距离接乘客B。此过程会对乘客A造成一定的损失,需对计费方式进行适当调整,对损失进行补偿,保证乘客和司机的经济利益,使乘客付出的车费少于不绕路付出的车费,同时司机的收费多于不绕路的收费。在不绕路计费过程中,合乘方案的车费计算应对某乘客超出起步距离的单独乘车段距离、2人合乘段距离、3人合乘段距离进行统计和距离累计,还有等车时间损失等问题,对司机而言,还需考虑候时费、长途返空费等问题。在合理绕路计费过程中,除考虑上述因素外,还需考虑被绕路乘客的绕行损失、司机中途停车等候等问题,为体现公平性,还需对司机和乘客进行补偿。
2 出租车合乘方案的数学模型建立
本文针对出租车合乘匹配问题,提出了解决思路,如图1所示。首先对乘客进行分配,按照起点、终点方位分布情况和乘客各自需求,求出车辆行驶时的最优搭乘半径,将乘客分配到合适的出租车上;然后再对分配到同一辆车上的多名乘客的行驶路径进行合理规划,找出一条合理的行车路线。这样能够帮助有需求的乘客搭乘到适宜的出租车。通过使用现实数据验证表明,该算法能够达到多名乘客共同搭乘出租车的目标[3-4],并应用到现实生活中去,有效提高出租车空间资源的利用率,减少乘客等待时间和出租车空载率,实现各方利益的最大化。

图1 出租车合乘匹配问题解决思路
2.1 乘客分配
2.1.1 乘客分配模型建立思路
如图2所示,在分配乘客到出租车的过程中,采用K-均值聚类算法,按照起点、终点方位分布情况和乘客需求,规定以出租车为中心的最佳搭乘半径r(比如250 m)画一个圆形区域,将区域内符合要求的乘客划分到一辆出租车上(假设限坐3人),比较车上乘客各自的目的地方向的夹角,若某一乘客的目的地方向与其他乘客的目的地方向的夹角大于角度α,则该乘客下车;出租车再在r范围内重新寻找乘客,直到满载3个乘客或r范围内无合适乘客。然后再以剩下没上车的乘客为中心规定半径,将半径内有空位的出租车划分给没上车的乘客,再进行乘客目的地方向夹角比较,实现乘客和出租车的匹配划分,为后续的路径规划做准备工作。

图2 聚类规则
2.1.2 乘客分配过程描述
本文的研究对象有多辆出租车和多位有搭载需求(同意合乘)的乘客,出租车应该在不超过最大载客容量(本文假设限定3人)的情况下,满足乘客各自搭乘需求的同时,规划合适的行驶路径,尽量多地搭载符合要求的乘客,而且还要保证总共行驶的时间最短[4],其算法如图3所示。
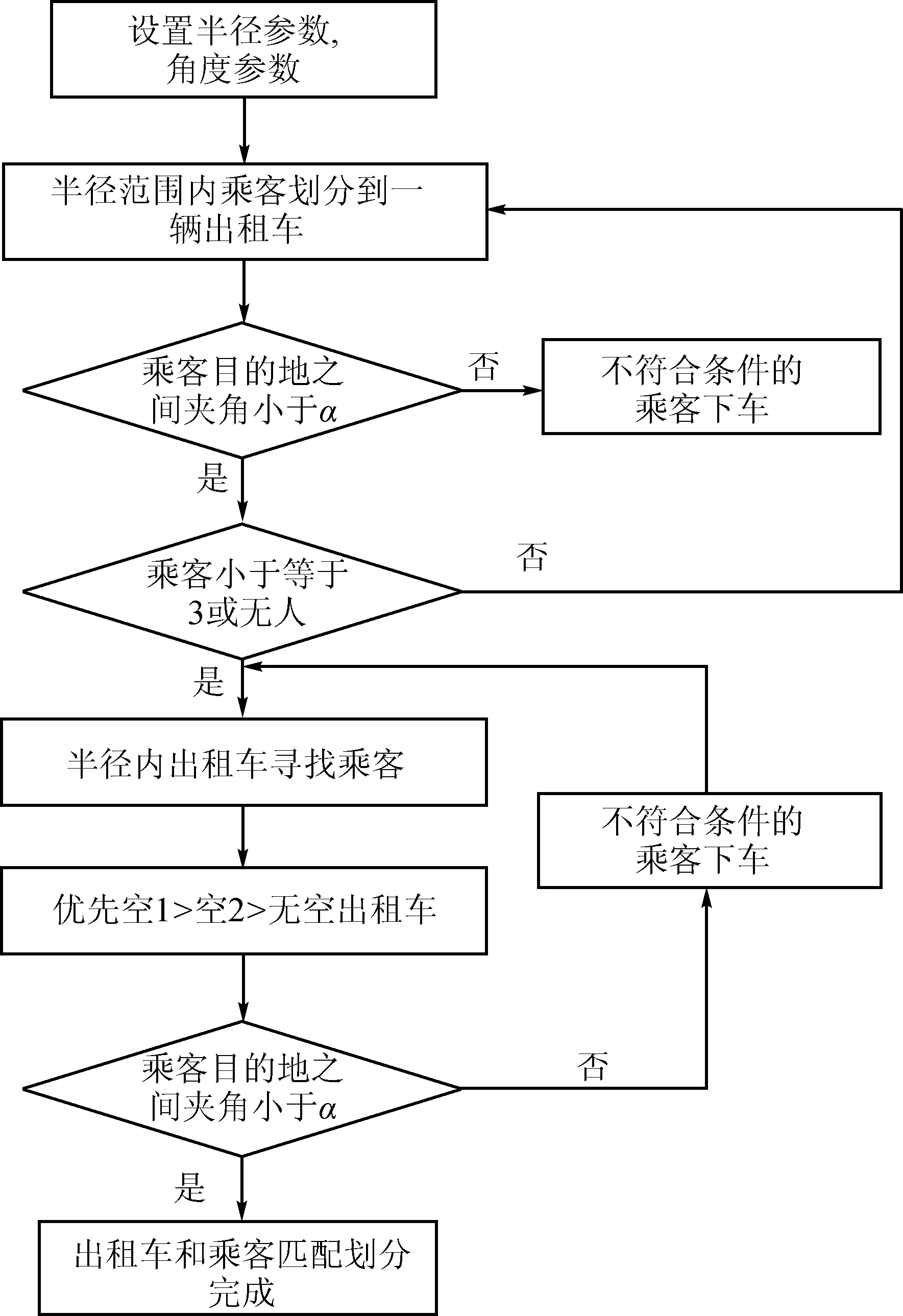
图3 乘客与出租车分配算法流程图
在此过程中,关键问题是要计算得到出租车在每个停车点的搭载区域,也就是以出租车行驶路径上的每个节点(出租车位置、乘客起点、终点)为中心的圆形区域(规定半径)。根据初始情况时,各节点附近的出租车搭载情况和乘客各自的搭乘需求,运用K-均值聚类算法,以成功匹配率作为目标优化函数,经过多次迭代计算获取最合理的搭乘半径,达到搭载率最大的目的。乘客分配过程中的目标函数为:
(1)
其中:f(xk)指出租车k在运营时的匹配率;Mk指出租车k在运营过程中成功匹配的乘客数; nk指出租车k在刚开始的行车路线中应途经的节点总数;sk,n指出租车k的第n个节点在其搭载区域内所含的乘客上、下车节点数量。
2.1.3 约束条件
出租车搭载乘客时,任何时刻都要符合车上共同搭乘的乘客数目不超过规定的最大载客容量。即:
(2)
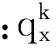
乘车过程中,乘客的上、下车行为一定要发生在同一辆车上,即在上车点x至下车点m+n+x的路上一直坐在同一辆出租车上,若不然,则视为不能匹配成功。于是有:
(3)
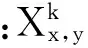
2.2 出租车智能合乘匹配中的行驶路径规划
路径规划问题是对已经划分到同一辆出租车上的乘客,采用矩阵迭代法来对节点距离矩阵进行迭代运算求解到达乘客目的地的最短行驶路线,在运营出租车的数量尽量少的情况下,成功搭载尽量多的乘客,同时将行驶时间降到最小。
矩阵迭代法[5-6]主要是通过不断迭代计算、更正原路径权矩阵D而达到逐步向最短路径权矩阵D0接近的目的,最后获得最短路径权矩阵D0,其计算公式为:
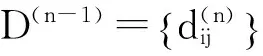
(4)

其运算规则为:
(5)
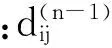
通过式(4)、(5)屡次迭代计算,直到满足D(n)=D(n-1),即第n次迭代后的路径权矩阵的每一元素与第(n-1)次迭代后的路径权矩阵中对应元素全部相等,那么矩阵D(n-1)就是最短路权矩阵D0,即D0=D(n)=D(n-1),再根据式(5)计算路权矩阵的同时可得到路径矩阵。
首先应构建路径路权矩阵(以距离为权的权矩阵),该矩阵表明了节点间只经过一步(一条边)抵达某一点的距离,对距离矩阵进行屡次迭代计算,获得需通过两步抵达某一点的最短距离。所以,规划出租车行驶的最优路线时,应该计算获取每个停车节点之间的最短路线。本文采用距离矩阵求解最短路径的方法[7]。
2.3 出租车合乘方案的计费方式
减少支付车费即能抵达目的地是提高乘客选择合乘方式出行的积极性的关键,为合乘方案设计合理的计费方式则能相应地减少乘客所需支付的车费。而且由于秉持公平的原则,应该保障出租车司机的经济收入。因此,确定一个合理的合乘费率标准是本文提出的合乘方案能够顺利实施的关键因素。确定合乘费率所需要达到的目的,就是在不少于司机按正常费率行驶完全程所得收益的同时,使每个乘客的所需支付车费降到最少[8]。
2.3.1 合乘费用
令出租车的起步价为ps元,超过起步价后,每车公里租价为pr元,乘客i的行程为xi。当乘客i单独搭乘出租车时,其支付车费p(xi)为
(7)
在乘客选择合乘方式搭乘出租车抵达目的地的过程中,会遇到各种各样的合乘方式。比如,乘客可能有同一个起点,而终点却不同;乘车途中又可能有其他人上车(不超过最大限载容量即可)。然而不论哪种合乘方式,对选择合乘的乘客而言,在其从起点至终点的完整乘车过程中的乘车状态可分为2种:合乘状态和独乘状态。同一出租车上每位乘客在搭乘时,别的乘客开始搭乘或抵达终点都会导致其乘车状态的变化,即乘客合乘出租车的过程也是其乘车状态不断改变的过程[9]。令乘客i搭乘出租车的路程长度为xd,与其他乘客合乘总路段为di,合乘路段所需支付车费的比例(简称支付比例)为θ,乘客i的乘车费用可用式(8)表示。
式(8)中的(a)式表示乘客i全程合乘的费用;(b)表示乘客先与人合乘di,再独乘至终点所需费用;(c)表示先独乘,且独乘路程超过起步价里程b的情况下,再与人合乘di所需费用;(d)表示先独乘,且独乘路程不超过起步价里程b的情况下,再与人合乘di所需费用;(e)表示乘客先独乘yi的路程,且独乘路程超过起步价里程b的情况下,再与人合乘di,最后又独自乘车直至终点所需的费用;(f)表示乘客先独乘yi的路程,且独乘路程不超过起步价里程b的情况下,再与人合乘di,最后又独自乘车直至终点所需的费用;(g)表示乘客先合乘zi的路程,且合乘路程超过起步价里程b的情况下,再独乘li,最后又与人合乘直至终点所需的费用;(h)表示乘客先合乘zi的路程,再独乘li,且此时乘车路程不超过起步价里程b的情况下,最后又与人合乘直至终点所需的费用;(i)表示乘客先合乘zi的路程,且合乘路程不超过起步价里程b,再独乘li,且此时乘车路程超过起步价里程b的情况下,最后又与人合乘直至终点所需的费用。
(8)
2.3.2 可预见损失补偿
出租车计费方式应该具有公平性、双赢性,避免打击司机、乘客选择合乘出行的积极性,不利于合乘方案的实施和推广[10]。实际合乘中,难免会遇到乘客增加绕行距离、司机中途停车接客等问题。因此,应对司机和乘客可预见的损失进行补偿。本文主要是对乘客的绕行补偿。
Jr=0.5·c·(F2-F1)
(9)
其中:Jr为乘客因合乘而产生的绕行距离补偿/元:c为超过起步里程后的每公里单价/(元/km):F1为乘客单独乘车的最短距离/km,由合乘方案模型中矩阵迭代法在乘客输入乘车起终点后自动算出;F2为乘客合乘的实际距离/km。
2.3.3 出租车合乘方案的计费方式的模型
根据求出的乘客i的乘车费用ci,考虑到绕行损失补偿,则合乘方案的计费模型为:
pi=ci-Jr
(10)
3 实验分析
3.1 实验参数设置
实验参数的设置为:合乘率r=0.9;车配人半径R1=0.25 km;人配车上座优先参数[2,1,0];人配车半径R2=0.5 km。
算法过程:
while(合乘率>0.9)
{上车过程:
1)车配人。在半径为R1=0.25 km内的人随机上车,每辆车尽量坐满3人。
下车过程:
2)人车配对。根据给出的约束条件对每辆存在合乘的车辆进行人人配对,配对成功则合乘,否则不合格的人下车。
3)人配车。未上车的乘客搜索半径为R2=0.5 km内车辆,根据搜索范围内车辆上座率作排序,优先上存在乘客的租出车,增加合乘率。
4)计算合乘率及相关参数}
结论:R1、R2越大,合成率越高;上座优先参数为[2,1,0]时合乘率最大,[1,2,0]次之。
3.2 实验数据
为了对模型和算法进行验证,收集某城市的部分打车需求数据、空驰出租车的位置信息,假设路网为正方形网格,道路可双向行驶(以一车3乘为例),其中空驰出租车的位置信息如表1所示。

表1 出租车车辆信息
合乘乘客信息如表2所示。

表2 乘客信息
3.3 实验结果分析
根据起始位置和目的地能否起到路径优化的作用,由本文的算法得到如图4所示为6,34,55,150,239,345号车对3人共乘时的车配人仿真结果。

a.6,34,55号车辆上3人共乘车配人结果

b.150,239,345号车辆上3人共乘车配人结果
最终出租车行驶过程中搭乘乘客路线见表3。

表3 出租车行驶路线
图5显示了数据中不同合乘情况时,合乘起点初始位置和随后的城市路网最优路径。图中左边一列坐标是以左下角为基点,右边一列坐标是以左上角为基点。
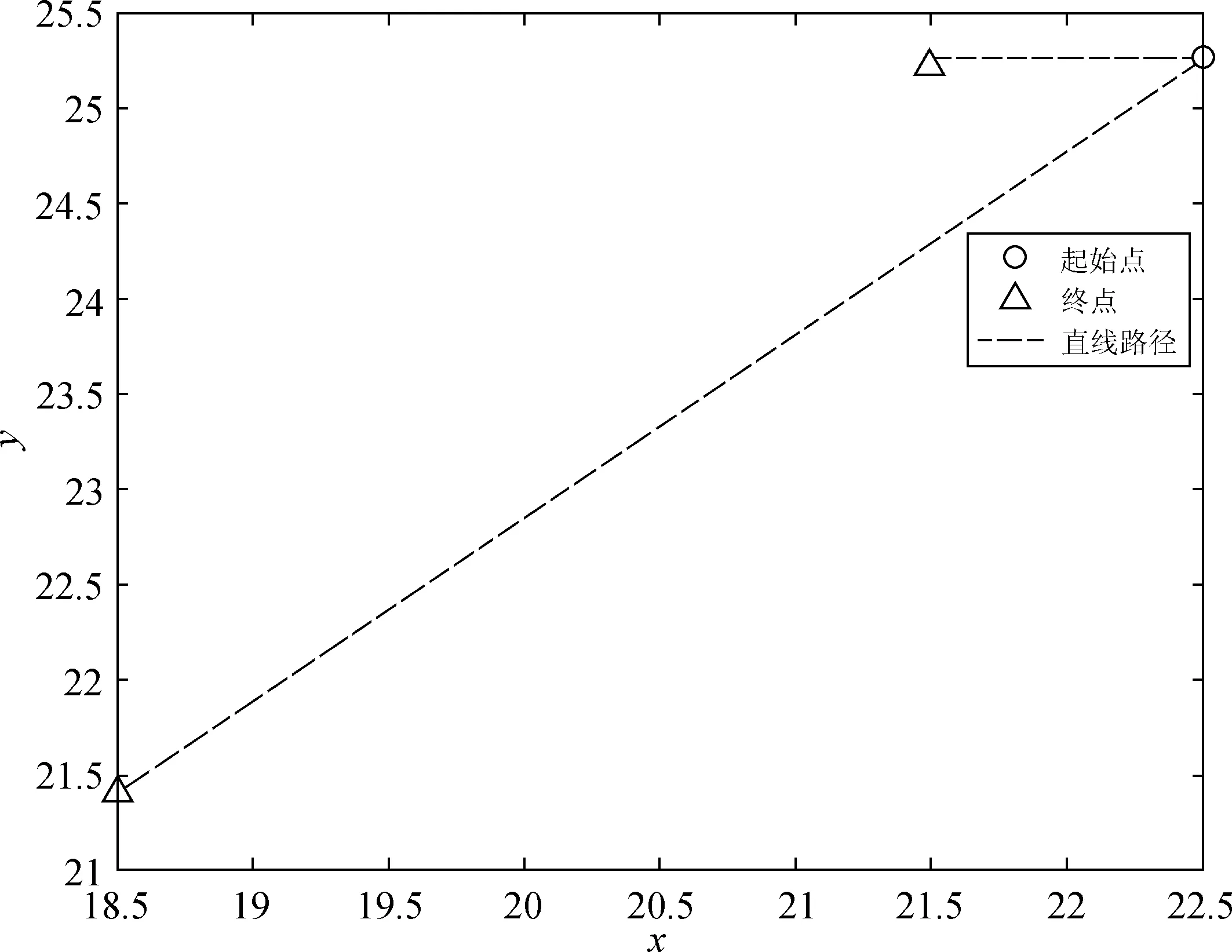
a.2人合乘同起点起始位置分布图

b.2人合乘同起点网络最优路径

c.2人合乘不同起点起始位置分布图

d.2人合乘不同起点网络最优路径
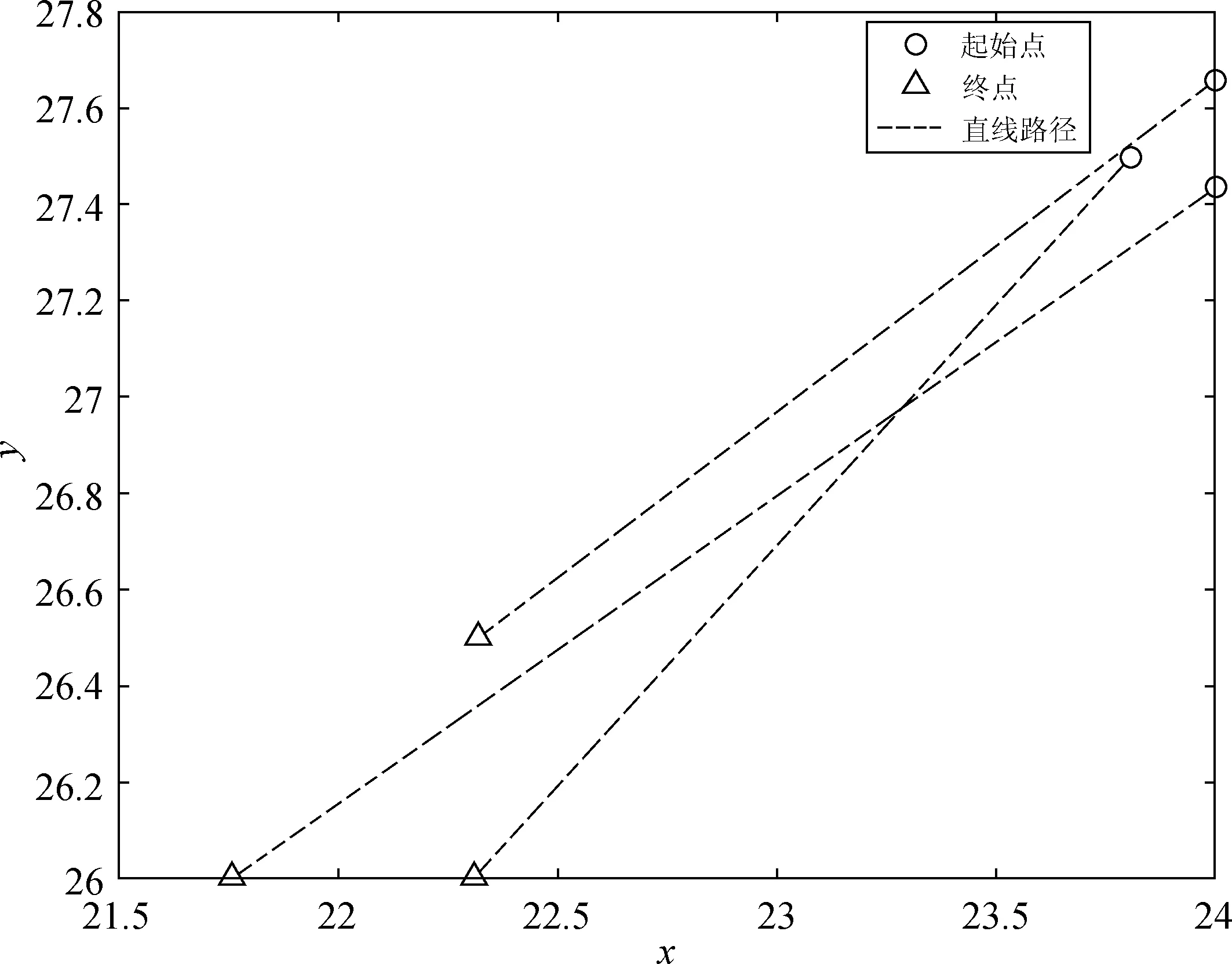
e.3人合乘同起点起始位置分布图

f.3人合乘同起点网络最优路径图5 合乘起点初始位置和城市路网最优路径图
根据本文中提出的车费计算模型得出某出租车在3人合乘情况下的车费支付情况如表4和出租车司机收益情况如表5。

表4 各乘客在不同乘车方案下的车费支付情况 元

表5 出租车司机在不同乘车方案下的收益 元
4 结语
本文在充分考虑乘客和司机各自需求的前提下,优化设计了一种高效的出租车合乘方案模型。该模型充分考虑了乘客的需求(等待时间尽量短,乘车价格尽量少)和司机的需求(空车等待时间少,收益明显增加),通过对出租车合乘方案的设计问题进行分析研究,将相关问题及约束条件采用了数学语言描述,针对方案设计过程中遇到的关键问题,采用两段式解决的办法,采用基于K均值聚类、矩阵迭代法的优化模型,实现了合乘路线最优的目标。
本文设计的出租车合乘方案模型,在用尽量少的出租车搭载数目尽量多的乘客,同时使合乘总花费达到最少。采用2个算法(K均值聚类、矩阵迭代法)分阶段解决了合乘匹配和路径规划的难题。最后运用所提出的出租车合乘方案模型对附件中的实际数据进行了分析验证,结果表明:该能模型能有效解决附件中出租车合乘调度问题。但仍存在一些不足,如在车与人的匹配问题,会出现有一个车或者几个车在每一个停靠站点都有一个人下车,而另外一些车在这一路一直是空载等问题有待完善和改进,使合乘方案更加合理、高效。如本文在研究合乘匹配问题中加入的约束条件不够全面,因为在现实生活中还需考虑道路拥堵情况,天气环境因素等影响,使合乘方案更贴近现实。
[1]周和平,钟璧樯,彭霞花,等.出租车合乘路径选择与费率优化模型[J].长沙理工大学学报(自然科学版),2011,8(1):20-24.
[2]张薇,何瑞春,肖强,等.合乘模式下司机收入公平模型及仿真[J].交通运输系统工程与信息,2015,15(4):92-98.
[3]张亦楠,魏志强,刘昊.出租车多人合乘匹配问题的研究[J].信息通信,2014(3):70-71.
[4]张亦楠.出租车合乘模式下的智能匹配问题的研究与实现[D].青岛:中国海洋大学,2014.
[5]刘洪丽,顾铭.矩阵迭代法在物流中心选址中的应用分析[J].现代商贸工业,2013(20):64-66.
[6]刘洪丽,冯伯林.基于最优化思想的城市交通流分配[J].武汉理工大学学报(交通科学与工程版),2005,29(6):913-916.
[7]郭瑞军,王晚香.基于矩阵迭代法的出租车合乘最短路径选择[J].大连交通大学学报,2011,32(4):28-31.
[8]覃运梅,石琴.出租车合乘模式的探讨[J].合肥工业大学学报(自然科学版),2006,29(1):77-79.
[9]刘佳.租车合乘方式及定价模型优化研究[D].重庆:重庆交通大学,2016.
[10]丁冉.出租车动态合乘匹配问题研究[D].南京:东南大学,2015.
[11]肖强,何瑞春,俞建宁,等.出租车合乘收益趋势影响模型研究[J].兰州交通大学学报,2016,35(4):141-147.
[12]CHORFIi H,ALATEE A,ALOQEELY A,et al.A smart real-time ride-share for riyadh city[J].Procedia-Social and Behavioral Sciences,2015,195:1932-1937.
[13]FAHNENSCHREIBER S,GüNDLING F,KEYHANI M H,et al.A multi-modal routing approach combining dynamic ride-sharing and public transport[J].Transportation Research Procedia,2015,13:176-183.
Design and Research of Taxi-pooling Service
OUXianfenga,b,LUOBaitonga,b,XIANGCanquna,b,LIShinana,b,GUOLongyuana,b
(a.College of Information & Communication Engineering;b.Key Laboratory of Optimization & Control for Complex Systems,Hunan Institute of Science and Technology,Yueyang 414006,China)
To reduce the passengers’ waiting time and the taxis’ unloaded ratio,the authors studied the problem of taxi-pooling,solved matching problem between vehicles and passengers,and minimized the taxi route through K-means clustering algorithm and matrix iteration method.At the same time,they explored the formula for calculating fare based on the analysis of different conditions of taxi-pooling,then put forward a reasonable pricing optimization model considering the benefits of both the taxi driver and passengers,which would increase the participation of the two parties.This proposed algorithm presented some feasible ideas on the research of taxi-pooling and the allocation of taxi resources,which was beneficial for improving urban traffic conditions.
taxi-pooling;k-means clustering;matrix iteration method;urban traffic;fare calculation
10.13542/j.cnki.51-1747/tn.2017.02.010
2017-05-18
湖南省自然科学基金项目(2017JJ3099);湖南省科技计划项目(2016TP1021)
欧先锋(1983—),男,讲师,博士,研究方向:图像处理、视频压缩编码及传输。
郭龙源(1973—),男,副教授,博士,研究方向:计算机视觉、图像处理,电子邮箱:goulongyuan@hnist.edu.cn。
TP391
A
2095-5383(2017)02-0043-07

