用SIFT算法实现铁路扣件图像分类
王 强
(1.成都工业学院 机械工程学院,成都 611730;2.西南交通大学 机械工程学院,成都 610031)
用SIFT算法实现铁路扣件图像分类
王 强1,2
(1.成都工业学院 机械工程学院,成都 611730;2.西南交通大学 机械工程学院,成都 610031)
基于图像特征点的匹配是解决很多问题的关键,不同的应用场景有不同的要求。研究SIFT算法在进行匹配的参数选择问题,结合随机抽样一致集算法(RANSAC),剔除错误的匹配,分析参数选择对匹配结果的影响,研究不同尺寸图像特征点生成关系。针对SIFT算法对光照的敏感性问题,通过图像增强再进行匹配,结合位置信息,实现了特征点数量较少的小图像铁路扣件图像的分类。
SIFT算法;图像分类;参数选择;位置信息;特征
图像特征点检测和匹配在计算机视觉图像方面的应用广泛,包括纹理分类[1-2],运动物体跟踪[3],人脸识别[4],人脸检测[5]等。特征点检测的准确性直接关系到最终的图像处理结果,因此图像特征点的检测一直是研究的重点。通过检测图像局部特征点,对不同图像中的同一物体进行匹配。早期的特征点检测方法有Moravec[6]提出的基于角点检测的视频图像匹配算法。Harris等[7]提出了利用图像梯度的角点检测算法。Rosten等[8]提出了FAST特征点检测算法,通过比较中心像素与邻域像素的大小,然后计算得分值来检测特征点。Calonder等[9]提出了BRIEF特征点检测和匹配算法,准确地说BRIEF是一种特征描述算法,采用汉明距离进行特征配对来对特征点进行描述。Rublee等[10]提出了结合BREIEF和FAST算法的ORB检测算法,结合了图像特征点的检测和方向描述。Leutenegger等[11]提出了BRISK检测算法,在图像多尺度上主要利用FAST算法进行特征点检测。1999年,Lowe[12]提出的SIFT(Scale-invariant feature transform,尺度不变特征转换)算法,2004年对算法进行了完善[13]。Bay等[14]在SIFT算法的基础上提出了快速鲁棒特征Surf算法;Ke等[15]在SIFT算法的基础上结合主成分分析提出了PCA-SIFT算法。基于图像局部特征的研究一直是广大科研人员研究的重点,如何准确找出图像局部的特征,是用于图像后续处理的关键。Ojala等[16-17]结合图像局部特征提出了局部二值模式(LBP)算法;Davarzani等[18]提出了尺度和旋转不变性的LBP算法用于人脸识别;Geng等[19]提出了SIFT特征用于人脸识别;Ren等[20]提出了抗噪声的LBP编码方法用于提高人脸识别的识别率。这些方法首先都需要实现图像的匹配。比如人脸识别,对一个人从不同角度进行图像采集,通过检测特征点,实现不同角度同一个人的人脸识别等。Mikolajczyk等[21]比较了各种图像局部感兴趣区域的检测算法,主要从特征点的检测和图像匹配两方面进行比较,得出SIFT算法是一种比较好的检测和匹配算法的结论。
由于光照、尺度、角度等因素的影响,对同一物体的多次采集的图像都会出现不同的效果。SIFT算法由于采用了多尺度进行关键点检测,同时,对特征点的描述采用了128维方向向量,在尺度不变性和旋转不变性方面的表现是非常优秀的。在采用SIFT算法的时候,对图像关键点检测以及图像匹配的参数选择是至关重要的。Lowe虽然提出了SIFT算法,但在参数选择上却没有明确给出选择方法,也没有说明图像尺寸对特征点数量的影响,导致在使用SIFT算法时,往往不能得到预期的效果。本文结合理论分析和实验验证,确定了特征检测参数与特征点检测结果关系以及匹配参数与匹配率之间的关系,给出了SIFT算法几个重要参数的选择原则。SIFT算法对光照的变化有一定的敏感性,采用128维的向量归一化描述方法可以避免线性光照的影响,但是对于非线性光照的影响却不能够消除。现实中采集的图像往往受到各种光照条件的影响,比如自然光和采用光源采集的图像,其光照条件是完全不一样的;在自然环境中,不同天气采集的图像也是完全不同的。同时,物体本身对光照的反射强度也将影响到图像采集效果,最终影响图像特征点的匹配。如果对同一类物体在不同条件下采集的图像进行识别而不是对同一个物体从不同角度采集的图像进行识别,则光照条件将成为关键因素。本文针对光照不均以及小图像采用SIFT算法检测的特征点数量较少问题,提出了增强光照方法以及添加特征点位置信息方法,实现了铁路扣件图像的分类。
1 SIFT和RRANSAC算法原理
1.1 SIFT算法原理
SIFT算法是一种多尺度、旋转不变性、仿射不变性图像特征点检测算法。SIFT算法主要分为以下5个步骤:
1)利用高斯模糊建立多尺度高斯金字塔;
2)利用高斯差分(DOG)算子进行极值点检测;
3)通过边界抑制去掉边界影响,通过极值抑制去掉对比度小的极值,通过拟合三维二次函数确定亚像素精度的极值,得到稳定的极值点;
4)计算在极值点16×16邻域范围内梯度直方图,将16×16范围分为16个4×4的像素块,每个块计算8个方向的梯度直方图,得到关键点的128维描述向量并归一化消除光照影响;
5)图像进行匹配时,比较两图中的关键点128维向量的欧式距离,Lowe[12]提出:比较最近距离与次近距离之间的比值,如果小于0.8则认为找到匹配点。
SIFT算法首先利用高斯卷积核构造对尺度图像金字塔,Lindeberg等[22]已经证明高斯卷积核是实现尺度变换的唯一线性核。对于二维图像I(x,y),利用高斯卷积核在尺度空间进行图像卷积的定义为:
I(x,y,σ)=G(x,y,σ)*I(x,y)
(1)
(2)
其中:G(x,y,σ)是尺度可变的高斯函数;(x,y)是坐标;σ是可变尺度坐标。通过改变σ的大小,实现不同尺度的图像。σ的大小决定图像模糊的程度,越大图像越模糊,细节特征越不明显;反之,则反映图像的细节特征。在不同的尺度空间根据DOG算子与LOG算子的近似性,用DOG代替LOG对图像在三维空间26点邻域内进行特征点检测,加快了特征点检测的速度。DOG算子定义为:
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))*I(x,y)= I(x,y,kσ)-I(x,y,σ)
(3)
其中k表示高斯尺度按比例变化的系数。
由于DOG算子有明显的边界响应,因此采用Hessian矩阵抑制边界去掉不稳定的极值点,同时,对于对比度比较小的极值点,通过设定阈值进行抑制。最后拟合三维二次函数,通过求取二次函数的极值,达到亚像素精度,得到稳定的极值点,即图像中的特征点。再对特征点进行描述,得到特征点的唯一表示,通过比较描述算子的相似性,确定不同图像中相同的特征点,从而实现图像匹配。SIFT的描述算子采用128维的方向直方图实现。
1.2 RANSAC算法原理
RANSAC(RANdom SAmple Consensus,随机抽样一致)算法称为随机抽样一致集,由Fischler等[23]在1981年提出。它通过迭代的方式,从一组观测数据中估计数学模型的参数。假设数据的分布可以用一个数学模型来解释,通过输入数据计算出模型的参数,不能适应模型参数的数据称为局外点;反之,称为局内点。如果输入数据中有足够多的点被归为局内点,说明估计的模型是合理的。重复这个过程,每次产生的模型如果局内点太少就摒弃,如果比现有模型更好就选用这个模型代替现有模型。如图1所示,两组观察数据点云可以通过RANSAC算法让两个点云匹配。首先随机得到一个点云中的点对,利用两点关系(比如方向、夹角等)搜索另一个点云中的点对,然后计算旋转和平移参数,通过变换找到其他点并重新计算旋转和平移,重复上述过程最终找到点云匹配的位置。

图1 RANSAC算法匹配点云示意图
RANSAC算法在SIFT算法中的应用主要是筛选出SIFT算法中的错误匹配点。首先从特征点集中随机选取4个匹配点对计算变换矩阵。根据误差度量函数计算满足当前变换矩阵的元素个数,判断是否是最优一致集,若是则更新当前最优一致集。重复迭代,直到当前的错误概率小于最小错误概率。图2是采用RANSAC筛选前和刷选后的SIFT特征匹配对比图,可以看出,采用RANSAC算法把错误的匹配过滤掉了。

图2 RANSAC用于SIFT匹配
2 SIFT算法参数选择
2.1 SIFT参数对图像特征的影响
SIFT算法中需要确定的参数包括高斯模糊尺度σ,边界抑制阈值Curv_thr,低对比度抑制阈值Cont_thr以及128维向量的最近距离和次近距离之间的比率R。Curv_thr主要是去掉边界影响,因为DOG算子有较强的边界效应。由于SIFT算法是检测在三维空间中的极大值或极小值,已经可以去掉大部分的边界影响,所以这个参数对整体特征点检测的影响不是很大,通过实验发现,Curv_thr设置为0,10,20对特征点数量的影响都不是很大。Cont_thr是为了去掉与邻域之间低对比度的特征点,阈值设置的大小与特征点的数量有很大的关系,尤其是图像灰度分布在比较小的范围内的时候,对最终图像特征点的数量很大的影响。此外,高斯模糊尺度σ对特征点的检测有至关重要的影响,相似性比较的比率R对特征点匹配有关键的影响。
1)高斯模糊尺度σ。σ主要用于生成多尺度图像金字塔的,利用DOG进行特征点检测。σ的选择决定了图像的模糊程度,σ越大图像越模糊,σ越小越能表现图像的细节特征。高斯模糊是根据二维高斯分布函数计算出来的。二维高斯分布的函数如式(4)所示,其函数图像如图3所示。
(4)
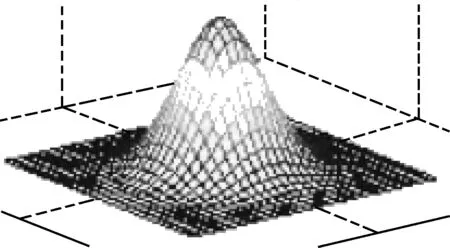
图3 二维高斯函数图像
σ也称为高斯模糊半径,σ越小曲面越高越尖,检测出来的特征点也越多,反之曲面越低越平缓,特征点越少。根据高斯3σ原则,分布在±3σ范围内的概率为99.73%,因此超过±3σ的范围可以认为接近于零而不予考虑。高斯模糊实际上包括了图像的高斯低通滤波处理,消除了噪声对特征点检测的影响。因此,SIFT算法是抗噪声的。图4是来自Miko-lajczyk and Schmid 2005图像数据库中的Boat图像,图a是原图,后面是分别加上不同程度的高斯噪声后的结果。从表1看出,噪声对图像特征点的检测没有太大影响,σ的值不同影响是相当大的。检测出来的特征点数量有明显的区别。随着σ值增大,特征点的数量减少比较多。表1中Cont_thr值都设置为0.04。随着特征点数量的增加,整体花费的时间也相应增加。

图4 不同高斯噪声图像
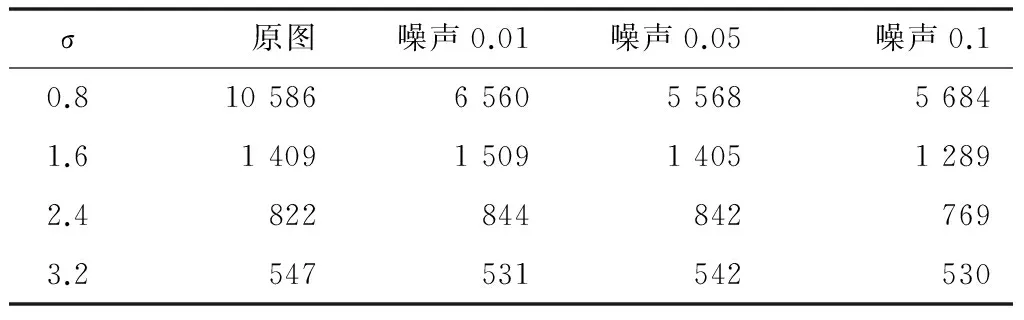
表1 不同σ值特征点检测数量
2)描述算子相似性比较的比率R。SIFT算法的特征点相似性比较采用的是最近距离与次近距离之间的比率来判断的,距离的计算采用欧式距离。这个值的大小将影响图像匹配点的数量。如果值较大,则匹配的点越多,但是错误的匹配也相应增加,同时增加了匹配的时间。反之,值越小匹配点减少,有可能导致没有匹配点。
对于图像匹配而言,并不是匹配点越多越好,理论上如果不考虑误差的影响,对于二维图像而言,如果匹配的结果用于图像拼接,只要找到两个相同的点,就可以实现完全拼接。如果用于图像识别,则主要考虑识别的准确性。如果识别的对象单一、背景简单,则需要匹配的数量很少就可以实现;反之,则需要增加匹配点。物体在现实中都有明确的边界特征,如果能够找到每个物体有代表性的特征,则不需要太多的匹配点就可以实现物体的识别;反之,匹配点太多则将增加运算时间,对于很多需要满足实时性要求的时候则不能达到。图5显示了匹配数量与R的关系图,图6显示了匹配数量与运行时间的关系。在假设RANSAC后的点是正确的匹配点的前提下,从图5也可以得出匹配率与R之间的关系图。表2显示了Miko-lajczyk and Schmid 2005图像库中的两幅Boat图像的匹配结果,两图拍摄的角度不同,采用σ=1.6,Cont_thr=0.04,不同的R进行匹配的结果,图像大小为850×680。
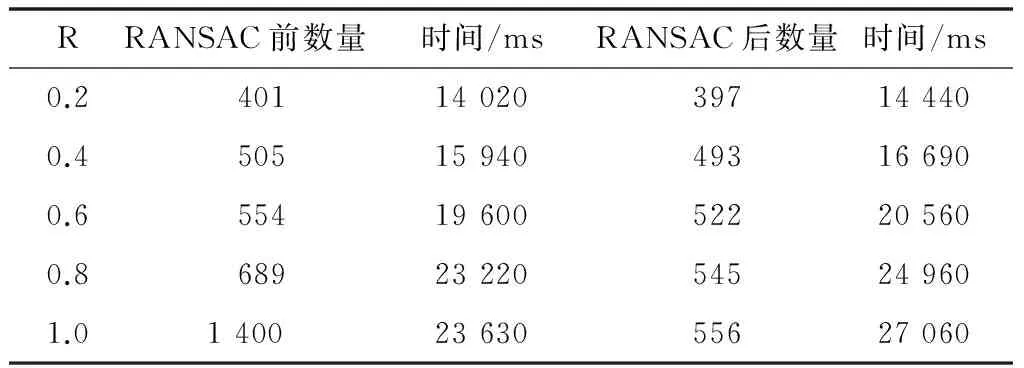
表2 不同R值的匹配结果
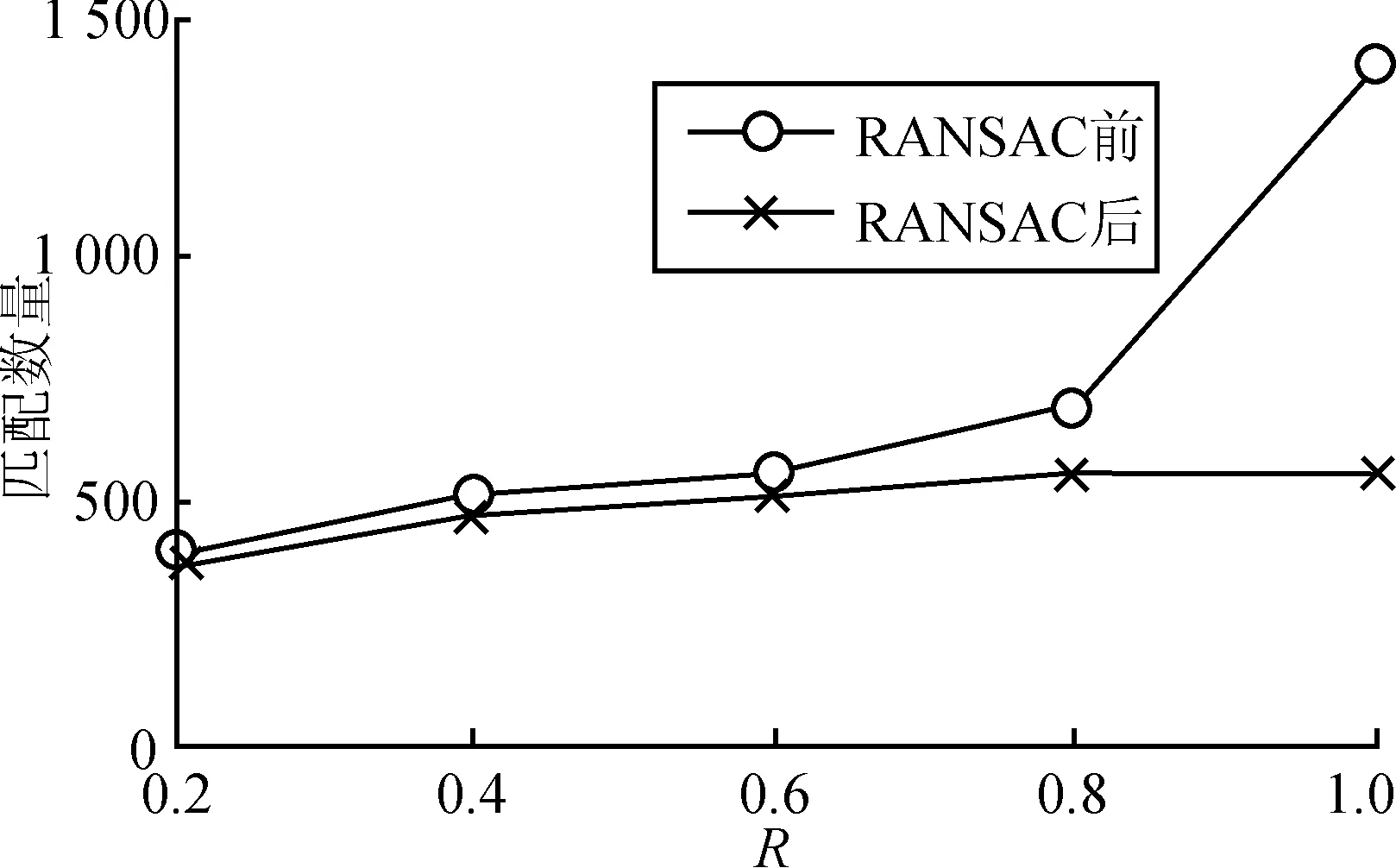
图5 R和匹配率关系
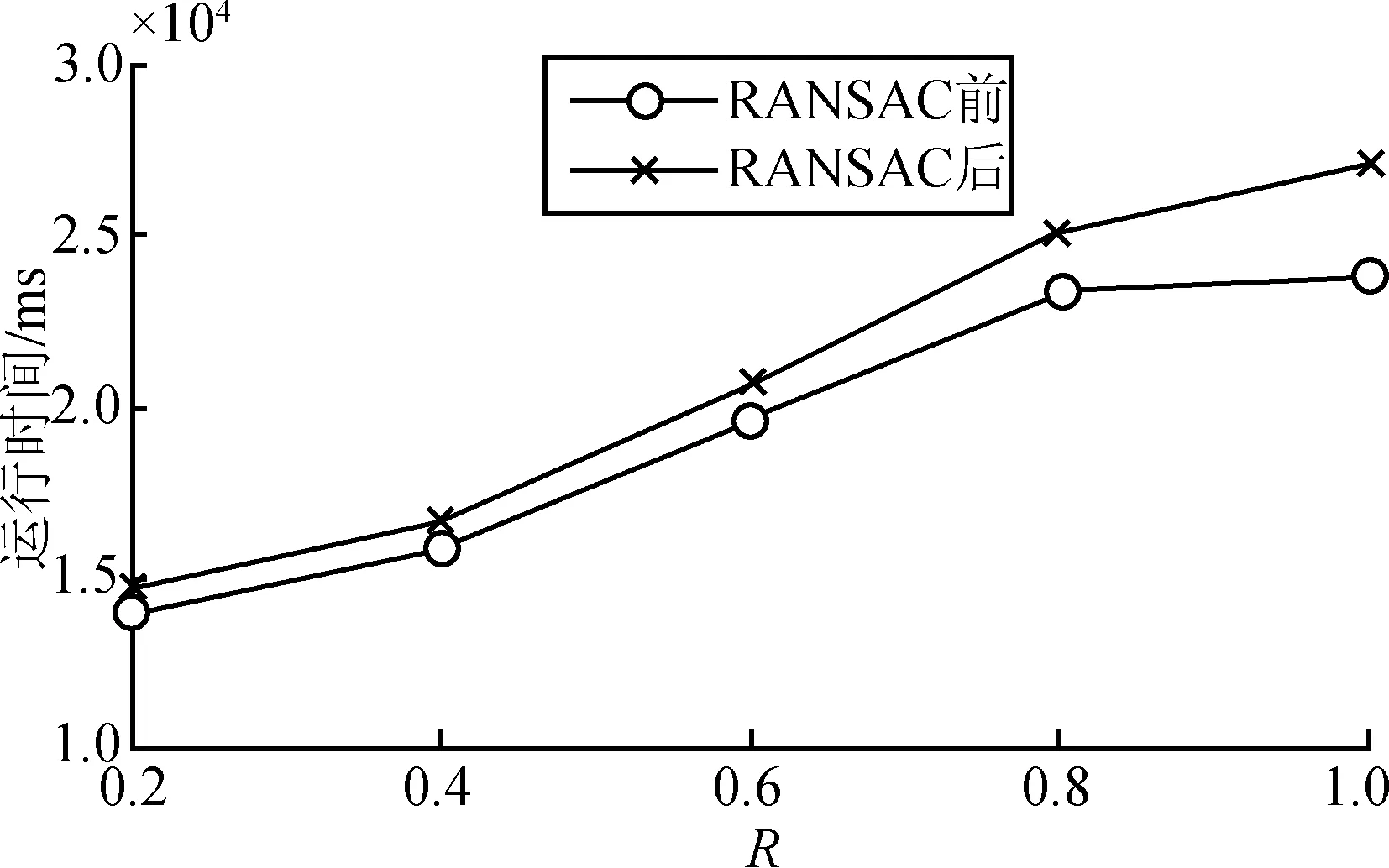
图6 R和运行时间关系
从表2以及图5和图6可以看出,随着R值的增大,匹配点的数量也在增大,同时错误的匹配点也在增加,时间也逐渐延长。从实时性方面考虑,在采用SIFT算法的时候,应该在保证匹配可靠的前提下,尽量减小R的值。
从σ和R的值来看,σ主要影响图像特征点的检测数量,点的数量随着σ值的增大而减少。而R主要影响匹配点的数量。针对不同的图像这些值的选择是不同的,比如对于图8显示的是一幅180×120的铁路扣件图像,如果采用σ=1.6和R=0.8,则不能找到正确的匹配点。Lowe推荐的R=0.8在实际匹配中出现了很多错误的匹配,而且时间上也花费比较多,从实际效果来看,R选择在0.2到0.6是比较合适的。R=0.2可以用于匹配精度要求比较高的匹配,而R=0.6则用于匹配点数量比较多的情况。在实际应用中,应该根据需求自主选择R的值或者采用自适应的R值来实现图像匹配。
2.2 图像大小对特征的影响
SIFT算法采用多尺度高斯金字塔来检测特征点,对于特征点的描述采用16×16邻域像素的梯度方向直方图实现。由于小尺寸的图像建立高斯金字塔的数量有限,同时特征点的描述区域也受限制,导致图像大小对特征点的数量有很大影响,进而影响匹配数量。图7是Miko-lajczyk and Schmid 2005图像库中的两幅Boat图像,原图大小850×680。对原图采用SIFT算法,以及对原图依次采用双线性插值缩小一半再采用SIFT算法的检测结果见表3。各参数选择分别为σ=1.6,Cont_thr=0.04,Curv_thr=10,R=0.49。
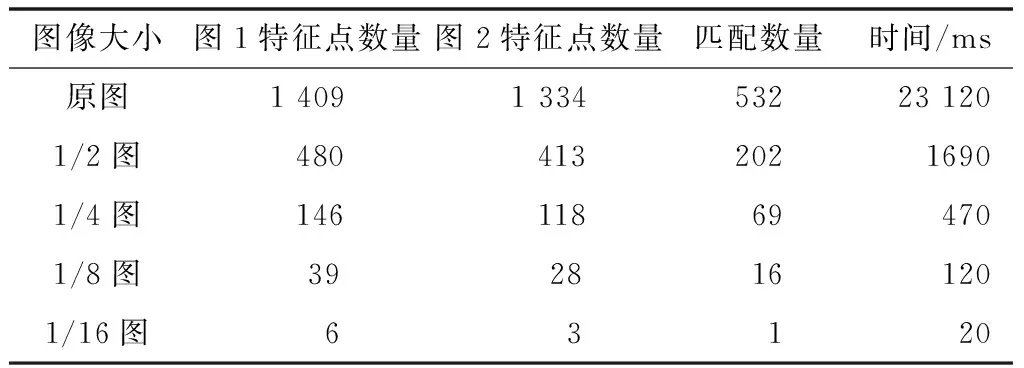
表3 图像大小与特征点以及匹配数量和时间

图7 Miko-lajczyk and Schmid 2005图像库Boat图像
从表3可以看出,图像大小对特征点的数量以及匹配数量和运行时间有很大影响。对于小图像而言,运行时间明显加快。但是如果只依据SIFT算法进行特征点检测和匹配,当图像大小在100×100左右时,检测出来的特征点将非常少。图7是对同一个物体不同角度进行拍摄识别,如果不是同一个物体而是同一类物体,比如铁路扣件图像,其特征匹配数量将更加少,从而影响正确识别扣件状态。
3 去光照变化及添加位置的扣件图像分类
3.1 去光照影响
在SIFT算法中,光照条件对特征点的检测和匹配产生很大的影响。虽然对128维向量采用归一化方法消除了线性光照的影响,但是在实际应用中,很多复杂环境的光照条件并不一定满足线性光照的条件。尤其是对于物体识别而言,由于我们识别的时候,很多时候并不是同一个物体,而是同一类物体。图8为在不同的天气环境下采集的铁路扣件图像。为了识别扣件的状态,包括正常、断裂、缺失等状态。图像采集的并不是同一个扣件,通过轨道检测车在线路上运行,采集的是轨道上所有的扣件图像,扣件图像大小180×120,由于所有的扣件形状都是类似的,所以可以通过寻找扣件中的特征点来实现扣件状态的识别,对于断裂和缺失的情况,是不能匹配到正常扣件图像的特征点中的。对于正常扣件,在不同天气条件下,光照条件有很大的不同,采集的图像也将有很大的区别。
图8所示的晴天和雨天分别采集的扣件图像。虽然都是同一类扣件,但在不同天气条件下,图像的质量完全不同。如果直接采用SIFT算法进行特征点匹配,则不能够找到匹配点。因此,在此采用先对图像进行增强。然后再检测SIFT点的方法。在本文中,图像增强方法采用直方图规定化方法。
为了实现不同天气的扣件识别,在此以晴天的扣件图像作为标准,通过变换雨天扣件图像的直方图,使其与期望的晴天扣件图像直方图一致。这也是直方图规定化的思想。首先对标准的晴天扣件图像进行直方图均衡化
S=T(r)
(5)
然后对规定的直方图进行均衡化
V=G(z)
(6)
由于都是直方图均衡化,所以,让S=V,则
z=G-1(v)=G-1(T(r))
(7)
得到直方图规定化后的图像,如图9所示。

图9 直方图规定化
图10是晴天和雨天以及晴天和阴天进行扣件匹配的情况,可以看出,经过直方图规定化对扣件直方图进行匹配,然后再进行特征点检测和匹配,可以得到更好的效果。虽然其中也有一些点匹配错误,但是如果加上点的位置信息,则可以很好地识别扣件的状态。图11是原始扣件在不同天气下的图像匹配情况,如果没有经过光照处理,得出来的匹配点几乎是完全错误的,不能正确识别扣件的状态。在自然环境变化的情况下,光照变化并非都是线性光照,因此,采用原始的扣件图像进行匹配的效果不好,如果能够将光照的影响去除掉,则可以得到很好的结果。文中采用直方图规定化方法,通过对直方图进行匹配,能够部分去除非线性光照的影响。如果再加上扣件特征点的位置信息,则可以很好地识别扣件的状态。

图10 直方图规定化后扣件不同天气匹配

图11 原始扣件不同天气匹配
3.2 添加扣件特征点位置信息
从图10和图11可以看出,对原始扣件图像采用SIFT算法几乎无法识别扣件状态。采用光照增强之后,可以实现不同天气下的扣件SIFT特征匹配,但是同样存在一些错误的匹配。在前期的扣件图像提取中,将扣件图像都大致分布在整张图像的中间位置,因此,可以将扣件特征点的位置信息加入到特征点的描述中。从图10来看,正确匹配的特征点在x方向的偏差较小,考虑到扣件图像采集时的位置偏差,因此,定义两个匹配特征点在竖直方向的偏差角度阈值α=30,当两个特征点在竖直方向的连线小于30°时,则认为是匹配的。当运用SIFT特征描述算子确定两个特征点i和j匹配时,再根据式(8)确定角度阈值。
(8)
其中:x1i表示第一幅图第i个特征点的x坐标;x2j表示第二幅图第j个特征点的x坐标;y2j表示第二幅图第j个特征点的y坐标;y1i表示第一幅图i个特征点y坐标;H表示图像高度。如果满足则认为匹配,否则不匹配。图12是添加了位置信息后的匹配结果。可以看出,有了位置信息后,错误的匹配点基本上消除,实现了特征点的正确匹配。

图12 添加位置信息后匹配结果
3.3 实验结果
为了验证算法的有效性,选择大理到丽江的铁路线现场采集的图像作为实验数据。选择晴天、雨天和阴天正常各样本1 000张,选择3种天气下丢失、断裂和遮挡样本各1 000张,将正常样本平均分成2份,每份200张,连续选择5次,计算平均识别率。实验比较了LBP、HOG(梯度直方图)算法和本文算法的分类结果,表4表示的是平均识别率。每次实验选择每种类别图像一张作为训练集,剩下的图像作为测试集,这是一种具有挑战性的实验,在实际中往往会增加训练集的数量。
表4 3种天气下扣件分类结果
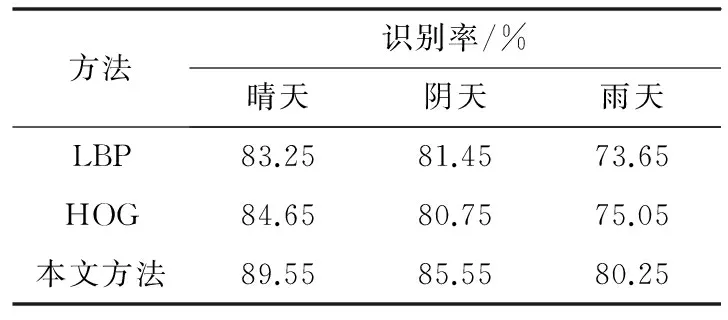
方法识别率/%晴天阴天雨天LBP83.2581.4573.65HOG84.6580.7575.05本文方法89.5585.5580.25
从表4可以看出,采用LBP和HOG方法的识别率比较接近,但是本文方法将识别率提高了大约5%。LBP和HOG是目前比较主流的图像特征表示方法,但是这2种方法对于铁路扣件图像的分类结果,都没有本文方法效果好。
4 结语
SIFT算法在寻找图像特征点方面的适应性比较好,具有抗噪声、旋转不变性、尺度不变性等优点。但是其时间复杂度较高,不适用于实时检测的情形。同时,SIFT算法只对线性光照的改变有适应性,在非线性光照改变条件下检测的效果不是很好。在不考虑时间复杂度的前提下,SIFT算法是比较好的选择。如果用在实时图像识别上,则需要考虑目标识别准确性的前提下,同时考虑算法的时间复杂度。在图像识别方面,很多时候并不需要太多的特征点,只需要几个关键点。这时对于SIFT算法的参数选择至关重要。文中给出了SIFT算法几个关键参数的选择原则,采用RANSAC算法剔除错误的匹配,并给出了R和匹配数量的关系。同时,针对SIFT算法对非线性光照敏感的问题,采用直方图规定化方法,通过匹配标准的扣件直方图,去除了部分光照的影响,针对SIFT算法对小图像特征点比较少的问题,添加了特征点的位置信息,在采集扣件图像时,为了满足识别的实时性要求,通过扣件定位,使得截图的扣件图像尽可能小,这样运算时间也大大减少,成功实现了铁路扣件在不同环境下的识别。
[1]REN J,JIANG X,YUAN J.Noise-resistant local binary pattern with an embedded error-correction mechanism[J].IEEE Transactions on Image Processing,2013,22(10):4049-60.
[2]CHEN D,CAO X,WEN F,et al.Blessing of dimensionality: high-dimensional feature and its efficient compression for face verification[J].2013,9(4):3025-3032.
[3]ZHAO G,AHONEN T,MATAS J,et al.Rotation-invariant image and video description with local binary pattern features[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2012,21(4):1465-1477.
[4]AKHLOUFI M A,BENDADA A.Locally adaptive texture features for multispectral face recognition[C]// IEEE International Conference on Systems Man and Cybernetics.IEEE,2010:3308-3314.
[5]MU Y,YAN S,LIU Y,et al.Discriminative local binary patterns for human detection in personal album[C]// Computer Vision and Pattern Recognition,2008.CVPR 2008.IEEE Conference on.IEEE,2008:1-8.
[6]MORAVEC H P.Rover visual obstacle avoidance[C]// International Joint Conference on Artificial Intelligence.Morgan Kaufmann Publishers Inc.1981:785-790.
[7]HARRIS C.A combined corner and edge detector[J].Proc Alvey Vision Conf,1988,1988(3):147-151.
[8]ROSTEN E,PORTER R,DRUMMOND T.Faster and better: a machine learning approach to corner detection[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2008,32(1):105-119.
[9]CALLONDER M,LEPETIT V,OZUYSAL M,et al.BRIEF: computing a local binary descriptor very fast[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2012,34(7):1281-1298.
[10]RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB: an efficient alternative to SIFT or SURF[C]// International Conference on Computer Vision.IEEE Computer Society,2011:2564-2571.
[11]LEUTENEGGER S,CHLI M,SIEGWART R Y.BRISK: binary robust invariant scalable keypoints[C]// IEEE International Conference on Computer Vision.IEEE,2011:2548-2555.
[12]LOWE D G.Object recognition from local scale-invariant features[C]// The Proceedings of the Seventh IEEE International Conference on Computer Vision.IEEE,2002:1150.
[13]LOWE D G.Distinctive image features from scale-invariant keypoints[M].Kluwer Academic Publishers,2004.
[14]BAY H,TUYTELAARS T,GOOL L V.SURF: Speeded Up Robust Features[J].Computer Vision & Image Understanding,2006,110(3):404-417.
[15]KE Y,SUKTHANKAR R.PCA-SIFT:a more distinctive representation for local image descriptors[C]// IEEE Computer Society Conference on Computer Vision & Pattern Recognition.IEEE Computer Society,2004:506-513.
[16]OJALA T,HARWOOD I.A comparative study of texture measures with classification based on feature distributions[J].Pattern Recognition,1996,29(1):51-59.
[17]OJALA T,PIETIKINEN M,MENPT.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[C]// European Conference on Computer Vision.Springer-Verlag,2000:404-420.
[18]DAVARZANI R,MOZAFFARI S,YAGHMAIE K.Scale- and rotation-invariant texture description with improved local binary pattern features[J].Signal Processing,2015,111:274-293.
[19]GENG C,JIANG X.SIFT features for face recognition[C]// IEEE International Conference on Computer Science and Information Technology.IEEE,2009:598-602.
[20]REN J,JIANG X,YUAN J.Noise-resistant local binary pattern with an embedded error-correction mechanism.[J].IEEE Transactions on Image Processing,2013,22(10):4049-60.
[21]MIKOLAJCZYK K,SCHMID C.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2005,27(10):1615.
[22]TONY L.Scale-space theory: a basic tool for analyzing structures at different scales[J].Journal of Applied Statistics,2011,21(2):224-270.
[23]BOLLES R C,FISCHLER M A.RANSAC-based approach to model fitting and its application to finding cylinders in range data [C]// International Joint Conference on Artificial Intelligence,1981.
Railway Fastener Classfication by Using SIFT Algorithm
WANGQiang1,2
(1.Chengdu Technological University,College of Mechanical Engineering,Chengdu 611730,China;2.Southwest Jiaotong University,School of Mechanical Engineering,Chengdu 610031,China)
Image feature points detection is the important aspect in image research,such as image based object reconstruction,object recognition,moving object tracking,image mosaic and so on.SIFT algorithm,the classic image feature points detecting algorithm,is widely used to solve these visual issues.Matching algorithm based on image feature points is the key to solve many problems and different applications have different requirements.The parameter selection issue of SIFT algorithm is researched.Random sample consensus set algorithm (RANSAC) is combined to eliminate the false matching.The effect of parameters election on match results is analyzed.The relationship of image feature points geneRn with different sizes is studied.In view of the light sensitive of SIFT algorithm,image enhancement is proceeded before matching and the location information is combined.The classification for small fastener images with less feature points is realized.
Scale-invariant feature transform;image classification;parameter selection;location information;feature
10.13542/j.cnki.51-1747/tn.2017.02.001
2017-05-15
四川省教育厅项目(16ZB0330);四川省创新创业项目(201611116007)
王强(1979—),男,副教授,博士研究生,研究方向:计算机视觉、模式识别,电子邮箱:wqiangsky@163.com。
TP391.4
A
2095-5383(2017)02-0001-07

