浅析以立体几何为载体的空间最值问题的求解策略

姜曈

摘要：立体几何是高中数学的重要内容之一，在考试或者练习中常常会遇到，以立体几何为载体的空间最值问题，该问题的解决不仅需要具备识图、用图的能力，更要具备较高的空间想象能力。以立体几何为载体的空间最值问题，常常会找不到着手点，因此文中探究了几种策略，期望能够更好地解决“以立体几何为载体的空间最值问题”。

关键词：立体几何；空间最值；求解策略

近几年，高考和高三模拟考试卷中，经常会遇到“以立体几何为载体的空间最值问题”，该问题要想顺利解决，不仅要有很好的识图能力和用图能力，还要具备较高的立体空间思维能力，更重要的是掌握一些策略。以立体几何为载体的空间最值问题，是当前大部分学生闻之色变的难题，甚至部分学生遇到之后，直接躲过，因为他们根本找不到着手点。

策略1 直观感知，考虑特殊位置

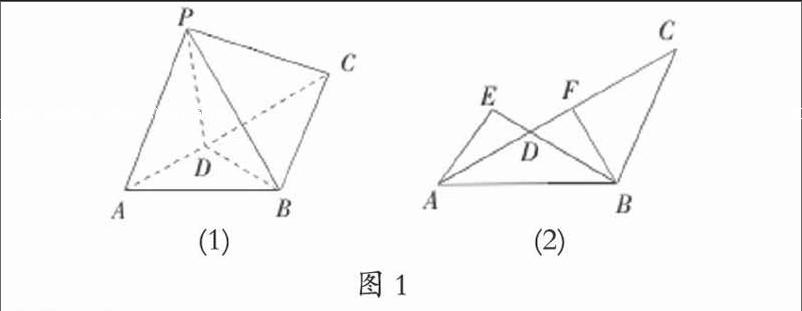
例1 （2016年浙江高考题）如图1（1），在△ABC中，AB= BC=2，∠ABC=1200.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD体积的最大值是 。

【分析】

∵PD=DA，PB=BA

∴该题可以转化为△ABC以BD为轴进行折叠，折叠过程中形成的三棱锥P-BCD的体积何时最大？

直观感知，平面PBD⊥平面BCD时，三棱锥P-BCD的体积将取得最大值。

解（略）

【评注】 例题1的关键就是要能够灵活运用“PD=DA，PB=BA”这一已知条件，完成该条件的转化，将问题转化为“折叠”问题。“折叠”问题是较为容易，且直观的问题，只能够转化成为“折叠”问题，后面的问题即可迎刃而解。

策略2 立体图形问题转化成为不等式问题

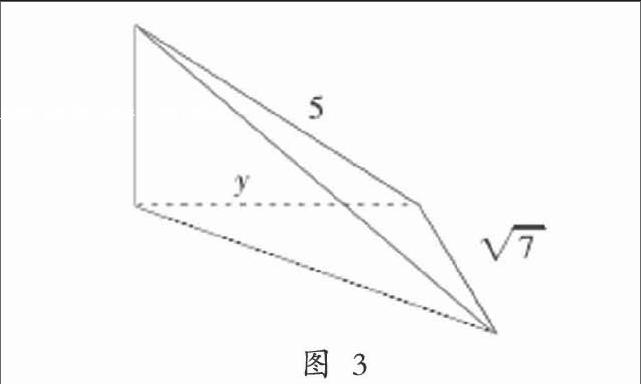
例2 图2 展示了某一个几何图形的三视图，当x与y均为最大值时，该立体几何的体积为

【分析】 正视图、俯视图以及侧视图均为三角形，可以得知该几何图形为三棱锥。通过图2可以将三棱锥的平面图画出，如（图3）。均值不等值用以求最值的关键就是要构造不等关系，该题目中就要利用图3的平面图，联系三棱锥的体积公式V=（1/3）S×H（S是底面积，H是三棱锥的高）。

解（略）

【评注】 根据三视图画出立体几何的平面图，这不是件难事，但是解决本题的关键就是构造不等式关系。在立体几何中构建不等式关系时，运用频率最高的不等式关系就是：a2+b2≥2ab，该不等式关系主要来源于勾股定理：a2+b2=c2。

策略3 立体图形问题转化为函数问题

例3 三棱柱ABC-A1B2C3（如圖4）中，AA1⊥BC，A1B⊥BB1.

（1）求证：A1C⊥CC1

（2）若AB=2， AC=√3 ，BC=√7，问AA1为何值时，三棱柱ABC-A1B2C3体积最大，并求三棱柱

ABC-A1B2C3体积的最大值。

【分析】 该题目解决时，可以将AA1作为自变量x，建立一个有关三棱柱体积的函数关系，然后在利用函数的性质，即可求得最大值。

解（略）

【评注】 利用函数的性质解决词类单变量最值问题，是最常用的方法，更是通性通法。以立体几何为依托考察函数最值的求法，既能够增加问题的神秘感，迷惑学生，还能够丰富试题的知识内涵，巧妙地回避了简单直白的命题方式。

立体几何为载体的空间向量最值问题，确实是当前的难点，而将几何问题转化成为函数问题、不等式问题就能够有效地的解决，另外还可以通过直观感觉，进行解决。

参考文献：

[1] 朱长改，徐加生.立体几何最值问题的求解策略[J].中学生数理化（高考版）.2010（03）endprint