增压柴油机气道流量系数评价与稳流特性研究

刘福水 康 宁 徐 洋 黎一锴

(1.北京理工大学机械与车辆学院， 北京 100081； 2.北京理工大学北京电动车辆协同创新中心， 北京 100081)

增压柴油机气道流量系数评价与稳流特性研究

刘福水1,2康 宁1徐 洋1黎一锴1

(1.北京理工大学机械与车辆学院， 北京 100081； 2.北京理工大学北京电动车辆协同创新中心， 北京 100081)

理论推导了增压柴油机考虑气体可压缩性的流量系数计算公式，建立了直气道稳态流动仿真模型，研究了进气压力与气道压差对直气道稳流特性的影响。结果表明：当气体可压缩性较强时，Ricardo评价公式的计算结果偏离真值的程度越大，不适用于增压气道性能的评价，理论推导的流量系数计算公式能够适用于增压气道流通能力的评价计算；可压缩性对气体流动的影响与进气压力无关；与相对压差r有关，随着r的增加，可压缩性对气体流动的影响逐渐增强；当r一定时，随着进气压力的增大，平均流量系数Caver逐渐增大，增大幅度逐渐减小；当进气压力一定时，随r的增大，Caver先增加后减小；rmax随着进气压力的增加近似呈线性递减。

增压柴油机； 可压缩性； 评价公式； 稳流特性

引言

在节能减排的国际大背景下，柴油机正朝着高增压、高喷油压力的方向发展[1-4]。越来越高的喷油压力使油束雾化的质量越来越好，配合采用增压技术，在相同排量的情况下，可以增大喷油量，提高功率密度。而对于高功率密度柴油机来说，循环进气量是制约功率提高的主要因素之一，所以其进排气系统的设计就显得尤其重要。

气道性能直接影响进排气系统的性能。利用稳流试验方法评定和预测气道的流通特性及气流运动强度，已成为内燃机研究的重要手段之一[5-7]。目前，国际上广泛使用的气道评价方法[8]主要有英国Ricardo方法、德国FEV方法、奥地利AVL方法以及美国SwRI方法；LIU等[9]也提出了SKLE评价方法。以上评价方法大多是在不可压缩流体的假设条件下提出的，而在大压差条件下，气体的可压缩性不能够忽略，因此传统的评价方法对增压状态下的气道性能评价存在一定的局限性[10]。国内学者对此问题进行了一些研究[11-14]。在增压状态下，气道内气流运动的相关研究仍然较少。但是，随着增压技术的应用越来越广泛，探明增压条件下气道内气流运动特性显得很重要。

本文考虑气体的可压缩性，理论推导流量系数的计算公式，建立自然吸气、增压气道稳态流动仿真计算模型，研究自然吸气与增压条件下进气压力与气道压差对直气道稳流特性的影响规律。

1 理论依据与公式推导

压差是气体在流道中流速改变的根本原因，几何条件是使气流可逆加速的外部条件，在压力条件得到满足的前提下，几何条件是决定性的[15]。实际情况下，在气道进出口压差一定的条件下，气道的几何形状很难也不可能与理想形状一样(由于摩擦作用以及加工凹台和气门的存在)，从而导致了流量损失。流量系数为实际流量与理论流量的比值，当考虑气体可压缩性时，公式中的流量应为质量流量。其中，实际流量由流量计等测量仪器测量计算得到；理论流量由理论推导得出。

1.1 理论质量流量公式推导

假设气道形状为理想形状时，气体流经气道过程中没有沿程阻力和局部阻力损失，即没有摩擦、加工凹台、气门等影响，该过程为可逆绝热过程[16]，此时气道的质量流量应该为理想状态下的最大质量流量，即理论质量流量。

基于以上假设，当气道进口和出口的绝对压力都保持不变且进出口有一定压力差时，将气道内的气流运动看作稳定流动，则单位质量流经开口系统时的稳定流动能量方程有

(1)

式中q——单位质量工质与外界交换的热量，J/kgh1——进口比焓，J/kgh2——出口比焓，J/kgv1——进口气流速度，m/sv2——出口气流速度，m/sz1——进口高度，mz2——出口高度，mg——重力加速度，m/s2wnet——与外界交换的净功，J/kg

通常，气道进出口位置改变不大，所以位能项g(z2-z1)可以忽略不计。气体在气道的流动过程中不对外做功，wnet=0，假设为可逆绝热过程，q=0。则式(1)可简化为

(2)

式中h0——滞止焓

当气体流动为亚音速流时，流道出口截面的截面积最小、速度最大，通常计算流经此截面的质量流量来代表气流的质量流量。对于气道来说，以流经气门座圈最小截面处的质量流量进行计算。

使用下标1代表气门座圈最小截面状态，由式(2)可得该截面上的平均速度v1为

(3)

式中cp——定压比热容T0——滞止温度

等熵过程方程和气体状态方程分别为

(4)

(5)

式中k——绝热指数R——气体常数ρ——气体密度p——气体压力

(6)

式中p0——滞止压力ρ0——滞止密度

气门座圈最小截面处气体密度为

(7)

则流经气道的理论质量流量qth可表示为

qth=ρ1A1v1=

(8)

式中dv——气门座圈最小截面直径，m

1.2 实际质量流量公式推导

当考虑气体的可压缩性时，流量计测得的实际流量需要进行可压缩性修正。本文以孔板流量计为例进行可压缩性修正。

因为摩擦和节流损失的作用，所以流体流经孔板的过程为不可逆绝热过程。为方便计算，先假设此过程为可逆绝热过程，换热量q=0，对外净功wnet=0，孔板流量计水平安装，则有

(9)

(10)

式中下标3和4分别代表孔板上、下游截面。

则式(9)可表示为

(11)

质量守恒方程为

ρ3A3v3=ρ4A4v4

(12)

将式(4)、(12)代入式(11)中可以得到

(13)

则可以求出流经孔板流量计的理想质量流量

(14)

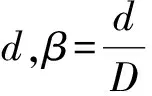
(15)

则实际质量流量qac为

qac=Cqm

(16)

式中，C为孔板流量计的流出系数，考虑了摩擦和节流损失的作用，可以通过流量计的标定确定。

由式(8)、(15)、(16)可得考虑气体可压缩性流量系数

(17)

(18)

2 试验系统与方法

试验系统示意图见图1，主要包括稳流气道试验台和进气增压系统。稳流气道试验台由天津大学内燃机燃烧学国家重点实验室研制，主要包括：试验台主体、气缸、叶片风速仪、安装管道、孔板流量计、稳压箱、风机、变频器、数据采集仪及计算机系统等。进气增压系统包括：空气压缩机、球阀、进气稳压箱、温度和压力传感器等。试验用缸盖为某增压型柴油机缸盖，其中气道类型为直气道，缸径132 mm，最大气门升程11 mm，主要测试设备的技术参数见表1。

图1 试验系统示意图与实物图Fig.1 Experiment system diagram and photo1.进气压力传感器 2.叶片风速仪传感器 3.气缸压力传感器4.进气温度传感器 5.孔板前压力传感器 6.孔板后压力传感器 7.风机 8.空气压缩机 9.阀A 10.阀B 11.进气稳压箱12.缸盖 13.气缸 14.孔板 15.阀C 16.阀D 17.变频器 18.工作台

设备 关键参数空气压缩机型号HN⁃16/8，排气量16m3/min，排出压力08MPa孔板流量计测量范围0～1500Pa，精度±075%压力传感器型号3804，量程±10kPa、0～400kPa大气压力传感器型号JQYB⁃A1，量程0～110kPa温度传感器型号Pt100，量程0～45℃

进行自然吸气试验时，需把图1中的增压进气系统拆卸，关闭阀C、打开阀D，此时气道进口状态为环境大气，在计算机软件中设置一定压差，变频器则自动调节风机的转速，使大气压力与压力传感器3的差值达到目标压差，稳定一段时间后即可采集数据。

进行进气增压试验时，仪器和设备按图1所示安装，关闭阀D、打开阀C，通过调节阀A、B、C的开度来控制进气稳压箱以及气缸内的气体压力，各位置压力达到目标要求且稳定一段时间后采集数据。

3 稳流气道仿真计算模型

3.1 模型的建立与设置

采用AVL FIRE软件进行稳流气道仿真计算，该商业软件已被广泛应用于流体的CFD计算[17-19]。取试验系统一部分建立几何模型，见图2，包括稳压箱(370 mm×210 mm×170 mm)、气道、气门、气门座圈、气缸(长度330 mm)。气道气流运动为三维可压缩黏性流动，边界条件：进口设总压，出口设静压，具体数值参照试验实际状态和仿真计算方案，湍流模型选k-ε湍流模型；采用Simple方法进行离散，动量方程采用MINMOD Relaxed格式，连续性方程和湍流方程采用中心差分格式，能量方程采用迎风格式进行求解。

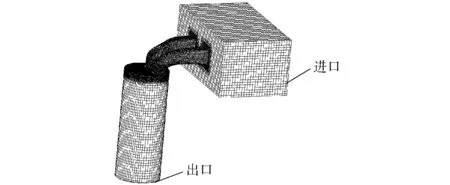
图2 几何模型Fig.2 Geometric model

湍流模型的初始湍流强度和湍流混合尺度[20]为

(19)

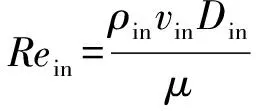
式中Re——雷诺数Din——气道入口当量直径μ——动力粘度I——湍流初始强度L——湍流混合尺度

下标in代表气道入口状态。

3.2 模型的校核与验证

以花费尽可能小的计算成本获得尽可能精确的计算结果为目的，对仿真模型分别进行了网格尺寸和收敛标准的校核，以及试验验证。

3.2.1 网格尺寸校核

由于不同气道位置的速度梯度不同，所以采用局部网格尺寸不同的划分方案进行校核，方案见表2。固定气门升程10 mm，边界条件为：进口总压100.18 kPa，出口静压96.7 kPa，即压差为3.48 kPa；收敛标准取0.001。

表2 网格划分方案

经计算可知，随着网格数逐渐增大，即网格尺寸逐渐减小，实际流量收敛于某一值，计算时间呈指数增长。其中，方案4计算结果与收敛值偏差很小且计算时间适中，所以选用方案4进行后续计算。

3.2.2 收敛标准校核

校核方案为：采用3.2.1节的边界条件，网格划分采用方案4，收敛标准分别取0.1、0.01、0.001、0.000 1进行计算。经计算，收敛标准0.001与0.000 1的相对误差仅为0.45%，但是收敛标准0.000 1的计算时间却是0.001的6倍多，所以收敛标准选取0.001。

3.2.3 试验验证

为验证仿真模型的准确性，采用上述方法对不同气门升程2～11 mm进行建模计算，并与试验结果进行比较，仿真和试验的边界条件相一致，其中自然吸气的边界条件为：进口总压100 kPa，压差为4 kPa；进气增压边界条件为：进口总压约150 kPa，压差约50 kPa，对比结果见图3。

从图3可知，各气门升程下的仿真计算结果与试验值基本重合，仿真结果略大于试验结果，可能是因为：仿真模型是对试验系统的简化，且没有考虑壁面粗糙度的影响；试验的压力测点与模型边界条件的位置稍有差别。经计算，在自然吸气与增压条件下，平均流量系数的仿真与试验结果的相对误差分别为4.2%、4.8%，说明建立的数值模型是可靠的、准确的，能够代替试验进行研究。

4 结果与分析

为研究进气压力与气道压差对直气道稳流特性的影响规律，仿真计算方案见表3。

图3 模型验证结果Fig.3 Results of model validation

进气压力/kPa气道压差/kPa1004、6、8、10、125、15、20、30、403004、10、15、20、25、30、40、60、80、1005004、10、20、30、40、60、80、100

注：每个压差下气门升程变化范围：2～11 mm，间隔1 mm。

定义Cf、CRf分别为由推导公式和Ricardo公式计算得到的流量系数；Caver、CRaver分别为对应Cf、CRf的平均流量系数，是由各个气门升程得到的流量系数曲线下的积分面积与积分区间的比值得来。

4.1 评价公式对比

图4为自然吸气条件即进气压力为100 kPa时，CRf和Cf随气门升程和压差的变化曲线。由图4a可知，随着压差的增加，每个升程下的CRf均出现一定程度的降低，且随着升程的变大，CRf降低的幅度越大。在气门升程为11 mm时，压差从4 kPa增加到40 kPa，CRf降低了约22.6%。而由图4b可知，随着压差的增加，在各气门升程下的Cf基本保持不变。

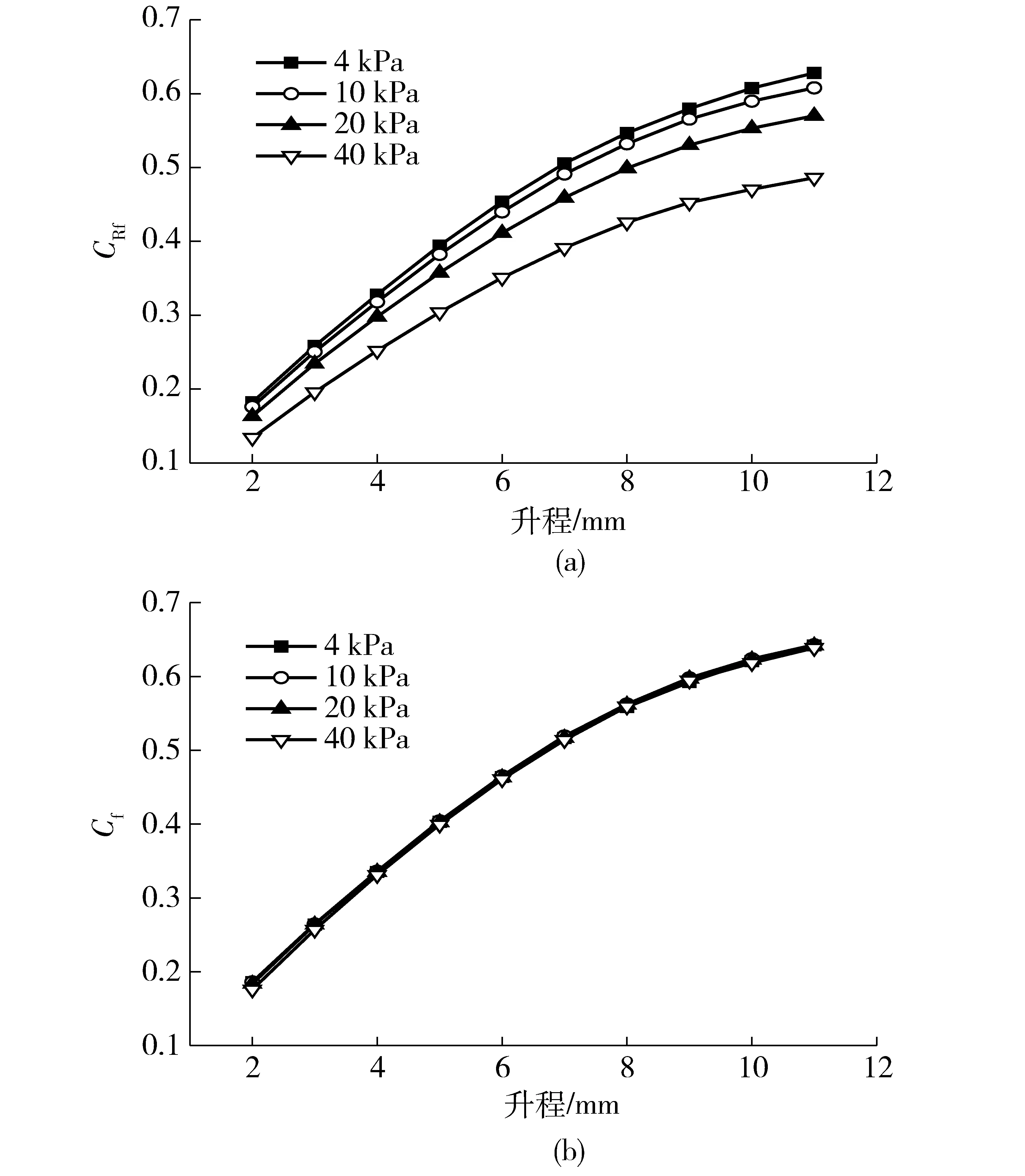
图4 自然吸气条件下CRf与Cf的变化曲线Fig.4 Changing curve of CRf and Cf under naturally aspirated condition

图5为不同进气压力下，Caver、CRaver随压差的变化曲线。从图5可以看出，当进气压力一定时，随着压差的增加，CRaver逐渐降低，且降低的幅度也十分明显，当进气压力为300 kPa时，压差从4 kPa增加到100 kPa，CRaver降低了约20.5%；而Caver基本保持不变。当气道压差一定时，随着进气压力的增加，Caver、CRaver均逐渐增加；各气道压差下Caver与CRaver两者之间的差值随着进气压力的增加不断降低。

图5 不同进气压力下Caver、CRaver的变化曲线Fig.5 Changing curve of Caver and CRaver under different intake pressures

图6 气门升程11 mm下的速度场Fig.6 Velocity fields of valve lift of 11 mm

此外，2种方法计算得到的流量系数之间的差值在一定程度上也反映了可压缩性对气道内气体流动的影响。由图5可知，当压差一定时，随着进气压力的增加，CRaver降低的幅度反而减弱，可压缩性对气体流动的影响有可能与进气压力有关。为了进一步研究，进行如下数据处理：定义r为气道压差与进气压力的比值，即相对压差；定义δ=(Caver-CRaver)/Caver，即偏差率。

图7为不同进气压力下，δ随r的变化规律。由图7可知，当r一定时，随着进气压力的增加，δ保持不变，说明可压缩性对气体流动的影响与进气压力无关；当进气压力一定时，随着r的增加，δ逐渐增大，即可压缩性对气体流动的影响逐渐增强。

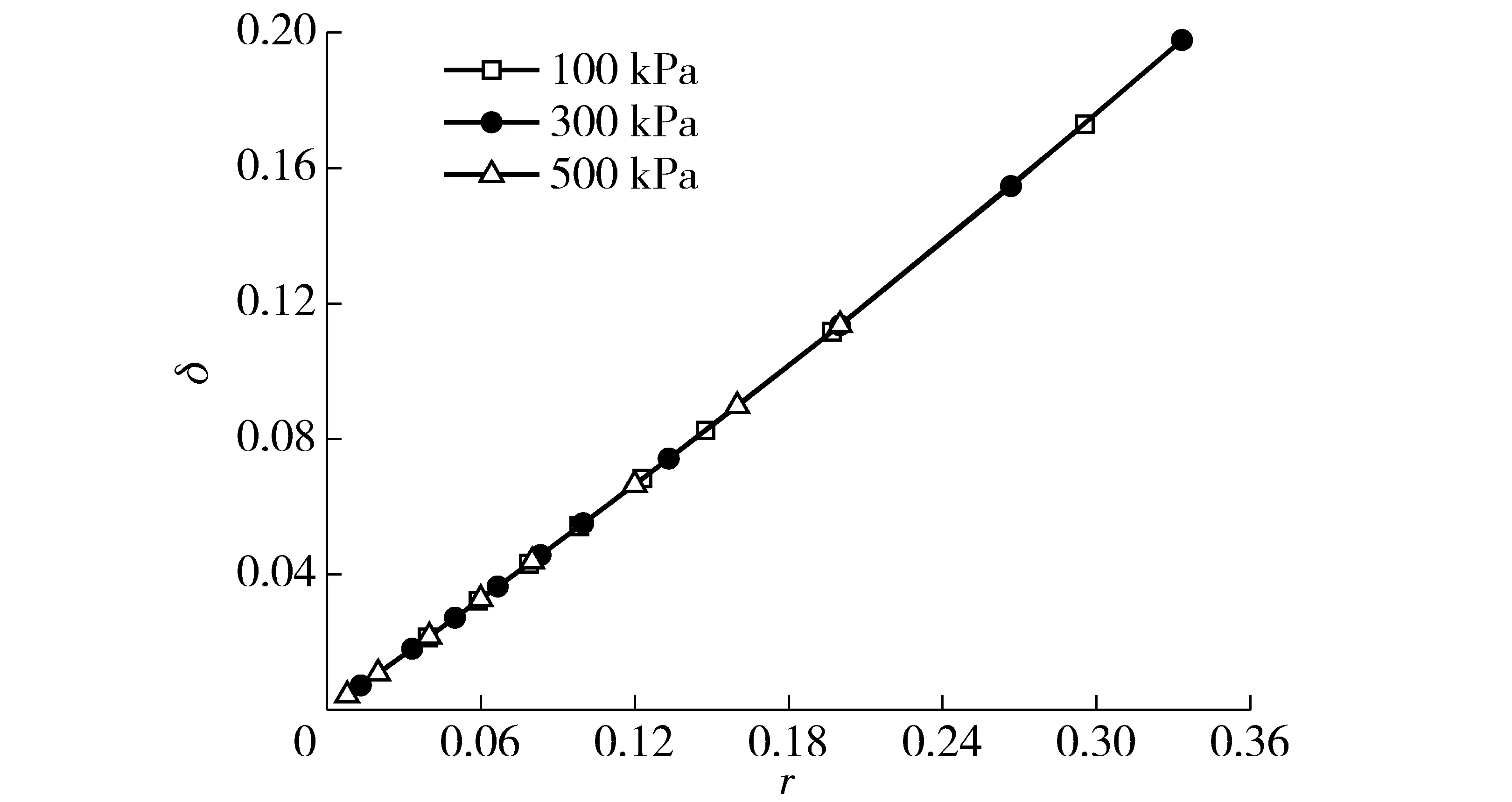
图7 不同进气压力下δ随r的变化曲线Fig.7 Changing curve of δ with r under different intake pressures

4.2 直气道稳流特性

如图8所示，将模型分为2个区域，定义截面1-1与2-2所包围的区域为喉口段，剩余区域为进出口段，截面3-3为平均马赫数Ma测量面。取气门升程为11 mm时的计算结果进行分析。

图8 截面分布示意图Fig.8 Sections distribution diagram

图9 Ma随进气压力与r的变化曲线Fig.9 Changing curve of Ma with r under different intake pressures

图9为不同进气压力下气门座圈最小截面上的Ma随r的变化规律。由图9可知，当进气压力一定时，随着r增加，Ma不断增大，但增大趋势逐渐变缓；当r一定时，随着进气压力增加，Ma逐渐增大，但变化范围很小，相同r下进气压力为300 kPa与500 kPa的Ma几乎相同。

图10为不同进气压力下，喉口段总压损失所占总体总压损失的百分比随r的变化曲线。从图10可知，当进气压力一定时，随着r的增加，喉口段总压损失所占比例逐渐增加，且增加幅度逐渐增大；当r一定时，随着进气压力的增加，喉口段总压损失所占比例逐渐降低，且降低的幅度逐渐减小；以r=0.15为界，当r<0.15时，随着进气压力的变化，喉口段总压损失所占比例的变化幅度较大，当r>0.15时，变化幅度较小。

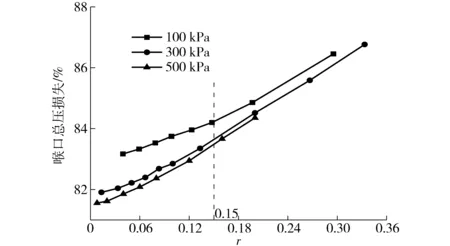
图10 喉口段总压损失Fig.10 Total pressure loss of throat section

图11为不同进气压力下，Caver随r的变化曲线。由图11可知，当进气压力一定时，Caver随r的增加先增大后减小，存在一个峰值。这是因为当r较小时，气体流速较小，粘性边界层较厚，导致气流的有效流通面积减小，当r逐渐增加时，流速增大，有效流通面积变大，所以Caver增加；当流速增大到一定程度时，流动阻力损失所占比重越来越大，从而导致Caver减小。当r一定时，随着进气压力的增加，喉口段总压损失所占比例逐渐减小，所以Caver随进气压力的

增大逐渐增大，但增大的幅度随进气压力的增大逐渐减小，与喉口段总压损失所占比例随进气压力的变化规律一致。

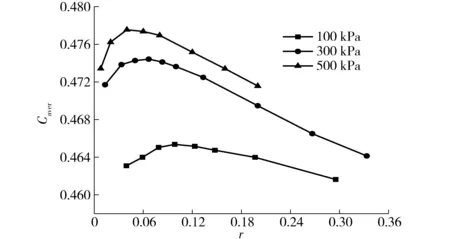
图11 Caver随r的变化曲线Fig.11 Changing curve of Caver with r under different intake pressures

定义rmax为各进气压力下Caver峰值所对应的r值。图12为rmax随进气压力的变化曲线。由图12可知，随着进气压力的增大，rmax逐渐减小，且rmax与进气压力近似呈线性关系。说明随着进气压力的不断增加，获得Caver最大值所需的压差越来越小。

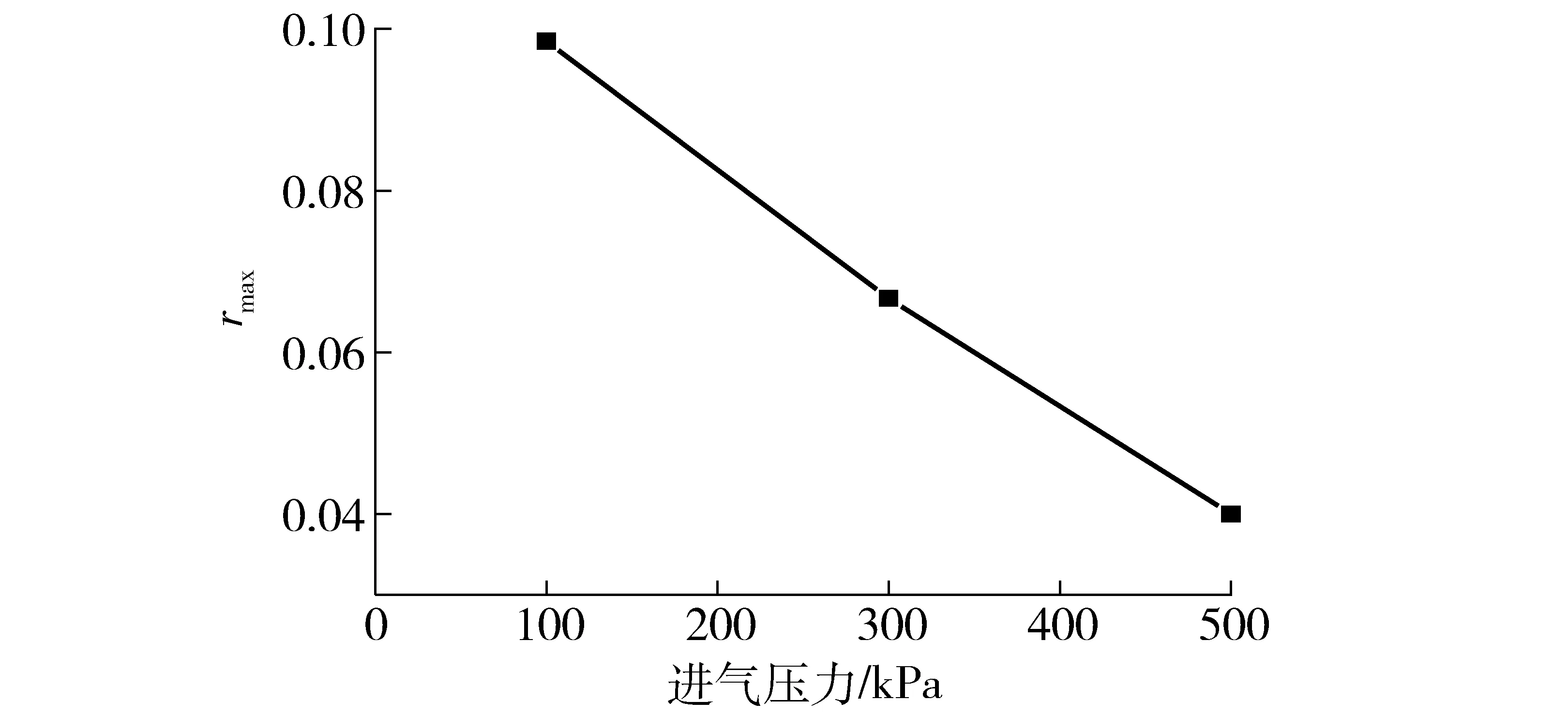
图12 rmax随进气压力的变化曲线Fig.12 Changing curve of rmax with intake pressure

5 结论

(1)随着气道压差的不断增大，气体可压缩性逐渐增强，Ricardo评价公式的计算结果偏离真值的程度越大，不适用于增压气道性能的评价，本文考虑可压缩性推导了流量系数计算公式。

(2)可压缩性对气体流动的影响与进气压力无关；与相对压差r有关，随着r的增加，可压缩性对气体流动的影响逐渐增强。

(3)当r一定时，随着进气压力的增大，Caver逐渐增大，增大幅度逐渐减小；当进气压力一定时，随着r的增大，Caver先增加后减小；rmax随着进气压力的增加逐渐减小，且近似呈线性关系。

1 郑尊清，张文强，尧命发，等. 高/低压EGR对两级增压柴油机性能和排放影响的试验研究[J]. 内燃机工程, 2014, 35(1): 1-7. ZHENG Zunqing, ZHANG Wenqiang, YAO Mingfa, et al. Effect of high/low pressure EGR on combustion and emissions of two-stage turbocharged diesel engine[J]. Chinese Internal Combustion Engine Engineering, 2014, 35(1): 1-7.(in Chinese)

2 刘博，胡志龙，李华雷，等. 可调二级增压柴油机旁通阀特性和调节规律的试验[J]. 内燃机学报, 2012, 30(1): 72-78. LIU Bo, HU Zhilong, LI Hualei, et al. Experiment on characteristic of bypass valves and regulating MAP of a regulated two-stage turbocharged diesel engine[J]. Transactions of CSICE, 2012, 30(1): 72-78.(in Chinese)

3 PARLAK A, YASAR H, SOYHAN H S, et al. Optimization of an irreversible diesel cycle: experimental results of a ceramic coated indirect-injection supercharged diesel engine[J]. Energy & Fuels, 2008, 22(3): 1930-1935.

4 JAYASHANKARA B, GANESAN V. Effect of fuel injection timing and intake pressure on the performance of a DI diesel engine—a parametric study using CFD[J]. Energy Conversion and Management, 2010, 51(10): 1835-1848.

5 刘瑞林，刘志刚，刘伍权，等. 4气门发动机单气门工作时缸内滚流运动的稳态测量研究[J]. 内燃机学报, 2001, 19(5): 405-409. LIU Ruilin, LIU Zhigang, LIU Wuquan, et al.Studies on steady measurement of in-cylinder tumble in a 4-valve engine with one inlet valve opening[J]. Transactions of CSICE, 2001, 19(5): 405-409.(in Chinese)

6 刘瑞林，关立哲，刘志刚，等. 4气门汽油机缸内涡流的稳态测量研究[J]. 内燃机学报, 2001, 19(4): 377-382. LIU Ruilin, GUAN Lizhe, LIU Zhigang, et al. Studies on steady measurements of in-cylinder swirl in a 4-valve gasoline engine[J]. Transactions of CSICE, 2001, 19(4): 377-382.(in Chinese)

7 王天友，林荣文，刘书亮，等. 直喷式柴油机进气道变压差稳流试验方法的研究[J]. 内燃机学报, 2005, 23(2): 131-136. WANG Tianyou, LIN Rongwen, LIU Shuliang, et al. Study on steady flow test method for inlet port of DI diesel engines with variable pressure drop[J]. Transactions of CSICE, 2005, 23(2): 131-136.(in Chinese)

8 段家修，尧命发，许振忠. 柴油机进气道性能试验与评价方法[J]. 汽车技术, 2001(7): 23-25.

9 LIU S L, LI Y F, LU M. Prediction of tumble speed in the cylinder of the 4-valve spark ignition engines[C]. SAE Paper 2000-01-0247, 2000.

10 ALGIERI A, BOVA S, DE BARTOLO C. Influence of valve lift and throttle angle on intake flow in a high-performance four-stroke motorcycle engine[J]. ASME Journal of Engineering for Gas Turbines and Power, 2006, 128(4): 934-941.

11 陈涛，诸葛伟林，张扬军，等. 高压差下增压柴油机进气道流通特性研究[J]. 内燃机工程, 2008, 29(5): 57-61. CHEN Tao, ZHUGE Weilin, ZHANG Yangjun, et al.Research on flowability in intake port of turbocharged diesel engine at high port pressure drop[J]. Chinese Internal Combustion Engine Engineering, 2008, 29(5): 57-61.(in Chinese)

12 祖炳锋，王振，徐玉梁，等. 增压状态下汽油机进气道性能评价及流通特性分析[J]. 天津大学学报：自然科学与工程技术版, 2012, 45(10): 865-869. ZU Bingfeng, WANG Zhen, XU Yuliang, et al.Intake port performance evaluation and flow characteristic analysis of gasoline engine under boosted condition[J]. Journal of Tianjin University: Science and Technology, 2012, 45(10): 865-869.(in Chinese)

13 YU C H, LI X R, WANG X Y, et al. Research on characteristics of intake flow under supercharging condition in diesel engine[C]∥2011 International Conference on Electric Information and Control Engineering, 2011:5237-5240.

14 LI X R, ZHAO L M, LIU F S, et al. Study on characteristics of intake port on supercharged diesel engine[C]∥2012 International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, 2012: 659-662.

15 童钧耕，蒋智敏，沈维道. 工程热力学[M]. 3版. 北京: 高等教育出版社, 2006: 232-239.

16 ANNAND W J, ROE G E. Gas flow in the internal combustion engine[M]. Sparkford: G. T. Foulis & Co. Ltd., 1974.

17 雷基林，覃忠耿，贾德文，等. 柴油机螺旋气道数字化设计方法[J/OL]. 农业机械学报, 2015, 46(9): 343-349. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150950&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.09.050. LEI Jilin, QIN Zhonggeng, JIA Dewen, et al.Digital design method of helical intake port for diesel engine[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 343-349. (in Chinese)

18 段炼, 袁寿其, 胡林峰,等. 高压共轨喷油器控制阀空化研究[J/OL]. 农业机械学报, 2015, 46(5): 321-327. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150545&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.05.045. DUAN Lian, YUAN Shouqi, HU Linfeng, et al.Cavitation analysis of control-valve in high-pressure common rail injector[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 321-327. (in Chinese)

19 刘琦, 欧阳光耀, 杨昆,等. 高压喷射条件下非常态燃油喷嘴内部空化流动特性[J/OL]. 农业机械学报, 2016, 47(6): 333-339.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160644&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.06.044. LIU Qi, OUYANG Guangyao, YANG Kun, et al.Nozzle inner cavitation flow characteristics of non-normal fuel based on high pressure injection condition[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 333-339. (in Chinese)

20 LU Z, WANG T Y, LI X C, et al. Parametric design of the tangential intake port in diesel engines[J]. Proc. IMech E. Part D: Journal of Automobile Engineering, 2013, 227(3): 409-421.

Discharge Coefficient Evaluation and Steady Flow Characteristics for Intake Port of Turbocharged Diesel Engine

LIU Fushui1,2KANG Ning1XU Yang1LI Yikai1

(1.SchoolofMechanicalEngineering，BeijingInstituteofTechnology，Beijing100081，China2.CollaborativeInnovationCenterforElectricVehicles，BeijingInstituteofTechnology，Beijing100081,China)

For a turbocharged diesel engine, the differential pressure in the intake port is up to 60～80 kPa during the intake stroke, and the gas compressibility needs to be considered. Therefore, a formula of the discharge coefficient with consideration of the gas compressibility was theoretically derived and compared with the Ricardo’s formula. Furthermore, the steady flow simulation models of the direct intake port were established, and the effects of intake pressure and differential pressure on steady flow characteristics were studied. Results showed that when the compressibility of gas in the intake port became stronger, the calculation values of Ricardo’s formula were deviated from the true value much more, so the Ricardo’s formula cannot be used for the performance evaluation of the intake port in turbocharged diesel engines any more. However, the derived formula can be still applied to the flow capacity evaluation calculation. From the investigation of the steady flow characteristics, the influence of the compressibility on the air motion was irrelevant to the intake pressure, but it was relevant tor(differential pressure divided by the intake pressure), and with the increase ofr, the influence was enhanced. Whenrwas the same, with the increase of intake pressure,Caver(mean discharge coefficient) was increased. When intake pressure was the same, with the increase ofr,Caverwas firstly increased and then decreased. Thus under each intake pressure, with the variation ofr, there was a peak, and the correspondingrwas calledrmax. With the increase of intake pressure,rmaxwas approximately decreased linearly.

turbocharged diesel engine； compressibility； evaluation formula； steady flow characteristics

10.6041/j.issn.1000-1298.2017.06.045

2016-11-29

2016-12-29

基础产品创新计划科研项目(0410)

刘福水(1964—)，男，教授，博士生导师，主要从事内燃机流动与燃烧研究，E-mail： fushui_liu@bit.edu.cn

TK421+.8

A

1000-1298(2017)06-0341-08