土壤耕作部件极窄刀齿与土壤作用关系研究

尤 泳 贺长彬 王德成，2 王光辉

(1.中国农业大学工学院， 北京 100083； 2.中国农业大学农业部土壤-机器-植物系统技术重点实验室， 北京 100083)

土壤耕作部件极窄刀齿与土壤作用关系研究

尤 泳1贺长彬1王德成1，2王光辉1

(1.中国农业大学工学院， 北京 100083； 2.中国农业大学农业部土壤-机器-植物系统技术重点实验室， 北京 100083)

随着保护性耕作技术和低扰动土壤处理技术的发展，新型土壤耕作部件越来越多地采用窄类或极窄类刀齿形式。通过理论分析和室内土槽试验，对矩形齿和三角形齿两种极窄刀齿贯入土壤造成的土壤失效机理、刀齿工作时的主要阻力来源、刀齿形状尺寸参数对贯入阻力的影响以及刀齿贯入阻力预测模型进行了研究。结果发现，极窄刀齿在贯入土壤过程中，土壤与刀齿相互作用产生应力场和速度场，土壤主要受到刀齿的挤压而失效；刀齿所受阻力可以通过相互作用过程中产生的力学分量进行预测，特别是该预测模型能够较好地反映刀齿在不同深度下所受阻力的变化趋势，研究还发现在土壤参数一定的情况下，极窄刀齿所受阻力与刀齿和土壤的接触面积直接相关，极窄刀齿的形状尺寸参数是其受力的重要影响因素。

土壤耕作部件； 极窄刀齿； 土壤失效机理； 预测模型； 相互作用关系

引言

随着保护性耕作技术和低扰动土壤处理技术的发展，新型机具如打孔透气机械、切根机和肥料注射机械等开始得到应用，作业部件开始向矩形齿、三角形齿、无正切刃旋耕刀、月牙形弯刀等刀齿类耕作部件扩展，这些刀齿类耕作部件因其工作厚度远小于耕作深度，属于窄齿类工作部件[1]。与传统耕作部件(如铧式犁、松土铲、开沟器等)相比，这种窄齿类工作部件作业时，不会产生大面积的土壤失效，对土壤的扰动相对较低[2-7]，刀具结构尺寸对作业效果影响较大，这类结构的设计和优化需要刀齿-土壤之间的相互作用关系作为支撑。现有的刀齿-土壤相互作用关系的研究中，大多将传统的耕作部件作为主要形式，同时认为土壤失效的假设符合库仑定律[8]，其目的在于通过研究耕作部件的结构参数、作业参数以及土壤条件参数对耕作部件受力、土壤扰动程度、失效形式等方面的影响，探索刀齿-土壤相互作用关系规律，为设计和优化土壤耕作关键部件和选择作业参数提供理论依据[9-17]。围绕上述内容，相关学者开展了大量的理论分析、数字化虚拟仿真分析、室内土槽试验和田间试验[18-23]，但这些基于传统耕作部件形式开展的土壤-机具相互作用关系研究往往将耕作部件简化为平板类的宽刀齿[1，21，24]，导致刀具结构尺寸参数被忽略，其研究结果无法指导极窄刀齿的设计和优化。本文以矩形刀齿和三角形刀齿为例，对以贯入形式为主的极窄刀齿(以下简称刀齿)造成的土壤失效机理进行分析，提出刀齿贯入阻力预测模型，并通过土槽试验对刀齿贯入阻力预测模型进行验证与修正，研究刀齿结构尺寸参数对刀齿受力的影响，为极窄刀齿类耕作部件的设计与优化提供理论支撑。

1 刀齿贯入阻力模型假设

1.1 试验用刀齿类型与尺寸

参考打孔透气机械、切根机和肥料注射机械等用于贯入土壤的刀具类型和尺寸，设计矩形刀齿和三角形刀齿用来分析极窄刀齿所造成的土壤失效，并进行试验。2种刀齿的厚度均为7 mm，刀齿均开有刃角(30°)，刀齿最大宽度为90 mm，最大高度为207 mm，有效工作深度为160 mm，其中三角形刀齿刃口与竖直方向的夹角也为30°。矩形刀齿和三角形刀齿均开有3个等距且直径相同的通孔，用于安装和固定。矩形刀齿和三角形刀齿实物图和结构示意图如图1所示。

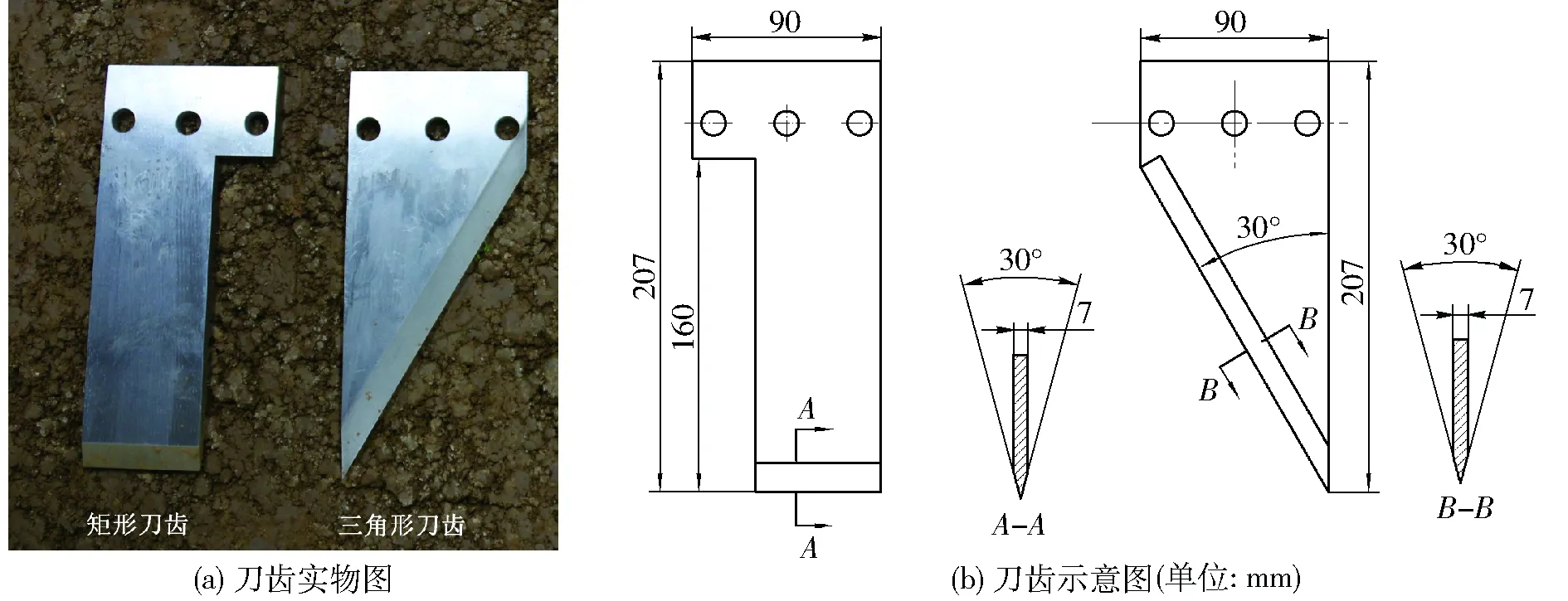
图1 矩形刀齿和三角形刀齿Fig.1 Rectangle tine and triangle tine

1.2 土壤失效机理分析

试验所用土壤，砂粒含量(质量分数)为44.6%，粉粒含量为35%，粘粒含量为20.4%，主要用来观察土壤失效和进行土槽试验。为便于观察极窄刀齿在贯入土壤过程中土壤颗粒的运动情况和土壤变形，采用透明有机玻璃盒作为盛装土壤的容器。土壤经筛分(孔径为2 mm)后装入玻璃盒(长×宽×高为500 mm×250 mm×250 mm)，并将表层轻轻压实，将矩形刀齿匀速地贯入到土壤中，贯入时保持刀齿垂直运动，观察刀齿在贯入土壤时土壤的变形趋势及土壤颗粒运动情况，完全贯入后拍摄照片并对土壤变形进行图像处理。刀齿与土壤的接触情况以及刀齿在贯入土壤后造成的土壤失效情况如图2所示。

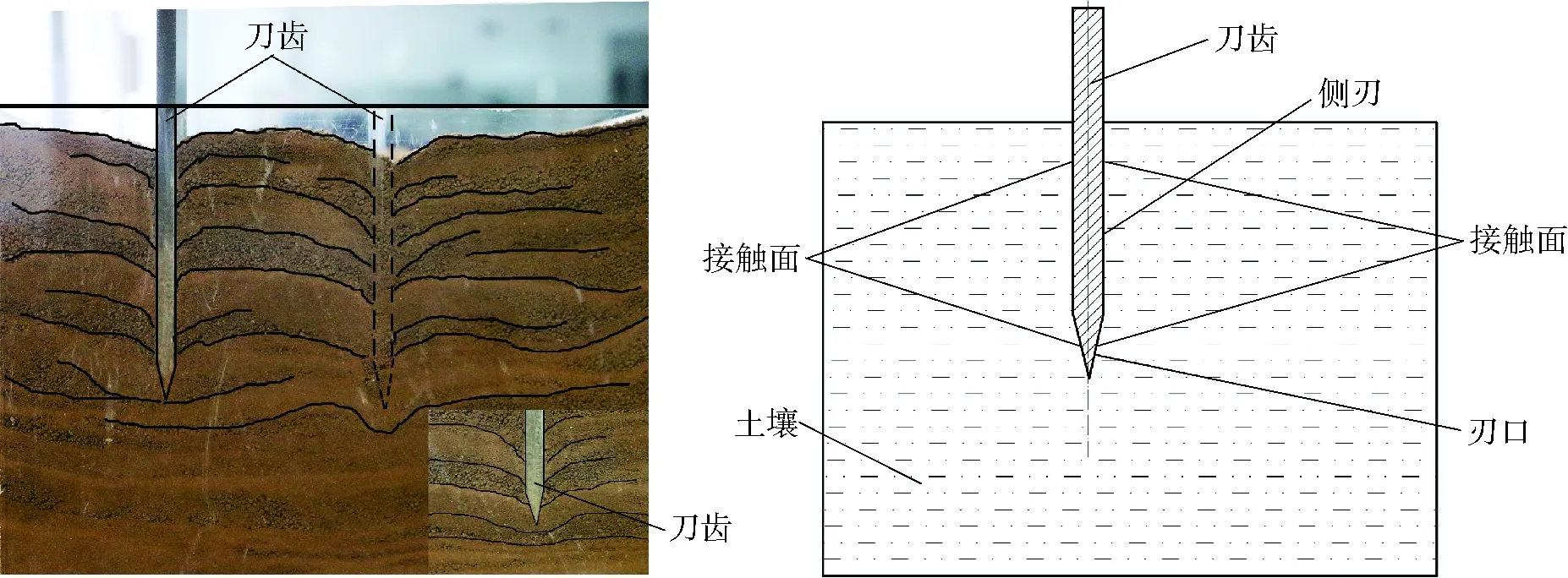
图2 刀齿厚度方向上的土壤截面图Fig.2 Cross section of soil layer in penetration process

观察发现，刀齿在贯入到土壤的过程中，土壤产生了不同程度的形变，沿着刀齿厚度方向上的土壤截面发生扭曲，临近刀齿刃口和侧刃界面的土壤随着刀齿在贯入方向产生向下的位移，而远离刃口和侧刃界面的土壤则表现出与贯入方向相反的竖直向上凸起的位移，尤其是将刀齿以一定的水平间距贯入两次时，相邻2个刀齿之间的土壤向上凸起的特点更加明显。土壤向下凹陷和向上凸起的形变使得土壤褶皱失效，土壤的向上凸起使其获得了一定程度的疏松。

在贯入过程中，刀齿将土壤分开，土壤结构被破坏，土壤受到刀齿刃口和侧刃的挤压，产生弹塑性形变并沿刀齿厚度方向移动，同时土壤沿着刀齿接触面切线方向也发生相对移动。因此刀齿对土壤的作用力可以通过归结为竖直方向和水平方向的作用力(F1和F2)来表示，2个方向上的力使土壤以正方形形心为中心产生逆时针(如图3所示)方向的扭矩，在扭矩的作用下土壤产生褶皱扭曲形变。在此过程中，刀齿与土壤接触面是主要的力学作用界面，作用在接触面上的土壤力学分量成为刀齿在土壤中运动阻力的主要来源，刀齿在土壤中形成了应力场。此外，不同位置的土壤颗粒在贯入力的作用下产生速度和位移，形成了速度场，应力场与速度场共同导致了土壤失效。刀齿导致的土壤失效变形主要发生在与刀具接触面范围内，应力场和速度场造成了土壤局部褶皱和扭曲，但未造成土层翻转等失效现象。

图3 刀齿-土壤相互作用示意图Fig.3 Schematic diagram of tine-soil interaction

1.3 刀齿贯入阻力模型

土壤在受到外力作用后具有抵抗变形和恢复形变的能力[25]，这种能力表现为土壤遭到破坏时作用在刀具上的阻力。通过分析刀齿在贯入过程中造成的土壤失效发现，刀齿在贯入土壤过程中，土壤抵抗机械破坏的粘结力学分量、抗压力学分量、土壤对刀齿的摩擦力学分量和粘附力学分量成为刀齿在土壤中的运动阻力的主要来源，刀齿贯入力与贯入阻力等值反向。由此提出刀齿的贯入阻力模型假设。

刀齿在匀速贯入土壤过程中，假设土壤为均质同向，刀齿的贯入力为

P=N+T+Ca+C

(1)

式中，N、T、Ca和C分别为土壤的抗压力学分量、摩擦力学分量、粘附力学分量和粘结力学分量。

对于带有刃口的刀齿，在贯入土壤过程中，其受力如图4所示。

图4 刀齿贯入土壤时的受力分析Fig.4 Mechanical analysis of tine in penetration stage

图4中，P为贯入力，其大小等于刀齿的贯入阻力；α为刃角，N1为刃口上的法向力，T1为刃口上的摩擦力，Ca1为刃口上的切向粘附力，N2为侧刃上的法向力，T2为侧刃上的切向力，Ca2为侧刃上的切向粘附力，C为土壤粘结力，其大小等于土壤的内聚力[26]。

结合图4，对式(1)展开，得

(2)

式中μ——土壤与刀齿的滑动摩擦因数

其中C与土壤有关，α与刀齿形状尺寸有关，N1、N2、Ca1、Ca2、T1和T2均与土壤和刀齿形状尺寸的综合作用有关。

为进一步验证刀齿贯入阻力模型假设的合理性和准确性，本文以矩形刀齿和三角形刀齿为例，利用室内土槽进行刀齿的贯入试验，重点对刀齿在贯入土壤过程中的受力情况进行探讨与分析。

2 材料与方法

2.1 土槽试验台

试验台包括土槽试验台车和自制试验台，如图5所示。自制试验台主要包括机架、液压缸、支撑架、流量阀、换向阀、位移传感器、拉压力传感器和数据采集装置(包括数据采集器和计算机)。为保证试验时机架与土壤表面在水平方向稳定接触，机架设计成矩形，且带有三点悬挂架，与土槽试验台车通过三点悬挂装置进行固定，液压缸、流量阀和换向阀与试验台车液压系统形成液压回路，用来控制刀齿的运行速度和方向，位移传感器和拉压力传感器用来记录刀齿在运动过程中的位移和受力情况，通过数据采集器采集试验过程中位移传感器和拉压力传感器的数据。

图5 试验台Fig.5 Test bed1.液压缸 2.流量阀 3.换向阀 4.台车 5.机架 6.支撑架7.刀齿 8.数据采集器 9.计算机 10.拉压力传感器 11.位移传感器

2.2 土壤制备

试验所用土槽中的土壤质地与玻璃盒中土壤相同，为尽可能符合田间实际土壤的紧实情况(土壤容重范围为1.2 ～1.5 g/cm3[27])，通过旋耕机和压

实辊先后对土壤进行翻耕、平整和镇压，在镇压前，通过台车上的水管对土槽中的土壤进行浇水，浇水后使土壤静置约48 h，以便水分能充分渗入到土壤中，然后对土壤进行镇压，土壤容重、含水率和孔隙度如表1所示。

表1 不同深度土层的土壤容重、含水率和孔隙度

注：同一列数据字母不同说明在Duncan比较下，显著性水平为0.05的条件下存在显著性差别，下同。

2.3 刀齿运动过程的实现

通过液压系统实现刀齿在土壤中的运动行程和速度控制。矩形刀齿贯入速度为(1.23±0.01) cm/s，拔出速度为(1.76±0.01) cm/s；三角形刀齿的贯入速度为(1.25±0.01) cm/s，拔出速度为(1.83±0.01) cm/s。当刀齿贯入土壤进入稳定阶段后从土壤中拔出，试验时每种刀齿重复3次，通过数据采集器采集传感器中的数据，采集的数据为刀齿所受实际阻力。

2.4 土壤力学特性测定

为验证刀齿贯入阻力的预测模型，对试验中所用土壤的力学特性进行了测定，通过直剪试验和无侧限压缩试验[28]，得到土壤抗剪强度和无侧限抗压强度，结果如表2所示。由于刀齿的厚度为7 mm，与土壤相互作用时对土壤产生的压缩形变比较小，土壤应变小于15%，所以后续在进行模型受力分析时可以根据拟合方程对相应的土壤应变下的无侧限抗压强度进行计算。

表2 各土层土壤内摩擦角、内聚力和无侧限抗压强度试验结果

取足量的土壤试样，通过直剪试验测定土壤与刀齿表面的摩擦因数。试验后绘制抗剪强度(τ)-垂直压力(N)曲线，根据散点图回归得到直线，直线在τ上的截距为土壤与刀齿的切向粘附力，直线的斜率为土壤与刀齿的滑动摩擦因数[29]。滑动摩擦因数和切向粘附力分别为0.170±0.014 6和(2.6±1.238) kPa。

2.5 数据处理分析

通过Excel 2007和SPSS 21.0对试验的数据进行处理和分析，通过Origin 9.0绘制曲线。

3 结果与讨论

结合前文提出的模型假设以及土壤力学特性参数，对矩形刀齿的贯入阻力进行预测和计算，矩形刀齿在贯入过程中的受力情况与图4中所示的受力情况一致。根据矩形刀齿的运动情况，将矩形刀齿的贯入过程分为2个阶段，即贯入深度未超过刃口阶段和超过刃口阶段，由于贯入力与贯入阻力等值反向，后续公式中以贯入力P代表贯入阻力，则矩形刀齿的贯入阻力为

(3)

式中σ1——贯入深度不超过刃口高度阶段的土壤无侧限抗压强度

w——刀齿宽度h——贯入深度

ca——切向粘附力c——内聚力

hr——刃口高度

σ2——贯入深度超过刃口高度阶段的土壤无侧限抗压强度

P0——贯入深度达到刃口高度时贯入阻力

根据矩形刀齿形状尺寸参数和经测量得到的土壤参数，式(3)中各参数赋值如表3所示。σ1根据拟合方程对相应的土壤应变下的无侧限抗压强度进行计算(下同)。

对于三角形刀齿，在贯入土壤过程中，刀齿刃口是逐渐贯入土壤的，对其在贯入过程中的受力进行

分析，如图6所示。

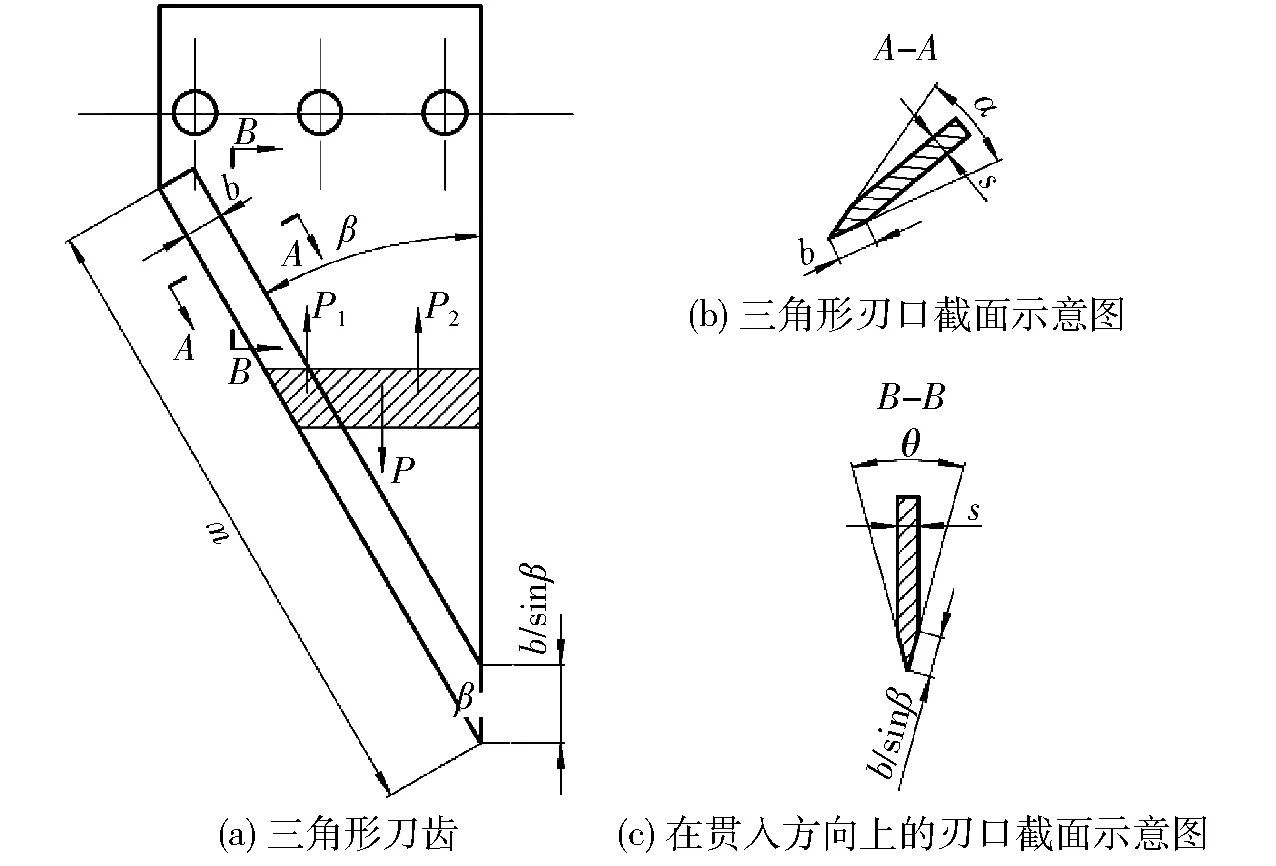
图6 三角形刀齿贯入过程中的受力分析Fig.6 Mechanical analysis of triangle tine in penetration stage

图6中，P为贯入力，P1为刃口贯入阻力的合力，P2为侧刃贯入阻力的合力，s为刀刃厚度，α为刃角，b为刃口宽度，β为三角形刀齿顶角，θ为三角形刀齿在贯入方向上的刃角。

由于三角形刃口部分是逐渐贯入土壤的，且刃口方向与竖直方向呈30°夹角，所以在实际贯入方向上的刀齿刃角并不为30°，应为刀齿刃口贯入方向(垂直方向)上的刃口截面所对应的刃角(θ)，则

(4)

(5)

本文将图6中b/sinβ部分作为三角形贯入土壤时刃口的高度，则在贯入阶段，三角形刀齿的贯入阻力为

(6)

根据三角形刀齿形状尺寸参数和经测量得到的土壤参数，式(6)中各参数赋值如表4所示。σ1根据拟合方程对相应的土壤应变下的无侧限抗压强度进行计算，刃口部分以刃口中线处对应的土壤应变计算。

分别根据式(3)和式(6)对刀齿的贯入阻力进行计算，并绘制贯入阻力预测曲线，同时将试验值与模型预测值进行比较，结果如图7所示。实际试验 中采集到的刀齿受力的数据单位为kg，为方便进行比较，对单位进行统一，将实际试验值乘上9.8，转化为N(后同)。

表4 三角形刀齿贯入阻力模型参数

从图7中可以看出，矩形刀齿的贯入阻力随贯入深度变化曲线存在拐点，在初始阶段贯入阻力随着贯入深度急剧增加，而后平缓增加，三角形刀齿在整个贯入阶段，贯入阻力随贯入深度的变化并没有显著的阶段性差别。矩形模型曲线与实际试验曲线变化趋势一致，均呈先急剧增加然后再平缓增加的特点，并且在曲线拐点两侧均呈不同斜率的线性变化趋势。三角形刀齿均以某一规律呈非线性增加的特点，模型曲线与实际试验曲线相比，曲线变化趋势较为平稳。从变化趋势上来看，预测模型可以用来预测刀齿在贯入土壤过程中贯入阻力随贯入深度的变化趋势。

图7 刀齿受力随贯入深度变化关系曲线Fig.7 Relationship curves between penetration resistance and depth

通过对刀齿贯入阻力模型假设和与实际试验曲线的对比分析，说明可以通过土壤的力学分量来预测刀齿的贯入阻力。比较模型预测曲线和实际试验曲线，发现预测模型所呈现出的刀齿贯入阻力随贯入深度的变化趋势与实际试验中的变化趋势一致，验证了刀齿贯入阻力预测模型的合理性。KOSTRITSYN建立了纯切削力学计算模型，只考虑土壤变形破坏后对刀具所引起反力的平衡，而不过多陷入变形和破坏的细节，从受力平衡得出切削阻力[30]。本文所假设的模型与纯切削模型相似，即在受力平衡的基础上，对带有刃口和侧刃的刀齿进行受力分析，都是得到刀齿的切削阻力，不同的是，本文将刀齿破坏土壤粘结力以及土壤和刀齿的粘附力考虑了进去，在纯切削模型的基础上进行了进一步分析，这一点与HETTIARATCHI等[31-32]和GODWIN等[33-34]的研究相似。

同时可以看出，矩形刀齿受力曲线的拐点处所对应的深度要大于刀齿的刃口高度，结合前文所述的土壤失效机理分析，其原因与土壤的失效过程有关，土壤在此深度下达到失效的临界值。本文以临界深度(hl)来描述拐点处对应的贯入深度，刀齿在贯入土壤过程中，刀齿刃口部分对土壤产生挤压，经过挤压的土壤变得紧实，土壤密度增加，抗压强度增加，所以贯入阻力随着贯入深度呈急剧增加的特点，而当贯入深度超过刃口高度而未达到临界深度时，土壤由于刃口的挤压，其抗压强度与初始状态相比要大一些，所以超过刃口高度和临界深度之间的贯入阻力在刃口部分的贯入阻力的基础上仍保持原来的特点继续增加，而当贯入深度超过临界深度以后，土壤各土层产生松动失效，导致土壤对刀齿的抗压强度有所减弱，刀齿贯入阻力随着贯入深度的变化趋势有所降低。而三角形刀齿在贯入土壤过程中刃口是逐渐入土的方式，土壤也是逐渐失效的，因此临界深度的特点也不如矩形刀齿刃口完全贯入的方式表现得明显，贯入阻力随深度的变化趋势并不如矩形刀齿如此明显，而是逐渐以稳定趋势变化的。

另外，通过假设模型预测的刀齿贯入阻力在整个贯入过程中都要比实际试验过程中的刀齿贯入阻力小，并且两条曲线的差距随着深度变化总是变化的，并不完全呈一致的线性或其他规律变化，其原因主要是预测模型是在假定土壤为均质各向同性的情况下提出的，而实际中土壤各向异性，整个运动过程中土壤的力学性质变化也比较复杂，另外就是在实际试验过程中，刀齿的厚度对刀齿的贯入阻力也会产生一定的积极影响，所以实际试验过程中的贯入阻力要比模型预测值大。

结合刀齿贯入阻力预测模型，针对刀齿受力曲线的各个阶段，比较预测值与试验值之间的关系，如表5所示。

由于实际试验时矩形刀齿在贯入深度超过临界深度后，贯入阻力波动较大，所以R2相对较小。从表5中可以看出，实际试验值与预测值之间呈良好的线性拟合关系，说明刀齿贯入阻力的预测模型存在修正常数，HETTIARATCHI等[32]对宽齿刀具在土壤中运动进行受力预测时，对各个力学分量进行了修正，将土壤对刀齿的各个力学分量前边的系数

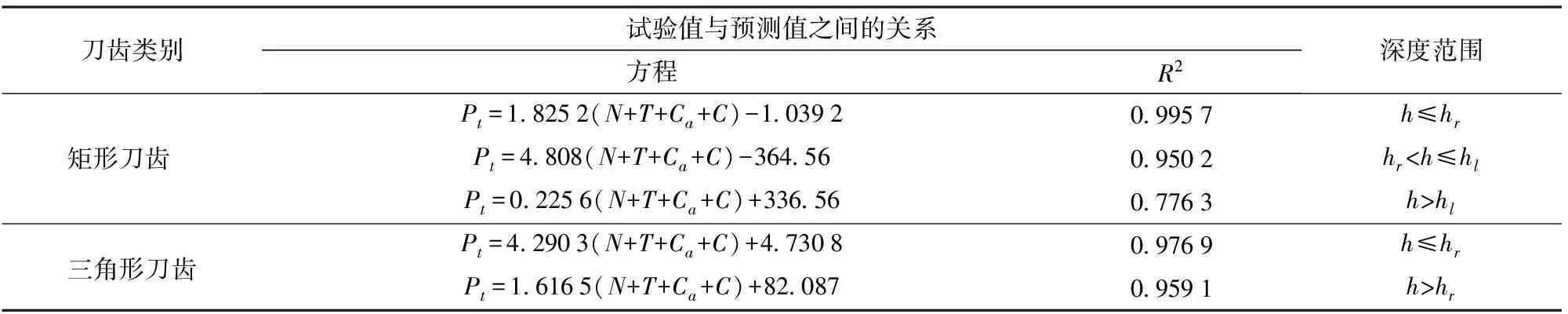
表5 试验值与预测值比较

注：Pt为实际试验的贯入阻力。

定义为与刀具入土倾角和土壤内摩擦角有关的无量纲常数，现有的研究中也发现土壤的类型、密度和含水率均会对贯入阻力产生影响[35]，结合模型曲线与实际试验曲线的对比分析，可以推断出，对于本文提出的刀齿贯入阻力预测模型可进行修正，即式(1)可修正为

P=k(N+T+Ca+C)+e

(7)

式中，k和e为与土壤物理性质有关的修正常数，但仍需要通过进一步的试验分析才能确定模型修正常数与土壤参数之间的关系及相关的变化规律。通过对预测模型的分析和讨论可以得出，本文所提出的预测模型能够很好地预测极窄类刀齿的贯入阻力随贯入深度的变化关系，同时对于极窄类带有刃口的刀齿类工作部件(这类刀齿贯入土壤的深度远大于贯入的厚度)在土壤中运动时的工作阻力、造成的土壤失效情况以及相关机具功耗的计算等方面具有一定的理论参考价值。

进一步分析可以看到，矩形刀齿的临界深度在30 mm左右，而此深度下贯入阻力平均为382.396 N，三角形刀齿在该深度下的贯入阻力仅为矩形刀齿的19.34%，贯入深度超过临界深度后，三角形刀齿的贯入阻力逐渐接近矩形刀齿的贯入阻力，但三角形刀齿的贯入阻力随贯入深度的变化曲线中并没有明显的变化趋势转折点，进一步说明了刀齿刃口的形状和尺寸对刀齿贯入土壤过程中的贯入阻力有较大的影响，且刃口以完全入土的方式贯入时(矩形齿)，临界深度的特点表现的比较明显。

通过CATIA软件绘制1∶1刀齿模型，并计算各深度下的刀齿与土壤的接触面积，绘制贯入阶段刀齿贯入阻力与接触面积的关系曲线，如图8所示。

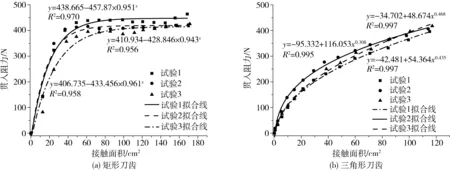
图8 贯入阶段刀齿受力随接触面积变化曲线 Fig.8 Relationship curves between penetration resistance and attack surface area of tines in penetration stage

从图8中可以看出，2种刀齿的贯入阻力随接触面积变化而呈非线性变化，但2种刀齿的变化曲线也有所不同，三角形刀齿的贯入阻力随接触面积变化以某一规律逐渐增加，这一规律可以通过幂函数(R2>0.99)来进行描述；而矩形刀齿贯入阻力随接触面积先急剧增加，然后再平缓增加，可以用指数性变化来描述(R2>0.95)，这一规律与图7中的变化规律相似。

刀齿与土壤的接触面积主要包括了刀齿刃口和侧刃与土壤的接触面积。贯入阻力随接触面积呈幂函数变化的趋势与很多学者在对圆板压头、矩形平板和平面圆压头等部件进行贯入试验时发现的规律相似[30]，但不同类型的工作部件所呈现的表达式有所差异。ZELENIN[36]通过水平切刀进行大量的试验，也观察到阻力和耕作深度之间存在抛物线关系。对于规则的工作部件来说，与土壤的接触面积可以通过其耕作深度和宽度等尺寸参数计算得到，因此，贯入阻力或者切削阻力与贯入深度之间的非线性变化关系可以间接地反映出贯入阻力或切削阻力与接触面积之间的变化规律。在对极窄刀齿在贯入土壤的有限元仿真试验中，得到刀齿贯入阻力与接触面积之间相似的幂函数变化关系，并且幂函数变化的趋势随着刀齿厚度的变化而呈现出不同的特点[37]。这进一步验证了极窄刀齿的形状尺寸参数对其贯入阻力有很大的影响，在设计极窄类刀齿或者对极窄类刀齿进行受力分析时，刀齿的形状尺寸参数是首要考虑的因素。矩形刀齿的贯入阻力与接触面积之间的关系与三角形刀齿呈现出相似又不同的特点，这主要也与不同形状尺寸参数的刀齿在贯入时所造成的土壤失效情况不同有关。

另外，对比矩形刀齿和三角形刀齿的贯入阻力随深度的变化曲线，三角形刀齿在贯入过程中不存在贯入阻力急剧变化的情况，相对矩形刀齿来说比较稳定，且贯入阻力在贯入过程中都要比矩形刀齿小。

4 结论

(1)极窄刀齿在贯入土壤过程中，土壤在与刀具接触面范围内，与刀齿耦合形成应力场和速度场，土壤产生褶皱扭曲形变进而失效，同时在贯入过程中存在刀齿致使土壤失效的临界深度，且刃口以完全入土的方式所展现的临界深度的特点更为明显。

(2)刀齿与土壤之间的相互作用力可以通过土壤的力学分量来计算和预测；刀齿在贯入土壤过程中的阻力主要由土壤抵抗机械破坏的粘结力学分量、抗压力学分量、土壤对刀齿的摩擦力学分量和粘附力学分量组成，通过上述力学分量可以预测和计算刀齿的贯入阻力。

(3)提出了刀齿在贯入土壤过程中的贯入阻力预测模型并进行了修正，即P=k(N+T+Ca+C)+e，并在室内土槽土壤(砂粒44.6%，粉粒35%和粘粒20.4%)条件下进行了验证，预测模型能够较好地反映出极窄刀齿贯入阻力随深度的变化情况，同时说明极窄刀齿的形状尺寸参数是影响其贯入阻力的重要因素。

1 GODWIN R J, O’DOGHERTY M J. Integrated soil tillage force prediction models [J]. Journal of Terramechanics, 2007, 44(1): 3-14.

2 BUCKRELL A, GRAHAM W. Soil aeration device having close-coupled shafts: US 8,297,372[P]. 2012-10-30.

3 ALSTRONG. Alstrong aerators [EB/OL]. http:∥www.alstrong.ie/our-machines/.2016-8-24.

4 DE BREE C H M. Soil aeration device: US 8,056,645[P]. 2011-11-15.

5 尤泳，王德成，王光辉. 9QP-830型草地破土切根机[J].农业机械学报，2011，42(10)：61-67. YOU Yong, WANG Decheng, WANG Guanghui. 9QP-830 soil-gashing and root-cutting mechanism [J].Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(10): 61-67. (in Chinese)

6 梁方. 草地切根施肥补播复式改良机械的优化设计与试验研究[D].北京：中国农业大学, 2015. LIANG Fang. Optimization design and experiment study on root-cutter with fertilization and reseeding compound remediation machine for grassland[D]. Beijing: China Agricultural University, 2015. (in Chinese)

7 MATIN M A, DESBIOLLES J M A, FIELKE J M. Strip-tillage using rotating straight blades: effect of cutting edge geometry on furrow parameters [J]. Soil and Tillage Research, 2016, 155: 271-279.

8 KARMAKAR S, KUSHWAHA R L. Dynamic modeling of soil-tool interaction: an overview from a fluid flow perspective [J]. Journal of Terramechanics, 2006, 43(4): 411-425.

9 翟力欣. 犁体结构与工作参数对流变型土壤耕作阻力的影响研究[D]. 南京：南京农业大学, 2011. ZHAI Lixin. Study on the effects of plough’s working and structure parameters on its resistance under rheological soil conditions [D]. Nanjing： Nanjing Agricultural University, 2011.(in Chinese)

10 余浩. 窄齿土壤工作部件几何特性与减阻性能研究 [D]. 洛阳：河南科技大学, 2015. YU Hao. The study of drag reduction performance of narrow tooth soil working parts with its geometric characteristics [D]. Luoyang： Henan University of Science and Technology,2015.(in Chinese)

11 张智泓. 田间土壤表面微形貌加工滚动触土部件与土壤相互作用及仿生几何结构 [D]. 长春：吉林大学, 2014. ZHANG Zhihong. Interaction of soil and rolling soil engaging components for micro-topographical preparation and their bionically geometrical structures [D].Changchun： Jilin University, 2014.(in Chinese)

12 HEMMAT A, RAHNAMA T, VAHABI Z. A horizontal multiple-tip penetrometer for on-the-go soil mechanical resistance and acoustic failure mode detection [J]. Soil and Tillage Research, 2014, 138: 17-25.

13 BÖGEL T, OSINENKO P, HERLITZIUS T. Assessment of soil roughness after tillage using spectral analysis [J]. Soil and Tillage Research, 2016, 159: 73-82.

14 DÖRNER J, HORN R. Direction-dependent behaviour of hydraulic and mechanical properties in structured soils under conventional and conservation tillage [J]. Soil and Tillage Research, 2009, 102(2): 225-232.

15 LISOWSKI A, KLONOWSKIJ J, GREEN O, et al. Duckfoot tools connected with flexible and stiff tines: three components of resistances and soil disturbance [J]. Soil and Tillage Research, 2016, 158: 76-90.

16 HASIMU A, CHEN Y. Soil disturbance and draft force of selected seed openers [J]. Soil and Tillage Research, 2014, 140: 48-54.

17 SALAR M R, ESEHAGBEYGI A, HEMMAT A. Soil loosening characteristics of a dual bent blade subsurface tillage implement [J]. Soil and Tillage Research, 2013, 134: 17-24.

18 王国林, 马旭. 耕作层土壤在动载作用下的力学特性[J]. 农业机械学报, 1997, 28(2): 6-10. WANG Guolin, MA Xu. Study on the mechanical properties of tillage soil under the action of dynamic load [J]. Transactions of the Chinese Society for Agricultural Machinery, 1997, 28(2): 6-10.(in Chinese)

19 佟金, 张智泓, 陈东辉, 等. 凸齿镇压器与土壤相互作用的三维动态有限元分析[J]. 农业工程学报, 2014, 30(10): 48-58. TONG Jin, ZHANG Zhihong, CHEN Donghui, et al. Three-dimensional dynamic finite element analysis of interaction between toothed wheel and soil [J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(10): 48-58.(in Chinese)

20 方会敏, 姬长英, AHMED Ali Tagar, 等. 秸秆-土壤-旋耕刀系统中秸秆位移仿真分析[J/OL]. 农业机械学报, 2016, 47(1): 60-67. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160109&flag=1.DOI：10.6041/j.issn.1000-1298.2016.01.009. FANG Huimin, JI Changying, AHMED Ali Tagar, et al. Simulation analysis of straw movement in straw-soil-rotary blade system [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1): 60-67.(in Chinese)

21 GODWIN R J. A review of the effect of implement geometry on soil failure and implement forces [J]. Soil and Tillage Research, 2007, 97(2): 331-340.

22 KUCZEWSKI J, PIOTROWSKA E. An improved model for forces on narrow soil cutting tines [J]. Soil and Tillage Research, 1998, 46(3): 231-239.

23 ONO I, NAKASHIMA H, SHIMIZU H, et al. Investigation of elemental shape for 3D DEM modeling of interaction between soil and a narrow cutting tool [J]. Journal of Terramechanics, 2013, 50(4): 265-276.

24 ZHANG J, KUSHWAHA R L. A modified model to predict soil cutting resistance [J]. Soil and Tillage Research, 1995, 34(3): 157-168.

25 BALL B C, BATEY T, MUNKHOLM L J. Field assessment of soil structural quality—a development of the Peerlkamp test[J]. Soil Use and Management, 2007, 23(4): 329-337.

26 农业辞典编辑委员会.农业辞典[M].南京:江苏科学技术出版社,1978.

27 贺长彬, 尤泳, 王德成, 等. 退化草地复合体力学特性与影响因素研究[J/OL]. 农业机械学报, 2016, 47(4):79-89. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160412&flag=1.DOI：10.6041/j.issn.1000-1298.2016.04.012. HE Changbin,YOU Yong,WANG Decheng, et al. Soil-root composite mechanical characteristics and its influence factors of degenerated grassland [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4):79-89. (in Chinese)

28 GB/T 50123—1999 土工试验方法标准[S].1999.

29 任露泉. 土壤粘附力学[M]. 北京：机械工业出版社，2011.

30 曾德超. 机械土壤动力学[M]. 北京：科学技术出版社, 1995.

31 HETTIARATCHI D R P, WITNEY B D, REECE A R. The calculation of passive pressure in two-dimensional soil failure [J]. Journal of Agricultural Engineering Research, 1966, 11(2):89-107.

32 HETTIARATCHI D R P, REECE A R. The calculation of passive soil resistance [J]. Geotechnique, 1974, 24(3): 289-310.

33 GODWIN R J, SPOOR G. Soil failure with narrow tines[J]. Journal of Agricultural Engineering Research, 1977, 22(3): 213-228.

34 GODWIN R J, SPOOR G, SOOMRO M S. The effect of time arrangement on soil forces and disturbance [J]. Journal of Agricultural Engineering Research, 1984, 30: 47-56.

35 李艳洁, 林剑辉, 徐泳. 圆锥指数仪贯入沙土试验的离散元法模拟[J]. 农业机械学报, 2011, 42(11): 44-48. LI Yanjie, LIN Jianhui, XU Yong. Discrete element simulations of the cone penetration tests in sandy soil [J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(11): 44-48.(in Chinese)

36 ZELENIN A N. Basic physics of the theory of soil cutting[R]. Moscow-Leningrad: Akademia Nawk USSR, 1950.

37 HE C, YOU Y, WANG D, et al. The effect of tine geometry during vertical movement on soil penetration resistance using finite element analysis[J]. Computers and Electronics in Agriculture, 2016, 130: 97-108.

Interaction Relationship between Soil and Very Narrow Tine during Penetration Process

YOU Yong1HE Changbin1WANG Decheng1,2WANG Guanghui1

(1.CollegeofEngineering,ChinaAgriculturalUniversity,Beijing100083,China2.LaboratoryofSoil-Machine-PlantSystematicTechnology,MinistryofAgriculture,ChinaAgriculturalUniversity,Beijing100083,China)

With the development of the conservation tillage technology and low disturbance soil treatment, new tillage tools like narrow or very narrow tines are applied more often. In order to provide theoretical supports for the design and optimization of tillage tools and key components, and enrich the theory system of soil-tool interaction, the very narrow tine-soil interaction was investigated, especially during the penetration process. Two tines with different cutting edge shapes were designed and a special test bed was set up based on the soil bin test bench as well. Soil failure mechanism was analyzed. The resistances of the two tines were recorded, analyzed and compared in the penetration stage. And the resistance prediction mechanical models were proposed. The mean resistance sources of the tines were found by analyzing the tines resistance mechanical models. The contact areas of the very narrow tines in different depths were measured and calculated by using the CATIA three-dimensional design software, and the relationships between the resistances and contact areas were analyzed as well. Results indicated that soil failure was mainly caused by the stress field and velocity field in the soil-tine interaction. Mechanical components of soil cohesive, pressure, friction and adhesion were the main resistance sources of the tines. The forces between the tines and soil can be predicted by the soil mechanical components. The prediction models can well reflect the tendency between the resistances and the depth in the tines working processes. Furthermore, the results indicated that there was a nonlinear relationship between the resistance and soil-tine contact area with certain soil property parameters. The tine geometry parameter became an important influence factor of the resistance.

soil tillage tool; very narrow tine; soil failure mechanism; prediction model; interaction relationship

10.6041/j.issn.1000-1298.2017.06.006

2016-11-23

2016-12-15

国家自然科学基金青年科学基金项目(51405493)和现代农业产业技术体系专项资金项目(CARS-35)

尤泳(1980—)，男，博士，主要从事土壤-根系-刀具作用关系基础性研究和牧草机械研究，E-mail： youyong@cau.edu.cn

王德成(1965—)，男，教授，博士生导师，主要从事农业机械化工程研究，E-mail： wdc@cau.edu.cn

S220.1； S152.9

A

1000-1298(2017)06-0050-09