基于梁-梁接触理论的管柱屈曲分析

王尊策, 曹梦雨, 徐德奎, 温后珍, 徐 艳, 陈 明, 吕凤霞

(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318; 2.北京工业大学机械工程与应用电子技术学院,北京 100124;3.常州大学机械工程学院,江苏常州 213016)

基于梁-梁接触理论的管柱屈曲分析

王尊策1, 曹梦雨1, 徐德奎2, 温后珍1, 徐 艳1, 陈 明1, 吕凤霞3

(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318; 2.北京工业大学机械工程与应用电子技术学院,北京 100124;3.常州大学机械工程学院,江苏常州 213016)

为探究长直管柱在井下复杂工况下的屈曲形式,进行基于梁-梁接触理论的管柱屈曲分析研究。利用梁-梁接触理论对考虑剪切弯曲变形的梁进行离散化,使用管-管接触单元建立管柱变截面摩擦接触有限元模型,并用此方法针对分层采油井实际井况建立管柱有限元分析模型。结果表明,分层采油管柱在井下复杂的受力环境下会发生不等距复合屈曲,在考虑摩擦的情况下管柱的屈曲构型不再是标准的正弦线或是螺旋线构型,并利用磁定位数据验证了计算结果的可靠性。

管柱; 管-管接触单元; 梁-梁接触理论; 摩擦接触; 复合屈曲; 磁定位; 井下工具

油套环空间隙值极小,油管变形时与套管的接触作用反过来又会影响油管的变形形式,导致管柱在井下的受力变形情况极为复杂。在严格意义上说,石油管柱力学问题是一个包含接触非线性和几何非线性在内的三维二重非线性力学问题[1],受井眼约束的油管[2]承载的外载超过一定数值时,将会失去原有的直线稳定状态而发生屈曲。其屈曲行为将先后经历前屈曲和后屈曲两个过程,其中前屈曲行为与屈曲临界载荷、分叉点等参数有关,而后屈曲过程则与管柱结构的有限变形有关[3]。屈曲行为将造成油管上安装的封隔器、配产器等工具发生轴向和径向的移位,分别导致注采串层以及工具偏心后的偏磨现象,引起工具失效等问题,严重时将导致油田生产事故的发生,造成重大的经济损失。李子丰等[4]分析了热采过程中套管柱在井内的受力状态,给出了套管柱强度校核方法与应用实例,在对套管进行受力分析时未考虑油管与套管之间的接触摩擦作用;Lubinski[5]、Mitchell等[6-9]分别基于不同方法先后得到了管柱在轴向载荷下的屈曲行为及接触力方程,方程中未考虑摩擦力的影响;高德利等[2]系统分析了受井眼约束管柱的屈曲等问题以及摩擦对屈曲的影响,分析时未考虑管柱与井眼脱离对屈曲构型的影响。涉及摩擦接触的管柱变形问题极难处理,而非线性有限元是较为有效的处理方法。狄勤丰等[10-11]采用有限元迭代法研究了柔性短节位置对带旋转导向工具底部钻具动力学特性的影响,建立了钻柱动力学系统平衡方程;刘巨保等[12]使用间隙元理论建立了基于梁单元的钻柱力学分析模型,极大推进了钻柱接触非线性分析进程,但间隙元模型是一种平面单元,实际管柱的受力变形情况是一种三维情形。为建立分层采油管柱于各工况作用下的三维变形情况分析方法处理考虑摩擦与轴向位移在内的梁-梁三维接触问题,笔者应用管-管接触单元基于梁-梁接触理论建立分层采油井的摩擦接触有限元模型,针对中33-P250分层采油井的实际工况进行数值分析,磁定位测井结果证明此方法在预测井下工具轴向位置串动的可行性。

1 平衡方程

由于采油管柱的长径比极大,在分析整趟管柱的受力变形情况时,很难按1∶1建立实体模型进行分析,故采用梁单元对采油管柱进行简化建模,常用的梁模型主要有铁木辛柯梁模型和欧拉-伯努利梁模型两种,其中欧拉伯努利梁理论未考虑梁的剪切变形,为铁木辛柯梁理论[9]的简化。

设梁的受力示意图如图1所示,其中,P(x)为横向作用的均布载荷,M和Fs分别为弯矩和剪力,梁的轴向载荷对称于x-z平面。令ψ(x)为横截面的转角,以顺时针为正,依据广义胡克定律[13]可推知:

(1)

式中,E、G分别为弹性模量和剪切模量,MPa;σxx、σxz分别为横截面上沿x轴和z轴方向的正应力;k2为剪切系数,表示梁的横截面上平均剪应变与横截面形心处的剪应变之比,其数值与横截面形状有关。

应用静力平衡方程以及平面格林定理等进行推导,最终可得到用位移表示的包含了梁弯曲变形以及剪切变形的平衡方程为

(2)

式中，A为横截面面积，mm2;I为轴横截面对中心的惯性矩，mm4。

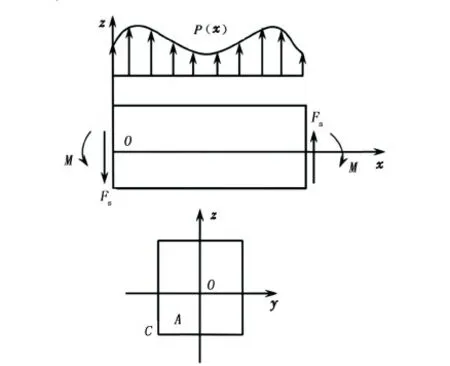
图1 铁木辛柯梁典型受力形式Fig.1 Typical stress form of Timoshenko beam

由于管柱在井下有可能产生剪切变形,故本文分析中建立的数值分析[14]模型基于铁木辛柯梁平衡方程。管柱力学使用的分析方法有微分方程法、纵横弯曲连续梁法、加权残数法、有限单元法、有限体积法[15]、有限差分法等多种,其中有限差分法在管柱力学中应用较多,而使用非线性有限元方法对整趟管柱的随机多向变截面接触问题的研究并不多见,但有限元法具有物理概念简单清晰、管柱材料与几何形状任意、非线性作用容易考虑等优点,在处理此类问题方面具备极大潜力。

2 梁-梁接触中的有限元法

2.1 接触分析引入

采油管柱中存在着内外管之间的摩擦接触,故在建立有限元分析模型时须将接触定义引入模型。接触分析是一种纯数学分析,考虑了几何约束,使用建立穿透函数的方式判别接触是否发生,穿透函数的函数值为两物体上选定点之间的距离,当穿透函数的函数值小于零时接触发生。

2.2 接触分析中的有限元法

使用有限元方法进行接触分析时,约束与从面与主面的每一组接触点相对应。对接触体离散化时也须对约束进行离散化[16]。接触分析中使用的接触单元大致如图2所示。其中最简单的单元为(a)中所示点对点单元,它既可以用于二维模型分析又可以用于三维模型分析,但是只能处理小位移以及小应变情况;如果问题中接触体之间发生很大的相对位移时,则须用点对段单元或点对面单元;梁-梁接触时所用单元则属于不同的种类,这类单元没有主从区别,且接触点与从属节点不一致,而是处于两个梁单元的节点之间。在有限元分析中,被简化成梁单元的物体往往3个方向上的尺寸存在很大差别,其中一个方向上的尺寸远大于其余两个方向的尺寸,故梁单元在建模时往往简化为一条沿轴线的三维曲线,且认为梁-梁接触是逐点接触。

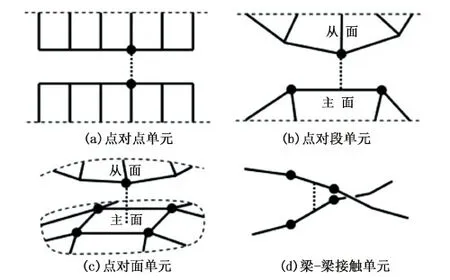
图2 四种接触单元Fig.2 Four kinds of contact elements

2.3 梁-梁接触的存在判定

在逐点接触的前提下,欲定义两根梁之间的穿透函数须首先寻找两梁轴线上的最近点对Cmn和Csn。此时两条曲线上的任意点位置由曲线的局部坐标ξm和ξs分别定义,如图3所示,其中下标m和s不代表主从关系,仅为了区别不同梁。在梁-梁接触中没有主从之分,两根梁的处理方式是一样的。

梁单元的穿透函数必须基于梁的当前构型指定,故曲线上的每一个点都指定了一个位置矢量:xm或xs,位置矢量与相应连接矢量xmn,m(或xsn,s)的数量积为零。在处理变形过程的每一个迭代时,这些矢量都对应着当前梁构型,且为初始构型矢量Xm和位移矢量um的矢量和。以梁m为例,有下列矢量关系:

(xmn-xsn)·xmn,m=0,

(3)

xm=Xm+um.

(4)

式中，xmn,m为位置矢量xmm对局部坐标ξm求取偏导数。

通常情况下,梁的初始轴线(或初始边线)在经历变形时,式(3)将会推导出一个非线性方程组,其解集可以按照局部坐标ξm和ξs的形式写出,这一结果描述了最近点对的位置,可以由牛顿迭代法求解,计算过程中须求解局部坐标增量Δξm和Δξs,将结果线性化处理为

(5)

其中,D为矩阵简写,展开式为

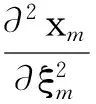
图3 梁轴线上的最近点Fig.3 The closest approach on beams axial line

基于上述数值关系求出最近点对的位置后,可以计算它们之间的距离dN:

(6)

当梁的半径分别为rm和rs时,则穿透函数gN与接触之间的关系为

gN=dN-rm-rs.

(7)

若gN<0,则发生穿透,判定接触存在。

3 摩擦接触模型

3.1 管-管接触单元

使用管-管接触单元[17]处理梁与梁之间的内外接触[18]问题,它是一种滑移线接触单元,可以在两条管线之内或之间建立起滑移线接触。管-管接触单元可用于梁、管、桁架模型的建立,每一个单元均使用一个节点定义,使用滑移线和接触单元集分别定义接触的主面与从面。

3.2 单元接触方程

管-管接触[19]假定存在有限的间隙,内管处理为从面,外管处理为主面。单元的接触方程可以表示为

-n(h+h0)=x1-x.

(8)

x为外管上一点,而其可能接触的点x1则在内管上,如图4所示,方程中h0是管间的径向间隙。

接触方程可以表示为

-n(h+h0)=-Ni(g)xi.

(9)

式(8)与式(9)的形式完全相反,这一特点与常规滑移线单元接触时的内外环境对比相关,式(9)的线性化形式为

δn(h+h0)+nδh=-tδs-Niδxi.

(10)

假定接触时h=0,接触方向定义为

δh=-Ni·n·δxi.

(11)

在沿管方向上有δs=-h0t·δn-Ni·t·δxi,借助于n·t=0可以推得:

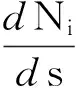
(12)

式中,ρn为曲线的曲率。

借助横断面的本地切线方向s可以导出方程为

δs2=-Ni·s·δxi=h0s·δn.

(13)

方程(13)中初始应力刚度条件可以通过求解h0、s以及s2的二阶导数求出。

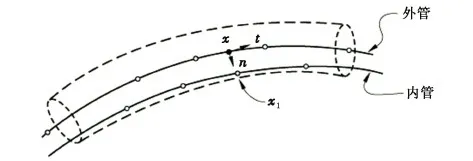
图4 管管接触Fig.4 Tube-to-tube contact

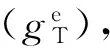
(14)

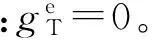
式中,∏为势能函数;εN和εT均为罚参数;λT为拉格朗日算子。

用有限元方法研究管柱力学问题虽然有诸多优势,但在处理油套随机多向摩擦接触方面显得十分困难,这主要是由于有限单元法在处理这种随机多向接触问题时须反复进行位移判断、边界条件修改等工作,这些处理工作均增加了迭代运算的工作量;而且管柱往往长达数千米,管柱上各种工具的材料、尺寸、与套管的摩擦系数等参数均不尽相同,这些因素均会增加管柱屈曲分析的收敛难度。为解决这一难题,基于有限元方法针对实际井况优化建立了油套管的多段变截面随机摩擦接触模型,此模型中对油套接触区域进行了分散处理,降低和减少了接触搜索的难度与工作量,使模型收敛性提升。

4 算例分析

中33-P250井是分层产量控制工艺管柱,由丢手接头、平衡式油井封隔器、可调配产器、连通器等26段结构组成,是一种平衡式支井底丢手管柱,此类管柱结构如图5所示。

图5 管柱结构示意图Fig.5 Schematic diagram of string structure

设计思路为封隔器将分层配产层段卡开,两级封隔器之间接可调配产器,管柱上部接有丢手接头,管柱下部接有连通器。管柱工作状态共4种,分别为自由支井底状态、坐封状态、丢手状态和采油状态,各状态下管柱的受力形式不同,现针对其自由支井底状态进行数值分析。

4.1 力学模型

采用梁结构对中33-P250井的油套管结构进行简化。根据管柱结构,油管上共安置有7个封隔器、6个可调配产器以及一个连通器等主要工具。渲染并放大截面形状后油管的力学模型如图6所示。

图6 油管力学模型Fig.6 Mechanical model of pipe

建模时各零部件的几何尺寸及材料选择如表1所示。

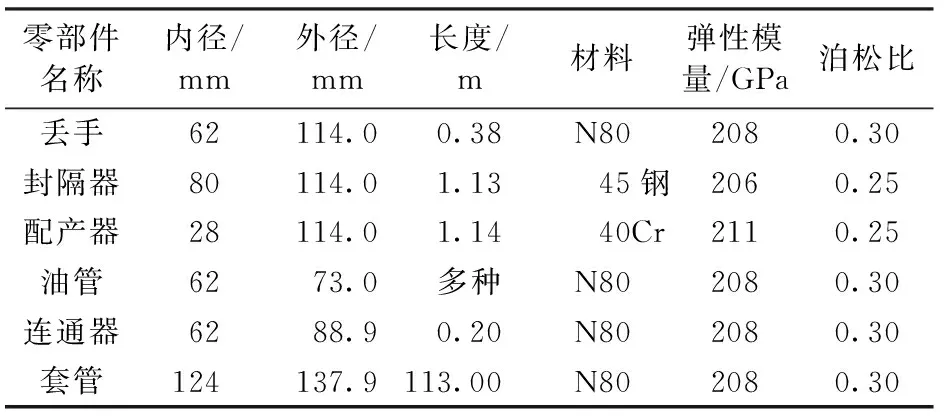
表1 几何及材料参数Table 1 Geometrical and material parameters

4.2 分段摩擦接触模型

由于分析的重点在于油管在套管约束下的屈曲构型,并非工具变形,故为了降低计算难度,忽略了不同工具的内部结构,仅将各工具简化处理为相应截面尺寸的钢结构,并在建立接触时对油管结构依据管径与材料的不同分段建立接触关系,减小同一接触对的接触单元集总长度,以降低接触搜索时的难度。

由于采用梁单元建立同心的油套管柱时,油管与套管都是一条线,无法用常规方法建立接触,故基于建立的分段摩擦接触方法,在模型输入文件中添加油管与套管之间的管管接触定义,其中由于自由支井底工况下封隔器未坐封,橡胶材料的接触非线性和材料非线性均未过多在计算中体现,但若对其材料属性详细定义则增加了模型计算代价。故在定义材料时仅对其刚性部件的材料属性进行定义,并未定义会严重影响收敛性的胶筒部分,而在摩擦系数定义时则按照橡胶与套管的摩擦系数进行定义,降低了计算代价。根据管柱结构特点,中33-P250井共建立26对不同属性的接触,根据相应试验结果,封隔器与套管之间的摩擦系数取0.3,而油管、配产器和连通器等工具与套管之间的摩擦系数则定义为0.05。

4.3 载荷与边界条件

中33-P250井分五层采油,在自由支井底工况下,由于封隔器没有坐封,管柱主要承受丢手上作用的压力F1(78 kN)、管柱自重G、管柱下端面液压力F2(11 kN)、井底的支反力F3、管柱与套管之间摩擦力f等的作用。套管约束全部自由度,油管下端约束竖直方向自由度,管柱的载荷与边界条件设定如图7所示。

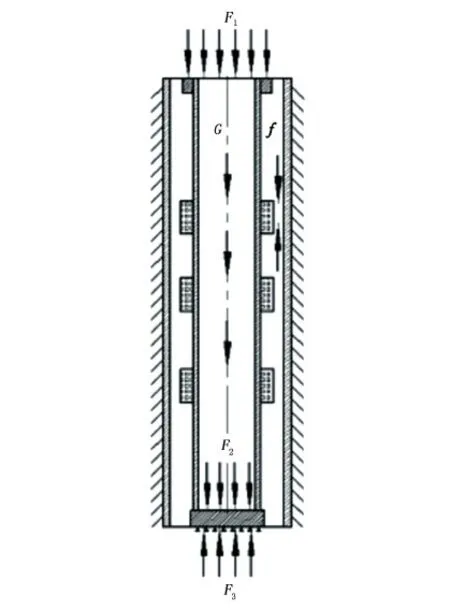
图7 载荷与边界条件Fig.7 Load and boundary condition

4.4 分析步定义与网格划分

完成对模型建立与载荷边界的设定后,须对模型的分析过程进行定义,由于本次分析中接触对较多,并且均为摩擦接触,故结合载荷特点选用结构静力分析(考虑几何大变形),求解方式采用迭代计算,并适当增大了不收敛时的迭代次数上限。定义完成后采用B31单元划分油管与套管的网格,提交运算。

4.5 数值分析结果

为了更好地观察管柱的变形情况,云图中将变形显示比例适当放大,图中发生屈曲的为油管,即管-管接触中的内管。由于丢手上方的管柱变形情况并非重点,且接触对越多,数值分析收敛难度越大,故有限元模型只对丢手接头及其以下的部分进行了建模。其中丢手至丝堵为建模时的正方向,故计算结果中位移的正值实际代表管柱的缩短。

图8为封隔器位移计算结果，图9为管柱屈曲位移云图。

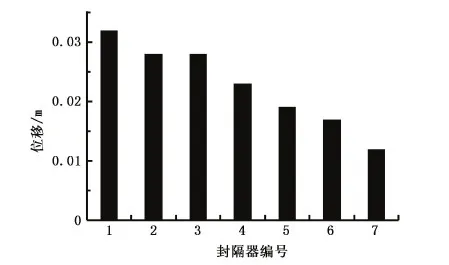
图8 封隔器位移计算结果Fig.8 Result of packers displacement

图9 管柱屈曲位移云图Fig.9 Tubes cloud chart about buckling

由图8、9所示可知:在理想状况下,分层采油管柱在支井底自由状态下,靠近井底部位的管柱将产生屈曲,封隔器下移,管柱的屈曲构型并非均匀螺旋线,而是正弦构型与不等距螺旋构型共同构成的复合屈曲构型,而且屈曲程度最低的区段恰好为7个封隔器所处位置附近,这是因为封隔器的主要元件为橡胶材质的胶筒,与套管之间摩擦系数远高于钢结构与套管之间的摩擦系数,这也说明了在考虑管柱与套管之间摩擦时,管柱的螺旋屈曲构型不再是均匀螺旋线。

4.6 误差分析

为了衡量封隔器位移计算结果的准确与否,将数值分析结果中封隔器位移与测井数据相比对如图10所示。

封隔器1、2、3、4、5、6、7的模拟偏差分别为6.7%、10.7%、16.7%、9.5%、5.6%、13.3%和9.1%。

现场磁定位数据的精准性受限于很多因素,本身存在一定偏差。

综上所述,虽然计算结果中最大误差达到16.7%,但误差来源较多,计算方法本身并不存在重大问题,而且数值分析结果趋势上与磁定位结果吻合,这证明使用文中建立的管-管摩擦接触模型对管柱井下受力变形情况进行数值模拟研究的方式是可行的,可以使用此方法进行井下工具串动后位置的预测。

图10 数值分析与磁定位结果对比Fig.10 Comparison of numerical analysis and magnetic positioning

5 结束语

建立了基于梁-梁接触理论的管柱摩擦接触有限元方法;在考虑摩擦的基础上进行了中33-P250井的管柱变形情况的数值分析,在存在摩擦的情况下管柱屈曲构型为复合不等距屈曲;对比了有限元分析结果与磁定位数据,验证了本文中提出的摩擦接触模型可用于管柱的屈曲分析与工具位置预测。

[1] 吕苗荣.石油工程管柱力学[M].北京:中国石化出版社,2012:12-16.

[2] 高德利.油气井管柱力学与工程[M].东营:中国石油大学出版社,2006:1-10.

[3] LIU J L, MEI Y, DONG X Q. Post-buckling behavior of a double-hinged rod under self-weight[J]. Acta Mechanica Solid Sinica, 2013,26(2):197-204.

[4] 李子丰,马兴瑞,黄文虎,等. 热采井套管柱力学分析[J]. 工程力学, 1998,15(2):19-26. LI Zifeng, MA Xingrui, HUANG Wenhu, et al. The mechanics analysis on thermal recovery wellscasing string[J]. Engineering Mechanics, 1998,15(2):19-26.

[5] LUBINSKI A. ALTHOUSE W S,LOGAN J L. Helical buckling of tubing sealed in packer [J]. Journal of Petroleum Technology, 1962,14(6):655-667.

[6] MITCHELL R F. Buckling behavior of well tubing: the packer effect[J]. SPE Journal, 1982,22(5):616-624.

[7] MITCHELL R F. New concept for helical buckling[J]. SPE Drill Engineering, 1988,3(3):303-310.

[8] MITCHELL R F. New buckling solutions for extended reach wells: the IADC/SPE Drilling Conference[C]. Dallas: Texas, 2002.

[9] MITCHELL R F. Tubing buckling—the state of the art[J]. SPE Drilling & Completion, 2008,23(4):361-370.

[10] 张绍槐,狄勤丰. 用旋转导向钻井系统钻大位移井[J]. 石油学报,2000,21(1): 76-80. ZHANG Shaohuai, DI Qinfeng. Petroleum engineering drilling extended reach well with rotary steering drilling system[J]. Acta Petrolei Sinica, 2000,21(1):76-80.

[11] 狄勤丰,王明杰,胡以宝,等. 柔性短节位置对带旋转导向工具底部钻具组合动力学特性的影响[J]. 中国石油大学学报(自然科学版), 2012,36(5):84-88. DI Qinfeng, WANG Mingjie, HU Yibao, et al. Effect of flex subs position on bottom hole assembly with rotary steering tool [J]. Journal of China University of Petroleum (Edition of Natural Science), 2012,36(5):84-88.

[12] 刘巨保,岳欠杯,等.石油钻采管柱力学[M]. 北京:石油工业出版社, 2011:78-132.

[13] 郭日修.弹性力学与张量分析[M]. 北京:高等教育出版社,2003:114-125.

[14] 邹德永,王家骏,卢明,等.定向钻井 PDC 钻头三维钻速预测方法[J].中国石油大学学报(自然科学版), 2015,39(5):82-88. ZOU Deyong, WANG Jiajun, LU Ming, et al. A novel prediction method of PDC bits ROP in directional drilling[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015,39(5):82-88.

[15] 井丽龙,张文平,明平剑,等.Timoshenko梁静力学和动力学问题有限体积法求解[J]. 哈尔滨工程大学学报, 2015,36(9):1217-1222,1275. JING Lilong, ZHANG Wenping, MING Pingjian, et al. Static and dynamic analysis of Timoshenko beam model on finite volume method [J]. Journal of Harbin Engineering University, 2015,36(9):1217-1222,1275.

[16] PRZEMYSLAW L. Finite element analysis of beam-to-beam contact [M]. India: Springer-Verlag Berlin Heidelberg,2010:1-22.

[17] Ds Simulia Corp. Abaqus 6.13 theory manual [M]. USA:Ds Simulia Corp, 2013.

[18] 车小玉,段梦兰,曾霞光,等. 双层管道整体屈曲实验研究及数值模拟 [J]. 应用数学和力学, 2014,35(2):188-201. CHE Xiaoyu, DUAN Menglan, ZENG Xiaguang, et al. Experimental study and numerical simulation of global buckling of pipe-in-pipe systems [J]. Applied Mathematics and Mechanics, 2014,35(2):188-201.

[19] KIRSTOFFERSEN A S, ASKLUND P O, NYSTR M P R. Pipe-in-pipe global buckling and trawl design on uneven seabed: proceedings of the 22nd International Offshore and Polar Engineering Conference[C].Greece: R Hodes, 2012:166-172.

[20] BOWDEN F P, TABOR D. The friction and lubrication of solids, part II [M]. Oxford:Clarendon Press, 1964:52-84.

(编辑 沈玉英)

Post-buckling analysis of tubes based on beam-to-beam contact theory

WANG Zunce1, CAO Mengyu1, XU Dekui2, WEN Houzhen1, XU Yan1, CHEN Ming1, LÜ Fengxia3

(1.MechanicalScientificandEngineeringCollegeofNortheastPetroleumUniversity,Daqing163318,China;2.CollegeofMechanicalEngineeringandAppliedElectronicsTechnology，BeijingUniversityofTechnology,Beijing100124,China;3.MechanicalEngineeringCollegeofChangzhouUniversity,Changzhou213016,China)

To explore the buckling form of the straight long tube under complicated conditions, the buckling analysis based on the beam-to-beam contact theory is carried out. The beam is discretized according to the beam-to-beam contact theory in consideration of shear and bending deformation. The finite element method(FEM) model considering the variable section and frictional contact is built, where the tube-to-tube contact element is used. By using this method, the FEM model concerned with the layered productions actual working conditions is presented. The result turns out that the tubes buckling form under the complex condition, is multiple and not equidistant. Moreover, the buckling form with friction is not the standard sine type or the spiral configuration, and the reliability of these results has been proved by the magnetic positioning data.

tube;tube-to-tube contact element; beam-to-beam contact theory; frictional contact; multiple buckling; magnetic positioning;subsurface tool

2016-03-12

国家青年科学基金项目(11402051)；东北石油大学研究生创新科研项目(YJSCX2016-021 NEPU)

王尊策(1962-), 男, 教授,博士,博士生导师,研究方向为石油流体机械及相关力学问题。E-mail:wangzc@nepu.edu.cn。

1673-5005(2017)02-0132-07

10.3969/j.issn.1673-5005.2017.02.016

O 343.9

A

王尊策,曹梦雨,徐德奎,等. 基于梁-梁接触理论的管柱屈曲分析[J]. 中国石油大学学报(自然科学版), 2017,41(2):132-138.

WANG Zunce, CAO Mengyu, XU Dekui, et al. Post-buckling analysis of tubes based on beam-to-beam contact theory [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(2):132-138.