基于裂纹尖端张开角含轴向穿透裂纹X80管道极限压力预测
曹宇光, 甄 莹, 贺娅娅, 张士华, 孙永泰, 衣海娇,刘 帆
(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.中国石油大学山东省油气储运安全重点实验室,山东青岛 266580; 3.机械结构强度与振动国家重点实验室,陕西西安 710049; 4.中国石化胜利石油工程有限公司钻井工艺研究院,山东东营 257055; 5.中国石油辽河油田分公司特种油开发公司,辽宁盘锦 124010)
基于裂纹尖端张开角含轴向穿透裂纹X80管道极限压力预测
曹宇光1,2,3, 甄 莹1,2,3, 贺娅娅1,2, 张士华4, 孙永泰3, 衣海娇1,2,3,刘 帆5
(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.中国石油大学山东省油气储运安全重点实验室,山东青岛 266580; 3.机械结构强度与振动国家重点实验室,陕西西安 710049; 4.中国石化胜利石油工程有限公司钻井工艺研究院,山东东营 257055; 5.中国石油辽河油田分公司特种油开发公司,辽宁盘锦 124010)
准确预测含轴向穿透裂纹管道极限压力对其安全运行具有重要意义,但现有极限压力预测模型已不满足高韧性、高强度X80管道的评定需求。对含轴向穿透裂纹X80管道极限压力进行研究,建立含轴向穿透裂纹X80管道壳单元与三维实体单元数值模型,应用壳单元模型替代三维实体单元模型以简化分析过程并提高计算效率。基于含裂纹管道壳单元模型,选用临界裂纹尖端张开角作为断裂参量,分析初始裂纹长度、检测单元长度、管道壁厚等不同因素对极限压力的影响,提出极限压力预测修正模型。将基于修正模型的管道爆破压力预测结果与试验测试结果进行对比分析。结果表明,初始裂纹长度与极限压力呈负相关关系;而检测单元长度和管道壁厚与极限压力呈正相关关系,且壁厚与极限压力基本呈近线性关系;三者均对极限压力具有较为显著的影响。该模型具有更高的准确性,可用于高韧性、高强度薄壁 X80 管道的止裂设计。
X80管道; 轴向穿透裂纹; 临界裂纹尖端张开角; 极限压力; 预测模型
在管道产业发展的过程中,提高管线钢钢级和输送压力已成为其强劲的发展趋势[1]。20世纪90年代以前,中国普遍采用A3、16Mn、TS52K等低强度焊管,输送压力大都在4 MPa以下;1993年,陕京管线首次采用X60 钢级,运输压力为6.4 MPa;2000年,西气东输一线管线采用X70钢级、10 MPa压力;2010年,西气东输二线干线全部采用X80 钢级,西段采用12 MPa 的设计压力,使中国管道建设上升到了新高度[2]。目前,X80管道在中国已得到广泛应用。X80管道韧性好,强度高,但仍不可避免地在生产、运输过程中形成缺陷或裂纹。管道裂纹存在形式多样,在对其评定时,通常会按照等应力强度因子的原则,将不同形式的缺陷用穿透裂纹代替。研究含轴向裂纹穿透管道极限压力并对其做出准确预测具有重要意义。基于X80管道高韧性、高强度的特点,其裂纹尖端存在明显的塑性区,超出了线弹性断裂力学小范围屈服条件要求,故需要一种新的弹塑性断裂准则来评估其剩余强度。裂纹尖端张开角(CTOA)作为裂纹尖端局部特性的一种表现,能较好地表征裂纹前沿应力应变状态。Andersson[3]首先将CTOA作为描述裂纹扩展的参数,Rizzi等[4]则将其用在石油管道运输领域,赵延广等[5]证明了CTOA在航空领域的适用性。冯耀荣等[6]将其应用在输气管线止裂预测中,帅健、陈福来等[7-8]分别对其进行了试验探究和有限元模拟,证明可通过有限元方法基于CTOA为油气管道的止裂设计提供依据。笔者针对含轴向穿透裂纹X80管道,基于弹塑性断裂力学方法,利用APDL参数化设计语言建立管道有限元模型,以临界CTOA作为裂纹扩展判据,确定其所能承受的极限压力,考察初始裂纹长度、检测单元长度、管道壁厚等因素的影响,最终建立起管道极限压力预测模型。
1 CTOA简介
CTOA即瞬时裂纹尖端张开角,目前其定义均基于试验测量结果,其中一个常用定义是将裂纹扩展后瞬时裂纹尖端与裂尖后距离为rm处上、下裂纹面上两对称点间连线所成夹角定义为瞬时裂纹尖端张开角,如图1所示,即[9]
CTOA=2arctan(δ/2rm).
(1)
式中,δ为裂尖后部一定距离处rm的裂尖张开位移。
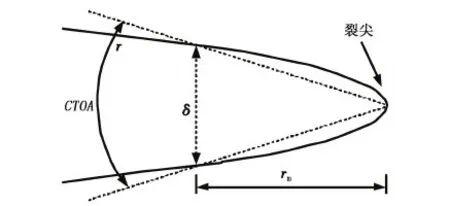
图1 裂纹尖端张开角定义Fig.1 Definition of crack tip opening angle(CTOA)
rm对CTOA值有较大影响,但具体应取在何处,目前尚无统一标准[10]。在试验中通常取rm为1 mm[11]。在有限元计算中CTOA根据裂纹尖端后面节点的位移进行计算[12]。将计算CTOA时所使用的节点到裂尖之间的距离称为检测单元长度。
理论与试验证明,对于含有初始裂纹的管道,当外力不断增加时,其裂纹对应的CTOA亦随之增加,当CTOA达到某一临界值时,即使外力不再增加,裂纹也会急剧地高速扩展。其临界值记为CTOAC,定义如下[13]:
(2)
式中,δt为裂尖真实张开位移;Δa为裂纹扩展量。
CTOAmax=CTOAC.
(3)
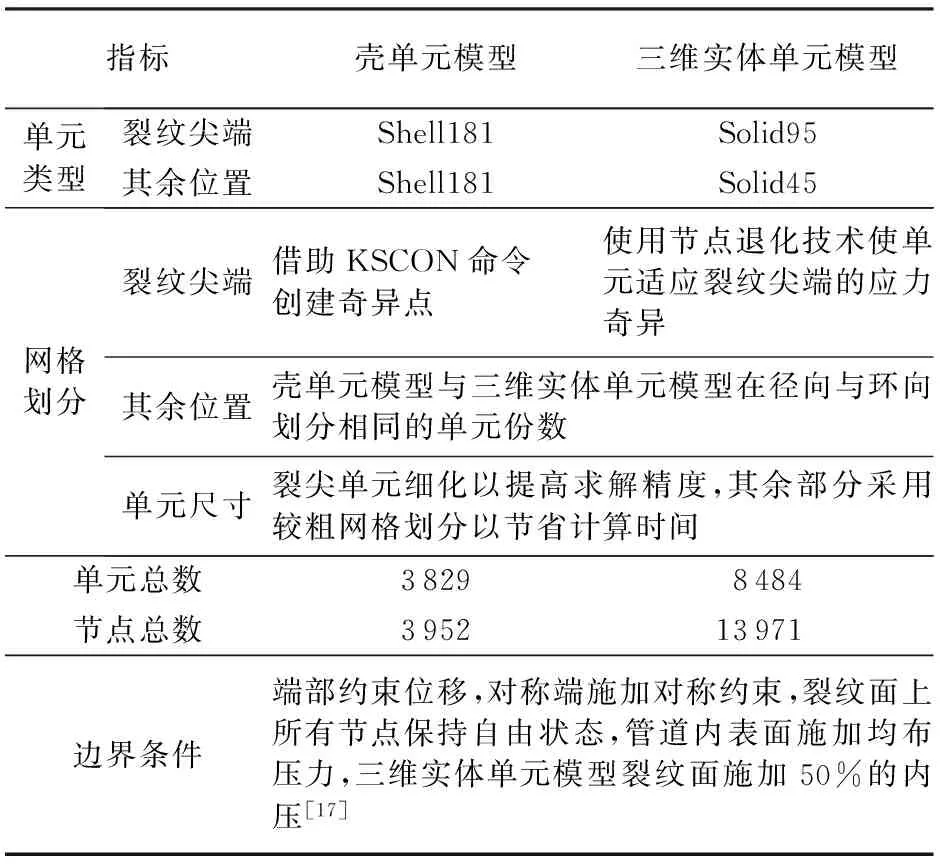
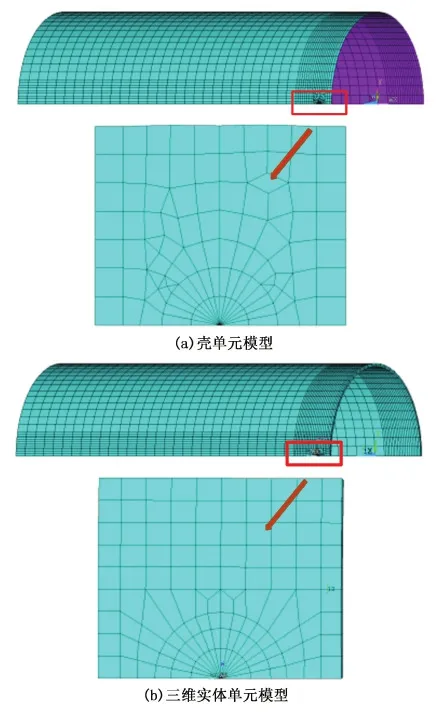
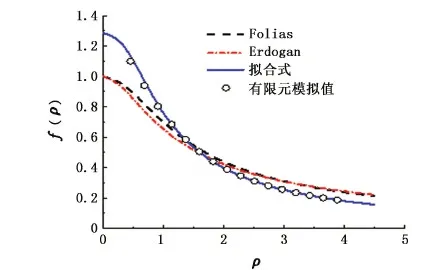
这是评估裂纹扩展的CTOA准则。即当CTOAmax>CTOAC时,裂纹将失去平衡而失稳扩展;若CTOAmax CTOA的获得一般可通过试验和有限元模拟两种方式。为了满足薄壁结构的断裂韧性测试需要,国际标准化组织(ISO)和美国材料与试验协会(ASTM)先后发布了测试标准ISO 22889和ASTM E2472,明确了稳态裂纹扩展过程中CTOA的测试方法[15]。CTOA的测试对试验设备以及操作人员均提出了较高要求,加上裂纹扩展的不确定性往往导致难以获得准确结果。鉴于有限元方法的有效性,工程实践中常将其作为重要的CTOA测试手段。在对含裂纹薄壁管道进行CTOA有限元模拟时,壳单元模型与三维实体单元模型均有应用[8,16]。本文中同时建立壳单元模型与三维实体单元有限元模型,并对结果进行对比,从而确定优选的模型。 2.1 有限元模型 针对含轴向穿透裂纹X80管道,分别建立壳单元模型与三维实体单元模型,模型基本设置如表1(管道直径为1 016 mm,壁厚为15.3 mm,初始半裂纹长度为80 mm,E=206 GPa,μ=0.3)所示。 两者的差异主要在于单元选择和裂纹尖端的处理方式上:壳单元模型选用弹塑性壳单元Shell181,三维实体单元模型选用改进的20节点Solid95实体单元构造裂纹尖端,其余位置选用Solid45。与三维实体单元模型相比,壳单元模型单元总数不足其一半,而节点总数仅为其四分之一,可见在计算时间及所占内存等方面,壳单元模型要优于三维实体单元模型。 在进行裂尖处理时,壳单元模型可直接借助KSCON命令创建奇异点,而三维实体单元模型则须使用节点退化技术处理裂尖单元,即将裂纹尖端单元中间节点移至1/4节点位置处以使其适应该处的应力奇异,可见壳单元建模难度明显小于三维实体单元建模[18]。裂纹尖端及附近的有限元模型如图2所示。 表1 含轴向穿透裂纹X80管道壳单元模型与三维实体单元模型对比Table 1 Comparison of shell element model and three-dimensional solid element model of X80 pipeline with axial through-wall crack 图2 含轴向穿透裂纹X80管道有限元模型Fig.2 Finite element model of X80 pipeline with axial through-wall crack 2.2 CTOA计算 考虑到管道实际受载情况,由于裂尖塑性区较大,需要对其进行弹塑性分析。本文设定材料为多线性率无关各向同性,应力应变关系来自于拉伸试验[19]。 从人口状况来看,目前竹农家庭以3~4人为主,占调查总户数的51.1%,平均每户人口为3.96人;人口在5人及其以上的农户占39.8%。从经营者年龄上看,被调查者的平均年龄为57.3岁,最大者为84岁,最小者为33岁;其中51~60岁者竹农占47.9%,61~70岁者占35.1%,71岁以上者占6.4%,50岁以下的竹农仅占10.6%。可见,大部分竹林经营者都是爷爷、奶奶辈,劳动者趋于老龄化;而且竹林经营面积越小,经营者的年龄越大。说明现有的竹林经营规模无法吸引年轻人。 对两种模型均施加内压10 MPa,提交运算,可得到图3所示的裂纹尖端应力分布云图。由图3可以看出,在同等工况下两种模型所得应力分布情况相似,最大应力均出现在裂纹尖端附近,且其值仅相差3.11%。观察塑性区的形状可知,不同模型对其影响也不大,进一步计算可得两种模型塑性区半径分别为0.041和0.041 5 m,壳单元模型所得塑性变形区域略小于三维实体单元模型,但差距仅为1.2%。同时,在载荷及边界条件作用下,可以看到裂纹自由面张开,选取一定的检测单元长度,利用节点位移并结合相关几何关系进行CTOA的计算,可得到该工况下两种模型对应的CTOA值分别为2.91°与3.01°,二者相差甚微。综上可知,在模拟含轴向穿透裂纹X80管道应力分布及CTOA时,壳单元模型与三维实体单元模型具有较好的一致性。 图3 Von Mises应力分布Fig.3 Distribution of Von Mises stress 通过对CTOA的模拟可知,对于含有初始轴向穿透裂纹的管道,当内压不断增加时,CTOA亦随之增加,直至达到临界值,此后裂纹将失稳扩展,管道失去承载能力,与之对应的内压即为管道极限压力。通过文献调研[7]可知,CTOA临界值受试件韧带厚度及约束条件等因素的影响,但对于X80管道,其范围一般在7.8°~12.8°。综合考虑,本文中取临界CTOA为11.2°。 3.1 不同模型对极限压力影响 前文分别对比了壳单元模型与三维实体单元模型在模拟精度、应力分布及CTOA计算时的区别,结果均表明,两者具有较好的一致性。 以西气东输工程中直径为1 016 mm、壁厚为15.3 mm与直径为1 219 mm、壁厚为18.4 mm的管道为例,对其在不同初始裂纹长度下的极限压力进行对比分析,所得极限压力(pC)随初始裂纹长度变化见图4。 图4 不同直径管道极限压力随初始裂纹长度变化Fig.4 Limit pressure of different diameter pipes under different initial crack length 由图4可知,对于具有相同尺寸与初始裂纹长度的管道,壳单元模型与三维实体单元模型所得极限压力相近:直径为1 016 mm时,两者最大相差为3.36%;直径为1 219 mm时,两者最大相差为4.21%。同时,随初始裂纹长度增加,二者所得极限压力趋于相同。考虑到壳单元模型在建模难度和计算速度等方面的优越性,采用壳单元模型进行含轴向穿透裂纹X80管道极限压力预测模型研究。 3.2 初始裂纹长度对极限压力影响 由图4可以发现,不同尺寸管道极限压力随初始裂纹长度变化规律一致,即初始裂纹长度越大,对应的极限压力越小,且随初始裂纹长度增加,极限压力的变化逐渐趋于平缓。这是由于初始裂纹长度通过影响管道韧带长度而影响管道的断裂韧性,在初始裂纹长度较小时,管道承载能力较大,断裂韧性受初始裂纹长度影响明显,因此极限压力随初始裂纹长度增大而明显减小;但随初始裂纹长度增加,管道承载能力降低到一定程度,即使很小的内压都可以使管道发生失效,所以极限压力逐渐趋于定值。 3.3 检测单元长度对极限压力影响 利用壳单元建立直径为1 016 mm、壁厚为15.3 mm、初始半裂纹长度分别为80、160、300 mm的X80管道模型。图5为两种模型下不同检测单元长度对极限压力的影响。 图5 不同检测单元长度对极限压力影响Fig.5 Effects of test element length on limit pressure 从图5可以看出,同一工况下,选取不同检测单元长度会得到不同极限压力,随检测单元长度增大,不同初始裂纹长度下的极限压力均呈增大趋势。当检测单元长度小于5 mm时,极限压力增大趋势明显,之后增大趋势减弱,当检测单元足够大时,极限压力将逐渐收敛。 由于检测单元长度对极限压力具有较大的影响,在有限元模拟中须以爆破试验和已知的模拟结果为依据,不断调整模型及参数,直至模拟结果与试验结果吻合。确定的检测单元长度为15 mm[20]。 3.4 管道壁厚对极限压力影响 在利用壳单元建立管道模型时,无须考虑壁厚单元划分的作用,但仍须考虑壁厚尺寸对极限压力的影响。以直径1 016 mm、壁厚15.3 mm,初始半裂纹长度分别为80、160、300 mm的X80管道模型为例,研究极限压力随管道壁厚的变化(图6)。 从图6可以看出,在不同初始裂纹长度下,管道极限压力均与壁厚呈近线性关系,管道壁厚越大,对应的极限压力也越大。这是由于壁厚影响了裂纹尖端的约束情况,在一定范围内,约束会随管道厚度增大而逐渐增加,因此裂纹扩展需要的压力也随之增大。 图6 不同管道壁厚对极限压力影响Fig.6 Effects of pipeline thickness on limit pressure 4.1 极限压力预测模型 现有模型基本遵循的形式[21]为 (4) Folias[22]基于Tresca屈服准则对试验结果进行了统计并结合线弹性断裂力学理论建立的极限压力预测模型为 (5) 基于应力强度因子K,Erdogan[23]推导得到 (6) 而Kim等[17]基于Mises屈服条件,利用理想弹塑性有限元模型对含轴向穿透裂纹X80管道极限压力进行研究,得到 (7) 3种预测模型对比如图7所示。由图7可以看出,Folias式与Erdogan式结果较为接近,而在ρ<1 时,式(7)的计算结果大于前二者。前二者均为20世纪70年代提出,其研究对象为壁厚较大的核工业压力管道,但对于高强度、高韧性的现代薄壁管道,其适用性有待进一步研究。Kim式则是对承受内压的一定长度闭合管段进行有限元分析得到,这与长输管道的实际作业工况并不完全一致。 图7 3种极限压力预测模型对比Fig.7 Comparison of three prediction models for limit pressure (8) 图8为极限压力预测模型对比。 图8 极限压力预测模型对比Fig.8 Comparison of the limit pressure prediction models 如图8所示,该预测模型能准确反映有限元数值模拟结果,两者最大相差仅为6.49%。在此基础上,将本文模型与Folias和 Erdogan模型进行对比可以发现:当ρ<1.5时,本文的预测结果较大;当ρ>1.5时,本文的预测结果较小;在ρ=1.5附近,三者基本相等。究其原因:当ρ<1.5时,管道裂纹长度较小,高韧性的X80管道材料须吸收更多的能量裂纹才能进一步扩展,因此本文中预测的极限压力较基于韧性较低的管道材料预测模型为大;随着ρ增大,管道裂纹长度增加,其所能承受的极限压力逐渐降低,且减小幅度趋于平缓,此时,管道壁厚对抵抗裂纹扩展起主要作用,因此本文中预测的X80管道极限压力较基于核工业厚壁管道所建立模型预测结果为小。 4.2 管道爆破试验数据验证 根据某厂生产的4种不同规格的X80钢管的水压爆破试验实测数据[24],对所提出的预测模型进行分析验证。试验管道的相关参数及其爆破压力测试结果如表2所示。基于不同预测模型所得到的爆破压力及其与测试结果的误差总结如表3所示。须指出的是,爆破试验管道并未预制裂纹,而各预测模型均针对含轴向裂纹管道,因此在计算极限压力时取ρ=0。 表2 试验管道相关参数Table 2 Parameters of tested pipelines 从表3可以看出,基于Folias与Erdogan预测模型得到的爆破压力相同,均小于试验值,最大误差为16.55%,而基于本文预测模型所得结果则略大于试验测试值,最大误差为12.81%。这与图8所显示的当ρ<1.5时本文中预测结果较大是一致的。虽然本文中极限压力预测公式存在一定高估误差,但总体上来说,对含轴向穿透裂纹高韧性的X80薄壁管道,提出的极限压力预测精度更高。 表3 爆破压力与预测压力对比Table 3 Comparison of burst pressures by tests and prediction 综上所述,以临界CTOA为依据进行管道极限压力预测是可行的,由此所得到的极限压力预测模型可用于工程实践,具有较高的准确性。 (1)内压作用下含轴向穿透裂纹X80管道壳单元模型与三维实体单元模型的应力分布情况相似,等效应力最大值接近且均出现在裂纹尖端附近;塑性区的形状接近,壳单元模型所得塑性区半径略小于三维实体单元模型,但差距仅为1.2%;同等条件下计算所得CTOA值基本一致;基于材料临界CTOA所确定的管道极限压力相差小于5%。同时,壳单元模型在建模难度、所占内存、运行时间等方面远优于三维实体单元模型。 (2)初始裂纹长度与极限压力呈负相关关系;而检测单元长度和管道壁厚与极限压力呈正相关关系,且壁厚与极限压力基本呈近线性关系;三者均对极限压力具有较为显著的影响。新模型具有更高的预测精度。 [1] 李鹤林,吉玲康,田伟.高钢级钢管和高压输送:我国油气输送管道的重大技术进步[J].中国工程科学,2010,12(5):84-90. LI Helin, JI Lingkang, TIAN Wei. High steel pipe and high pressure transmission: the major technical progress of Chinas oil and gas transmission pipeline [J]. Engineering Sciences, 2010,12(5):84-90. [2] 李鹤林,吉玲康,田伟.西气东输一、二线管道工程的几项重大技术进步[J].天然气工业,2010,30(4):1-9. LI Helin, JI Lingkang, TIAN Wei. Several major technical progress of the west east gas pipeline project [J]. Natural Gas Industry, 2010,30(4):1-9. [3] ANDERSSON H. A finite-element representation of stable crack-growth [J]. Journal of the Mechanics and Physics of Solids, 1973,21(5):337-356. [4] DEMOFONTI G, RIZZI L. Experimental evaluation of CTOA in controlling unstable ductile fracture propagation: Defect Assessment in Components—Fundamentals and Applications, SEIS/EGF 9[C]. London: Engng,2013. [5] 赵延广,刘建中,胡本润,等.薄壁结构剩余强度预测方法研究进展[J].理化检验(物理分册),2015,51(8):525-534. ZHAO Yanguang, LIU Jianzhong, HU Benrun, et al. Research progress on residual strength prediction of thin-walled structures [J]. Physical Testing and Chemical Analysis(Part A:Physical Testing), 2015,51(8):525-534. [6] 冯耀荣,庄茁,庄传晶,等.裂纹尖端张开角及在输气管线止裂预测中的应用[J].石油学报,2003,24(4):99-107. FENG Yaorong, ZHUANG Zhuo, ZHUANG Chuanjing, et al. Crack tip opening angle and its application to crack arrest in gas pipeline [J]. Acta Petrolei Sinica, 2003,24(4):99-107. [7] 陈福来,帅健,祝宝利.X80管道钢裂纹尖端张开角的试验研究[J].压力容器,2010,27(10):8-11. CHEN Fulai, SHUAI Jian, ZHU Baoli. Experimental investigation on crack tip opening angle of X80 pipeline steel [J]. Pressure Vessel Technology, 2010,27(10):8-11. [8] 帅健,张宏,王永岗,等.输气管道裂纹动态扩展及止裂技术研究进展[J].石油大学学报(自然科学版),2004,28(3):129-135. SHUAI Jian, ZHANG Hong, WANG Yonggang, et al. Research advance of dynamic crack propagation and arrest techniques for gas transmission pipeline [J]. The University of Petroleumm,China(Edition of Natural Science), 2004,28(3):129-135. [9] KANNINEN M F, LEUNG C P, O' DONOGHUE P E, et al. Joint final report on the development of a ductile pipe fracture model [R]. Arlington, Virginia: Pipeline Research Committee, American Gas Association, 1992:37-44. [10] 赵忠庆,王生楠,茅佳兵.基于CTOAC评估结构断裂特性的方法研究[J].航空计算技术,2012,42(2):77-80. ZHAO Zhongqing, WANG Shengnan, MAO Jiabing. Research on assessment of fracture for damaged structures based on CTOAC[J]. Aeronautical Computing Technique, 2012,42(2):77-80. [11] SHTERENLINKHT A, HASHEMI S H, Howard I C,et al. A specimen for studying the resistance to ductile crack propagation in pipes [J]. Engineering Fracture Mechanics, 2004,71(13/14):1997-2013. [12] 帅健,张宏,许葵.输气管道裂纹动态扩展的数值模拟[J].油气储运,2004,23(8):5-8. SHUAI Jian, ZHANG Hong, XU Kui. Numerical simulation of crack propagation in gas transmission pipeline [J]. Oil & Gas Storage and Transportation, 2004,23(8):5-8. [13] DEMOFONTI G, BUZZICHELLI G, VENZI S, et al. Step by step procedure for the two specimen CTOA test [J]. Pipeline Technology, 1995,2:503-512. [14] MARTINELLI A, VENZI S. Tearing modulus, J-integral, CTOA and crack profile shape obtained from the load-displacement curve only [J]. Engineering Fracture Mechanics, 1996,53(2):263-277. [15] 韩克江,帅健,王俊强,等.管道大范围屈服断裂评估的研究现状与进展[J].力学进展,2012,42(1):29-40. HAN Kejiang, SHUAI Jian, WANG Junqiang, et al. Research status and development of large scale yield and fracture assessment of pipeline [J]. Advances in Mechanics, 2012,42(1):29-40. [16] 赵耀.关于裂纹柱壳韧性断裂的研究[J].海洋工程,1999,17(2):10-16. ZHAO Yao. Study of ductile fracture of circumferential through-wall cracked cylinders [J]. The Ocean Engineering, 1999,17(2):10-16. [17] KIM Yunjae, SHIM Dojun, HUH Namsu. Plastic limit pressures for cracked pipes using finite element limit analyses [J]. International Journal of Pressure Vessels and Piping, 2002,79(5):312-330. [18] 张朝晖.ANSYS 11.0结构分析工程应用实例解析[M].北京:机械工业出版社,2008. [19] 王玲,贾普荣,李年,等.单轴载荷下X80钢的包申格效应研究[J].试验力学,2005,20(3):423-426. WANG Ling, JIA Purong, LI Nian, et al. Study on Bauschinger effect of X80 steel under uniaxial load [J]. Journal of Experimental Mechanics, 2005,20(3):423-426. [20] 李红克,张彦华.以临界CTOA为参量的含裂纹管道极限压力有限元模拟[J].焊接学报,2005,26(1):53-58. LI Hongke, ZHANG Yanhua. Finite element simulation of the limit pressure of a cracked pipe with the critical CTOA as the parameter [J]. Transactions of the China Welding Institution, 2005,26(1):53-58. [21] MILLER A G. Review of limit loads of structures containing defects [J]. International Journal of Pressure Vessels and Piping, 1988,32(1):197-327. [22] FOLIAS E S. On the fracture of nuclear reactor tubes: 3rd Int Conference on SMiRT[C]. London: UK,1975. [23] ERDOGAN F. Ductile failure theories for pressurized pipes and containers [J]. International Journal of Pressure Vessels and Piping, 1976,4(4):253-283. [24] 王鹏,刘迎来,池强,等.X80感应加热弯管爆破试验分析研究[J].热加工工艺,2010,39(24):257-259. WANG Peng, LIU Yinglai, CHI Qiang, et al. Research on burst pressure of X80 induction bends[J]. Hot Working Technology, 2010, 39 (24): 257-259. (编辑 沈玉英) Prediction of limit pressure in axial through-wall cracked X80 pipeline based on critical crack-tip opening angle CAO Yuguang1,2,3, ZHEN Ying1,2,3, HE Yaya1,2, ZHANG Shihua4, SUN Yongtai3, YI Haijiao1,2,3, LIU Fan5 How to accurately predict the limit pressure of the pipeline with axial through-wall cracks is of great significance to its safety working conditions. However, the existing limit pressure prediction models cant meet the requirements of X80 pipelines which are of high toughness and high strength. Considering this feature, the limit pressure of X80 pipeline with axial through-wall cracks is studied in this paper. Firstly, both of the shell element and three-dimensional solid element are used in the modeling process. The shell element model is chosen to displace the three-dimensional element model for analysis, in order to simplify the calculation and improve the computational efficiency. Based on the shell element model, the critical crack-tip opening angle (CTOA) is selected as the fracture criterion, and the effects of different factors such as the initial crack length, length of finite element, pipe wall thickness, are discussed. Finally, a modified model for the prediction of limit pressure is proposed. The burst pressure of pipelines predicted by the modified model is compared with that from the experimental results. The results show that there was a negative correlation between the initial crack length and the limit pressure, while the test element length and the wall thickness of the pipe were positively correlated with the limit pressure. What is more, the wall thickness is nearly linear with the limit pressure. And all of the three factors have a significant effect. The proposed model is more accurate than the existing one, and it can be used in the crack arrest design of thin-wall X80 pipes with high toughness and high strength. X80 pipeline; axial through-wall crack; critical crack-tip opening angle; limit pressure; prediction model 2016-03-22 国家自然科学基金项目(11472309);国家重点研发计划项目(2016YFC0802306);中央高校基本科研业务资助项目(14CX02208A);国家重点实验室开放课题(SV2017-KF-02) 曹宇光(1979-),男,教授,博士,博士生导师,研究方向为海洋工程技术、管道完整性、断裂失效与断口分析等。E-mail:caoyuguang@gmail.com。 1673-5005(2017)02-0139-08 10.3969/j.issn.1673-5005.2017.02.017 TE 88 A 曹宇光,甄莹,贺娅娅,等. 基于裂纹尖端张开角含轴向穿透裂纹X80管道极限压力预测[J]. 中国石油大学学报(自然科学版), 2017,41(2):139-146. CAO Yuguang, ZHEN Ying, HE Yaya, et al. Prediction of limit pressure in axial through-wall cracked X80 pipeline based on critical crack-tip opening angle[J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(2):139-146.2 含轴向穿透裂纹X80管道的CTOA数值模拟

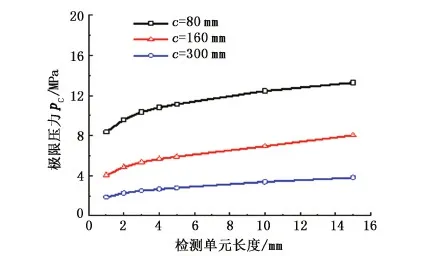
3 含轴向穿透裂纹X80管道极限压力分析


4 极限压力预测模型分析与验证



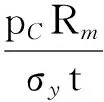


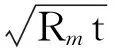



5 结 论


