量化概念格上网络盗窃行为拟合预测

王 慧, 秦 静, 郑 涛

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

量化概念格上网络盗窃行为拟合预测

王 慧, 秦 静, 郑 涛

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

时间序列挖掘是在经典的数据关联分析过程中加入时间戳印记，从而发现一定时间间隔内事物对象不同行为模式之间的关联关系。网络盗窃是一针对不特定多数人实施的短期多发性犯罪活动，其原始数据记录形式为多属性关联信息表，数据分布因具有时间顺序特征而符合时间序列挖掘分析的基本条件，为对该类数据进行频繁序列模式提取。首先论述了建立量化概念格数学模型的知识表示优势，证明了该格结构对原始数据表的完备性，其次提出了量化概念格上的频繁序列生成算法AMSP，最后在网络盗窃行为的拟合分析中对AMSP算法加以验证，说明该算法对于时间序列分析具有直观高效性，同样可应用于与网络盗窃案件具有相似数据特征的其他网络犯罪行为的预测分析。

网络盗窃; 概念格; 序列挖掘; 关联规则

0 引言

伴随着网络经济的迅速崛起，个人网络交易数量急剧增长，网络交易安全倍受关注，由于个人财产在网络空间主要体现为电子资金、网络服务、虚拟物品等电子数据形式，网络盗窃案件的犯罪对象也集中于这些具有价值属性的电子数据，侵害对象围绕不特定多数群体，与传统盗窃相比，网络盗窃犯罪的涉案总金额大，社会影响极其恶劣。网络盗窃是指采取非正当手段在网络空间将他人有形或无形财物据为己有的行为[1]，网络为其获利来源，网络盗窃具有跨地域性、侵犯对象随机性、犯罪实施短期性等特点，但其发生发展的时间规律性较强，在案件涉及的人、地、物、事件、组织5要素中，网络盗窃案件的地域环节对案件的影响极大减弱，而物、组织、事件环节均存在于网络环境，其中组织、事件属性的主要特征均具有时间印记，涉案人员常在短期内多次连锁盗窃，作案手段时间规律性强，因此，在案件侦破、证据链梳理过程进行时间序列预测， 寻找网络盗窃行为之间的高频度犯罪特征模式，可为案件的取证侦查工作提供新的思路。

时间序列分析是围绕历史行为的客观记录预测未来活动的数据处理方法，在事务数据库中挖掘频繁序列模式的目的在于发现研究对象在某段时间内的行为变化规律[2]，揭示研究对象在某段时间间隔内具有行为X之后与实施行为Y的关联程度[3]，序列分析是关联规则与时间维度的结合体，以事务数据库为基础建立序列分析数学模型是关键[4]。为了发现事物之间及属性之间的时间关联性，引入量化概念格数学模型，完备的量化概念格可以完整体现事务数据库的基本特征，由量化概念集所导出的子集偏序关系可形成Hasse图，基于Hasse图的频繁时间序列发掘更加简洁直观。网络盗窃案件的原始数据记录形式为多属性关联信息表，案件在信息表中以事物对象形式出现，案件基本特征表现为属性，同一涉案人员的多次盗窃活动在信息表中已经按照案发时间顺序记录，数据记录格式具备时间序列分析的基本条件。对网络盗窃犯罪行为进行时间序列挖掘可从微观上展现作案过程的基本特征、电子证据的分布特点等规律，对于网络盗窃案件的侦破工作具有实际意义。

1 量化概念格的知识表示形式

概念格由德国数学家Rudolf Wille于1982年提出[5]，该格结构是事务数据库中对象与属性之间二元关系所建立的层次概念结构，格中每一概念均由外延与内涵组成，描述了对象与属性之间的联系。概念格定义于给定的形式背景之上，设给定形式背景表示为T=(D,A,R)，其中D={x1,x2,…xn}为描述对象集合；A={a1,a2,…am}为属性集合；R为D和A之间的二元关系，R⊆D×A，其中若〈x,a〉∈R，则称x具有属性a，若〈x,a〉∉R，则称x不具有属性a。若在形式背景T上定义如下运算：

X*={a|a∈A,∀x∈X,〈x,a〉∈R}
Y*={x|x∈D,∀a∈Y,〈x,a〉∈R}

其中，X⊆D，Y⊆A，则X*表示对象集X中所有对象具有的共同属性集合，Y*表示具有Y中所有属性的对象集合，此时形式背景T的知识表示形式与数据信息表一致，而信息表是进行时间序列分析的基础。

定义1 设T=(D,A,R)为给定形式背景，二元组〈X,Y〉满足X*=Y且X=Y*，则称C〈X,Y〉为一概念，其中X为概念的外延，Y为概念的内涵。该形式背景下全体概念形成概念格，也称为Galois格，记为L(D,A,R)[6]。

定义2 设C〈X,Y〉为一概念，称C′〈|X|,Y〉为真实概念C所对应的量化概念，其中|X|为外延的基数，由量化概念所构成的格称为量化概念格[6]。

定理1 形式背景T=(D,A,R)下的概念格为一完备格。

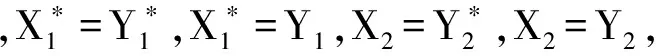
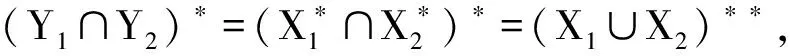
定理2 量化概念格与其所对应的真实概念格同构且具有完备性。

证明：由定义2可知，量化概念格与其对应的真实概念格属于同一形式背景，设C1〈X1,Y1〉、C2〈X2,Y2〉为该形式背景T=(D,A,R)下任意真实概念，C′1〈|X1|,Y1〉、C′2〈|X2|,Y2〉为其对应量化概念，由定理1知，X1⊆X2⟺Y2⊆Y1，所以C1≤C2，该形式背景下所定义的偏序关系可以只根据概念内涵间的子集关系确定而不会改变原格结构，将概念的外延量化并不影响同一形式背景下概念格的结构，所以量化概念格与其所对应的真实概念格同构，量化概念间的关系取决于与其对应真实概念间的关系：C′1≤C′2当且仅当C1≤C2。又因为全量化概念〈|D|,∅〉与空量化概念〈0,A〉属于该格结构，所以量化概念格为一完备格。证毕。

由上述证明可知，概念格可以体现数据信息表的全部内容，同一形式背景下的量化概念格与其对应的真实概念格同构且包含了时间序列分析所需的支持度计数值，针对数据信息表的时间序列关联分析可在量化概念格结构上进行，其格结构的完备性可保证数据信息量的完整性。

2 时间序列挖掘与概念格之间的关系

时间序列挖掘分析的目的在于发现事物数据库中描述对象在不同时间戳下的频繁行为模式，设事物数据库D={t1,t2,…,tn}，每一事物ti由标识符tid与属性子集Ai表示，Ai⊆A，其中属性集A={a1,a2,…,am}为所有属性值的集合，时间序列挖掘就是以事物数据库为依托在给定支持度约束下寻找属性子集的有序列表[7]，该列表与时间维度相关。鉴于概念格简洁完备的知识表示结构，形式背景之上偏序关系所对应格结构的存在使得概念之间的包含关系可以用Hasse图直观表示，概念格L(D,A,R)中各概念间的关系体现在Hasse图层间结点的连接关系。在支持度阈值约束下，属性集上序列模式的发现问题可表达为Hasse图中内涵上以外延基数为约束的子树序列发现问题。

对于给定的事务数据库，常规关联规则挖掘问题是寻找在属性A出现的条件之下属性B出现的可能性，而序列挖掘在事务数据库所形成的序列数据库上进行，在序列数据库中寻找高频次出现的序列模式，该序列由若干子序列构成，子序列是若干属性值的集合。依据用户给定的最小支持度将满足支持度阈值限制的序列称为频繁序列，也称该序列为一序列模式，是关联规则挖掘中的频繁属性集列表[7]。序列模式挖掘的形式化描述如下：

定义3[8]设序列S={S1,S2,…,Sn}，元素Si为属性子集Ai，序列所包含的所有属性值的个数称为序列的长度。序列S在序列数据集D上的支持度(Support)是D中包含S的序列个数，即，

简记为sup(S)，由用户指定的最小支持度称为序列S的支持度阈值。

定义4 序列S={S1,S2,…,Sn}是序列T={T1,T2,…,Tm}(n≤m)的子序列指对于任意整数i≤n，总存在j≤m使得Si⊆Tj，记为S⊆T。

序列模式挖掘过程中的序列子集是属性集合，表示某一事务中属性序列的出现状况，当事务数据库D所包含的属性均为二值属性时，属性集即属性值的集合。在序列模式生成过程中，对于给定的支持度阈值ζ，若sup(S)≥ζ，则该序列为频繁序列，实际挖掘过程更关注最大频繁序列，根据序列空间理论，频繁序列的子集仍然是频繁序列。由于序列的支持度计数值直接影响频繁序列的生成，体现在量化概念格中的结点C′〈|X|,Y〉的量化外延，这种通过对概念外延的量化表示获得的量化概念形式更简洁，更便于支持度计算，更有利于直观地进行序列模式挖掘。

3 量化概念格上的频繁序列生成算法AMSP

鉴于量化概念格直观的知识表示形式及其与序列模式生成过程的紧密联系，根据最小支持度阈值可直接生成所有频繁量化概念并以Hasse图形式输出，图中包含所有频繁序列集，由于在频繁序列集生成过程中去除了原有序列数据库对应概念格中的非频繁概念，因此频繁量化序列集所对应的Hasse图已不是完全意义上的格结构，仅保留其偏序特性[9]。

考虑概念格上子集偏序关系本身的次序性，在序列数据库所对应的量化概念格Hasse图中，序列模式为Hasse图中外延基数大于支持度阈值的结点内涵。量化概念格上的频繁序列生成算法AMSP(the Algorithm Mining Sequential Pattern based on the Concept Lattice Quantified)如下：

输入：事物数据集D及支持度阈值ζ

输出：序列模式集Smax

步骤1：对事务数据集D以事物标识tid为主要关键词以事物发生时间为次要关键词排序，将事务数据库转化为序列数据库C；

步骤2：创建Hasse图的L0层结点Root，标记为〈|C|,∅〉，根据支持度阈值ζ扫描序列数据库C，获得长度为1的频繁子序列L1，将L1作为初始种子集Seed；记录包含L1的序列数|X|，并按|X|值降序排列，生成Hasse图的第1层；

步骤3：i=1；

步骤4：根据Li，通过连接与剪枝运算形成候选序列Si+1，扫描序列数据库C，计算sup(Si+1)，产生长度为i+1的频繁子序列Li+1，形成Hasse图的第i+1层，更新种子集Seed，若种子集无变化转向步骤6；

步骤5：i=i+1，转向步骤4；

∥步骤4形成Hasse图的Lj(j>1)层

步骤6：为相邻层间具有遮盖关系的结点连边并输出叶子结点的外延集。

根据AMSP算法，序列模式的发现是在经典关联规则提取过程中加入时间维度，为提取最大序列，频繁子序列集生成过程融剪枝策略于一体，选取表1所示数据库验证AMSP算法的执行过程。

表1 示例数据库

在表1中，事物tid已经按照时间顺序排列，因此可忽略事物发生的时间戳，将事物tid相同的记录合并后，可得表2所示的序列数据库。

表2 序列数据库

设给定最小支持度阈值为2时，示例数据库所对应的频繁量化序列Hasse图如图1所示。

图1 示例数据库的频繁量化序列Hasse图

由图1可知，当给定支持度阈值为2时，序列(ACD)、(BCD)为最大频繁序列，所包含子序列都是重要属性值。

4 量化概念格上网络盗窃行为拟合预测

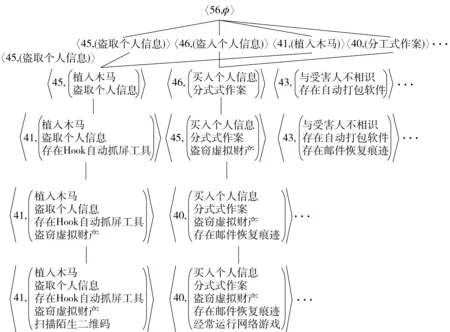
图2 网络盗窃行为所生成频繁概念集上的Hasse图

网络盗窃案件的立案依据主要是刑法的二百六十四条[1]，立案标准参照最高人民法院及最高人民检察院关于盗窃刑事案件的相关解释，其中盗窃价值1 000至3 000元以上的公私财物已属于刑法二百六十四条规定的“数额较大”环节，而网络盗窃犯罪是在一定时间阶段爆发的多次盗窃活动，涉案金额往往在“数额较大”环节之上，为验证AMSP算法对于网络盗窃案件的分析效果，在XX市刑事案例库中随机抽取网络盗窃案件200例，共涉及嫌疑人56位，为查明侵入、控制计算机信息系统的程序工具、网络盗窃行为的具体作案手段及受害人的网络使用习惯之间的关系，相关业务指标选取如下[10]。

案件基本信息：涉案人员姓名、案发时间；

作案人基本信息：涉案人员姓名、籍贯、受教育程度、是否具有软件编程经验、基本收入状况、是否存在盗窃前科、是否存在盗取个人信息行为、是否曾经买卖个人信息、与受害人是否相识、是否盗窃虚拟财产、是否分工式作案、是否进行非法所得资金转移；

受害人基本信息：涉案人员姓名、性别、职业背景、居住区域、是否为失窃物品报警、是否经常网购、是否经常运行网络游戏、是否存在访问恶意网页现象、是否存在扫描陌生二维码现象；

作案工具基本信息：涉案人员姓名、涉案计算机是否存在木马黑客程序、是否存在网络嗅探工具、计算机中是否存在间歇性打包发送软件、计算机中是否存在Hook抓屏工具、是否曾进行邮件恢复；

根据案件分析的关注点选取上述属性形成的事物数据库，因为网络盗窃常常是同一作案人的多次重复操作，依关注点所导出的事务数据库已经按照涉案人员姓名、案发时间顺序排列，可直接由事务数据库生成序列数据库。在所形成的序列数据库中给定支持度阈值sup(S)=40时，根据AMSP算法，输出频繁概念集上的Hasse图，由于网络盗窃行为数据库中涉及属性较多，其Hasse图局部如图2所示。

根据图2，植入木马程序、盗取个人信息、存在Hook自动抓频工具、盗窃虚拟财产、扫描陌生二维码是最大频繁序列，该种网络盗窃活动往往通过推送二维码种植木马程序于受害人终端设备，再由自动抓屏工具盗取网游空间或交互平台的用户名与密码，实现对虚拟财产的盗窃。仿真分析结果局部如图3所示。

图3 网络盗窃行为序列挖掘结果图

从图2、图3分析可知，网络盗窃犯罪是一针对不特定多数人群实施的短期团伙作案行为，窃取目标不仅仅是以电子数据形式存在的现实财产，还包括虚拟财产。传统盗窃是围绕财物所在物理场所一步实施的非法获取过程，而网络盗窃表现为两步窃取，第一步是窃取个人网络身份认证信息，第二步是利用他人身份认证信息登录账户窃取财物，每一步盗窃所具有的基本特征之间存在时间关联性，第一步是盗窃的基础，其危害性常大于第二步实际财物的盗窃，在2017年6月颁布实施的《中华人民共和国网络安全法》中，将个人信息的基本范围及网络服务商对个人信息的保护责任进行了明确规制，增强个人基本信息的保护可有效遏制网络盗窃犯罪活动的发生。

5 结论

如何有针对性地对短期多发性网络犯罪行为的业务数据进行科学分析，提取网络犯罪活动的整体特征，有效指导防控部署，成为当前网络空间安全领域面临的主要问题之一。网络盗窃活动是典型阶段多发性网络犯罪，具有案发周期短、作案过程时间分布集中等特点，针对网络盗窃活动的数据分析目标与时间序列挖掘的主旨相一致，同时网络盗窃案件的数据记录格式符合时间序列分析的基本条件，因此可将商业领域已成功应用的时间序列挖掘分析算法改进优化并作为网络盗窃犯罪行为的数据分析工具。实例验证表明：量化概念格上的频繁子序列生成算法AMSP可对网络盗窃行为成功拟合，其预测结果将为网络犯罪案件的侦破工作提供新的思维模式。

如何有针对性地对短期多发性网络犯罪行为的业务数据进行科学分析，提取网络犯罪活动的整体特征，有效指导防控部署，成为当前网络空间安全领域面临的主要问题之一。网络盗窃活动是典型阶段多发性网络犯罪，具有案发周期短、作案过程时间分布集中等特点，针对网络盗窃活动的数据分析目标与时间序列挖掘的主旨相一致，同时网络盗窃案件的数据记录格式符合时间序列分析的基本条件，因此可将商业领域已成功应用的时间序列挖掘分析算法改进优化并作为网络盗窃犯罪行为的数据分析工具。实例验证表明：量化概念格上的频繁子序列生成算法AMSP可对网络盗窃行为成功拟合，其预测结果将为网络犯罪案件的侦破工作提供新的思维模式。

[1] 赵秉志.中华人民共和国刑法修正案(九)理解与适用[M].北京:中国法制出版社，2016.

[2] 吕锋,张炜玮.4种序列模式挖掘算法的特性研究[J].武汉理工大学学报.2006,28(2):57-60.

[3] 雷东,王韬,马云飞.基于AC算法的比特流频繁序列挖掘[J].计算机科学.2017,44(1):128-133.

[4] AGRAWAL R, IMIELINSKI T, SWAMI A. Mining association rules between sets of items in large databases[C]∥Proceedings of the ACM SIGMOD Iinternational Conference on Management of Data, 1993:207-216.

[5] GANIER B, WILLE R. Formal concept analysis: mathematical foundations[M]. Berlin: Springer-Verlag,1999:161-180.

[6] WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[C]∥Proceedings of the 7th International Conference on Formal Concept Analysis, 2009: 214-339.

[7] AGRAWAL R, SRIKANT R. Mining sequential patterns[C]∥Proceedings of the 11th International Conference on Data Engineering, 1995: 3-14.

[8] 毛国君,段丽娟,王实，等.数据挖掘原理与算法[M].北京:清华大学出版社，2007.

[9] 王慧,王京.FP-tree上频繁概念格的无冗余关联规则提取[J].计算机工程与应用，2012， 48(15):12-15.

[10] 王慧,郭红涛.基于约简决策表的网络犯罪行为关联分析[J].中国人民公安大学学报，2015(2):67-70.

(责任编辑 陈小明)

公安理论及软科学研究计划项目(2016LLYJGADX003)“面向公安大数据的融合智能网络建设研究”。

王 慧(1973—)，女，内蒙古人，博士，副教授。研究方向为网络信息技术。

D917.7