通话网络的分析度量方法

尹德春, 顾益军, 张 民

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

通话网络的分析度量方法

尹德春, 顾益军, 张 民

(中国人民公安大学信息技术与网络安全学院， 北京 100038)

论述了3种通话网络分析方法：数据统计分析法、可视化关系图分析等、基于PageRank算法的精确度量法。首先简要介绍最常见的数据统计分析法，并在一个简单的测试数据集上，给出了应用实例。该方法的优点是有利于对数据做精确统计计算，但缺点是不便于分析数据之间的关联关系，并且分析结果展现形式也不直观。然后采用可视化关系图分析软件来分析实例中的数据，以弥补数据统计分析法的不足，能够得到更加直观的定性观测分析结果。最后提出采用PageRank算法对可视化关系图做精确定量计算，得到各个节点的权值，从而判断出节点的重要性。这对于解决可视化关系图结果过于复杂、不利于人工观察分析的问题很有效。

通话网络; 数据统计分析; 可视化关系图分析; PageRank

0 引言

通话网络分析在公安业务中起着重要作用。在有组织犯罪案件的侦查过程中，首先需要解决的问题就是还原和分析涉案人员的人际网络[1]，其中最基础的工作之一就是分析相关人员的通话网络。

最常见的通话网络分析方法是数据统计分析法。该方法的优点是有利于对数据做精确统计计算，但缺点是对于节点关联关系的分析过程比较复杂，并且分析结果展现形式不直观。而采用可视化关系图分析软件的方法正好可以弥补这一缺点，能够得到更加直观的定性观测结果。但是，有的时候可视化关系图结果过于复杂，不利于人工观察，或者有时需要对可视化关系图做节点重要性的精确定量计算。因此，本文引入并结合PageRank算法来解决这些问题，从全局角度完成节点重要性的分析计算。下面围绕这3种方法展开详细论述。

1 数据统计分析法

数据统计分析[2]是公安信息化应用中经常采用的方法，是指对相关数据进行整理、分类、计算、分析，进而得到统计结果的过程。如可以统计分析某辖区内某月刑事案件的发案数量、数量的同比和环比变化、不同类型案件的变化、发案地点和时间段的分布等等。这些分析结果以表格或图表的形式来展示。常用的图表形式有曲线图、柱状图、饼图等。这些图形化的结果展示便于观察和分析。

通常，可以借助Excel或Access等办公软件完成这些工作。对于一般性的简单统计分析需求，这些工具足够胜任。但是，对于一些特定的复杂情况，如统计各节点的相关性并绘制节点间的关联关系图，这些常用的统计分析软件使用起来就不太方便，操作难度也很大。如下面的分析需求：在通话话单中找出5个特定号码之间的通话记录，并绘制出对应的关联关系图。假设已经把5个人的通话数据抽取出来，合并后保存在Access的话单数据表T中(实验数据共有1 417条记录)，T的结构定义如图1。

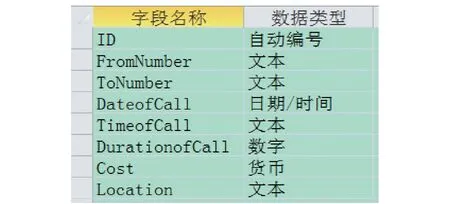
图1 话单数据表的结构定义

可以写出如下SQL语句来完成这个任务：

SELECT FromNumber, ToNumber FROM T

WHERE ToNumber IN

(SELECT DISTINCT FromNumber FROM T);

该SQL查询的运行结果如图2所示，5个号码之间的通话次数总计为43次。

图2 SQL查询的结果

因为Access或Excel无法把这种关联关系分析绘制成可视化的结果图，所以只能人工观察分析这些号码之间的通话关系及其频次。但是，当数据量大的时候，这样做就显然不合适了。因此这类分析需求更适合采用可视化关系图的分析软件来完成。

2 可视化关系图分析法

可视化的关系图分析软件[2]有很多种，如I2、Pajek[3]、Gephi[4]等。图3是把表T中数据导入到可视化分析软件之后得到的节点关系图。可以看出，当节点数较少的时候，要人工观察不同节点之间是否有关联关系以及计算其关联频度，相对还比较容易。但是当节点数量巨大的时候，这个任务就会变得困难。所以需要设定一些过滤和筛选条件，对初始关系图进行剪枝。图4是经过筛选过滤处理之后得到的我们需要的结果，其中只保留了5个节点之间发生的关联关系。节点连线上的数字表示这两个节点之间的通话频次。

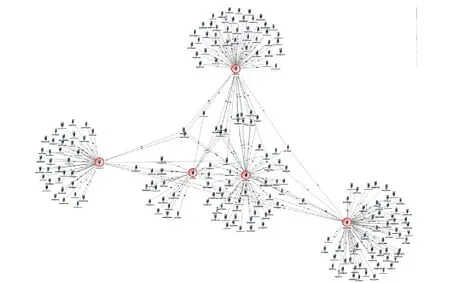
图3 导入初始数据后的可视化关系图

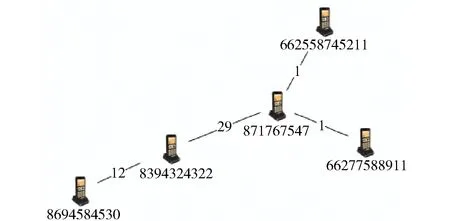
图4 筛选过滤后的5个节点之间的关系图

可以看到，对于数据之间的关联分析问题，采用可视化关系图分析软件是比较好的选择。传统的基于常用办公软件的统计分析及其图表展示方法，不善于完成这样的任务。

关系图分析软件的处理结果可以让我们从直观上观察和推断出一些大致结论，那么如何证明并做精确计量呢？或者当节点数特别多观测不容易、或过滤条件不容易设置的时候，除了用过滤筛选的方法，能否用其他方法计算出节点的关联关系及其权重指标呢？为此，本文尝试引入在搜索引擎领域得到成功应用的PageRank算法[5]，来解决上述问题。

3 基于PageRank算法的通话关系定量分析法

PageRank算法是搜索引擎对搜索结果进行排序的理论依据，它能够计算出互联网上网页节点的重要性并据此给出排序结果。其核心思想是：如果一个网页被很多其他网页所链接，那么说明它受到普遍的“承认”和“信赖”。即它的链入链接越多，它就越权威、越重要(PageRank值越高)。网页权重高的网站贡献的链接权重也大。网页的重要程度(PageRank值)由指向它的其他网页的PageRank值之和决定。

PageRank算法将整个互联网的全部WEB页面看做一个整体，即一个有向图，每一个网页是有向图的一个节点，网页之间的链接关系看作节点之间的有向边。通过定义一个WEB随机矩阵(Stochastic Matrix of the Web)来描述网络中下一步访问的行为。假设该随机矩阵M中的元素mij表示处在网页j的访问者下一步访问网页i的概率。如果网页j中一共有n个链接，其中一个链向网页i，那么有mij=1/n；如果网页j中不包含链向网页i的链接，则mij=0。如果网页数目为n，则该矩阵M就是一个n行n列的方阵。M其实就是网页跳转概率矩阵。

下面为描述方便，把图4中号码用字母代替，如图5所示。

图5 可视化关系图的简化表示

这里，我们把通话网络分析问题转化为WEB网络分析。由于通话网络与WEB网络不同，所以需要做一些变换处理。仍以图4的简单通话网络为例，把图4中的各个节点视作网页，通话关系视作双向的网页链接关系，也就是节点之间的互相访问关系。然后，定义一个WEB随机矩阵M。假设M中的元素mij表示节点j访问节点i的概率。如果节点j一共有n次通话记录，其中与节点i的通话次数是ni次，那么有mij=ni/n；如果节点j没有与节点i通话，他们之间没有链接关系，则mij=0。此例中，节点数目为5，则矩阵M就是一个维度为5的方阵。由图4构造出的矩阵M如下。

矩阵M的第一列表示节点A分别以0、1、0、0、0的概率访问节点A、B、C、D、E；第二列表示节点B分别以12/41、0、29/41、0、0的概率访问节点A、B、C、D、E；以此类推。

定义n维向量V=[p1,p2,…,pj,…,pn]T为访问者位置的概率分布，满足p1+p2+…+pj+…+pn=1。pj表示访问者处于节点j的概率。如果访问者由节点j进入节点i，其概率为pi=mij*pj。V其实就是位置概率矩阵。假设初始的概率分布状态为V0，随机矩阵为M，则第一步转移之后访问者的概率分布向量为V1=MV0，第二步转移之后的概率分布向量为V2=MV1=M(MV0)，以此类推，经过i次左乘M，访问者经过i步转移之后的位置概率分布向量为Vi=MVi-1。

PageRank模型将网页浏览作为一个随机过程，将一个网页浏览者的随机浏览WEB的行为作为马尔可夫链中的一个状态转移。每张网页或者网络图中的每个节点都被认为是一个状态，一个超链接就是从一个状态到另一个状态的带有一定概率的转移。根据马尔可夫链的各态历经定理，可知随机矩阵M定义的有限马尔可夫链具有唯一的静态概率分布。这意味着经过一系列的状态转移之后，不管所选择的初始状态V0是什么，V都会收敛到一个稳定的状态概率向量V=M*V，它表示的是长时间后访问者最可能处于的位置，也就是我们要求的各个节点的PageRank值。

迭代计算PageRank值的方法如下：首先根据节点间的链接关系，构建随机矩阵M，定义初始概率分布向量V0=[p1,p2,…,pj,…,pn]T，满足p1+p2+…+pj+…+pn=1。比如可以初始化为V0=[1/n,1/n,…,1/n]T，此时各节点具有同等的概率或重要性；或者随机分配总和为1的n个实数也可以。然后，用M不断左乘V，让概率(重要性)在节点间随机游走，直到前后两轮迭代产生的结果向量相差很小(小于给定的阈值)的时候停止。

如对图4对应的矩阵M进行上述迭代运算。初始向量设置为V0=[1/5,1/5,1/5,1/5,1/5]T，通过不断左乘随机矩阵M，得到以下结果(论文中小数点后只保留3位，做了四舍五入处理)：

当迭代次数i=20，V收敛到[0.112, 0.572, 0.288, 0.014, 0.014]T。也就是说，此后无论继续左乘M多少次，V都不再变化。V的每一行取值分别是节点A、B、C、D、E的PageRank值。其中，节点B的PageRank值最大，节点C次大，节点D和E最小。

由于真实的WEB结构中PageRank计算存在“终止点”和“采集器陷阱”问题[2]，所以经常采用改进后的PageRank算法“抽税法”进行计算。在该方法中，给每一个页面增加指向所有页面的链接，每个链接都赋予一个由参数β控制的转移概率。这种改进的PageRank模型中，在任何一个网页上，一个随机访问者将有两种选择：(1)随机点击一个链出链接继续浏览，此时的概率为β(β取值通常在0.8到0.9之间)；(2)不点击链接，而是直接打开另一个随机网页，此时的概率是1-β，也就是这里所说的“税”。改进的PageRank模型为：

V′=βMV+(1-β)e/n

其中，n是WEB图中所有节点的数目；e是一个n维单位向量，它的所有分量都为1。

这样即使WEB结构中存在终止点，由于(1-β)e/n的存在，V的分量之和永远不会为0。WEB访问者总会离开终止点，以一定概率跳转至非终止点。

下面采用“抽税法”来重新计算图4中各节点的PageRank值。取β=0.85，初始向量为V0=[1/5,1/5,1/5,1/5,1/5]T，迭代过程中向量V′和V差值的阈值设置为0.000 000 000 1。在经过134次迭代后，V′和V的差值小于设定阈值，V收敛。迭代计算过程中V的取值变化如下(论文中小数点后只保留3位，做了四舍五入处理)：

迭代134次后V收敛到[0.137, 0.429, 0.355, 0.040, 0.040]T。V的每一行取值分别是节点A、B、C、D、E的PageRank值。其中，节点B的PageRank值最大，节点C次大，节点D和E最小。

可以看到，无论是采用原始PageRank算法还是改进后的“抽税法”计算，5个节点PageRank值的大小顺序都是不变的，重要性排序依次为B>C>A>D=E。

以上是使用PageRank及其改进算法分析简单通话数据的过程。通常，在通话网络分析中，要面对和解决的更一般问题是：在大数据量环境下，节点数非常多的时候，要求分析所有通话数据，判断出各个节点的重要等级，找出相对重要的节点。对于此类问题可以直接用PageRank算法或其改进后的“抽税法”计算全部节点的重要性指标值，然后由大到小排序输出即可。

4 结论

本文初步总结和探讨了通话网络的分析度量方法，并重点研究了如何将原本用于WEB网页搜索排序的PageRank算法应用于通话网络中节点重要性的计算，给出了推理和计算过程，得到的实验结果验证了该方法的正确性和有效性。

需要指出的是，上述3种方法并没有绝对的优劣之分，各自都有适用场合和优缺点。在业务实践中，单独只采用某一种分析方法往往是不够的，需要综合应用才能得到准确全面的分析结果。

[1] 顾益军,解易,张培晶. 面向有组织犯罪分析的人际关系网络节点重要性评价研究[J].中国人民公安大学学报(自然科学版)，2013(4):66-68.

[2] 顾益军. 网络情报获取与分析[M].北京:中国人民公安大学出版社,2014.

[3] 沃特·德·诺伊，等. 蜘蛛：社会网络分析技术[M].林枫，译. 北京:世界图书出版公司,2012.

[4] 刘勇,杜一.网络数据可视化与分析利器：Gephi 中文教程[M].北京:电子工业出版社,2017.

[5] BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[C]∥International Conference on World Wide Web, 1998: 107-117.

(责任编辑 陈小明)

公安部技术研究计划项目(2014jsya023)“基于云计算的微警务信息支撑平台关键技术研究”。

尹德春(1979—)，男，吉林人，博士，讲师。研究方向为自然语言处理、情报分析。

D035.39