时间误差分析的双基地运动目标聚焦成像方法*

夏猛

(西安科技大学 通信与信息工程学院，陕西 西安 710054)

时间误差分析的双基地运动目标聚焦成像方法*

夏猛

(西安科技大学 通信与信息工程学院，陕西 西安 710054)

在推导目标回波相位历程的基础上，分析了双基地系统中的收、发时间误差对距离向和方位向处理造成的影响，并构造了相应的补偿因子，同时给出了基于相位中心偏置天线的星机双基地杂波对消约束条件。针对运动目标的距离徙动使用二阶Keystone变换和Radon变换对其进行校正，为了构造精确的方位压缩匹配滤波器利用修正离散调频傅里叶变换进行多普勒参数估计。最后计算机仿真验证了所提方法的有效性。

合成孔径雷达；双基地；时间误差；运动目标；聚焦成像；参数估计

0 引言

由于不受地理、天气、观测时间等条件的限制，利用星载或机载合成孔径雷达(synthetic aperture radar，SAR)进行地面运动目标检测(ground moving target indication，GMTI)受到越来越多的关注并且发展出了各种处理算法，使其广泛运用于军事侦查和民用测绘领域[1-6]。单一的星载或机载SAR-GMTI系统即要发射信号同时也对回波进行处理，随着电子侦查和反辐射技术的发展，收发一体模式的系统受到的威胁越来越大。为了提高系统的战场生存能力，出现了星地双基(卫星发射信号地面站接收回波并处理)、星机双基(卫星发射信号飞机接收回波并处理)等多种形式的双基地SAR-GMTI。

文献[7]提出了星地双基SAR-GMTI并分析了通道失配和约束条件失配对杂波抑制的影响，但该模式下低轨道卫星的重访周期限制了系统的连续观测性能。文献[8]提出了星机双基模式的SAR-GMTI并在分数阶傅里叶变换(fractional fourier transform，FrFT)的基础上完成目标的聚焦成像和参数估计。文献[9]分析了基于二次距离压缩的“Tandem”模式双基地SAR系统，并给出了基于距离徙动校正和偏移补偿的聚焦算法。文献[10]分析了双基前视SAR成像体制在弹载平台上的频率误差和同步误差模型。

本文提出同步轨道卫星结合机载双通道SAR的双基地SAR-GMTI系统，实现了对场景的连续观测而不受卫星重访周期的限制。在推导目标回波相位历程的基础上重点分析了双基地系统中的收、发时间误差对距离向和方位向处理造成的影响，并给出了相应的补偿因子，同时推导了基于相位中心偏置天线(displaced phase center antenna，DPCA)技术杂波抑制的星机双基地约束条件，在利用二阶Keystone变换和Radon变换对目标距离徙动进行校正的同时实现时间误差的补偿处理，为了实现对运动目标的聚焦成像这里使用修正DCFT(modified discrete chirp-fourier transform，MDCFT)完成多普勒参数估计并构造方位向匹配滤波器。

1 星机双基地时间误差分析和约束条件

同步轨道卫星结合机载双通道SAR的星机双基地运动目标检测系统如图1所示，假设卫星S位于地球同步轨道，轨道高度为H，载机以速度va沿航迹向匀速运动且放置间隔为d的两幅接收天线s1和s2。慢时间tm=0时，地心赤道坐标系中同步轨道卫星坐标为(Xs，Ys，H)，载机上两接收天线坐标分别为(0，0，h)和(d，0，h)，其中h为载机飞行高度，为方便分析假设一段时间内飞行高度保持不变。同时，场景中运动目标初始坐标为(x0，y0，0)并且以速度(vx，vy，0)做匀速运动。卫星发射线性调频信号，载机上的两副天线同时接收目标回波，构成收发分置的星机双基地SAR-GMTI系统。

图1 星机双基地SAR-GMTI系统Fig.1 Spaceborne-airborne bistatic SAR-GMTI

下面分析星机双基地SAR-GMTI系统中由于收、发分置特性造成的收、发时间误差对运动目标聚焦成像的影响以及基于DPCA杂波对消的约束条件。首先卫星与目标瞬时斜距RT(tm)经过泰勒展开后为[11]

(1)

其次接收天线与目标的瞬时斜距Ri(tm)，i=1，2，经过泰勒展开后为

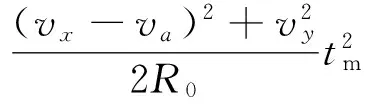
(2)

(3)

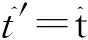
(4)

分析收、发时间误差对距离向和方位向处理造成的影响。其中距离向会造成测距误差，影响回波包络校正，后面会具体分析；方位向上造成位置偏移和分辨力下降，这里假设系统采样窗的宽度设计满足对存在时间误差信号的完全采样。实际中可以对回波数据进行拟合估计得到时间误差量，然后利用时间误差量构造补偿因子对接收机混频后的回波数据进行误差补偿处理，补偿因子取为exp(j2πfcτ)，以消除对方位向的影响。

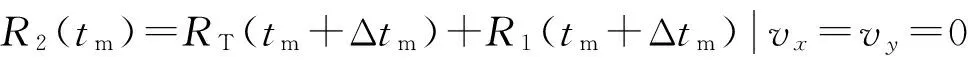
(5)

由于d≤R0和vaΔtm≤R0，由式(5)可以得到

(6)

式(6)即为基于DPCA的星机双基地SAR-GMTI杂波对消约束条件，在满足该条件时两通道的静止目标在时间补偿后可以完全消除。以下分析均假设系统满足该条件。

2 基于时间误差分析的回波距离徙动正

如果场景中存在快速运动目标或是积累时间较长，运动目标回波在完成距离压缩后将会出现距离徙动现象，此时回波能量不再沿方位向直线分布，而是表现为倾斜的曲线，即回波会跨越多个距离单元并且呈现出一定的弯曲。其中，距离向和方位向的一次耦合称为距离走动，距离向和方位向的二次耦合称为距离弯曲，如果不对其进行校正处理会影响到方位向能量聚焦。本文在此利用对距离向压缩及杂波对消后的运动目标使用二阶Keystone变换[12]进行距离弯曲校正，在距离频域补偿剩余距离走动的方法进行回波校正，并分析收、发时间误差对回波包络的影响，同时给出相应的误差补偿因子，最后在精确估计方位向多普勒参数的基础上完成运动目标的聚焦成像。

载机上2幅天线接收的目标回波在完成方位向时间补偿和距离向压缩后可写为

(7)

式中：A为距离压缩后的信号幅度；i=1，2；Δf表示发射线性调频信号的带宽；aa(·)为方位矩形窗函数。

星机双基地SAR-GMTI系统在满足式(6)的约束条件下，将2幅天线回波数据经过时间补偿并进行DPCA对消后的结果变换到距离频域、方位时域得到：

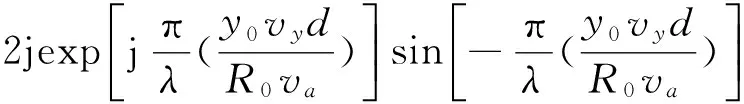
(8)

式中：A′为信号幅度；fr为距离频率；ar(·)距离矩形窗函数。

分析式(8)，第1个指数项包含方位频域和距离时间的耦合相位，同时还包含收、发时间误差τ的影响，需要重点加以分析；第2个指数项为杂波对消后运动目标速度引起的相位，不影响聚焦成像处理；最后一项影响系统的盲速点分布。

将式(2)代入式(8)中的耦合相位得到

(9)

(10)

将式(10)代入式(8)忽略常数相位并完成剩余距离走动校正后进行距离向傅里叶逆变换得到

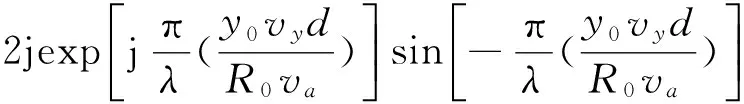
(11)

式(10)即为杂波抑制后，运动目标回波距离徙动得到校正的结果。此时，可以看出收、发时间误差τ明显影响回波的包络位置，造成的距离误差为cτ/2。因此，在利用Keystone变换进行包络校正时，需要进行二次误差补偿，即构造补偿因子exp(j2πfrτ)在距离频域、方位时域与式(8)相乘。经过上述校正处理后目标信号聚集在某个距离单元上而与慢时间无关，下来再进行方位向聚焦处理。

3 运动目标聚焦成像与参数估计

运动目标回波完成距离徙动校正后如果仍使用静止目标的参数进行方位向压缩将会出现散焦现象，因此聚焦成像的关键是构造精确的方位向压缩匹配滤波器。在此，使用修正DCFT结合最小波形熵搜索的方法进行多普勒参数估计。

(12)

(13)

完成多普勒中心补偿后，构造方位向聚焦处理的多普勒域滤波器为

(14)

利用式(14)即可实现运动目标的方位向聚焦成像，得到成像结果为

(15)

式中：L为合成孔径长度，运动目标方位向成像结果与匹配滤波器直接相关，或者说方位向多普勒调频率决定聚焦效果，为此必须对调频率进行精确估计。为了获得精确的运动目标成像结果，这里采用修正DCFT方法对杂波抑制后数据进行方位向多普勒参数估计。

文献[13]给出了基于MDCFT处理的具体参数估计方法。同时为了能够对回波中的多目标进行处理，采用基于CLEAN思想[14]并结合最小波形熵的快速搜索算法，能够实现对参数的精确估计[15]。波形熵是用于衡量一个信号波形的能量沿其参数轴发散程度的概念，当能量越集中时对应波形熵就越小。同时，在搜索过程中由于分为粗、精两次计算回波信号的MDCFT，相应计算量也会大幅减小。在得到调频率的精确估计值后由式(14)构造方位向压缩匹配滤波器实现运动目标的聚焦成像。

4 仿真校验

地心赤道坐标系中存在一个静止目标和3个运动目标，雷达工作波长λ=0.03 m，脉冲重频周期1 000 Hz，信号带宽100 MHz，载机运动速度200 m/s，飞行高度h=10 000 m，静止轨道卫星坐标设为(1，0，36 000)km，且卫星和载机之间存在200 ns的收、发时间误差，系统工作在正侧视模式下。图2a)所示为通道1距离压缩后的结果，包含3个运动目标和一个静止目标，且由于存在收、发时间误差使得距离压缩后目标存在测距误差，误差量为295.8 m；如图2b)所示为经过收、发时间误差补偿因子补偿后的结果，经过补偿后目标回到真实的距离单元，但同时相应运动目标距离徙动非常明显。此时，静止目标虽然被完全抑制掉，但是由于运动目标具有较大的速度矢量出现距离徙动现象，即距离压缩后运动目标回波跨越多个距离单元且带有一定的弯曲量。采用文中所述二阶Keystone变换校正距离弯曲，Radon变换求得距离走动量进行距离走动校正后某一运动目标处理后结果如图2c)所示。校正后目标回波沿方位向直线分布，然后再进行方位向参数估计和聚焦成像处理。

图2 时间误差补偿和回波距离徙动校正Fig.2 Time error compensation and range migration correction

图3 目标回波的MDCFT与成像结果Fig.3 MDCFT and imaging results of target echo

5 结束语

同步轨道卫星结合机载双通道SAR的双基地运动目标成像系统能够实现对场景的连续观测，而不受天气、时间等外部因素的影响。本文在推导回波模型的基础上，分析了收、发时间误差对系统聚焦成像的影响，针对运动目标的距离徙动和收、发时间误差的影响，利用二阶Keystone变换和Radon变换加以校正。本文分析研究结果对星机双基地系统设计具有一定的理论和工程实际意义。

[1] 左伟华，皮亦鸣，闵锐.大斜视机载聚束SAR时域校正距离走动的频率尺度成像算法[J].电子学报，2013，41(9)：1716-1723. ZUO Wei-hua，PI Yi-ming，MIN Rui.Improved Frequency Scaling Algorithm Based on the Range Walk Correction in Time Domain For High Squint Spotlight Airborne SAR[J].Acta Electronica Sinica，2013，41(9)：1716-1723.

[2] WONG F H，CUMMING I G，NEO Y L.Focusing Bistatic SAR Data Using the Nonlinear Chirp Scaling Algorithm[J].IEEE Trans on Geoscience and Remote Sensing，2008，46(9)：2493-2505.

[3] AN Dao-xiang，HUANG Xiao-tao，JIN Tian，et al.Extended Two-Step Focusing Approach for Squinted Spotlight SAR Imaging[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50(7)：2889-2900.

[4] 孙娜，周荫清，李景文.基于DPCA 技术的星载SAR/GMTI处理方法[J].电子与信息学报，2005，27(10)：1564-1568. SUN Na，ZHOU Yin-qing，LI Jing-wen.Algorithm of Spaceborne SAR/GMTI Based on DPCA[J].Journal of Electronics and Information Technology，2005，27(10)：1564-1568.

[5] SUN Hua-dong，SU Fu-lin，GAO Jian-jun，et al.Parameter Estimations of SAR Moving Target Based on DPCA-FrFT Algorithm[C]∥IEEE Conference on Industrial Electronics and Applications，2007：1779-1784.

[6] 张升，孙光才，李学仕，等.一种新的基于瞬时干涉的SAR-GMTI精聚焦和定位方法[J].电子与信息学报，2015，37(7)：1729-1735. ZHANG Sheng，SUN Guang-cai，LI Xue-shi，et al.Multi-Channel Synthetic Aperture Radar-Ground Moving Target Indication High-Accuracy Focusing and Positioning Using Instantaneous Interferometry[J].Journal of Electronics and Information Technology，2015，37(7)：1729-1735.

[7] 陈娟，王盛利.基于二天线的双基地DPCA技术[J].电子与信息学报，2007，29(7)：1687-1690. CHEN Juan，WANG Sheng-li.Bistatic Radar DPCA Technique Based on Two-Anntena[J].Journal of Electronics and Information Technology，2007，29(7)：1687-1690.

[8] 史洪印，周荫清，陈杰.同步轨道星机双基地三通道SAR地面运动目标指示算法[J].电子与信息学报，2009，31(8)：1881-1885. SHI Hong-yin，ZHOU Yin-qing，CHEN Jie.An Algorithm of GEO Spaceborne-Airborne Bistatic Three-Channel SAR Ground Moving Target Indication[J].Journal of Electronics and Information Technology，2009，31(8)：1881-1885.

[9] 张升康，杨汝良.基于二次距离压缩的双基地合成孔径雷达斜视成像算法[J].电子与信息学报，2008，30(7)：1717-1721. ZHANG Sheng-kang，YANG Ru-liang.A Squint Mode Bistatic Synthetic Aperture Radar Image Formation Algorithm Based on Second Range Compression[J].Journal Of Electronics and Information Technology，2008，30(7)：1717-1721.

[10] 孟自强，李亚超，胡奇，等.弹载双基前视SAR建模及运动/同步误差分析[J].系统工程与电子技术，2015，37(3)：523-531. MENG Zi-qiang，LI Ya-chao，HU Qi，et al.Modeling and Motion/Synchronization Error Analysis of MBFL-SAR[J].Systems Engineering and Electronic，2015，37(3)：523-531.

[11] 吕孝雷，齐飞林，邢孟道，等.三通道SAR-GMTI地面快速目标检测[J].系统工程与电子技术，2009，31(7)：1581-1587. LÜ Xiao-lei，QI Fei-lin，XING Meng-dao，et al.Ground Fast Moving Target Detection Based on Tri-Channel SAR-GMTI[J].Systems Engineering and Electronic，2009，31(7)：1581-1587.

[12] 周峰，李亚超，邢孟道，等.一种单通道SAR地面运动目标成像和运动参数估计方法[J].电子学报，2007，35(3)：543-548. ZHOU Feng，LI Ya-chao，XING Meng-dao，et al.An Effective Approach to Ground Moving Target Imaging and Motion Parameter Estimation for Single Channel SAR System[J].Acta Electronica Sinica，2007，35(3)：543-548.

[13] 孙泓波，郭欣，顾红，等.修正离散Chirp-Fourier变换及其在SAR运动目标检测中的应用[J].电子学报，2003，31(1)：1-4. SUN Hong-bo，GUO Xin，GU Hong，et al.Modified Discrete Chirp-Fourier Transform and Its Application to SAR Moving Target Detection[J].Acta Electronica Sinica，2003，31(1)：1-4.

[14] CHOI I S，KIM H T.Two-Dimensional Evolutionary Programming-Based Clean[J].IEEE Trans.Aerosp.Electron，Syst.，2003，39(1)：373-382.

[15] 夏猛，杨小牛.双星双频地面快速运动目标成像与参数估计[J].宇航学报，2012，33(1)：100-106. XIA Meng，YANG Xiao-niu.Ground Fast Moving Target Imaging and Parameters Estimation with Dual-Satellite/Dual-Frequency[J].Journal of Astronautics，2012，33(1)：100-106.

[16] 夏猛.多通道SAR系统地面运动目标信息获取方法研究[D].西安：西安电子科技大学，2012. XIA Meng.Study on Ground Moving Target Information Acquisition Based on Multi-Channel SAR System[D].Xi’an：Xidian University，2012.

Bistatic Moving Target Focused Imaging Method Based on Time Error Analysis

XIA Meng

( Xi’an University of Science and Technology，Communication and Information Engineering College，Shaanxi Xi’an 710054，China)

Based on the analysis of echo phase, the impact of time error on range and azimuth is analyzed and the corresponding compensation factors are also given. Meanwhile, the DPCA clutter cancellation constraints for spaceborne-airborne bistatic system are derived. General two-order Keystone transform and Radon transform are applied to eliminate range migration. In order to construct azimuth matched filter, the modified discrete chirp-Fourier transform is employed to Doppler parameters estimation. Finally, the computer simulation results validate its effectiveness.

synthetic aperture radar(SAR)；bistatic；time error；moving target；focused imaging；parameter estimation

2016-03-09；

2016-09-30

校博士启动基金(2015QDJ059)；博士培育基金(201666)

夏猛(1981-)，男，陕西安康人。讲师，博士，主要研究方向为SAR运动目标检测和参数估计。

通信地址：710054 西安科技大学通信与信息工程学院(西安市雁塔路58号) E-mail：xia228@163.com

10.3969/j.issn.1009-086x.2017.03.017

TN957.52；TP391.9

A

1009-086X(2017)-03-0104-07