阅读理解题新走向
文/房延华
阅读理解题新走向
文/房延华
责任编辑:王二喜
阅读理解题是指先给出阅读材料,通过阅读领会其中的数学内容、方法要点,并能加以运用的一类题型.阅读理解题的篇幅一般较长,试题结构分两部分:一部分是阅读材料,另一部分是需要解决的有关问题.读懂并理解阅读材料中提供的新情景、新方法、新知识等,并能迅速进行知识的迁移与转化是解阅读理解题的关键.
一、新知识阅读理解题
温馨提示:以没有学过的高中知识为背景设计中考试题,已成为这几年中考命题的新亮点.解决这类问题,要认真阅读,模仿解题.
二、新方法阅读理解题
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
解:(1)如图1所示.
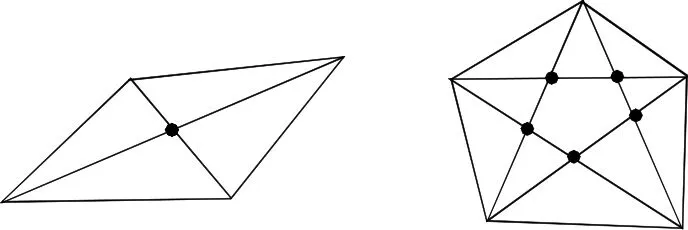
图1
填1;5.
(2)将(1)中的数值代入公式,得
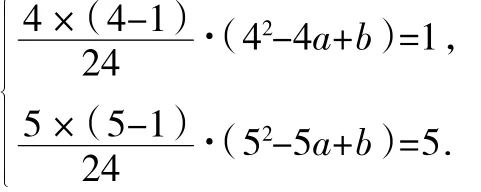
温馨提示:本题属于基础题,难度不大.依据题意画出图形,利用数形结合解决问题.这类题考查我们接收信息、加工信息和利用信息的能力.
三、新概念阅读理解题
例3(2016年重庆卷)我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q)援在n的所有分解中,如果p,q两因数之差的绝对值最小,就称p×q是n的最佳分解,并规定例如12可分解成1×12,2×6或3×4,12-1>6-2>4-3,所以3×4是 12的最佳分解
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数援求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位数与十位数得到新数,新数减去原数的差为18,那么称t为“吉祥数”.求所有“吉祥数”中F(t)的最大值.
解:(1)对任意一个完全平方数m,设m=n(2n为正整数),
∵|n原n|=0,
∴n×n是m的最佳分解,
(2)设交换t的个位数与十位数得到的新数为t′,则t′=10y+x.
∵t为“吉祥数”,
∴t′原t=(10y+x)-(10x+y)=9(y原x)=18,
∴y=x+2.
∵1≤x≤y≤9,x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79.
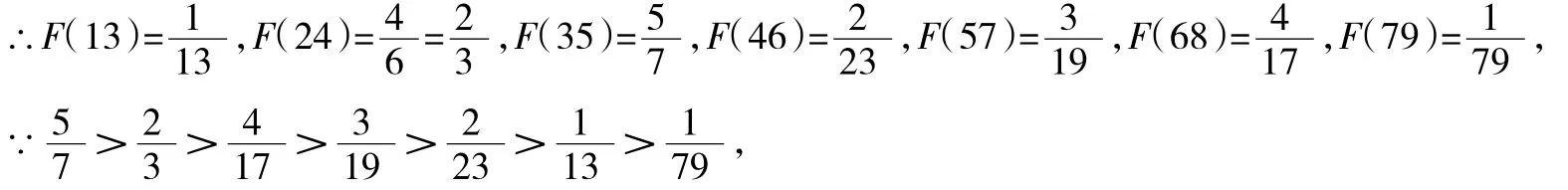
温馨提示:本题主要考查实数的运算.理解最佳分解、“吉祥数”的定义,并将其转化为实数的运算是解题的关键.
四、探究型阅读理解题
解探究型阅读理解题需要对材料进行加工和提炼,需要具备较强的综合运用知识的能力.这类题主要考查应用数学的意识和能力.
例5(2016年烟台卷)【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.
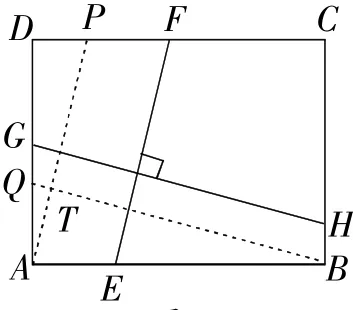
图2
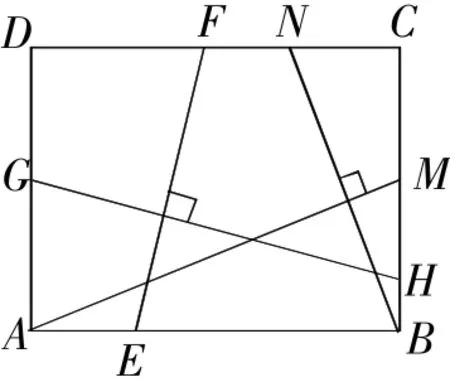
图3
【结论应用】
(2)如图3,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若,则的值为______.
【联系拓展】
(3)如图4,四边形ABCD中,蚁ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上援
∵四边形ABCD是矩形,
∴AB∥DC,AD∥BC援
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ援
又∵GH⊥EF,
∴AP⊥BQ,
∴蚁QAT+蚁AQT=90°.
∵四边形ABCD是矩形,
∴蚁DAB=蚁D=90°,
∴蚁DAP+蚁DPA=90°,
∴蚁AQT=蚁DPA援
∴△PDA~△QAB,
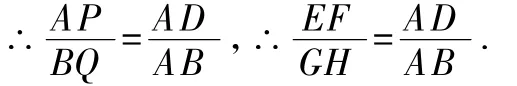
(2)如图3,∵EF⊥GH,AM⊥BN,
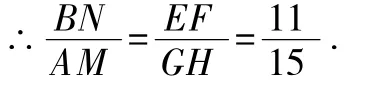
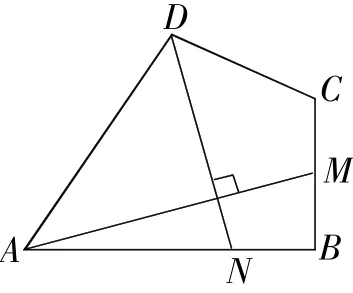
图4
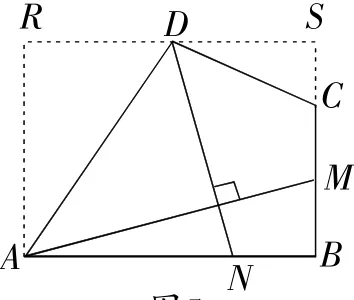
图5
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图5,则四边形ABSR是平行四边形.
∵蚁ABC=90°,
∴▱ABSR是矩形,
∴蚁R=蚁S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
设SC=x,DS=y,则AR=BS=5+x,RD=10原y,

由①③得x=原5,y=0(舍去),或x=3,y=4,
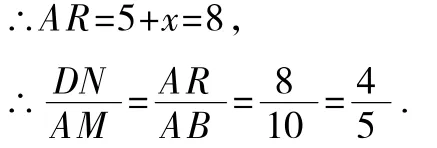
温馨提示:解这类题需要根据题目的探究步骤,合理利用已证明的结论逐问解答.

