方案设计题的分类解答

方案设计题的分类解答

责任编辑：王二喜

解答方案设计型问题需要根据问题所提供的信息，运用学过的技能和方法进行简单的设计与操作，经过分析、计算、证明等，确定最佳方案.方案设计题有以下几种类型.

一、利用方程设计方案

例1（2016年牡丹江卷）某绿色食品有限公司购进A和B两种蔬菜，B种蔬菜每吨的进价比A种蔬菜每吨的进价多0.5万元，经计算用4.5万元购进A种蔬菜的吨数与用6万元购进B种蔬菜的吨数相同.请解答下列问题：

（1）求A，B两种蔬菜每吨的进价；

（2）该公司计划用14万元同时购进A，B两种蔬菜，若A种蔬菜以每吨2万元的价格出售，B种蔬菜以每吨3万元的价格出售，且全部售出.请求出所获利润W（万元）与购买A种蔬菜的资金a（万元）之间的函数关系式；

（3）在（2）的条件下，要求A种蔬菜的吨数不低于B种蔬菜的吨数，若公司欲将（2）中的最大利润全部用于购买甲、乙两种型号的电脑赠给某中学，甲种电脑每台2100元，乙种电脑每台2700元.请直接写出有几种购买电脑的方案．

解：（1）设A种蔬菜每吨的进价为x万元，则B种蔬菜每吨的进价为（x+0.5）万元.

解得x=1.5，

经检验，x=1.5是原方程的解，

∴x+0.5=2，

∴A种蔬菜每吨的进价为1.5万元，B种蔬菜每吨的进价为2万元.

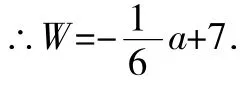
∴当a=6时，W有最大值，最大值为-1+7=6（万元）.

设购买甲种电脑c台，乙种电脑b台，则2100c+2700b=60 000，

∵c和b均为正整数，

∴c=26，b=2；c=17，b=9；c=8，b=16.

有三种购买方案．

点评：利用方程设计方案需要建立方程，确定方程的解，进而由整数的意义并结合题意，确定方案.

二、利用不等式设计方案

例2（2016年恩施卷）在清江河污水网管改造建设中，需要确保在汛期来临前将建设过程中产生的渣土清运完毕，每天至少需要清运渣土12 720m3.施工方准备每天租用大、小两种运输车共80辆，已知每辆大车每天运送渣土200m3，每辆小车每天运送渣土120m3，大车、小车每天每辆租车费用分别为1200元、900元，且要求每天租车的总费用不超过85 300元.请解答下列问题：

（1）施工方共有多少种租车方案？

（2）哪种租车方案费用最低，最低费用是多少？

解：（1）设施工方租用大车x辆，小车(80-x)辆.

∵x为整数，

∴x=39，40，41，42，43，44.

施工方共有6种租车方案：①大车39辆，小车41辆；②大车40辆，小车40辆；③大车41辆，小车39辆；④大车42辆，小车38辆；⑤大车43辆，小车37辆；⑥大车44辆，小车36辆.

（2）设租车费用为y.由已知得，

y=1200x+900（80-x）=72000+300x，

∴当x最小时,y最小,即方案①租大车39辆，小车41辆的费用最低.

最低费用为39×1200+41×900＝83 700（元）.

点评：解不等式的方案设计问题，一般可转化为求不等式组的整数解，有时需要从表格中获取相关信息.要认真审题，理解各数量之间的关系.

三、利用函数设计方案

例3（2016年盐城卷）某地拟召开一场安全级别较高的会议，预估将有4000至7000人参加会议.为了确保会议的安全，会议组委会决定对每位入场人员进行安全检查．现有门式安检仪和手持安检仪两种：门式安检仪每台3000元，需安检员2名，每分钟可通过10人；手持安检仪每台500元，需安检员1名，每分钟可通过2人.该会议中心共有6个不同的入口，每个入口都有5条通道可供使用，每条通道只可安放一台门式安检仪或一台手持安检仪.每位安检员的劳务费用均为200元.（安检总费用包括安检设备费用和安检员的劳务费用.）

与会人员从上午9∶00开始入场，到上午9∶30结束入场，6个入口都采用相同的安检方案，所有人员须提前到达并根据会议通知从相应入口进入.

（1）如果每个入口处，只有2个通道安放门式安检仪，而其余3个通道均为手持安检仪.在这个安检方案下，请问：在规定时间内可通过多少名人员？安检总费用为多少元？

（2）请你设计一个安检方案，确保安检工作的正常进行，同时使得安检总费用尽可能少.

解：（1）可通过人数：（2×10+3×2）×30×6=4680（人）．

一个入口的安检费用：2×3000+3×500+（2×2+3）×200=8900（元），

总安检费用：8900×6=53400（元）.

（2）设每个入口处安放x台门式安检仪，（5-x）台手持安检仪，通过的总人数为y，总安检费用为w，则有

y＝[x×10+（5-x）×2]×30×6=1440x+1800，

由于可能有4000至7000人参加会议，

又∵x≤5，∴x=4或5.

w=[x×3000+（5原x）×500+（2x+5原x）×200]×6＝16 200x+21 000，x越小，w越小，

∴当x=4时，即每个入口处安放4台门式安检仪，1台手持安检仪，安检总费用较少.

另外，每个入口处安放4台门式安检仪，剩余1个通道封闭，可通过的总人数为4×10× 30×6=7200，∵7200＞7000，且费用更少，也满足方案设计的需要.

综上所述，安检方案为：每个入口处安放4台门式安检仪，剩余的1个通道关闭.

评点：根据背景材料或图表信息，确定相应的函数关系，由函数的性质并结合自变量的取值范围求解.

四、利用图形设计方案

例4（2015年义乌卷）某校规划在一块长AD为18m，宽AB为13m的长方形ABCD场地上，设计分别与AD，AB平行的横向通道和纵向通道，其余部分铺上草皮．

（1）如图1，若设计三条通道，一条横向，两条纵向，且它们的宽度相等，其余六块草坪相同，其中一块草坪两边之比AM∶AN=8∶9.问通道的宽是多少？

（2）为了建造花坛，要修改（1）中的方案，如图2，将三条通道改为两条通道，纵向的宽度改为横向宽度的2倍，其余四块草坪相同，且每一块草坪均有一边长为8m.在草坪上建造花坛，如图3，在草坪RPCQ中，已知RE⊥PQ于点E，CF⊥PQ于点F援求花坛RECF的面积．

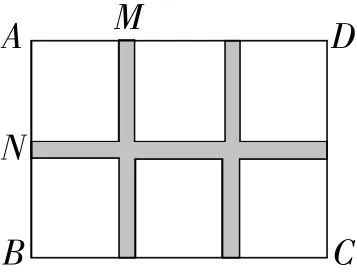
图1

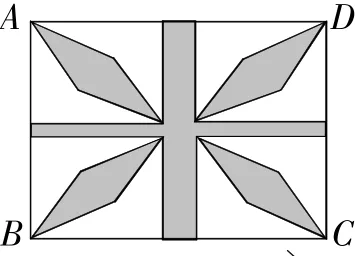
图2

图3

解：（1）设通道的宽为xm，AM=8ym.

答：通道的宽是1m.

（2）四块相同草坪中的每一块，有一条边长为8m，

若RP=8，则AB＞13，不合题意，

∴RQ=8.

∴纵向通道的宽为2m，横向通道的宽为1m，

∴RP=6.

∵RE⊥PQ，四边形RPCQ是长方形，

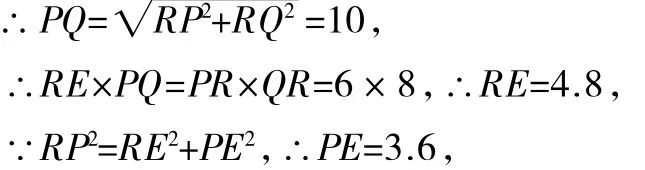
同理可得QF=3.6，

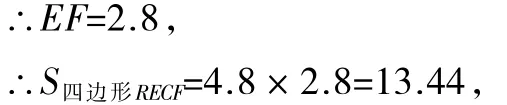
即花坛RECF的面积为13.44m2.

点评：求出RP的长是解题关键.