杜绝“拿来主义”，改编推进发展

☉江苏东台市实验中学教育集团南校区 崔恒刘

杜绝“拿来主义”，改编推进发展

☉江苏东台市实验中学教育集团南校区 崔恒刘

一、话题起因

备课是每个老师必做的课前准备工作，布置给学生练习的题，习惯上也喜欢自己先计时做一遍，学生考试时只要有可能必与学生同考，我的感觉是只有自己亲自做了，才能知晓试题，明确教学目标，讲解时才会有针对性，打造高效的课堂.最近在做我市《2017中考说明与训练》的综合训练三时，对于填空压轴题，做后感悟颇多，在此与大家交流，原题是：

如图1，在平面直角坐标系中，直线l平行于x轴，交y轴于点A，第一象限内的点B在l上，连接OB，动点P在直线OB上运动且满足∠APQ=90°，PQ交x轴于点C.点D是直线OB与直线CA的交点，点E是直线CP与y轴的交点，若∠ACE=∠AEC，PD=2OD，则PA∶PC=_______.

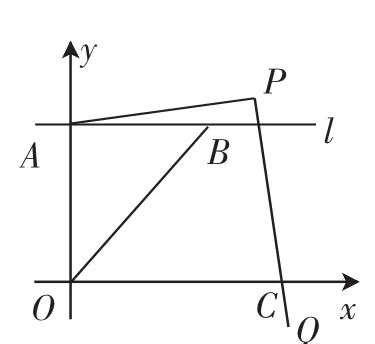
图1

二、苦苦探索

解这题整整用了25分钟，首先遇到的是审题上的困难，题目中有条件“动点P在直线OB上运动”，而题目配的图形中“动点P不在直线OB上”，是提供的图没有用，还是另有玄机？再三读题，确信我们必须重新画图，如何画出大致准确的示意图是我遇到的又一难关.做题积累的经验告诉我准确的几何图形能提供几何直观，发现几何关系，有利于观察、分析、探索思路，专家说“先有直觉感知，后有逻辑推理！”但画出满足题目条件的准确图并非一件顺其自然的事，难度很大.因为经过原点的直线有无数条，因此直线OB的位置没法确定，从而点P的位置也难以确定，动中取静，先大体估一个位置，按要求画出直线OB、在直线OB上取点P，连AP，画出∠APQ=90°，交X轴于点C，如图2，但这样的图形难以满足条件“直线CP与y轴交于点E，且∠ACE=∠AEC”，因此调整画图顺序，分析条件“∠APQ=90°、∠ACE=∠AEC”，这实质上告诉我们AP垂直平分线段CE，因此理顺题目的语句，先画直线CE交x轴于点C，交y轴于点E，再作线段CE的垂直平分线交y轴于点A，再过点A画直线l平行于x轴（其实直线l是一条无用的直线，点B也是无用的点，读到此我们必须排除这些干扰因素），连AC、OP交于点D，画出图3，满足题目条件的图形大致画出了（问题是不一定正好满足最后的条件PD=2OD，这是后面改编试题的思维起点）.图有了，解题的思路也出来了，由于点P是Rt△COE的斜边CE的中点，由中点联想中线的有关性质，因此取OC边的中点M，连PM交AC于点F，则线段PM是Rt△COE的中位线，所以，且PM∥OE.根据平行线分线段成比例定理，F也是线段AC的中点，所以FM是△COA的中位线.设FM=x，则AO=2x.由PM∥OB，得△OAD∽△PFD.由于PD=2OD，所以PF=2AO=4x.又PF是△CAE的中位线，所以AE=2PF=8x.由于∠ACE=∠AEC，所以AC=AE=8x.

图2

图3

在Rt△COA中，AO=2x，AC=8x，根据勾股定理得：

图4

由于题目条件是动点P在直线OB上运动，因此还要考虑点P在线段OB的反向延长线上.类比思考分析，同样的困难仍然是“图”，横仿第一种情况画出草图，如图4所示.由于点P是Rt△COE的斜边CE的中点，因此取OC边的中点M，连PM交AC于点F，则线段PM是 Rt△COE的中位线，所以，且PM∥OE.根据平行线分线段成比例定理，F也是线段AC的中点，所以有FM是△COA的中位线.设FM=x，则AO=2x.由PM∥OE，得△OAD∽△PFD.由于PD=2OD，所以PF=2AO=4x，PF又是△CAE的中位线，所以AE=2PF=8x.由于∠ACE=∠AEC，所以AC=AE=8x.

在Rt△COA中，AO=2x，AC=8x.

三、两点思考

中考说明在老师心目中占据极其重要的地位，大市的中考说明是指导全市中考复习的纲要，老师必然会认真研究学习中考说明，了解中考命题的指导思想，掌握中考复习的考试范围与能力要求，研究中考说明提供的综合训练，掌握考试的形式及试卷结构，根据研究中考说明的心得体会制订中考复习的目标方向，指导中考复习.综合训练三的第16题是填空压轴题，试题来源于何处？考查目标是什么？对我们复习教学有什么启示？

1.命题切勿“拿来主义”.

本题在求解时好象没有用到条件“直线l平行于x轴”和“第一象限内的点B在l上”，为什么会出现这种情况呢？是我解错了，还是题目条件多余？审查我的解答过程，步步有理有据，看看书后提供的答案：“或”，也没有错，因此我想条件“直线l平行于x轴”和“第一象限内的点B在l上”是多余的，放在此处会干扰学生的思维.我尝试进凤凰数学网02号VIP群交流，浙江绍兴郦兴江老师告诉我“这是他们浙江省绍兴市2014年中考卷解答压轴题的最后一问，命题老师如此设计题目配图，意在加大对学生动态图形作图能力的考查，优秀学生不化上一定的解答时间是得不出准确答案的.”郦老师提供原题如下：

如图1，在平面直角坐标系中，直线l平行于x轴，交y轴于点A，第一象限内的点B在l上，连接OB，动点P满足∠APQ=90°，PQ交x轴于点C.

（1）当动点P与点B重合时，若点B的坐标是（2，1），求PA的长.

（2）当动点P在线段OB的延长线上时，若点A的纵坐标与点B的横坐标相等，求PA∶PC的值.

（3）当动点P在直线OB上时，点D是直线OB与直线CA的交点，点E是直线CP与y轴的交点，若∠ACE=∠AEC，PD=2OD，求PA∶PC的值.

原来我市中考说明上的这道填空题直接截取绍兴市2014年中考题的第三问而得，图是直接复制粘贴的.绍兴的压轴大题有第（1）和（2）问铺路，多少给解题者（学生、教师）指明点方向，在辅助线及构图上也有一定的铺垫，包括审题、理解题意.直接截取其最后一问，图也直接复制粘贴，用来作填空压轴题，难度就放大了，等于你要学生上二楼，但抽掉了楼梯，看看学生上楼的非凡本领.解题时单把符合题意的图形作出来就会把让解题者搞晕，而现在的学生，画图能力普遍较差，（现在的作业用的是印刷精美的书，不用抄题，不用画图，最多就是在图上作作辅助线而已，老师普遍不重视或不需要学生抄题），因此不少地市这几年也加大对学生的动态作图能力的考查力度，这可以理解.但命题老师希望不出现满分（或说希望有高分的学生涌现出来，但不希望出现大量的满分学生来）也可以理解，但不考虑学生的实际，任意加大难度，命题直接采用拿来主义，想通过此题抑制99%的人得分，基于这样的目的，就不能理解了.另外，命题直接采用拿来主义也有失公平.考卷中所谓的难题能不能拉开差距，要看命题人的水平，最好的难题应该既不要是超级难题，又不要是陈题，要有思维含量，更要有一定的灵活性，有一定的探究梯度，这样的考题可能才会真正考出学生的思维层次，能够拉开差距，考试时才有区分度.像这样的题目，应当给出示意图，因为题目的本意是考查分类思想、思维的严谨性，以及如何运用其解决比值问题，因此不必在示意图上再去“刁难”“学生”.

2.改编推进发展.

这是一道改编的伪坐标系题，它是先平面几何思构，再放在平面直坐标系中定相关位置，题目好像赋予动态变化背景而成命题，其实没有动态变化.我结合自己做这道绍兴市2014年中考压轴题的思考，也尝试以此题为母题改编几题：

（1）试题改编.

题1：如图5，在Rt△ABC中，D是斜边AB的中点，DE⊥AB交直角边BC于E，连AE、CD交于点G，若DG=2CG，∠CDE= α，则cosα=_______.

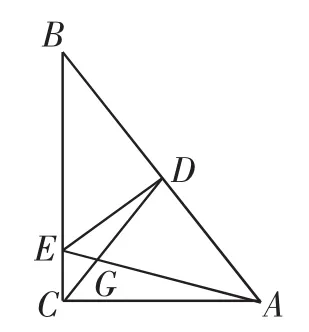
图5

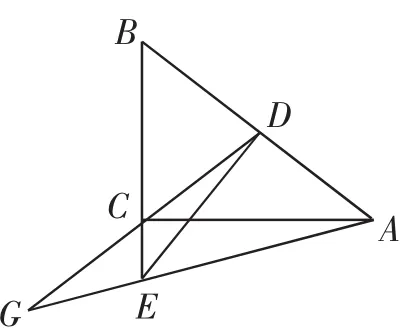
图6

题2：如图6，在Rt△ABC中，D是斜边AB的中点，DE⊥ AB交直角边BC的延长线于E，直线AE、CD交于点G，若DG=2CG，∠CDE=α，则tanα=_______.

题3：在Rt△ABC中，D是斜边AB的中点，DE⊥AB交直角边BC所在直线于E，设直线AE、CD交于点G，若DG= 2CG，则tan∠BAE=_______.

题4：如图7，在Rt△ABC中，D是斜边AB的中点，DE⊥AB交直角边BC于E，连AE、CD交于点G.

①若DG=CG，求∠CDE的度数；②若DG=2CG，求sin∠CDE的值；③若DG=nCG，则sin∠CDE的值是_______.

（2）改编意图说明.

改编试题1、2，直奔主题，为学生画好图形，考查学生的几何推理能力，学生运用所学的三角形的中位线、勾股定理、锐角三角函数、圆等知识，尝试作出一条辅助线解决.改编试题3实质上是本文话题起因中的原题，但语言叙述简洁，学生没有阅读障碍，题目没有提供图形和条件中的“直线”都指明学生要分类讨论问题.改编试题4，条件从“DG=CG”到“DG=nCG”，由特殊到一般，体验课题探究的条件.以这样的方式给出的改编题目，叙述简洁，同时在示意图的帮助下，理解上没有任何困难.下面只要“专心致志”研究如何解答.

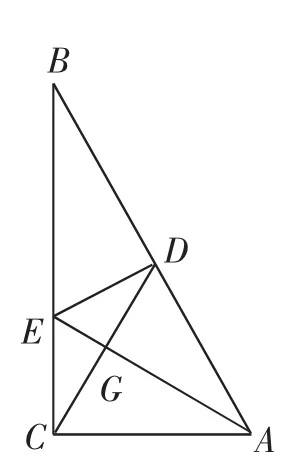
图7

其实改编试题，如何取材选题，如何添加、生成，如何整合、创新，如何为学生设计思维台阶，如何体现新课改理念下考核的评价功能、导向功能及选拔功能，都值得思考.改编试题必须在对原题深入研究的基础上进行问题的重新整合或创新，改编试题必须要利于学生的发展，老师要多做做题，多思考思考题的来源、本质，尝试改编题.

（3）改编试题答案.

题1：

题2：

题3：或

题4：①∠CDE=30°.

②sin∠CDE= .

③sin∠CDE=.