一题多解再深入，多解归一想关联——以平面几何解题教学为例

☉重庆丰都第二中学校 陈晓东

一题多解再深入，多解归一想关联
——以平面几何解题教学为例

☉重庆丰都第二中学校 陈晓东

平面几何的解题教学常常是教研难点，学生学得难，教师教得也不轻松，特别是一些较为复杂的几何题，需要添加恰当的辅助线，才能实现问题的解决.具体到解题教学时，往往这条辅助线是“空中飞来”“显然可作”之类，让本来不会的学生茫然无所适从.本文整理近期教学过程中收集的一些典型几何题例，对比不同辅助线，并跟进教学思考，供分享.

一、例题及思路突破

考题1：如图1，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是弧AB上一点，将扇形AOB沿EF对折，使得折叠后的圆弧A′F恰好与半径OB相切于点G，若OE=4，求点O到折痕EF的距离.

图1

图2

思路突破：如图2所示，作出点O关于折痕EF的对称点O′，则点O′即为折叠后的圆弧A′F的圆心.连接O′G，由圆弧A′F恰好与半径OB相切于点G，得O′G⊥OB于点G.由题意知O′G∥AO.接着可得△O′OG∽△OEH.可设OH= x，则OO′=2x.OE=4，O′G=OA=6.由△O′OG∽△OEH，得比例式，即，化简得x2=12，解得（负值舍去），问题得解.

另解思考：如图3，作出点O关于折痕EF的对称点O′，则点O′即为折叠后的圆弧A′F的圆心.

类似上面的探究知O′G∥AO，O′G=OA=6，连接O′A，容易证明四边形OAO′G为矩形，则△O′AE为直角三角形.由O、O′两点关于折痕EF对称，容易想到连接EO′，则EO′=EO=4.

图3

回顾反思：另解思考巧妙发现了图形中蕴含的特殊性，即O′G∥AO且O′G=AO，从而联想到连接O′A后得到矩形OAO′G，再利用翻折问题中的边不变性，联想到连接EO′，进而确认特殊直角三角形O′AE.

变式追问：求折痕EF的长.

思路简述：如图4，在Rt△OHE中，可求出EH=2；在Rt△OHF中，可求出.从而折痕EF=EH+FH=

图4

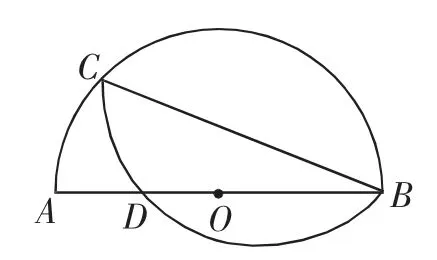
图5

考题2：以半圆中的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D，AD∶BD=1∶3，AB=8，求BC的长.

思路简述：如图6，延长AC、BD′交于A′，连接CD′，根据对称性先确认A′C=AC，A′D′=AD，再利用△A′CD′∽△A′BA，可得乘积式A′D′·A′B=A′C·A′A.设AC= x，则2x2=16，解得.再在Rt△ABC中利用勾股定理求得

图6

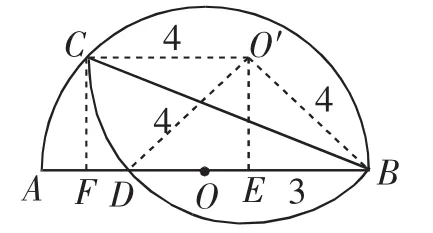
图7

另解思考：想清另一段弧BDC所在圆心O′，构造图7分析，连接O′E、O′C、O′B、O′D，作O′E⊥AB于E，作CF⊥AB于F.在等腰△O′BD中，BE=3，进一步在Rt△O′BE中，确定O′E的长为，于是CF与O′E的长也为，CO与EF的长为4，于是BF=7.最后在Rt△BCF中，可得

考题3：定义：有两条边之比为1∶2的直角三角形叫作潜力三角形.

如图8，△ABC中，∠ABC=90°，D为AB边的中点，E为CD的中点，DF∥AE.

（1）设“潜力三角形”较短直角边为a，斜边长为c，请直接写出c的值；a

图8

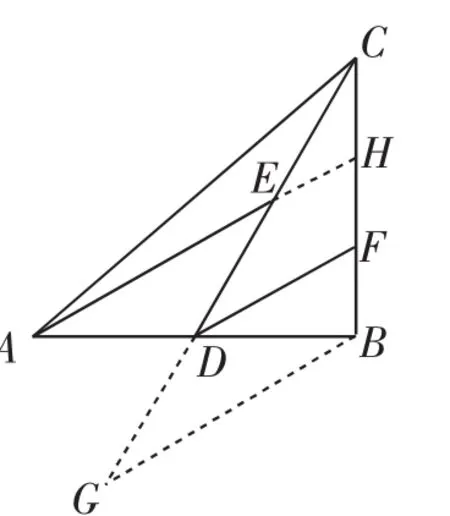
图9

（2）当∠EDF=∠DCF时，求证△BDF是潜力三角形；

（3）若△BDF是潜力三角形，BF=1，求AC的长.

思路突破：如图9，着眼于D为中点且DF∥AE这个双重信息的启示，添加恰当辅助线，作EH∥DF交BC于H点，根据相似及三角形中位线性质容易确定H、F为边BC的三等分点，再由DF=CF，所以△BDF中，DF=2BF，问题获得解决.

回顾反思：在图9中，还可过B作BG∥FD交CD的延长线于G点，可以确定D、E为线段CG的三等分点，从而看出该题的深层结构，感受到不同方法都能解决问题.

考题4：如图10，在矩形ABCD中，E、F分别为AB、CD上两点，且∠EBF=∠DEF=45°，试用等式表示AE、EF、CF三者之间的数量关系，并予以证明.

图10

图11

图12

思路突破：如图11，延长BA、BC交直线EF于G、H，可确认△BGH是等腰直角三角形，再将△BEG绕点B旋转90°到△BG′H的位置，再证出△BG′F≌△BEF，从而把GE、EF、FH集中到△FG′H中，而该三角形是直角三角形（引导学生注意说清∠G′HB、∠FHB都是45°）.这样根据勾股定理得GE2+FH2=EF2，再转化为2AE2+2FC2=EF2.

结构反思：如图12，补成一个大的正方形BHKG后，容易确认两个经典的性质，一是MN=GM+HN，二是GE2+ FH2=EF2，或者2AE2+2FC2=EF2.

二、教学思考

1.教师备课需要追求一题多解，并深入思考“一题何以多解”.

对于一些经典考题，教师拟选用例题重点讲评时，就需要深入思考该题的不同解法，并比较不同解法之间的关系，特别是教师本人要深入思考：一题何以多解？这些多解之间的关联何在？不同思路的辅助线是基于什么想法得到的？是基于哪一种基本图形？（如考题4的结构是一个正方形中的两个经典结构，如图12所示）是基于哪一个数学定理的基本图形发展而来？是否体现了从标准图形向非标准图形的变式？教师备课前多思考上述问题，则解题教学就有了深度，从就题讲题追求一题多得、讲一题会一类的高效课堂.

2.不同解法需要经过优选，并引导学生思考“殊途何以同归”.

备课时教师可能会对同一道习题获得多样化的解法，但并不代表这些解法都要进入课堂，因为有些经典问题的不同解法可能多达10种，而且有些解法本质上大同小异，无须在宝贵的课堂上一一展示，这时教师在备课时需要优选不同解法，挑选一些典型解法，并引导学生深入思考这些不同的解法“殊途何以同归”.比如考题1，不仅可以引导学生对比不同解法，而且还可以成果扩大，给出变式追问，让学生继续求解；再如考题2的两种思路，不同的平行线添加都能实现问题的解决，然而将这两种辅助线都添加在同一图形（如图9）中时，学生就能发现一个平行线等分线段定理的基本图形，这也是引导学生“回到概念去解题”.

3.追求最少的条件及最简的证明，并引导思辨解法的繁简.

我国数学家中科院李大潜院士曾指出：“数学上追求最有用（广泛）的结论、最少的条件（代价）及最简洁的证明，通过严格的数学训练，会逐步形成精益求精、力求尽善尽美的习惯和风格.”面对一些典型问题的求解，我们也要引导学生有这样的追求.常常看到不少学生面对习题讲评时，只是满足于答案的获得，不能深入思考不同解法，特别是对不同解法之间的关系缺少深入的思辨，比较它们的繁简，这时要通过一题多解、解后回顾，训练学生的求简思维，促进他们形成尽善尽美的习惯和风格.想来，这也是数学育人的追求吧.

1.王海燕.删繁就简凸显本质，退回原点推导公式——以一道坐标系中旋转难题为例［J］.中学数学（下），2017（3）.

2.贺清伦.解题研究再深入：以一道习题网络研讨为例［J］.中学数学（下），2017（3）.

3.王成.同类链接促进感悟，模考讲评提升效益——以一次模考题的链接讲评为例［J］.中学数学（下），2017（2）.

4.金弘鑫.解后反思看清结构，变式改编成果扩大——以一道八年级期末模考题为例［J］.中学数学（下），2017（1）.